Общие принципы моделирования и оптимизации электросталеплавильного процесса

Введение

В настоящее время Федеральные программы технического развития металлургии предусматривают дальнейшее увеличение объемов и совершенствование процессов выплавки стали за счет внедрения различных прогрессивных ресурсо- и энергосберегающих технологий. Одной из главных задач современного сталеплавильного производства остается получение расплавленного металлического полупродукта с заданными химическим составом и температурой при минимальных затратах материальных и энергетических ресурсов [1 ‒ 5]. Основные и наиболее универсальные управляющие воздействия, которые влияют на ход и технико-экономические показатели процесса, как правило, неразрывно связаны с оптимизацией параметров технологии [6 ‒ 8]. При этом возникает необходимость реализации задач по обеспечению режимов оптимального функционирования дуговых сталеплавильных печей и решения задач прогнозирования основных показателей электроплавки [5 – 8].

Для решения поставленных задач целесообразны использование ресурсов математического моделирования и разработка инструментальной системы для расчета статических режимов процесса, то есть расчета и анализа процесса на уровне входных-выходных потоков [9 – 12].

Методики расчета статических режимов позволяют решать следующие задачи: расчеты материального и теплового балансов процесса¹ [13 – 15]; оценка предельных энергетических возможностей; определение термодинамических границ существования и условий взаимодействия компонентов в металлургическом агрегате; выбор наиболее эффективных компонентов входного потока с целью получения металла с заданными свойствами для достижении оптимальных технико-экономических показателей [13 – 16].

Методы исследования

При создании статической модели расчета электросталеплавильный процесс рассматривали как сложную термодинамическую систему, в которую поступают конденсированные и газообразные входные среды, а конечными продуктами являются металл, шлак и газ [17 – 20]. В составе конденсированных входных потоков, в зависимости от варианта технологии, присутствуют: металлошихта (жидкий или чушковый чугун, металлический лом); твердые окислители (агломерат, железная руда, окатыши); шлакообразующие материалы (известь, известняк, плавиковый шпат); науглероживатели (металлургический кокс, коксовый орешек, пыль установок сухого тушения кокса (УСТК), электродный бой и т. д.); ферросплавы. Газообразными входными потоками являются кислород и природный газ [21 – 23].

Тогда определяющими параметрами входных потоков будут: K – общее количество; K^f, K^г и \(G_k^f\), \(G_k^{\rm{г}}\) – количество и масса конденсированных, газообразных потоков (индексы f и г соответствуют конденсированным и газообразным потокам); \(N_k^f\), \(N_k^{\rm{г}}\) – количество веществ в k-ом потоке; \(t_k^f\), \(t_k^{\rm{г}}\) и \(\rho _k^f\), \(\rho _k^{\rm{г}}\) – температура и плотность потоков, °С и кг/м³; |R_m|_k, {R_m}_k – содержание вещества R_m в k-ом потоке, %.

Выходные потоки характеризуют параметры: G_м, G_шл, G_г – масса металла, шлака, газа; t_м, t_шл, t_г – температура металла, шлака, газа, °С; N_м, N_шл, N_г – количество веществ в соответствующих фазах; [R_n], (R_n), {R_n} – содержание вещества R_n в металлической, шлаковой и газовой фазах.

При рассмотрении параметров системы приняли, что вещества R_m и R_n являются элементами множества \(\Re \) и могут присутствовать в разных фазах в виде различных соединений E_ixE_jy, состоящих из элементов E_i и E_j множества x. С входными потоками в реактор могут поступать следующие соединения: конденсированная фаза ‒ Fe, C, Mn, Si, S, P, Al, Ni, Mo, W, V, Ti, Cr, B, Cu, FeO, Fe₂O₃, Al₂O₃, CaO, SiO₂, MgO, MnO, P₂O₅, CaS, CaF₂, NiO, V₂O₅, Cr₂O₃, TiO₂, MoO₂, WO₂, CuO, B₂O₃; газовая фаза – H₂O, CO₂, O₂, CH₄, CO, N₂, H₂. Элементами, образующими эти вещества, являются: Fe, C, O, Mn, Si, S, P, Al, Ca, Mg, H, F, Ni, Ti, V, Cr, N, B, Cu, Mo, W.

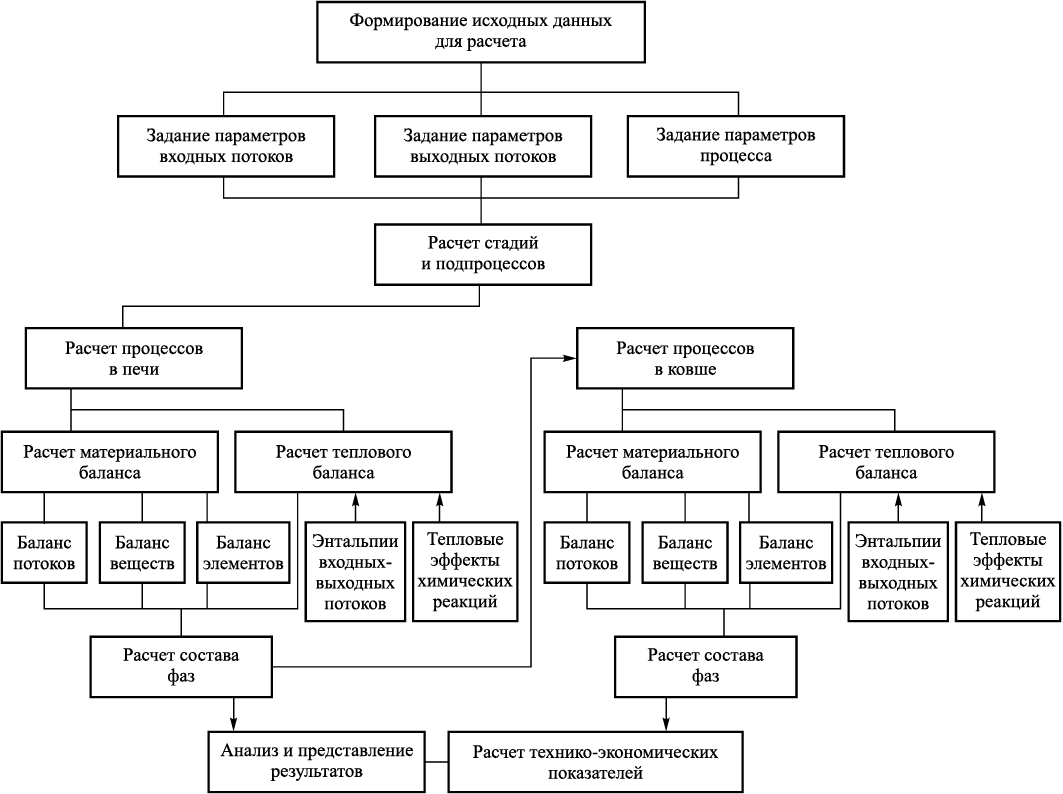
Расчет статических режимов электросталеплавильного процесса заключается в определении расходов шихтовых материалов, необходимых для достижения заданных параметров и температуры металла, и базируется на балансовых моделях и уравнениях термодинамики. Схема расчета представлена на рис. 1.

Задание исходных данных предусматривает ввод следующей информации: задание параметров входных потоков; задание параметров процесса; задание коэффициентов распределения элементов по фазам.

В качестве параметров процесса приняты: t_м, t_шл, t_г – температура фаз, °С, Q_пот ‒ тепловые потери в окружающую среду, Q_кор – потери металла с корольками; η_CO – степень окисления углерода до СО; η_FeO – степень окисления железа до FeO; α – степень усвоения кислорода.

Коэффициенты распределения элементов по фазам заданы с учетом экспериментальных данных в заданных диапазонах изменения параметров входных-выходных потоков.

В качестве технико-экономических показателей приняты: Э – энергоемкость процесса, кВт·ч/т; С – себестоимость продукции, руб./т; П – производительность агрегата, т/ч; g_k – удельные расходы материалов, кг/т.

После задания необходимых для расчета параметров формируется таблица исходных данных по входным потокам. В качестве исходной информации используются: температура, плотность и расход k-го входного потока. Ввод исходных данных предусматривает задание химического состава шихтовых материалов. Для всех вариантов расчетов приведен базовый состав конденсированных и газообразных входных потоков, а также летучих компонентов шихты, который при желании может быть изменен пользователем.

Результаты и их обсуждение

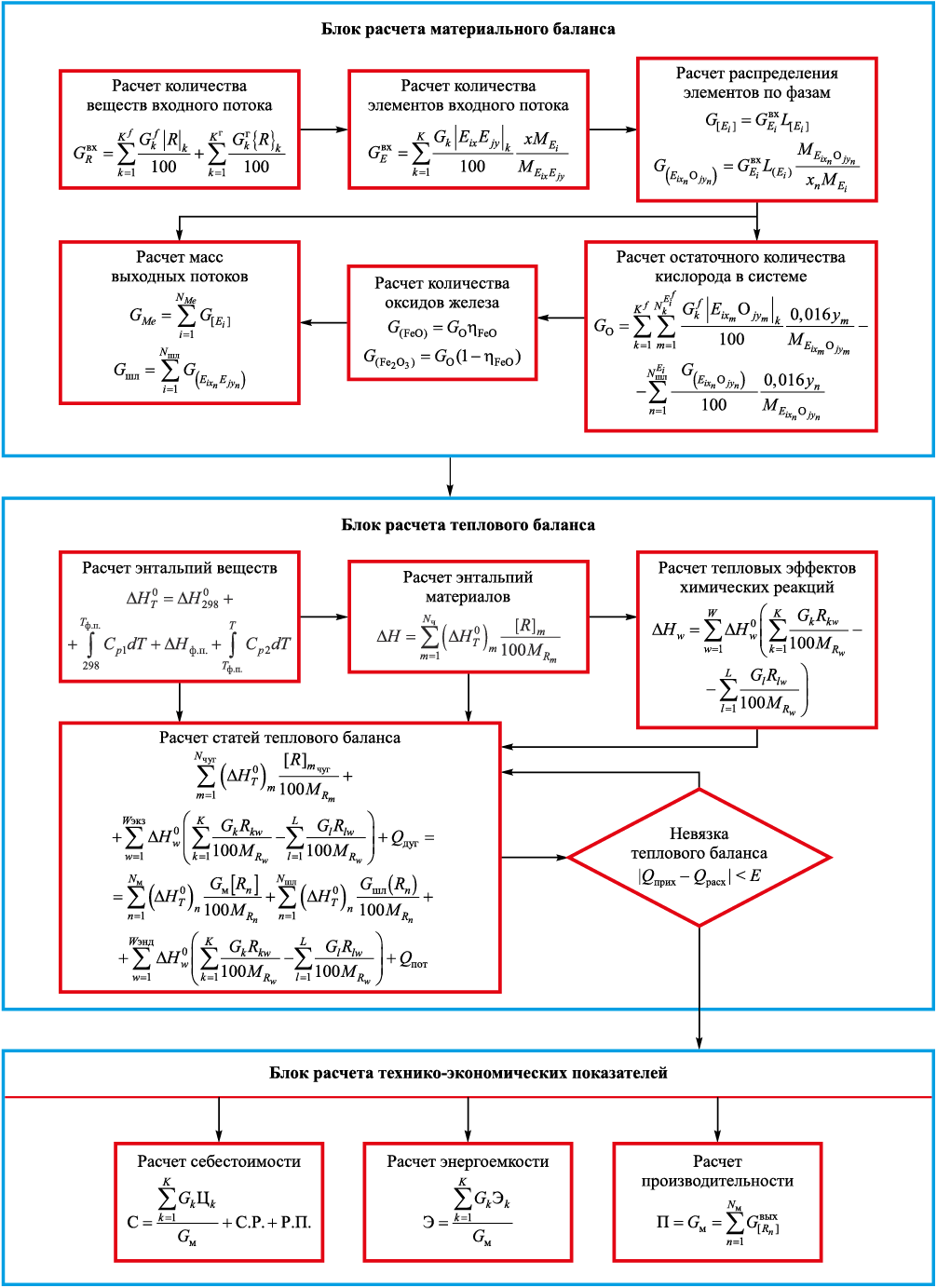
Расчет статических режимов электросталеплавильного процесса осуществляется на основе материального и теплового балансов, базирующихся на законах сохранения массы и энергии относительно составляющих гетерогенной системы. Алгоритм расчета материального и теплового балансов представлен на рис. 2.

Материальный баланс для всей системы на уровне входных-выходных потоков имеет вид:

\[\sum\limits_{k = 1}^K {{G_k}}  = \sum\limits_{l = 1}^L {{G_l}} .\]

С учетом фаз уравнение материального баланса можно представить следующим образом:

\[\sum\limits_{k = 1}^{{K^f}} {G_k^f}  + \sum\limits_{k = 1}^{{K^{\rm{г}}}} {G_k^{\rm{г}}}  = {G_{\rm{м}}} + {G_{{\rm{шл}}}} + {G_{\rm{г}}}.\]

Общая масса веществ, поступающих в печь с входными потоками, соcтавляет:

\[\sum\limits_{k = 1}^K {{G_k}}  = \sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^f} {\frac{{G_k^f{{\left| {{R_m}} \right|}_k}}}{{100}} + } } \sum\limits_{k = 1}^{{K^{\rm{г}}}} {\sum\limits_{m = 1}^{N_k^{\rm{г}}} {\frac{{G_k^{\rm{г}}{{\{ {R_m}\} }_k}}}{{100}}} } .\]

Масса веществ выходных потоков определяется массой веществ в металлической, шлаковой и газовой фазах:

\[\sum\limits_{l = 1}^L {{G_l}}  = \sum\limits_{n = 1}^{{N_{\rm{м}}}} {\frac{{{G_{\rm{м}}}\left[ {{R_n}} \right]}}{{100}} + } \sum\limits_{n = 1}^{{N_{{\rm{шл}}}}} {\frac{{{G_{{\rm{шл}}}}\left( {{R_n}} \right)}}{{100}} + } \sum\limits_{n = 1}^{{N_{\rm{г}}}} {\frac{{{G_{\rm{г}}}\left\{ {{R_n}} \right\}}}{{100}}} .\]

Таким образом, уравнение материального баланса на уровне потоков веществ имеет следующий вид:

\[\begin{array}{c}\sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^f} {\frac{{G_k^f{{\left| {{R_m}} \right|}_k}}}{{100}} + } } \sum\limits_{k = 1}^{{K^{\rm{г}}}} {\sum\limits_{m = 1}^{N_k^{\rm{г}}} {\frac{{G_k^{\rm{г}}{{\{ {R_m}\} }_k}}}{{100}}} }  = \\ = \sum\limits_{n = 1}^{{N_{\rm{м}}}} {\frac{{{G_{\rm{м}}}\left[ {{R_n}} \right]}}{{100}} + } \sum\limits_{n = 1}^{{N_{{\rm{шл}}}}} {\frac{{{G_{{\rm{шл}}}}\left( {{R_n}} \right)}}{{100}} + } \sum\limits_{n = 1}^{{N_{\rm{г}}}} {\frac{{{G_{\rm{г}}}\left\{ {{R_n}} \right\}}}{{100}}} .\end{array}\]

Для того, чтобы определить состав фаз выходных потоков, составляются уравнения баланса по каждому элементу Е_i, который может присутствовать в разных фазах в виде различных соединений:

\[\begin{array}{c}\sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^{E_i^f}} {\frac{{G_k^f{{\left| {{E_{i{x_m}}}{E_{j{y_m}}}} \right|}_k}}}{{100}}} \frac{{{x_m}{M_{{E_i}}}}}{{{M_{{E_{i{x_m}}}{E_{j{y_m}}}}}}}}  + \\ + \sum\limits_{k = 1}^{{K^{\rm{г}}}} {\sum\limits_{m = 1}^{N_k^{E_i^{\rm{г}}}} {\frac{{G_k^{\rm{}}{{\left\{ {{E_{i{x_m}}}{E_{j{y_m}}}} \right\}}_k}}}{{100}}} \frac{{{x_m}{M_{{E_i}}}}}{{{M_{{E_{i{x_m}}}{E_{j{y_m}}}}}}}}  = \\ = \frac{{{G_{\rm{м}}}[{E_i}]}}{{100}} + \sum\limits_{n = 1}^{N_{{\rm{шл}}}^{{_i}}} {\frac{{{G_{{\rm{шл}}}}\left( {{E_{i{x_n}}}{E_{j{y_n}}}} \right)}}{{100}}} \frac{{{x_n}{M_{{E_i}}}}}{{{M_{{E_{i{x_n}}}{E_{j{y_n}}}}}}} + \\ + \sum\limits_{n = 1}^{N_{\rm{г}}^{{E_i}}} {\frac{{{G_{\rm{г}}}\left\{ {{E_{i{x_n}}}{E_{j{y_n}}}} \right\}}}{{100}}} \frac{{{x_n}{M_{{E_i}}}}}{{{M_{{E_{i{x_n}}}{E_{j{y_n}}}}}}},\end{array}\]

где \(\left| {{E_{i{x_m}}}{E_{j{y_m}}}_k} \right|\), \(\left\{ {{E_{i{x_m}}}{E_{j{y_m}}}} \right\}\) ‒ концентрация m-го вещества, содержащего элемент Е_i в k-ом конденсированном или газообразном входном потоке соответственно, %; [E_i] ‒ концентрация вещества, состоящего из элемента Е_i, в металле, %; \(\left( {{E_{i{x_n}}}{E_{j{y_n}}}} \right)\), \(\left\{ {{E_{i{x_n}}}{E_{j{y_n}}}} \right\}\) – концентрация n-го вещества, содержащего элемент Е_i в шлаковой и газовой фазах выходного потока соответственно, %; \(N_k^{E_i^f}\),  \(N_{{\rm{шл}}}^{{E_i}}\), \(N_{\rm{г}}^{{E_i}}\) – количество веществ, содержащих элемент Е_i, в k-ом входном потоке, шлаке и газе; х_m, y_m – стехиометрические коэффициенты m-го соединения элемента Е_i;  \({M_{{E_i}}}\), \({M_{{E_{i{x_m}}}{E_{j{y_m}}}}}\) – молярные массы Е_i элемента и его соединений, кг/моль.

Общая масса конденсированного вещества R, поступающего в систему с входными потоками, составляет:

\[G_{\left| R \right|}^{{\rm{вх}}} = \sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^f} {\frac{{G_k^f\left| {{R_m}_k} \right|}}{{100}}} } .\]

Масса газообразного вещества R, поступающего в систему с входными потоками, также определяется с учетом его содержания в газообразных входных потоках:

\[G_{\{ R\} }^{{\rm{вх}}} = \sum\limits_{k = 1}^{{K^{\rm{г}}}} {\sum\limits_{m = 1}^{N_k^{\rm{г}}} {\frac{{G_k^{\rm{г}}{{\{ {R_m}\} }_k}}}{{100}}} } .\]

Состав фаз выходного потока определяется следующим образом. В соответствии с коэффициентами распределения элементов между фазами количество элемента Е_i в металле определяется по формуле:

\[{G_{\left[ {{E_i}} \right]}} = G_{^{{_{ii}}}}^{{\rm{вх}}}{L_{[{E_i}]}},\]

здесь \({L_{[{E_i}]}}\) – коэффициент распределения элемента E_i в металле.

Количество оксида элемента Е_i в шлаке соответственно составляет

\[{G_{\left( {{E_{i{x_n}}}{{\rm{O}}_{j{y_n}}}} \right)}} = G_{{E_i}}^{{\rm{вх}}}{L_{\left( {{E_i}} \right)}}\frac{{{M_{{E_{i{x_n}}}{{\rm{O}}_{j{y_n}}}}}}}{{{x_n}{M_{{E_i}}}}}.\]

Определяем количество кислорода, которое остается в системе после окисления всех компонентов и затрачивается на окисление железа:

\[\begin{array}{c}{G_{\rm{O}}} = \sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^{E_i^f}} {\frac{{G_k^f{{\left| {{E_{i{x_m}}}{{\rm{O}}_{{y_m}}}} \right|}_k}}}{{100}}} \frac{{0,016{y_m}}}{{{M_{{E_{i{x_m}}}{{\rm{O}}_{j{y_m}}}}}}}}  - \\ - \sum\limits_{n = 1}^{N_{{\rm{шл}}}^{{_i}}} {\frac{{{G_{({E_{i{x_n}}}{{\rm{O}}_{j{y_n}}})}}}}{{100}}} \frac{{0,016{y_n}}}{{{M_{{E_{i{x_n}}}{{\rm{O}}_{j{y_n}}}}}}}.\end{array}\]

Определяем количество оксидов железа в шлаке:

\[\begin{array}{c}{G_{({\rm{FeO}})}} = G{}_{\rm{O}}{\eta _{{\rm{FeO}}}};\\{G_{({\rm{F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}})}} = G{}_{\rm{O}}(1 - {\eta _{{\rm{FeO}}}}).\end{array}\]

Тогда количество железа в металле определим следующим образом:

\[{G_{[{\rm{Fe}}]}} = G_{{\rm{Fe}}}^{{\rm{вх}}} - {G_{({\rm{FeO}})}}\frac{{0,056}}{{0,072}} - G_{{\rm{F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}^{{\rm{вх}}}\frac{{0,112}}{{0,160}}.\]

Соответственно массы металла и шлака будут составлять:

\[\begin{array}{c}{G_{Me}} = \sum\limits_{i = 1}^{{N_{Me}}} {{G_{[{E_i}]}}} ;\\{G_{{\rm{шл}}}} = \sum\limits_{i = 1}^{{N_{{\rm{шл}}}}} {{G_{({E_i}_{_{xn}}{E_{{i_{yn}}}})}}} .\end{array}\]

Аналогично проводится расчет состава и массы фаз в ковше, только в данном случае входными потоками являются металл, полученный в печи, и шлак, частично попадающий в ковш при сливе.

Для расчета состава компонентов газовой фазы предложен следующий механизм образования отходящих газов в электропечи. В технологии с применением природного газа сделано допущение его полного сгорания, что приводит к химическому составу газов в выходном потоке при классическом разложении.

При полном сгорании природного газа образуются СО₂ и Н₂О:

\[\begin{array}{l}G_{\{ {\rm{C}}{{\rm{O}}_2}\} }^{{\rm{}}} = G_{\{ {\rm{C}}{{\rm{H}}_4}\} }^{{\rm{}}}\left( {1 - {\eta _{{\rm{}}}}} \right)\frac{{0,044}}{{0,016}};\\G_{\{ {{\rm{H}}_2}{\rm{O}}\} }^{{\rm{}}} = G_{\{ {\rm{C}}{{\rm{H}}_4}\} }^{{\rm{}}}\left( {1 - {\eta _{{\rm{}}}}} \right)\frac{{0,018}}{{0,016}}.\end{array}\]

Количество СО, образующегося при горении углерода шихты, можно определить следующим образом:

\[\begin{array}{l}G_{\{ {\rm{C}}{{\rm{O}}_2}\} }^{{\rm{гор}}} = G_{\{ {\rm{C}}{{\rm{H}}_4}\} }^{{\rm{вх}}}\left( {1 - {\eta _{{\rm{конв}}}}} \right)\frac{{0,044}}{{0,016}};\\G_{\{ {{\rm{H}}_2}{\rm{O}}\} }^{{\rm{гор}}} = G_{\{ {\rm{C}}{{\rm{H}}_4}\} }^{{\rm{вх}}}\left( {1 - {\eta _{{\rm{конв}}}}} \right)\frac{{0,018}}{{0,016}}.\end{array}\]

С учетом горения природного газа количество СО₂ в отходящих газах будет составлять:

\[{G_{\{ {\rm{C}}{{\rm{O}}_{\rm{2}}}\} }} = (1 - {{\rm{\eta }}_{{\rm{CO}}}})\left( {\sum\limits_{k = 1}^{{K^f}} {\frac{{G_k^f{{\left|  \right|}_k}}}{{100}} - \frac{{{G_{\rm{м}}}\left[ C \right]}}{{100}}} } \right)\frac{{0,044}}{{0,012}} + G_{{\rm{\{ C}}{{\rm{O}}_{\rm{2}}}{\rm{\} }}}^{{\rm{гор}}}.\]

Общее количество водорода в отходящих газах составляет:

\[{G_{\{ {{\rm{H}}_{\rm{2}}}\} }} = G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{\} }}}^{{\rm{вх}}}.\]

Количество водяных паров определяется как

\[{G_{\{ {{\rm{H}}_{\rm{2}}}{\rm{O}}\} }} = G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{O\} }}}^{{\rm{вх}}} + G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{O\} }}}^{{\rm{гор}}}.\]

Количество азота в отходящих газах равно количеству азота, поступающего с входными потоками в единицу времени:

\[{G_{\{ {{\rm{N}}_{\rm{2}}}\} }} = G_{{\rm{\{ }}{{\rm{N}}_{\rm{2}}}{\rm{\} }}}^{{\rm{вх}}}.\]

Количество SO₂ в отходящих газах определяется в соответствии с коэффициентом перехода серы в газовую фазу:

\[{G_{\{ {\rm{S}}{{\rm{O}}_{\rm{2}}}\} }} = G_{\rm{S}}^{{\rm{вх}}}{{\rm{\alpha }}_{{\rm{\{ S\} }}}}\frac{{0,064}}{{0,032}}.\]

Общая масса газа составляет:

\[{G_{\rm{г}}} = G_{{\rm{\{ CO\} }}}^{{\rm{вых}}} + G_{{\rm{\{ C}}{{\rm{O}}_{\rm{2}}}{\rm{\} }}}^{{\rm{вых}}} + G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{\} }}}^{{\rm{вых}}} + G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{\} }}}^{{\rm{вых}}} + G_{{\rm{\{ S}}{{\rm{O}}_{\rm{2}}}{\rm{\} }}}^{{\rm{вых}}} + G_{{\rm{\{ }}{{\rm{N}}_{\rm{2}}}{\rm{\} }}}^{{\rm{вых}}}.\]

При выводе уравнений теплового баланса принято, что основными определяющими процессами для теплового состояния являются: физическое тепло шихтовых материалов; теплообмен с окружающей средой; тепло от горения электрической дуги; химические реакции с соответствующими тепловыми эффектами. Уравнения теплового баланса строили на основе закона сохранения энергии Q_прих = Q_расх.

С учетом теплосодержания входных-выходных потоков, общего тепла химических реакций, протекающих в системе, тепла дуги, а также теплообмена с окружающей средой уравнение теплового баланса имеет следующий вид:

\[\sum\limits_{k = 1}^{{K^f}} {G_k^f\Delta H_k^f}  + \sum\limits_{k = 1}^{{K^{\rm{г}}}} {G_k^{\rm{}}} \Delta H_k^{\rm{г}} + {Q_{{\rm{дуг}}}} = \sum\limits_{l = 1}^L {{G_l}\Delta {H_l}}  + \Delta {H_{{\rm{х}}{\rm{.}}{\rm{р.}}}} + {Q_{{\rm{пот}}}},\]

где \(\Delta H_k^f\), \(\Delta H_k^{\rm{г}}\), ΔH_l ‒ энтальпии единицы массы k-го конденсированного либо газообразного входного и l-го выходного потоков относительно нормальных условий и температуры 298 К; Q_дуг ‒ приход тепла в систему от горения дуги; Q_пот ‒ тепловые потери в окружающую среду; ΔН_х.р. ‒ суммарный тепловой эффект химических реакций.

Энтальпию, отличную от нуля, имеет только жидкий чугун, тогда энтальпия единицы массы жидкого чугуна относительно T = 298 К будет равна:

\[\Delta {H_{{\rm{чуг}}}} = \sum\limits_{m = 1}^{{N_{{\rm{чуг}}}}} {{{\left( {\Delta H_T^0} \right)}_m}\frac{{{{[R]}_m}_{_{{\rm{чуг}}}}}}{{100{M_{{R_m}}}}}} ,\]

где \({\left( {\Delta H_T^0} \right)_m}\) ‒ изменение энтальпии m-го вещества жидкого чугуна при нагреве от 298 К до T_k, кДж/моль; \({[R]_m}_{_{{\rm{чуг}}}}\) ‒ концентрация вещества R_m, %; \({M_{{R_m}}}\) ‒ молярная масса вещества R_m, кг/моль.

Энтальпии единицы массы металла, шлака и газа соответственно равны:

\[\begin{array}{c}\Delta {H_{\rm{м}}} = \sum\limits_{n = 1}^{{N_{\rm{м}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{[{R_n}]}}{{100{M_{{R_n}}}}}} ;\\\Delta {H_{{\rm{шл}}}} = \sum\limits_{n{\rm{ }} = {\rm{ }}1}^{{N_{{\rm{шл}}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{({R_n})}}{{100{M_{{R_n}}}}}} ;\\\Delta {H_{\rm{г}}} = \sum\limits_{n{\rm{ }} = {\rm{ }}1}^{{N_{\rm{г}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{\{ {R_n}\} }}{{100{M_{{R_n}}}}}} .\end{array}\]

Тепловой эффект химических реакций определяется суммой тепловых эффектов независимых реакций перехода системы из начального состояния в конечное:

\[\Delta {H_{{\rm{х}}{\rm{.}}{\rm{р.}}}} = \sum\limits_{w = 1}^W {\Delta {H_w}} ,\]

где W – число независимых реакций; \(\Delta {H_w} = \Delta H_w^0\Delta {n_{{R_w}}}\) – тепловой эффект w-ой химической реакции, кДж/моль; \(\Delta H_w^0\) ‒ стандартный тепловой эффект w-ой химической реакции; \(\Delta {n_{{R_w}}}\) ‒ количество молей вещества R, прореагировавшего в w-ой реакции.

Число молей участвовавшего в реакции вещества R_w определяется разностью его содержания во входных и выходных потоках:

\[\Delta {n_{{R_w}}} = \sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} .\]

Тепло от горения дуги определяем с учетом расхода электроэнергии:

Q_дуг = 3600E,

где Е – расход электроэнергии, кВт·ч.

С учетом вышеизложенного уравнение теплового баланса имеет следующий вид:

\[\begin{array}{c}\sum\limits_{m = 1}^{{N_{\rm{чуг}}}_{{\rm{чуг}}}} {{{\left( {\Delta H_T^0} \right)}_m}\frac{{{{[R]}_m}_{_{{\rm{}}}}}}{{100{M_{{R_m}}}}}}  + \\ + \sum\limits_{w = 1}^{W{\rm{экз}}} {\Delta H_w^0} \left( {\sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} } \right) + {Q_{{\rm{дуг}}}} = \\ = \sum\limits_{n = 1}^{{N_{\rm{м}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{{G_{\rm{м}}}\left[ {{R_n}} \right]}}{{100{M_{{R_n}}}}} + } \sum\limits_{n = 1}^{{N_{{\rm{шл}}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{{G_{{\rm{шл}}}}\left( {{R_n}} \right)}}{{100{M_{{R_n}}}}} + } \\ + \sum\limits_{w = 1}^{W{\rm{энд}}} {\Delta H_w^0\left( {\sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} } \right)}  + {Q_{{\rm{пот}}}}.\end{array}\]

Основными статьями приходной части теплового баланса являются тепло жидкого чугуна, тепло экзотермических реакций окисления компонентов шихты газообразным кислородом, тепло реакций шлакообразования и тепло горения дуги. К расходной части теплового баланса относятся затраты тепла на нагрев металла, шлака и газа, на разложение карбонатов и оксидов железа, на испарение влаги и тепловые потери в окружающую среду.

Энтальпии входных и выходных потоков рассчитывали с использованием следующих справочных данных: коэффициентов аппроксимационного уравнения для теплоемкости вещества (c₀, c_–1, c₁, c₂, c₃), изменения энтальпии образования и энтропии при стандартной температуре (\({\Delta _f}H_{298}^0\), \(S_{298}^0\)), данных по фазовым переходам (Т_ф.п., \(\Delta H_{{\rm{ф}}{\rm{.}}{\rm{п.}}}^0\)) для индивидуальных веществ.

Решение оптимизационной задачи на основе формальных методов предусматривает выбор различных критериев и задание системы ограничений (требования к составу металла, диапазоны изменения расходов компонентов шихтовых материалов и параметров состояния системы, соблюдение закона сохранения массы на уровне потоков, веществ и элементов; соблюдение закона сохранения энергии).

В качестве критериев могут быть выбраны следующие показатели:

– суммарный расход шихтовых материалов на единицу продукции, кг/т,

\[{\rm{Р}} = \sum\limits_{k = 1}^K {{g_k} = } {\rm{ }}\frac{{\sum\limits_{k = 1}^K {{G_k}} }}{{{G_{\rm{м}}}}} \cdot 1000 \to {\rm{min}};\]

– себестоимость продукции, руб/т,

\[{\rm{C}} = \frac{{\sum\limits_{k = 1}^K {{G_k}{{\rm{Ц}}_k}} }}{{{G_{\rm{м}}}}} + {\rm{O}}{\rm{.P}}{\rm{.}} + {\rm{P}}{\rm{.П}}{\rm{.}} \to {\rm{min}};\]

– энергозатраты на единицу продукции, ГДж/т,

\[{\rm{Э}} = \frac{{\sum\limits_{k = 1}^K {{G_k}{{\rm{Э}}_k}} }}{{{G_{\rm{м}}}}} \to {\rm{min}};\]

– производительность агрегата

\[{\rm{П}} = {G_{\rm{м}}} = \sum\limits_{n = 1}^{{N_{\rm{м}}}} {G_{[{R_n}]}^{{\rm{вых}}}}  \to {\rm{max}}{\rm{,}}\]

где Ц_k – цена k-го материала входных потоков, руб/т; О.Р. – общезаводские затраты, руб./т; Р.П. ‒ расходы по переделу, руб./т; Э_k – удельная энергоемкость k-го материала, ГДж/т.

Постановка задачи оптимизации заключается в нахождении экстремума одного из критериев при выполнении следующих ограничений:

– на диапазоны изменения расходов шихтовых материалов:

G_{k min} < G_k < G_{k max};

– на параметры металла и шлака:

[R_n]_min < [R_n] < [R_n]_max (n = 1 ÷ N_м);

(R_n)_min < (R_n) < (R_n)_max (n = 1 ÷ N_шл);

T_{l min} < T_l < T_{l max} (l = 1 ÷ L);

‒ при соблюдении закона сохранения массы на уровне потоков, веществ и элементов:

\[\begin{array}{c}\sum\limits_{k = 1}^{{K^f}} {G_k^f}  + \sum\limits_{k = 1}^{{K^{\rm{г}}}} {G_k^{\rm{г}}}  = {G_{\rm{м}}} + {G_{{\rm{шл}}}} + {G_{\rm{г}}};\\\sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^f} {\frac{{G_k^f{{\left| {{R_m}} \right|}_k}}}{{100}} + } } \sum\limits_{k = 1}^{{K^{\rm{г}}}} {\sum\limits_{m = 1}^{N_k^{\rm{г}}} {\frac{{G_k^{\rm{г}}{{\{ {R_m}\} }_k}}}{{100}}} }  = \\ = \sum\limits_{n = 1}^{{N_{\rm{м}}}} {\frac{{{G_{\rm{м}}}\left[ {{R_n}} \right]}}{{100}} + } \sum\limits_{n = 1}^{{N_{{\rm{шл}}}}} {\frac{{{G_{{\rm{шл}}}}\left( {{R_n}} \right)}}{{100}} + } \sum\limits_{n = 1}^{{N_{\rm{г}}}} {\frac{{{G_{\rm{г}}}\left\{ {{R_n}} \right\}}}{{100}}} ;\\\sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^{E_i^f}} {\frac{{G_k^f{{\left| {{E_{i{x_m}}}{E_{j{y_m}}}} \right|}_k}}}{{100}}} \frac{{{x_m}{M_{{E_i}}}}}{{{M_{{E_{i{x_m}}}{E_{j{y_m}}}}}}}}  + \\ + \sum\limits_{k = 1}^{{K^{\rm{г}}}} {\sum\limits_{m = 1}^{N_k^{E_i^{\rm{г}}}} {\frac{{G_k^{\rm{г}}{{\left\{ {{E_{i{x_m}}}{E_{j{y_m}}}} \right\}}_k}}}{{100}}} \frac{{{x_m}{M_{{E_i}}}}}{{{M_{{E_{i{x_m}}}{E_{j{y_m}}}}}}}}  = \\ = \frac{{{G_{\rm{м}}}[{E_i}]}}{{100}} + \sum\limits_{n = 1}^{N_{{\rm{шл}}}^{{_i}}} {\frac{{{G_{{\rm{шл}}}}\left( {{E_{i{x_n}}}{E_{j{y_n}}}} \right)}}{{100}}} \frac{{{x_n}{M_{{E_i}}}}}{{{M_{{E_{i{x_n}}}{E_{j{y_n}}}}}}} + \\ + \sum\limits_{n = 1}^{N_{\rm{г}}^{{E_i}}} {\frac{{{G_{\rm{г}}}\left\{ {{E_{i{x_n}}}{E_{j{y_n}}}} \right\}}}{{100}}} \frac{{{x_n}{M_{{E_i}}}}}{{{M_{{E_{i{x_n}}}{E_{j{y_n}}}}}}};\end{array}\]

‒ закона сохранения энергии:

\[\begin{array}{c}\sum\limits_{m = 1}^{{N_{{\rm{чуг}}}}} {{{\left( {\Delta H_T^0} \right)}_m}\frac{{{{[R]}_m}_{_{{\rm{чуг}}}}}}{{100{M_{{R_m}}}}}}  + \\ + \sum\limits_{w = 1}^{W{\rm{экз}}} {\Delta H_w^0} \left( {\sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} } \right) + {Q_{{\rm{дуг}}}} = \\ = \sum\limits_{n = 1}^{{N_{\rm{м}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{{G_{\rm{м}}}\left[ {{R_n}} \right]}}{{100{M_{{R_n}}}}} + } \sum\limits_{n = 1}^{{N_{{\rm{шл}}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{{G_{{\rm{шл}}}}\left( {{R_n}} \right)}}{{100{M_{{R_n}}}}} + } \\ + \sum\limits_{w = 1}^{W{\rm{энд}}} {\Delta H_w^0} \left( {\sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} } \right) + {Q_{{\rm{пот}}}};\end{array}\]

‒ выполнение одного из целевых условий:

P_min < P < P_max;

C_min < C < C_max;

Э_min < Э < Э_max;

П_min < П < П_max.

Таким образом, разработан метод математического моделирования процесса электроплавки и его оптимизации, который включает системное решение взаимосвязанных оптимизационных задач.

Выводы

Выполнен анализ и разработан метод математического моделирования и оптимизации электросталеплавильного процесса, особенностью которого является системное решение комплекса взаимосвязанных оптимизационных задач по определению приемлемых условий протекания процессов в металлургической системе с использованием методов моделирования и оптимизации. Предложены технологические режимы реализации технологии электроплавки.