Общие принципы моделирования и оптимизации электросталеплавильного процесса

Введение

Federal programs for the technological development of metallurgy currently call for further growth in steel output and for continued improvement of steelmaking processes through the adoption of advanced resource- and energy-saving technologies. A central objective of modern steelmaking is to produce a molten metallic semiproduct with a specified chemical composition and temperature while minimizing material and energy consumption [1 ‒ 5]. The most universal control actions affecting both process evolution and its technical and economic indicators are typically inseparable from the optimization of technology parameters [6 ‒ 8]. This, in turn, necessitates solving problems related to establishing optimal operating modes for electric arc furnaces and forecasting the key indicators of electric melting [5 – 8].

Addressing these tasks benefits from mathematical modeling and from developing an instrumental system for calculating the static modes of the process, i.e., for analyzing the process at the level of input–output flows [9 – 12].

Static-mode calculation methods enable, among other things, determination of the material and thermal balances¹ [13 – 15]; evaluation of limiting energy capabilities, identification of thermodynamic feasibility limits and interaction conditions for components within a metallurgical unit, and selection of the most effective components of the input flow to obtain metal with specified properties while achieving optimal technical and economic indicators [13 – 16].

Methods

When developing the static calculation model, the electric steelmaking process was considered as a complex thermodynamic system into which condensed and gaseous input media are supplied, while the final products are metal, slag, and gas [17 ‒ 20]. Depending on the selected technological route, the condensed input flows include: metal charge (liquid or pig iron, steel scrap); solid oxidizers (sinter, iron ore, pellets); slag-forming materials (lime, limestone, fluorspar); carburizers (metallurgical coke, coke breeze, dust from dry coke quenching units, electrode scrap, etc.); and ferroalloys. The gaseous input flows are oxygen and natural gas [21 – 23].

Accordingly, the defining parameters of the input flows are: K – the total number of flows; K^f, K^g and \(G_k^f\), \(G_k^{\rm{g}}\) – the number and mass of condensed and gaseous flows, respectively (the subscripts f and g denote condensed and gaseous flows); \(N_k^f\) and \(N_k^{\rm{g}}\) – the number of substances in the k-th flow; \(t_k^f\), \(t_k^{\rm{g}}\) and \(\rho _k^f\), \(\rho _k^{\rm{g}}\) – the temperature (°C) and density (kg/m³) of the flows; |R_m|_k, {R_m}_k – the content of substance R_m in the k-th flow, %.

The output flows are characterized by the following parameters: G_m, G_sl, G_g – the mass of metal, slag, and gas; t_m, t_sl, t_g – the temperature of metal, slag, and gas, °C; N_m, N_sl, N_g – the number of substances in the corresponding phases; [R_n], (R_n), {R_n} – the content of substance R_n in the metallic, slag, and gas phases, respectively.

In defining the system parameters, it was assumed that substances R_m and R_n are elements of the set \(\Re \) and may be present in different phases in the form of various compounds E_ixE_jy, composed of elements E_i and E_j from the elemental set x. With the input flows, the following compounds may enter the reactor: condensed phase ‒ Fe, C, Mn, Si, S, P, Al, Ni, Mo, W, V, Ti, Cr, B, Cu, FeO, Fe₂O₃, Al₂O₃, CaO, SiO₂, MgO, MnO, P₂O₅, CaS, CaF₂, NiO, V₂O₅, Cr₂O₃, TiO₂, MoO₂, WO₂, CuO, B₂O₃; gaseous phase – H₂O, CO₂, O₂, CH₄, CO, N₂, H₂. The elements forming these substances are: Fe, C, O, Mn, Si, S, P, Al, Ca, Mg, H, F, Ni, Ti, V, Cr, N, B, Cu, Mo, W.

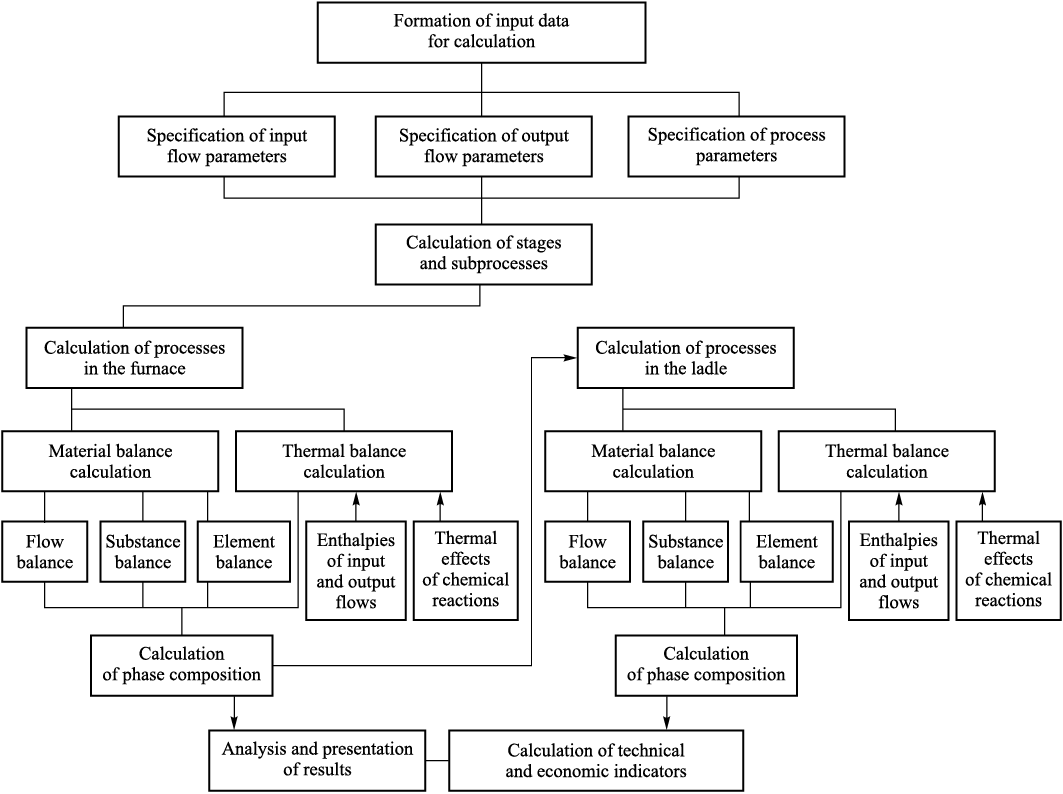
Calculation of the static modes of the electric steelmaking process involves determining the consumption rates of charge materials required to achieve the specified metal parameters and metal temperature. The calculations are based on balance models and thermodynamic equations. The calculation scheme is shown in Fig. 1.

Specification of the initial data includes entering the following information: the input flow parameters; the process parameters; and the element distribution coefficients among phases.

The adopted process parameters are: t_m, t_sl, t_g – phase temperatures, °С, Q_loss ‒ heat losses to the environment, Q_drop – metal losses with metal droplets; η_CO – the degree of carbon oxidation to CO; η_FeO – the degree of iron oxidation to FeO; α – the oxygen utilization degree.

The element distribution coefficients among phases are specified on the basis of experimental data within the prescribed ranges of variation of the input and output flow parameters.

The following technical and economic indicators are used: E – process energy intensity, kW·h/t; С – production cost, RUB/t; PU – unit productivity, t/h; g_k – specific material consumption, kg/t.

Once all required parameters have been specified, an initialdata table for the input flows is generated. The input information includes the temperature, density, and flow rate of the k-th input flow. The procedure also requires the chemical composition of the charge materials to be specified. For all calculation variants, the software provides a baseline composition for the condensed and gaseous input flows, as well as for the volatile components of the charge; if necessary, this composition can be modified by the user.

Results and discussion

The static modes of the electric steelmaking process are calculated from the material and thermal balances, formulated on the basis of the laws of conservation of mass and energy for the components of a heterogeneous system. The calculation procedure for the material and thermal balances is outlined in Fig. 2.

At the level of input–output flows, the overall material balance for the system can be written as:

\[\sum\limits_{k = 1}^K {{G_k}}  = \sum\limits_{l = 1}^L {{G_l}} .\]

When phase separation is taken into account, the material-balance relationship can be expressed in the following form:

\[\sum\limits_{k = 1}^{{K^f}} {G_k^f}  + \sum\limits_{k = 1}^{{K^{\rm{g}}}} {G_k^{\rm{g}}}  = {G_{\rm{m}}} + {G_{{\rm{sl}}}} + {G_{\rm{g}}}.\]

The total mass of substances entering the furnace with the input flows is:

\[\sum\limits_{k = 1}^K {{G_k}}  = \sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^f} {\frac{{G_k^f{{\left| {{R_m}} \right|}_k}}}{{100}} + } } \sum\limits_{k = 1}^{{K^{\rm{g}}}} {\sum\limits_{m = 1}^{N_k^{\rm{g}}} {\frac{{G_k^{\rm{g}}{{\{ {R_m}\} }_k}}}{{100}}} } .\]

The mass of substances leaving the system with the output flows is defined as the sum of the masses contained in the metallic, slag, and gas phases:

\[\sum\limits_{l = 1}^L {{G_l}}  = \sum\limits_{n = 1}^{{N_{\rm{m}}}} {\frac{{{G_{\rm{m}}}\left[ {{R_n}} \right]}}{{100}} + } \sum\limits_{n = 1}^{{N_{{\rm{sl}}}}} {\frac{{{G_{{\rm{sl}}}}\left( {{R_n}} \right)}}{{100}} + } \sum\limits_{n = 1}^{{N_{\rm{g}}}} {\frac{{{G_{\rm{g}}}\left\{ {{R_n}} \right\}}}{{100}}} .\]

Accordingly, the material-balance equation at the level of substance flows takes the form:

\[\begin{array}{c}\sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^f} {\frac{{G_k^f{{\left| {{R_m}} \right|}_k}}}{{100}} + } } \sum\limits_{k = 1}^{{K^{\rm{g}}}} {\sum\limits_{m = 1}^{N_k^{\rm{g}}} {\frac{{G_k^{\rm{g}}{{\{ {R_m}\} }_k}}}{{100}}} }  = \\ = \sum\limits_{n = 1}^{{N_{\rm{m}}}} {\frac{{{G_{\rm{m}}}\left[ {{R_n}} \right]}}{{100}} + } \sum\limits_{n = 1}^{{N_{{\rm{sl}}}}} {\frac{{{G_{{\rm{sl}}}}\left( {{R_n}} \right)}}{{100}} + } \sum\limits_{n = 1}^{{N_{\rm{g}}}} {\frac{{{G_{\rm{g}}}\left\{ {{R_n}} \right\}}}{{100}}} .\end{array}\]

To determine the phase composition of the output flows, element balance equations are written for each element Е_i, since a given element may be present in different phases as a range of compounds:

\[\begin{array}{c}\sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^{E_i^f}} {\frac{{G_k^f{{\left| {{E_{i{x_m}}}{E_{j{y_m}}}} \right|}_k}}}{{100}}} \frac{{{x_m}{M_{{E_i}}}}}{{{M_{{E_{i{x_m}}}{E_{j{y_m}}}}}}}}  + \\ + \sum\limits_{k = 1}^{{K^{\rm{g}}}} {\sum\limits_{m = 1}^{N_k^{E_i^{\rm{g}}}} {\frac{{G_k^{\rm{}}{{\left\{ {{E_{i{x_m}}}{E_{j{y_m}}}} \right\}}_k}}}{{100}}} \frac{{{x_m}{M_{{E_i}}}}}{{{M_{{E_{i{x_m}}}{E_{j{y_m}}}}}}}}  = \\ = \frac{{{G_{\rm{m}}}[{E_i}]}}{{100}} + \sum\limits_{n = 1}^{N_{{\rm{sl}}}^{{_i}}} {\frac{{{G_{{\rm{sl}}}}\left( {{E_{i{x_n}}}{E_{j{y_n}}}} \right)}}{{100}}} \frac{{{x_n}{M_{{E_i}}}}}{{{M_{{E_{i{x_n}}}{E_{j{y_n}}}}}}} + \\ + \sum\limits_{n = 1}^{N_{\rm{g}}^{{E_i}}} {\frac{{{G_{\rm{g}}}\left\{ {{E_{i{x_n}}}{E_{j{y_n}}}} \right\}}}{{100}}} \frac{{{x_n}{M_{{E_i}}}}}{{{M_{{E_{i{x_n}}}{E_{j{y_n}}}}}}},\end{array}\]

where \(\left| {{E_{i{x_m}}}{E_{j{y_m}}}_k} \right|\), \(\left\{ {{E_{i{x_m}}}{E_{j{y_m}}}} \right\}\) ‒ the concentrations of the m-th substance containing element Е_i in k-th condensed and gaseous input flows, respectively, %; [E_i] ‒ the concentration of the substance consisting of element Е_i, in the metal, %; \(\left( {{E_{i{x_n}}}{E_{j{y_n}}}} \right)\), \(\left\{ {{E_{i{x_n}}}{E_{j{y_n}}}} \right\}\) – the concentrations of the n-th substance containing element Е_i in the slag and gas phases of the output flow, respectively, %; \(N_k^{E_i^f}\),  \(N_{{\rm{sl}}}^{{E_i}}\), \(N_{\rm{g}}^{{E_i}}\) – the numbers of substances containing element Е_i in the k-th input flow, slag, and gas; х_m, y_m – the stoichiometric coefficients of the m-th compound of element Е_i;  \({M_{{E_i}}}\), \({M_{{E_{i{x_m}}}{E_{j{y_m}}}}}\) – the molar masses of element Е_i and its compounds, kg/mol.

The total mass of the condensed substance R entering the system with the input flows is given by:

\[G_{\left| R \right|}^{{\rm{in}}} = \sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^f} {\frac{{G_k^f\left| {{R_m}_k} \right|}}{{100}}} } .\]

The mass of the gaseous substance R entering the system with the input flows is also determined taking into account its content in the gaseous input flows:

\[G_{\{ R\} }^{{\rm{in}}} = \sum\limits_{k = 1}^{{K^{\rm{g}}}} {\sum\limits_{m = 1}^{N_k^{\rm{g}}} {\frac{{G_k^{\rm{g}}{{\{ {R_m}\} }_k}}}{{100}}} } .\]

The phase composition of the output flow is determined as follows. In accordance with the element distribution coefficients among phases, the amount of element Е_i in the metal is determined by the following expression:

\[{G_{\left[ {{E_i}} \right]}} = G_{^{{_{ii}}}}^{{\rm{in}}}{L_{[{E_i}]}},\]

here \({L_{[{E_i}]}}\) – the distribution coefficient of element E_i in the metal.

The amount of the oxide of element Е_i in the slag is determined accordingly as

\[{G_{\left( {{E_{i{x_n}}}{{\rm{O}}_{j{y_n}}}} \right)}} = G_{{E_i}}^{{\rm{in}}}{L_{\left( {{E_i}} \right)}}\frac{{{M_{{E_{i{x_n}}}{{\rm{O}}_{j{y_n}}}}}}}{{{x_n}{M_{{E_i}}}}}.\]

Next, the amount of oxygen remaining in the system after oxidation of all components and consumed for iron oxidation is determined as follows:

\[\begin{array}{c}{G_{\rm{O}}} = \sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^{E_i^f}} {\frac{{G_k^f{{\left| {{E_{i{x_m}}}{{\rm{O}}_{{y_m}}}} \right|}_k}}}{{100}}} \frac{{0.016{y_m}}}{{{M_{{E_{i{x_m}}}{{\rm{O}}_{j{y_m}}}}}}}}  - \\ - \sum\limits_{n = 1}^{N_{{\rm{sl}}}^{{_i}}} {\frac{{{G_{({E_{i{x_n}}}{{\rm{O}}_{j{y_n}}})}}}}{{100}}} \frac{{0.016{y_n}}}{{{M_{{E_{i{x_n}}}{{\rm{O}}_{j{y_n}}}}}}}.\end{array}\]

The amount of iron oxides in the slag is then determined as:

\[\begin{array}{c}{G_{({\rm{FeO}})}} = G{}_{\rm{O}}{\eta _{{\rm{FeO}}}};\\{G_{({\rm{F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}})}} = G{}_{\rm{O}}(1 - {\eta _{{\rm{FeO}}}}).\end{array}\]

Accordingly, the amount of iron in the metal is calculated as follows:

\[{G_{[{\rm{Fe}}]}} = G_{{\rm{Fe}}}^{{\rm{in}}} - {G_{({\rm{FeO}})}}\frac{{0.056}}{{0.072}} - G_{{\rm{F}}{{\rm{e}}_{\rm{2}}}{{\rm{O}}_{\rm{3}}}}^{{\rm{in}}}\frac{{0.112}}{{0.160}}.\]

Consequently, the masses of metal and slag are determined as:

\[\begin{array}{c}{G_{Me}} = \sum\limits_{i = 1}^{{N_{Me}}} {{G_{[{E_i}]}}} ;\\{G_{{\rm{sl}}}} = \sum\limits_{i = 1}^{{N_{{\rm{sl}}}}} {{G_{({E_i}_{_{xn}}{E_{{i_{yn}}}})}}} .\end{array}\]

The calculation of the phase composition and masses in the ladle is performed in a similar manner; however, in this case the input flows consist of the metal produced in the furnace and slag that partially enters the ladle during tapping.

To calculate the composition of the gas-phase components, the following mechanism of off-gas formation in the electric furnace is proposed. For technologies involving the use of natural gas, complete combustion is assumed, which results in the chemical composition of the gases in the output flow corresponding to that obtained under classical decomposition conditions.

During complete combustion of natural gas, СО₂ and Н₂О are formed:

\[\begin{array}{l}G_{\{ {\rm{C}}{{\rm{O}}_2}\} }^{{\rm{}}} = G_{\{ {\rm{C}}{{\rm{H}}_4}\} }^{{\rm{}}}\left( {1 - {\eta _{{\rm{}}}}} \right)\frac{{0.044}}{{0.016}};\\G_{\{ {{\rm{H}}_2}{\rm{O}}\} }^{{\rm{}}} = G_{\{ {\rm{C}}{{\rm{H}}_4}\} }^{{\rm{}}}\left( {1 - {\eta _{{\rm{}}}}} \right)\frac{{0.018}}{{0.016}}.\end{array}\]

The amount of CO formed during combustion of the carbon contained in the charge can be determined as follows:

\[\begin{array}{l}G_{\{ {\rm{C}}{{\rm{O}}_2}\} }^{{\rm{comb}}} = G_{\{ {\rm{C}}{{\rm{H}}_4}\} }^{{\rm{in}}}\left( {1 - {\eta _{{\rm{conv}}}}} \right)\frac{{0.044}}{{0.016}};\\G_{\{ {{\rm{H}}_2}{\rm{O}}\} }^{{\rm{comb}}} = G_{\{ {\rm{C}}{{\rm{H}}_4}\} }^{{\rm{in}}}\left( {1 - {\eta _{{\rm{conv}}}}} \right)\frac{{0.018}}{{0.016}}.\end{array}\]

Taking into account the combustion of natural gas, the amount of СО₂ in the off-gases is given by:

\[{G_{\{ {\rm{C}}{{\rm{O}}_{\rm{2}}}\} }} = (1 - {{\rm{\eta }}_{{\rm{CO}}}})\left( {\sum\limits_{k = 1}^{{K^f}} {\frac{{G_k^f{{\left|  \right|}_k}}}{{100}} - \frac{{{G_{\rm{m}}}\left[ C \right]}}{{100}}} } \right)\frac{{0.044}}{{0.012}} + G_{{\rm{\{ C}}{{\rm{O}}_{\rm{2}}}{\rm{\} }}}^{{\rm{comb}}}.\]

The total amount of hydrogen in the off-gases is:

\[{G_{\{ {{\rm{H}}_{\rm{2}}}\} }} = G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{\} }}}^{{\rm{in}}}.\]

The amount of water vapor is determined as

\[{G_{\{ {{\rm{H}}_{\rm{2}}}{\rm{O}}\} }} = G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{O\} }}}^{{\rm{in}}} + G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{O\} }}}^{{\rm{comb}}}.\]

The amount of nitrogen in the off-gases is equal to the amount of nitrogen entering the system with the input flows per unit time:

\[{G_{\{ {{\rm{N}}_{\rm{2}}}\} }} = G_{{\rm{\{ }}{{\rm{N}}_{\rm{2}}}{\rm{\} }}}^{{\rm{in}}}.\]

The amount of SO₂ in the off-gases is determined in accordance with the sulfur transfer coefficient to the gas phase:

\[{G_{\{ {\rm{S}}{{\rm{O}}_{\rm{2}}}\} }} = G_{\rm{S}}^{{\rm{in}}}{{\rm{\alpha }}_{{\rm{\{ S\} }}}}\frac{{0.064}}{{0.032}}.\]

The total mass of gas is determined as follows:

\[{G_{\rm{g}}} = G_{{\rm{\{ CO\} }}}^{{\rm{out}}} + G_{{\rm{\{ C}}{{\rm{O}}_{\rm{2}}}{\rm{\} }}}^{{\rm{out}}} + G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{\} }}}^{{\rm{out}}} + G_{{\rm{\{ }}{{\rm{H}}_{\rm{2}}}{\rm{\} }}}^{{\rm{out}}} + G_{{\rm{\{ S}}{{\rm{O}}_{\rm{2}}}{\rm{\} }}}^{{\rm{out}}} + G_{{\rm{\{ }}{{\rm{N}}_{\rm{2}}}{\rm{\} }}}^{{\rm{out}}}.\]

When deriving the thermal balance equations, it is assumed that the principal processes governing the thermal state of the system are: the sensible heat of the charge materials; heat exchange with the surrounding environ-ment; heat released by electric arc combustion; and chemical reactions with their associated thermal effects. The thermal balance equations are formulated on the basis of the law of conservation of energy, expressed as Q_in = Q_out.

Taking into account the enthalpy of the input and output flows, the total heat of chemical reactions occurring in the system, the heat supplied by the electric arc, as well as heat exchange with the environment, the thermal-balance equation can be written in the following form:

\[\sum\limits_{k = 1}^{{K^f}} {G_k^f\Delta H_k^f}  + \sum\limits_{k = 1}^{{K^{\rm{g}}}} {G_k^{\rm{}}} \Delta H_k^{\rm{g}} + {Q_{{\rm{arc}}}} = \sum\limits_{l = 1}^L {{G_l}\Delta {H_l}}  + \Delta {H_{{\rm{c}}{\rm{}}{\rm{r}}}} + {Q_{{\rm{loss}}}},\]

where \(\Delta H_k^f\), \(\Delta H_k^{\rm{g}}\), ΔH_l ‒ the enthalpies per unit mass of the k-th condensed or gaseous input flow and the l-th output flow, respectively, referred to standard conditions and a temperature of 298 K; Q_arc ‒ the heat input to the system from electric arc combustion; Q_loss ‒ heat losses to the environment; ΔН_cr ‒ the total thermal effect of the chemical reactions.

Only liquid pig iron has a nonzero enthalpy; therefore, the enthalpy per unit mass of liquid pig iron relative to T = 298 K is given by:

\[\Delta {H_{{\rm{pgi}}}} = \sum\limits_{m = 1}^{{N_{{\rm{pgi}}}}} {{{\left( {\Delta H_T^0} \right)}_m}\frac{{{{[R]}_m}_{_{{\rm{pgi}}}}}}{{100{M_{{R_m}}}}}} ,\]

where \({\left( {\Delta H_T^0} \right)_m}\) ‒ the enthalpy change of the m-th substance of liquid pig iron upon heating from 298 K to T_k, kJ/mol; \({[R]_m}_{_{{\rm{pgi}}}}\) ‒ the concentration of substance R_m, %; \({M_{{R_m}}}\) ‒ is the molar mass of substance R_m, kg/mol.

The enthalpies per unit mass of metal, slag, and gas are determined, respectively, as follows:

\[\begin{array}{c}\Delta {H_{\rm{m}}} = \sum\limits_{n = 1}^{{N_{\rm{m}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{[{R_n}]}}{{100{M_{{R_n}}}}}} ;\\\Delta {H_{{\rm{sl}}}} = \sum\limits_{n{\rm{ }} = {\rm{ }}1}^{{N_{{\rm{sl}}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{({R_n})}}{{100{M_{{R_n}}}}}} ;\\\Delta {H_{\rm{g}}} = \sum\limits_{n{\rm{ }} = {\rm{ }}1}^{{N_{\rm{g}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{\{ {R_n}\} }}{{100{M_{{R_n}}}}}} .\end{array}\]

The thermal effect of chemical reactions is defined as the sum of the thermal effects of independent reactions describing the transition of the system from the initial to the final state:

\[\Delta {H_{{\rm{c}}{\rm{}}{\rm{r}}}} = \sum\limits_{w = 1}^W {\Delta {H_w}} ,\]

where W – the number of independent reactions; \(\Delta {H_w} = \Delta H_w^0\Delta {n_{{R_w}}}\) – the thermal effect of the w-th chemical reaction, kJ/mol; \(\Delta H_w^0\) ‒ the standard thermal effect of the w-th chemical reaction; \(\Delta {n_{{R_w}}}\) ‒ the number of moles of substance R that reacted in the w-th reaction.

The number of moles of the reacting substance R_w is determined as the difference between its amounts in the input and output flows:

\[\Delta {n_{{R_w}}} = \sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} .\]

The heat released by arc combustion is determined taking into account the electric energy consumption:

Q_arc = 3600E,

where Е – the electric energy consumption, kW·h.

Taking the above into account, the thermal-balance equation can be written in the following form:

\[\begin{array}{c}\sum\limits_{m = 1}^{{N_{\rm{pgi}}}_{{\rm{pgi}}}} {{{\left( {\Delta H_T^0} \right)}_m}\frac{{{{[R]}_m}_{_{{\rm{}}}}}}{{100{M_{{R_m}}}}}}  + \\ + \sum\limits_{w = 1}^{W{\rm{exo}}} {\Delta H_w^0} \left( {\sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} } \right) + {Q_{{\rm{arc}}}} = \\ = \sum\limits_{n = 1}^{{N_{\rm{m}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{{G_{\rm{m}}}\left[ {{R_n}} \right]}}{{100{M_{{R_n}}}}} + } \sum\limits_{n = 1}^{{N_{{\rm{sl}}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{{G_{{\rm{sl}}}}\left( {{R_n}} \right)}}{{100{M_{{R_n}}}}} + } \\ + \sum\limits_{w = 1}^{W{\rm{endo}}} {\Delta H_w^0\left( {\sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} } \right)}  + {Q_{{\rm{пот}}}}.\end{array}\]

The principal heat inputs in the thermal balance include the heat of liquid pig iron, the heat of exothermic oxidation reactions of charge components with gaseous oxygen, the heat of slag-forming reactions, and the heat released by arc combustion. The heat expenditures include heat required for heating the metal, slag, and gas; heat consumed for decomposition of carbonates and iron oxides; heat required for moisture evaporation; and heat losses to the environment.

The enthalpies of the input and output flows were calculated using the following reference data: coefficients of the approximation equation for the heat capacity of a substance (c₀, c_–1, c₁, c₂, c₃), values of the enthalpy of formation and entropy at standard temperature (\({\Delta _f}H_{298}^0\), \(S_{298}^0\)), and data on phase transitions (Т_ft, \(\Delta H_{{\rm{f}}{\rm{t}}}^0\)) for individual substances.

The solution of the optimization problem using formal methods involves selecting appropriate criteria and defining a system of constraints, including requirements for metal composition, allowable ranges of variation in the consumption rates of charge-material components and system state parameters, compliance with the law of conservation of mass at the levels of flows, substances, and elements, and compliance with the law of conservation of energy.

The following indicators may be used as optimization criteria:

– total consumption (TC) of charge materials per unit of product, kg/t,

\[{\rm{TC}} = \sum\limits_{k = 1}^K {{g_k} = } {\rm{ }}\frac{{\sum\limits_{k = 1}^K {{G_k}} }}{{{G_{\rm{m}}}}} \cdot 1000 \to {\rm{min}};\]

– production cost (C), RUB/t,

\[{\rm{C}} = \frac{{\sum\limits_{k = 1}^K {{G_k}{{\rm{P}}_k}} }}{{{G_{\rm{m}}}}} + {\rm{O}}{\rm{H}} + {\rm{P}}{\rm{C}} \to {\rm{min}};\]

– energy consumption (E) per unit of product, GJ/t,

\[{\rm{E}} = \frac{{\sum\limits_{k = 1}^K {{G_k}{{\rm{E}}_k}} }}{{{G_{\rm{m}}}}} \to {\rm{min}};\]

– unit productivity (PU)

\[{\rm{PU}} = {G_{\rm{m}}} = \sum\limits_{n = 1}^{{N_{\rm{m}}}} {G_{[{R_n}]}^{{\rm{out}}}}  \to {\rm{max}}{\rm{,}}\]

where P_k – the price of the k-th input material, RUB/t; OH – general plant overhead costs, RUB/t; PC ‒ processing costs, RUB/t; E_k – is the specific energy intensity of the k-th material, GJ/t.

The formulation of the optimization problem consists in finding an extremum of one of the selected criteria subject to the following constraints:

– on the ranges of variation in charge-material consumption rates:

G_{k min} < G_k < G_{k max};

– on metal and slag parameters:

[R_n]_min < [R_n] < [R_n]_max (n = 1 ÷ N_m);

(R_n)_min < (R_n) < (R_n)_max (n = 1 ÷ N_sl);

T_{l min} < T_l < T_{l max} (l = 1 ÷ L);

‒ compliance with the law of conservation of mass at the levels of flows, substances, and elements:

\[\begin{array}{c}\sum\limits_{k = 1}^{{K^f}} {G_k^f}  + \sum\limits_{k = 1}^{{K^{\rm{g}}}} {G_k^{\rm{g}}}  = {G_{\rm{m}}} + {G_{{\rm{sl}}}} + {G_{\rm{g}}};\\\sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^f} {\frac{{G_k^f{{\left| {{R_m}} \right|}_k}}}{{100}} + } } \sum\limits_{k = 1}^{{K^{\rm{g}}}} {\sum\limits_{m = 1}^{N_k^{\rm{g}}} {\frac{{G_k^{\rm{g}}{{\{ {R_m}\} }_k}}}{{100}}} }  = \\ = \sum\limits_{n = 1}^{{N_{\rm{m}}}} {\frac{{{G_{\rm{m}}}\left[ {{R_n}} \right]}}{{100}} + } \sum\limits_{n = 1}^{{N_{{\rm{sl}}}}} {\frac{{{G_{{\rm{sl}}}}\left( {{R_n}} \right)}}{{100}} + } \sum\limits_{n = 1}^{{N_{\rm{g}}}} {\frac{{{G_{\rm{g}}}\left\{ {{R_n}} \right\}}}{{100}}} ;\\\sum\limits_{k = 1}^{{K^f}} {\sum\limits_{m = 1}^{N_k^{E_i^f}} {\frac{{G_k^f{{\left| {{E_{i{x_m}}}{E_{j{y_m}}}} \right|}_k}}}{{100}}} \frac{{{x_m}{M_{{E_i}}}}}{{{M_{{E_{i{x_m}}}{E_{j{y_m}}}}}}}}  + \\ + \sum\limits_{k = 1}^{{K^{\rm{g}}}} {\sum\limits_{m = 1}^{N_k^{E_i^{\rm{g}}}} {\frac{{G_k^{\rm{g}}{{\left\{ {{E_{i{x_m}}}{E_{j{y_m}}}} \right\}}_k}}}{{100}}} \frac{{{x_m}{M_{{E_i}}}}}{{{M_{{E_{i{x_m}}}{E_{j{y_m}}}}}}}}  = \\ = \frac{{{G_{\rm{m}}}[{E_i}]}}{{100}} + \sum\limits_{n = 1}^{N_{{\rm{sl}}}^{{_i}}} {\frac{{{G_{{\rm{sl}}}}\left( {{E_{i{x_n}}}{E_{j{y_n}}}} \right)}}{{100}}} \frac{{{x_n}{M_{{E_i}}}}}{{{M_{{E_{i{x_n}}}{E_{j{y_n}}}}}}} + \\ + \sum\limits_{n = 1}^{N_{\rm{g}}^{{E_i}}} {\frac{{{G_{\rm{g}}}\left\{ {{E_{i{x_n}}}{E_{j{y_n}}}} \right\}}}{{100}}} \frac{{{x_n}{M_{{E_i}}}}}{{{M_{{E_{i{x_n}}}{E_{j{y_n}}}}}}};\end{array}\]

‒ compliance with the law of conservation of energy:

\[\begin{array}{c}\sum\limits_{m = 1}^{{N_{{\rm{pgi}}}}} {{{\left( {\Delta H_T^0} \right)}_m}\frac{{{{[R]}_m}_{_{{\rm{pgi}}}}}}{{100{M_{{R_m}}}}}}  + \\ + \sum\limits_{w = 1}^{W{\rm{exo}}} {\Delta H_w^0} \left( {\sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} } \right) + {Q_{{\rm{arc}}}} = \\ = \sum\limits_{n = 1}^{{N_{\rm{m}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{{G_{\rm{m}}}\left[ {{R_n}} \right]}}{{100{M_{{R_n}}}}} + } \sum\limits_{n = 1}^{{N_{{\rm{sl}}}}} {{{\left( {\Delta H_T^0} \right)}_n}\frac{{{G_{{\rm{sl}}}}\left( {{R_n}} \right)}}{{100{M_{{R_n}}}}} + } \\ + \sum\limits_{w = 1}^{W{\rm{endo}}} {\Delta H_w^0} \left( {\sum\limits_{k = 1}^K {\frac{{{G_k}{R_{kw}}}}{{100{M_{{R_w}}}}} - } \sum\limits_{l = 1}^L {\frac{{{G_l}{R_{lw}}}}{{100{M_{{R_w}}}}}} } \right) + {Q_{{\rm{loss}}}};\end{array}\]

‒ fulfillment of at least one of the following target conditions:

CP_min < CP < CP_max;

C_min < C < C_max;

E_min < E < E_max;

PU_min < PU < PU_max.

Thus, a method for mathematical modeling and optimization of the electric melting process has been developed, providing a systematic solution to a set of interrelated optimization problems.

Conclusions

The electric steelmaking process was analyzed, and a method for its mathematical modeling and optimization was developed. The proposed approach is distinguished by a systematic treatment of a set of interrelated optimization problems, enabling the determination of acceptable process conditions within the metallurgical system using modeling and optimization methods. In addition, technological operating modes for implementing the electric melting technology are proposed.