Перейти к:
Критерии существования локальных равновесий в переохлажденных расплавах
https://doi.org/10.17073/0368-0797-2025-6-607-612
Аннотация
Статья предназначена для исследователей, работающих в области переохлажденных расплавов. В ней рассматривается важный теоретический вопрос, связанный с возможностью установления локального термодинамического равновесия на границе раздела фаз при кристаллизации из переохлажденных металлических расплавов. Такие процессы играют ключевую роль в формировании структуры материалов при их затвердевании, особенно в условиях быстрого охлаждения, характерных для современных технологий металлургии и порошковой металлургии. При переохлаждении в расплаве начинают формироваться зародыши новой твердой фазы. Для математического описания роста зародыша необходимо задать граничные условия, определяющие состав прилегающей жидкой фазы. В традиционных подходах предполагается, что вблизи зародыша может быть установлено локальное равновесие, параметры которого извлекаются из равновесной диаграммы состояния. Однако, как показали исследования авторов для двухкомпонентных систем, в некоторых случаях локальное равновесие невозможно в принципе. В данной работе проведен теоретический анализ условий равновесия. Для этого рассматривались химические потенциалы компонентов обеих фаз: твердого зародыша и жидкого расплава. По равновесной диаграмме состояния соответствующей макросистемы можно составить представление о химических потенциалах их компонентов, в частности, в какой фазе химический потенциал каждого компонента ниже. Показано, что, когда зародыш новой фазы состоит из одного компонента, такое локальное равновесие, в принципе, всегда возможно. Однако, когда зародыш является раствором, такое возможно лишь при определенных условиях. В этих случаях применение граничных условий первого рода становится некорректным, и необходимо учитывать скорости химических реакций перехода каждого компонента из одной фазы в другую.
Ключевые слова
Для цитирования:
Дрозин А.Д., Дудоров М.В. Критерии существования локальных равновесий в переохлажденных расплавах. Известия высших учебных заведений. Черная Металлургия. 2025;68(6):607-612. https://doi.org/10.17073/0368-0797-2025-6-607-612
For citation:
Drozin A.D., Dudorov M.V. Criteria for the existence of local equilibria in supercooled melts. Izvestiya. Ferrous Metallurgy. 2025;68(6):607-612. https://doi.org/10.17073/0368-0797-2025-6-607-612
Введение
Изучение кинетики образования и роста кристаллов при сверхбыстром охлаждении расплава стало особенно актуальным в последнее время в связи с развитием нанотехнологий и широким применением аморфных сплавов. Для расчета скоростей роста нанокристаллов [1 – 3] в расплаве или, например, в аморфном сплаве при отжиге [4 – 5] нужно знать концентрации компонентов расплава на их поверхностях.
Целью настоящей работы является теоретический анализ условий, при которых локальное равновесие может (или не может) быть установлено на границе между твердым зародышем и переохлажденным расплавом.
Рассмотрим случай, когда двухкомпонентный металлический расплав моментально охлаждается до температуры ниже температуры солидус. В нем начинают образовываться зародыши новой фазы – твердого металла. Для составления дифференциальных уравнений, определяющих процесс роста этого зародыша, необходимо задать граничные условия, в данном случае, концентрации компонентов жидкого расплава на границе раздела фаз. Традиционно предполагается, что всякая система стремится прийти в равновесное состояние и, хотя настоящего равновесия в переохлажденном жидком расплаве быть не может, можно считать, что на нано расстояниях от зародыша состав жидкой фазы будет почти равновесным – установится локальное равновесие. Данные об этом равновесии можно получить из равновесной диаграммы состояния. Однако, как показало исследование авторов данной статьи, во многих случаях такое приближение некорректно.
Полученные нами выводы об отклонении от локального равновесия подтверждаются результатами исследований эффектов «захвата примеси», обусловленных высокой скоростью роста кристаллов в расплаве [6 – 9]. Теоретические исследования ряда авторов [10 – 13], а также наши исследования [14 – 15] позволяют выявить некоторые закономерности протекания указанных процессов. Экспериментальные исследования различных систем [16 – 17], в частности переохлажденных металлических расплавов [18 – 20], подтверждают проявление таких эффектов на практике. Между тем до настоящего времени не были сформулированы общие термодинамические критерии, позволяющие оценить условия локального равновесия при росте кристаллов. Настоящая работа посвящена такому исследованию.
Для оценки условий равновесия рассмотрим процессы, связанные с равновесием фаз через химические потенциалы их компонентов:
| \[{\mu _i} = \mu _i^0 + RT\ln {a_i},\] | (1) |
где \(\mu _i^0\) – не зависящая от концентраций часть химического потенциала i-го компонента, R – универсальная газовая постоянная, T – температура, ai – активность i-го компонента. Для общности рассмотрения из всех свойств химических потенциалов используем только следующие:
– зависимость активности компонента фазы от концентрации этого компонента является монотонно возрастающей непрерывной функцией;
– при концентрации компонента, стремящейся к нулю, его активность также стремится к нулю, следовательно, из уравнения (1), значение химического потенциала стремится к минус бесконечности. При этом вклад этого компонента в свободную энергию Гиббса фазы также стремится к нулю.
Двухкомпонентная система с равновесием по одному компоненту
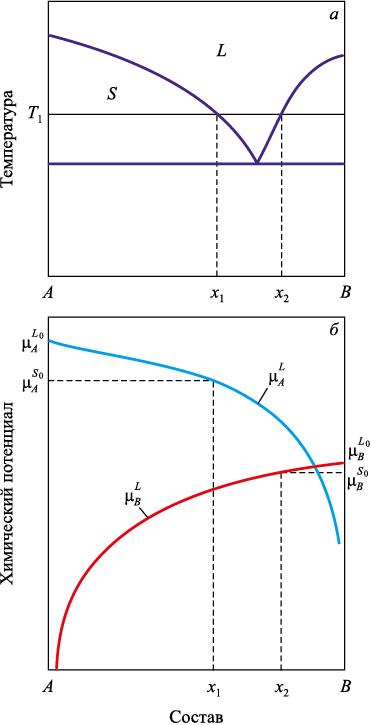
Рассмотрим модельный случай жидкого раствора (расплава) компонентов A и B с равновесной диаграммой состояния, изображенной на рис. 1, при температуре T1 . На основании диаграммы можно сделать ряд заключений о химических потенциалах компонентов фаз. Поскольку при доле компонента B, соответствующей чистому компоненту A, система в равновесии находится в твердом состоянии, химический потенциал компонента A в твердой фазе должен быть ниже, чем в жидкой фазе: \(\mu _A^{{S_0}} < \mu _A^{{L_0}}\). Обозначим символом x долю компонента B соответствующей фазе и проведем, в соответствии с приведенными выше положениями, линию \(\mu _A^L = \mu _A^L(x)\).
Рис. 1. Диаграмма состояния (а) и химические потенциалы компонентов системы (б) |
Поскольку, в соответствии с уравнением (1), при x → 1 химический потенциал \(\mu _A^L\) → –∞ и \(\mu _A^L\)(0) больше \(\mu _A^S\)(0), то по теореме Больцано-Коши для непрерывных функций [21] существует точка x, где \(\mu _A^L\)(x) = \(\mu _A^{{S_0}}\). В показанном на рис. 1 случае для температуры T1 это концентрация x1 .
Заметим, что эти же рассуждения справедливы и для температур ниже эвтектической. Локальное равновесие будет устанавливаться между зародышем твердой фазы и жидкой фазой, имеющей состав, соответствующий продолжению линии ликвидуса. Это положение применимо при наличии аппроксимации (или аналитического выражения) линии ликвидуса ниже линии солидус.
Анализ ограничился компонентом A, поскольку компонент B в зародыше отсутствует и его химический потенциал не влияет на фазовое равновесие. Aналогичные рассуждения можно провести для роста кристалла фазы B.
В соответствии с рис. 1, при температуре T1 зародыши из чистого компонента B находятся в локальном равновесии с раствором состава x2.
Двухкомпонентная система с равновесием по двум компонентам
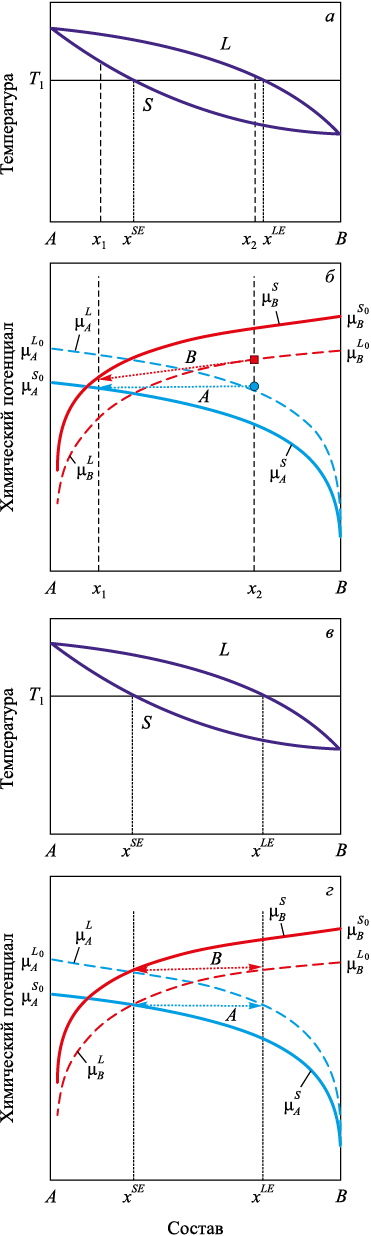
Рассмотрим следующий, более сложный случай. Пусть компоненты A и B обладают неограниченной взаимной растворимостью в жидком и твердом состояниях в соответствии с диаграммой на рис. 2.
Рис. 2. Диаграммы состояния (а, в) и химические потенциалы компонентов |
Исходя из диаграммы (рис. 2, а), сделаем нужные заключения о химических потенциалах компонентов при температуре T1 . Поскольку при доле компонента B, соответствующей чистому компоненту A: x = 0, система в равновесии находится в твердом состоянии, то химический потенциал компонента A в твердой фазе \(\mu _A^{{S_0}}\) должен быть меньше, чем химический потенциал компонента A в жидкой фазе \(\mu _A^{{L_0}}\), как это и отображено на рис. 2, б. Проведем в соответствии с уравнением (1) линии \(\mu _A^L\) = \(\mu _A^L\)(x) и \(\mu _A^S\) = \(\mu _A^S\)(x). В общем случае, линия \(\mu _A^L\) должна лежать выше и правее линии \(\mu _A^S\). Проведем аналогичные построения с величинами, относящимися к компоненту B. Так как при концентрации x = 1, соответствующей чистому компоненту B, система в равновесии находится в жидком состоянии, то химический потенциал компонента B в жидкой фазе \(\mu _B^{{L_0}}\) должен быть меньше, чем химический потенциал компонента B в твердой фазе \(\mu _B^{{S_0}}\), как это и отображено на рис. 2, б. Проведем в соответствии с уравнением (1) линии \(\mu _B^L\) = \(\mu _B^L\)(x) и \(\mu _B^S\) = \(\mu _B^S\)(x). В общем случае линия \(\mu _B^S\) должна лежать выше и левее линии \(\mu _B^L\).
Заметим также, что взаимное расположение химических потенциалов компонентов A и B не имеет значения для наших рассуждений.
Чтобы система находилась в равновесии по компоненту A, необходимо, чтобы составы жидкой и твердой фаз были такими, что \(\mu _A^L\left( {c_A^L} \right) = \mu _A^S\left( {c_A^S} \right)\). Геометрически это означает, что составы, определяемые точками пересечения линий \(\mu _A^L\)(x) и \(\mu _A^S\)(x) с любой горизонтальной прямой будут равновесными по компоненту A. Таких пар составов бесконечное множество.
Однако для равновесия системы необходимо еще и равновесие по компоненту B при тех же концентрациях. Так, если состав твердой фазы будет соответствовать точке x1 на рис. 2, б, то, несмотря на то, что химические потенциалы компонента A в обеих фазах будут равны, по компоненту B равновесие не достигнется. Химический потенциал компонента B в жидкой фазе больше, чем в твердой, и будет происходить переход компонента B из жидкой фазы в твердую. Равновесие по компоненту A нарушится и состав твердой фазы изменится. В случае, представленном на рис. 2, б, в результате перераспределения концентраций обе фазы будут обогащаться компонентом B. Этот процесс закончится лишь тогда, когда точка x1 займет положение xSE, а x2 – положение xLE.
Выясним, когда возможно подлинное равновесие – по обоим компонентам. При равновесии должны одновременно выполняться равенства: \(\mu _A^L\left( {{x^L}} \right) = \mu _A^S\left( {{x^S}} \right)\) и \(\mu _B^L\left( {{x^L}} \right) = \mu _B^S\left( {{x^S}} \right)\), где xL и xS доли компонента B в жидкой и твердой фазах соответственно. Как видно из рис. 2, в, г, для этого необходимо и достаточно, чтобы химические сродства реакций перехода из жидкой фазы в твердую компонента A: \({a_A} = \mu _A^{{L_0}} - \mu _A^{{S_0}}\) и компонента B: \({a_B} = \mu _B^{{L_0}} - \mu _B^{{S_0}}\) имели разные знаки, т. е. либо \(\left( {\mu _A^{{L_0}} < \mu _A^{{S_0}},\,\,\,\mu _B^{{L_0}} > \mu _B^{{S_0}}} \right)\), либо \(\left( {\mu _A^{{L_0}} > \mu _A^{{S_0}},\,\,\,\mu _B^{{L_0}} < \mu _B^{{S_0}}} \right)\).
Докажем это математически. Для простоты рассмотрим случай, когда активности компонентов равны их мольным долям. При равновесии должны одновременно выполняться равенства: \(\mu _A^L\left( {{x^L}} \right) = \mu _A^S\left( {{x^S}} \right)\) и \(\mu _B^L\left( {{x^L}} \right) = \mu _B^S\left( {{x^S}} \right)\). Используя уравнение (1), запишем эти соотношения в виде:
| \[\begin{array}{c}\left\{ \begin{array}{l}\mu _A^{{L_0}} + RT\ln \left( {1 - {x^L}} \right) = \mu _A^{{S_0}} + RT\ln \left( {1 - {x^S}} \right),\\\mu _B^{{L_0}} + RT\ln {x^L} = \mu _B^{{S_0}} + RT\ln {x^S}\end{array} \right. \Rightarrow \\ \Rightarrow \left\{ \begin{array}{l}\frac{{1 - {x^L}}}{{1 - {x^S}}} = \exp \left( {\frac{{\mu _A^{{S_0}} - \mu _A^{{L_0}}}}{{RT}}} \right),\\\frac{{{x^L}}}{{{x^S}}} = \exp \left( {\frac{{\mu _B^{{S_0}} - \mu _B^{{L_0}}}}{{RT}}} \right).\end{array} \right.\end{array}\] | (2) |
Введем обозначения
| \[\begin{array}{c}A_A^0 = \mu _A^{{L_0}} - \mu _A^{{S_0}},\,\,\,A_B^0 = \mu _B^{{L_0}} - \mu _B^{{S_0}},\\{K_A} = \exp \left( { - \,\,\frac{{A_A^0}}{{RT}}} \right),\,\,{K_B} = \exp \left( { - \,\,\frac{{A_B^0}}{{RT}}} \right).\end{array}\] | (3) |
Из системы уравнений (2) следует, что не может быть KA = 1 или KB = 1 или KA = KB , так как тогда получается, что KA = KB = 1 и xL = xS, что в данном случае не реализуется.
За исключением этих вариантов, из уравнения (2) получаем
| \[{x^S} = \frac{{{K_A} - 1}}{{{K_A} - {K_B}}},\,\,\,{x^L} = \frac{{{K_A} - 1}}{{{K_A} - {K_B}}}{K_B}.\] | (4) |
Однако из формул (4) могут получиться и физически нереальные результаты (отрицательные или большие единицы). Выясним, при каких значениях KA и KB будет выполняться 0 ≤ xS ≤ 1, 0 ≤ xL ≤ 1, т. е.
| \[0 \le \frac{{{K_A} - 1}}{{{K_A} - {K_B}}} \le 1,\,\,\,0 \le \frac{{{K_A} - 1}}{{{K_A} - {K_B}}}{K_B} \le 1.\] | (5) |
Исследование системы неравенств (5) показывает, что они выполняются в случаях, когда (KA < 1, KB > 1), либо, наоборот, (KA > 1, KB < 1). С учетом обозначений, приведенных в уравнении (3), получаем, что равновесие в расматриваемой системе возможно, если химические сродства \(A_A^0\) и \(A_B^0\) имеют разные знаки: если для одного компонента, например, для A: \(\mu _A^{{L_0}}\) > \(\mu _A^{{S_0}}\), то для второго должно быть обязательно наоборот: \(\mu _B^{{L_0}}\) < \(\mu _B^{{S_0}}\). Таким образом, критерием возможности локального равновесия являются условия
| \[\left( {\mu _A^{{L_0}} < \mu _A^{{S_0}},\,\,\mu _B^{{L_0}} > \mu _B^{{S_0}}} \right)\] или \[\left( {\mu _A^{{L_0}} > \mu _A^{{S_0}},\,\,\,\mu _B^{{L_0}} < \mu _B^{{S_0}}} \right).\] | (6) |
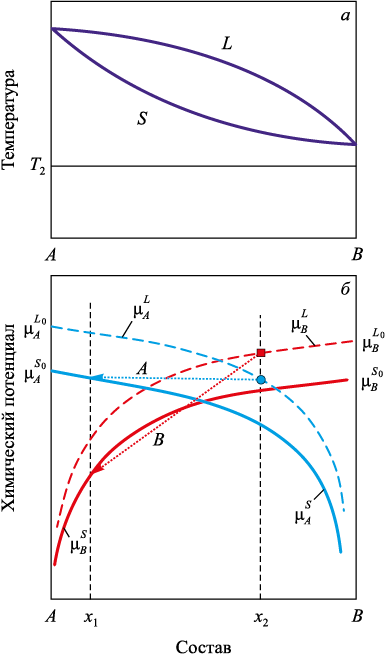
Рассмотрим случай, когда эти условия не выполняются: та же система при температуре T2 ниже линии солидус (рис. 3).
Рис. 3. Диаграмма состояния (а) и химические потенциалы компонентов (б) |
При температуре ниже линии солидус оба компонента в чистом виде находятся в твердом состоянии: \(\left( {\mu _A^{{L_0}} > \mu _A^{{S_0}},\,\,\mu _B^{{L_0}} > \mu _B^{{S_0}}} \right)\,\) и необходимые условия равновесия фаз не выполняются. Это видно из рис. 3, так как кривая \(\mu _A^{{L_0}}\) находится выше и правее кривой \(\mu _A^{{S_0}}\) при равновесии по компоненту A xS < xL.
Для компонента B кривая \(\mu _B^{{L_0}}\) находится выше и левее кривой \(\mu _B^{{S_0}}\) и равновесие по компоненту B возможно, только если xL < xS. Вместе эти условия выполняться не могут – равновесие невозможно.
Таким образом, при температурах ниже линии солидус, когда оба компонента находятся в твердом состоянии, условия равновесия по обоим компонентам не могут быть выполнены одновременно. Анализ показывает, что в этом случае любое локальное равновесие между жидкой и твердой фазами невозможно, поскольку оно требует противоречивых значений химических потенциалов. Следовательно, любые попытки аналитического продолжения равновесных линий в область твердых переохлажденных расплавов не имеют термодинамического обоснования и не могут быть использованы для корректного описания фазовых переходов при переохлаждении.
Обсуждение результатов исследования
Целью данной работы являлось использование равновесных диаграмм состояния для изучения динамики зародышеобразования и роста зародышей новой фазы. Очевидно, что при быстром охлаждении система не достигает глобального равновесия, однако в окрестности границы между твердой и жидкой фазами может устанавливаться квазиравновесное локальное состояние, что позволяет использовать термодинамические подходы. Использование локальных равновесий является важным принципом неравновесной термодинамики.
Проведенный анализ показал, что такие локальные равновесия возможны не всегда. В случае, если зародыш состоит из одного компонента, квазиравновесное описание применимо. При наличии двух и более компонентов возможность локального равновесия определяется соотношением показателей химического сродства перехода между фазами. В частности, если данные показатели имеют одинаковый знак, локальное равновесие невозможно, и фазовые переходы должны описываться исключительно с использованием кинетических моделей.
Предложенный подход может быть обобщен на более сложные системы при наличии функциональных зависимостей активностей компонентов фаз от состава. В дальнейшем для более точного моделирования роста зародышей требуется дополнение модели уравнениями диффузии, описывающими перенос вещества к границе раздела фаз и уравнениями, определяющими скорости химических реакций перехода компонентов между фазами.
Выводы
Разработан метод определения возможности существования локального равновесия между твердым зародышем и жидкой (маточной) фазой на основе анализа химических потенциалов компонентов. С необходимыми модификациями данный подход может быть применен к реальным многокомпонентным системам. В тех случаях, когда установление локального равновесия невозможно, математическое описание процесса кристаллизации должно включать не только уравнения диффузии, но и уравнения, описывающие скорости межфазных химических реакций для каждого компонента.
Список литературы
1. Tan L., Zabaras N. Modeling the growth and interaction of multiple dendrites in solidification using a level set method. Journal of Computational Physics. 2007;226(1):131–155. https://doi.org/10.1016/j.jcp.2007.03.023
2. Boettinger W.J., Warren J.A., Beckermann C., Karma A. Phase-field simulation of solidification. Annual Review of Material Research. 2002;32:163–194. https://doi.org/10.1146/annurev.matsci.32.101901.155803
3. Дрозин А.Д. Рост микрочастиц продуктов химических реакций в жидком растворе. Челябинск: Издательство ЮУрГУ; 2007:56.
4. Herlach D.M., Galenko P.K., Holland-Moritz D. Metastable Solids from Undercooled Melts. Amsterdam; London: Elsevier; 2007:432.
5. Gamov P.A., Drozin A.D., Dudorov M.V., Roshchin V.E. Model for nanocrystal growth in an amorphous alloy. Russian Metallurgy (Metally). 2012;2012(11):1002–1006. https://doi.org/10.1134/S0036029512110055
6. Baker J.C., Gahn J.W. Solute trapping by rapid solidification. Acta Metallurgica. 1969;17(5):575–578. https://doi.org/10.1016/0001-6160(69)90116-3
7. Aziz M.J. Model for solute redistribution during rapid solidification. Journal of Applied Physics. 1982;53(2):1158–1168. https://doi.org/10.1063/1.329867
8. Aziz M.J., Kaplan T. Continuous growth model for interface motion during alloy solidification. Acta Metallurgica. 1988;36(8):2335–2347. https://doi.org/10.1016/0001-6160(88)90333-1
9. Jackson K.A., Beatty K.M., Gudgel K.A. An analytical model for non-equilibrium segregation during crystallization. Journal of Crystal Growth. 2004;271(3–4):481–494. https://doi.org/10.1016/j.jcrysgro.2004.07.073
10. Galenko P.K., Ankudinov V. Local non-equilibrium effect on the growth kinetics of crystals. Acta Materialia. 2019;168: 203–209. https://doi.org/10.1016/j.actamat.2019.02.018
11. Galenko P.K., Jou D. Rapid solidification as non-ergodic phenomenon. Physics Reports. 2019;818:1–70. https://doi.org/10.1016/j.physrep.2019.06.002
12. Sobolev S.L. Local non-equilibrium diffusion model for solute trapping during rapid solidification. Acta Materialia. 2012;60(6–7):2711–2718. https://doi.org/10.1016/j.actamat.2012.01.036
13. Lipton J., Glicksman M.E., Kurz W. Dendritic growth into undercooled alloy metals. Materials Science and Engineering. 1984;65(1):57–63. http://dx.doi.org/10.1016/0025-5416(84)90199-X
14. Дрозин А.Д., Дудоров М.В., Рощин В.Е., Гамов П.А., Менихес Л.Д. Математическая модель образования кристаллических зародышей в переохлажденном расплаве эвтектического сплава. Вестник ЮУрГУ. Серия Математика. Механика. Физика. 2012;(11):66–72.
15. Dudorov M.V., Drozin A.D., Roshchin V.E., Vyatkin G.P. Nonlinear theory of the growth of new phase particles in supercooled metal melts. Russian Journal of Physical Chemistry. 2024;98:2447–2452. https://doi.org/10.1134/S0036024424701619
16. Pratap A., Lad K.N., Rao T.L.S., Majmudar P., Saxena N.S. Kinetics of crystallization of amorphous Cu50Ti50 alloy. Journal of Non-Crystalline Solids. 2004;345–346:178–181. https://doi.org/10.1016/j.jnoncrysol.2004.08.018
17. Khanolkar G.R., Rauls M.B., Kelly J.P., Graeve O.A., Hodge A.M., Eliasson V. Shock wave response of iron-based in situ metallic glass matrix composites. Scientific Reports. 2016;6(1):22568. https://doi.org/10.1038/srep22568
18. Yang C., Liu F., Yang G., Zhou Y. Structure evolution upon non-equilibrium solidification of bulk undercooled Fe–B system. Journal of Crystal Growth. 2009;311(2):404–412. https://doi.org/10.1016/j.jcrysgro.2008.11.025
19. Zhang D., Xu J., Liu F. In situ observation of the competition between metastable and stable phases in solidification of undercooled Fe-17at. pctB alloy melt. Metallurgical and Materials Transactions A. 2015;46:5232–5239. https://doi.org/10.1007/s11661-015-3104-0
20. Battezzati L., Antonione C., Baricco M. Undercooling of Ni-B and Fe-B alloys and their metastable phase diagrams. Journal of Alloys and Compounds. 1997;247(1–2):164–171. https://doi.org/10.1016/S0925-8388(96)02570-4
21. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: В 3-х томах. Т. 1. Москва: Физматлит; 2003:680.
Об авторах
А. Д. ДрозинРоссия
Александр Дмитриевич Дрозин, д.т.н., профессор, ведущий научный сотрудник НИЛ «Водородные технологии в металлургии»
Россия, 454080, Челябинск, пр. Ленина, 76
М. В. Дудоров
Россия
Максим Владимирович Дудоров, к.ф.-м.н., старший научный сотрудник НИЛ «Водородные технологии в металлургии»
Россия, 454080, Челябинск, пр. Ленина, 76
Рецензия
Для цитирования:
Дрозин А.Д., Дудоров М.В. Критерии существования локальных равновесий в переохлажденных расплавах. Известия высших учебных заведений. Черная Металлургия. 2025;68(6):607-612. https://doi.org/10.17073/0368-0797-2025-6-607-612
For citation:
Drozin A.D., Dudorov M.V. Criteria for the existence of local equilibria in supercooled melts. Izvestiya. Ferrous Metallurgy. 2025;68(6):607-612. https://doi.org/10.17073/0368-0797-2025-6-607-612
JATS XML