Теоретическая прочность аустенита при наличии в кристалле поры или вакансий: молекулярно-динамическое исследование

Введение

При пластической деформации в качестве источников дислокаций в поликристаллических материалах помимо границ раздела (границ зерен и их тройных стыков, межфазных границ, поверхностей) важную роль играют поры и микропустоты [1 ‒ 3]. Однако работ, посвященных исследованию механизмов пластической деформации на атомном уровне с участием пор, сравнительно немного. К настоящему времени с помощью компьютерного моделирования показано, что испускание дислокаций порами при деформации происходит за счет формирования дислокационных петель [3 ‒ 6], причем авторы работ [5; 6] утверждают, что в ГЦК кристаллах при этом петли формируются одновременно в двух плоскостях скольжения. С увеличением размера поры уменьшается критическое напряжение, при котором происходит образование дислокации [5; 6].

Точечные дефекты, например решеточные вакансии, также, очевидно, приводят к снижению теоретической прочности, однако влияние их концентрации на прочность изучено недостаточно, особенно в сравнении с влиянием их скоплений, в частности, пор. Настоящая работа посвящена сравнительному исследованию методом молекулярной динамики влияния вакансий и поры на теоретическую прочность аустенита в зависимости от температуры и концентрации вакансий или размера поры. Интерес к аустениту вызван тем, что он является основой многих сталей, имеющих большое практическое значение, например, стали Гадфильда [7; 8]. Кроме того, качественные результаты, полученные для аустенита в настоящей работе, очевидно, можно будет распространить на другие металлы с ГЦК кристаллической решеткой.

Ранее [9] методом молекулярной динамики было проведено исследование скорости скольжения краевой и винтовой дислокаций в аустените и стали Гадфильда в зависимости от температуры и скорости деформирования. Была рассчитана энергия образования рассматриваемых дислокаций. Настоящее исследование является продолжением работы [9].

Описание модели

Расчетная ячейка аустенита в молекулярно-динамической модели имела форму прямоугольного параллелепипеда (рис. 1) длиной 14,0 нм, высотой 14,0 нм и шириной 5,1 нм. Количество атомов изначально составляло 87 040. Ориентация координатных осей соответствовала следующим кристаллографическим направлениям в ГЦК решетке: x – [\(\bar 1 10\)], y – [\(\bar 1\bar 12\)], z – [111]. В работе рассматривался сдвиг вдоль двух направлений: оси y (как показано на рис. 1) и оси z. Сдвиг в модели инициировался путем смещения атомов в приграничных областях (на рис. 1 выделены темно-серым цветом). Атомы в этих областях на противоположных сторонах расчетной ячейки в процессе компьютерного эксперимента перемещались в противоположных направлениях с постоянной скоростью 20 м/с. В работе [9] при моделировании особенностей скольжения дислокации в аустените это значение было выбрано как оптимальное для моделирования сдвига методом молекулярной динамики. Движение остальных атомов в расчетной ячейке никак не ограничивалось, оно описывалось классическими уравнениями движения Ньютона. Граничные условия вдоль остальных осей использовались периодические.

Для описания межатомных взаимодействий в аустените использовался ЕАМ потенциал Лау [10], хорошо воспроизводящий структурные, энергетические и упругие характеристики аустенита [10; 11]. Шаг интегрирования по времени в методе молекулярной динамики составлял 2 фс [12 ‒ 14]. Температуру задавали через начальные скорости атомов согласно распределению Максвелла. При задании температуры обязательным являлся учет теплового расширения кристаллической решетки [13 ‒ 15]. Для используемого в работе потенциала межатомного взаимодействия коэффициент теплового расширения равен 18·10\(^–\)⁶ К\(^–\)¹, что хорошо согласуется со справочными данными [11]. Для сохранения температуры постоянной в процессе моделирования использовался термостат Нозе-Гувера. На всем интервале варьирования температуры (от 100 до 1500 К) тип кристаллической решетки ГЦК сохранялся постоянным, полиморфное превращение в настоящей работе не учитывалось.

Пора создавалась в центре расчетной ячейки путем удаления атомов в сферической области. Диаметр поры варьировался в пределах 0,6 – 2,0 нм. Вакансии вводились путем удаления случайных атомов по всему объему расчетной ячейки, кроме приграничных слоев (на рис. 1 выделены темно-серым). Рассматриваемые значения концентрации вакансий соответствовали количеству удаленных атомов при создании пор. После введения дефектов следовала процедура релаксации структуры до достижения равновесного состояния.

Результаты и обсуждение

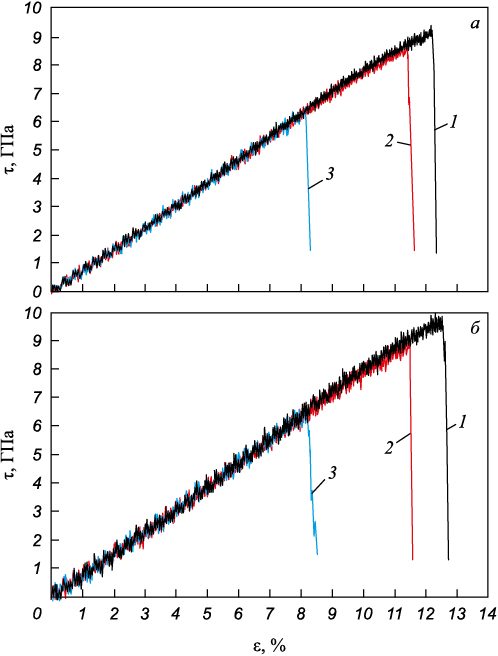
На рис. 2 изображены зависимости напряжение – деформация для двух рассматриваемых ориентаций сдвига с постоянной скоростью 20 м/с при температуре 300 К для бездефектного кристалла (1), кристалла, содержащего 79 случайно разбросанных по объему вакансий (2), и кристалла, содержащего пору диаметром 1,2 нм (3). Количество вакансий было равно количеству удаленных атомов при создании рассматриваемой поры и соответствовало в данном случае концентрации 0,09 %.

Теоретическая прочность кристаллов металлов на сдвиг, как известно, очень высока и может достигать более 10 ГПа [1; 5; 6; 16; 17]. Введение всего одной дислокации в чистый кристалл в молекулярно-динамической модели снижает прочность до нескольких сотен МПа [18]. Как видно из рис. 2, пластическая деформация в чистом кристалле аустенита при температуре 300 К начиналась при сдвиге как вдоль оси y, так и вдоль оси z, примерно при том же значении деформации (12,0 ‒ 12,5 %) и напряжения (9,0 ‒ 9,5 ГПа). Следует подчеркнуть, что идеальный кристалл изначально не содержал каких-либо источников образования дислокаций, даже свободной поверхности. В связи с этим область упругой деформации была сравнительно очень большой.

В отсутствие источников дислокаций пластическая деформация осуществлялась путем формирования дислокационных диполей (дислокаций с противоположными векторами Бюргерса). Полные дислокации сразу формировались в виде пары частичных дислокаций Шокли, разделенных дефектом упаковки. Расстояние между частичными дислокациями, как правило, составляло несколько нанометров, что согласуется с результатами моделирования других авторов [19 – 21]. Наряду с дислокационными диполями, при дальнейшей деформации интенсивно проходил также процесс образования деформационных двойников.

Как можно видеть на рис. 2, наличие поры диаметром 1,2 нм существенно снижает теоретическую прочность: пластический сдвиг и образование дислокаций происходят при существенно более низких значениях деформации и напряжения (примерно 8,5 % и 6 ГПа соответственно). При этом случайно разбросанные по объему расчетной ячейки вакансии при том же количестве, что и в поре, влияют на предел прочности значительно слабее, однако, что является интересным результатом, все же снижают его: дислокации образуются при деформации примерно 11,5 % и напряжении 8,5 ГПа. Таким образом, даже простые точечные дефекты (вроде вакансий) снижают теоретическую прочность кристалла.

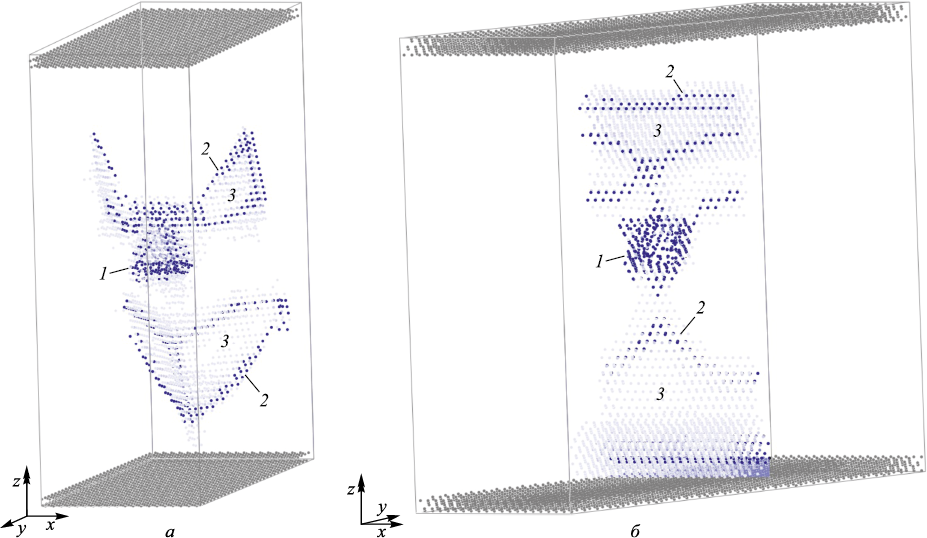
Испускание дислокаций порой при деформации происходило путем формирования дислокационных петель, что согласуется с результатами моделирования других авторов [3 ‒ 6]. Примеры образования подобных петель из поры диаметром 1,2 нм при сдвиге вдоль осей y и z приведены на рис. 3. Можно видеть, что петли формируются в двух плоскостях скольжения, на что указывали также авторы работ [5; 6]. Для изображения дислокаций в расчетной ячейке использовался визуализатор среднего расстояния до ближайших атомов (дает представление о наличии локального растяжения и косвенно о распределении свободного объема). Для каждого атома проводили расчет среднего расстояния до ближайших атомов. Если среднее расстояние незначительно отличалось от расстояния, соответствующего идеальному кристаллу, атом не выделяли цветом; в противном случае атом закрашивали в тот или иной оттенок.

Температура, как известно, влияет на упругие свойства материала и вероятность образования дислокаций при деформации. Модули упругости в широком диапазоне температур уменьшаются с ростом температуры почти линейно [22 – 24], что обычно связывают с тепловым расширением [22]. Пластическая деформация с ростом температуры в большинстве материалов начинается при меньших значениях напряжения [24 – 26].

На рис. 4 изображены зависимости предельной прочности от температуры при сдвиге вдоль осей y и z. Зависимости приведены для бездефектного кристалла (1), кристалла, содержащего 79 случайно разбросанных по объему вакансий (2), и кристалла, содержащего пору диаметром 1,2 нм (3). Во всех случаях с ростом температуры действительно прочность падает. При этом следует отметить важную особенность: при повышении температуры степень влияния дефектов на теоретическую прочность снижается. Отличия значений предельной прочности для случаев с бездефектным кристаллом, с вакансиями и порой уменьшаются с ростом температуры, стремясь к одному значению (пересечения зависимостей, видимо, следует ожидать при температуре плавления).

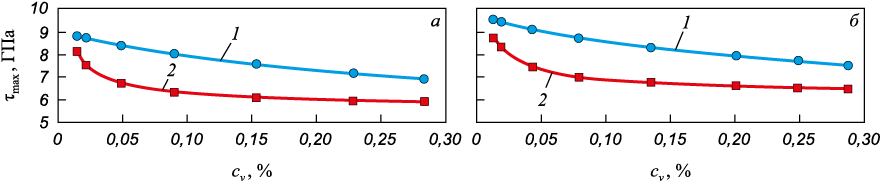
На рис. 5 изображены зависимости предельной прочности при температуре 300 К при сдвиге вдоль осей y и z (рис. 5, б) от количества (%) удаленных из расчетной ячейки атомов с_v в виде отдельных случайно разбросанных вакансий или пор (зависимости 1 и 2 соответственно на рис. 2, 4). Для сравнения: при диаметре поры 1,0 нм с_v = 0,05 %, при диаметре поры 1,2 нм с_v = 0,09 %, при диаметре 1,6 нм с_v = 0,23 %.

Как можно видеть, с ростом как концентрации вакансий, так и радиуса пор прочность снижается. При этом наиболее сильная зависимость наблюдается для малых размеров пор: примерно до 1 нм. При дальнейшем увеличении радиуса поры прочность продолжает снижаться, но гораздо слабее, чем при малых размерах поры. Влияние концентрации вакансий в рассматриваемом диапазоне на теоретическую прочность более плавное и почти линейное.

Выводы

Методом молекулярной динамики проведено исследование влияния поры разного диаметра, а также соответствующей концентрации отдельных вакансий на теоретическую прочность аустенита при разной температуре. Деформация в модели осуществлялась путем сдвига с постоянной скоростью 20 м/с. Рассматривался сдвиг вдоль двух направлений: [\(\bar 1\bar 12\)] и [111]. Зависимости напряжение – деформация, полученные для обоих направлений сдвига, имели аналогичный вид. В отсутствие источников дислокаций пластическая деформация осуществлялась путем формирования дислокационных диполей (дислокаций с противоположными векторами Бюргерса). Наличие поры существенно снижало предельную прочность аустенита. Обнаружено, что случайно разбросанные по объему расчетной ячейки одиночные вакансии также приводят к снижению предельной прочности, но, естественно, не так сильно, как пора. Испускание дислокаций порой при деформации происходило путем формирования дислокационных петель, как правило, сразу в двух плоскостях скольжения. Сильнее влияние поры и вакансий на предельную прочность наблюдалось при низких температурах. При увеличении температуры влияние дефектов на критическое напряжение, при котором происходило образование дислокаций, снижалось. С увеличением размера поры, как и концентрации вакансий, прочность уменьшалась. При этом наиболее сильная зависимость наблюдалась для пор диаметром до 1 нм. Влияние концентрации вакансий в рассматриваемом диапазоне на предельную прочность оказалось сравнительно более плавное и почти линейное.