Theoretical strength of austenite in the presence of a pore or vacancies in the crystal: Molecular dynamics study

Introduction

During plastic deformation, in addition to interface boundaries (such as grain boundaries and their triple junctions, interphase boundaries, and surfaces), pores and microvoids play crucial role as sources of dislocations in polycrystalline materials [1 – 3]. However, there has been relatively little research dedicated to studying the mechanisms of plastic deformation at the atomic level involving pores. To date, computer modeling has demonstrated that dislocation emission from pores during deformation is facilitated by the formation of dislocation loops [3 – 6]. The authors of [5; 6] assert that in FCC crystals, loops are formed simultaneously in two slip planes. Moreover, as the pore size increases, the critical stress required for dislocation formation decreases [5; 6].

Point defects, for example, vacancies, also contribute significantly to a decrease in theoretical strength, yet the impact of their concentration on strength remains insufficiently explored, especially when compared to the effect of pore accumulations. The present study focuses on conducting a comparative analysis using molecular dynamics to investigate the influence of vacancies and pores on the theoretical strength of austenite, with consideration given to variations in temperature and vacancy concentration or pore size. Austenite garners particular interest as it serves as the foundation for many steels of considerable practical importance, such as Hadfield steel [7; 8]. Furthermore, the qualitative findings derived for austenite in this study can readily be extrapolated to other metals possessing an FCC crystal lattice.

Previously, in [9], the molecular dynamics method was employed to examine the slip velocity of edge and screw dislocations in austenite and Hadfield steel, contingent upon temperature and strain rate. The energy of formation for the aforementioned dislocations was also computed. This investigation serves as a continuation of the research documented in [9].

Model description

In the molecular dynamics model, the calculation cell representing austenite had the shape of a rectangular parallelepiped (see Fig. 1) with dimensions of 14.0 nm in length, 14.0 nm in height, and 5.1 nm in width. Initially, the cell contained 87,040 atoms. The orientation of the coordinate axes corresponded to specific crystallographic directions within the FCC lattice: x – [\(\bar 1 10\)], y – [\(\bar 1\bar 12\)], z – [111]. The study investigated shear deformation along two directions: the y-axis (Fig. 1) and the z-axis. To induce shear in the model, atoms in the boundary regions (highlighted in dark gray in Fig. 1) were displaced. Atoms on opposite sides of the calculation cell moved in opposite directions at a constant speed of 20 m/s during the computer experiment. In previous research [9], this velocity was determined as optimal for modeling shear using the molecular dynamics method in austenite. The motion of the remaining atoms within the computational cell was unrestricted and governed by Newton’s classical equations of motion. Boundary conditions along the other axes were set as periodic.

Interatomic interactions in austenite were described using Lau’s Embedded Atom Method (EAM) potential [10], known for accurately reproducing the structural, energetic, and elastic properties of austenite [10; 11]. The time integration step in the molecular dynamics method was set to 2 fs [12 – 14]. The initial velocities of atoms were assigned according to the Maxwell distribution to achieve the desired temperature. It was essential to consider the thermal expansion of the crystal lattice when setting the temperature [13 – 15]. The interatomic interaction potential employed in this study has a thermal expansion coefficient of 18·10\(^–\)⁶ K\(^–\)¹, aligning well with reference data [11]. To maintain a constant temperature throughout the modeling, a Nosé–Hoover thermostat was utilized. Throughout the temperature range explored (from 100 to 1500 K), the FCC crystal lattice type remained consistent; polymorphic transformations were not considered in this investigation.

A pore was created in the center of the computational cell by removing atoms in a spherical region. The pore diameter varied from 0.6 to 2.0 nm. Vacancies were introduced by removing random atoms throughout the entire volume of the computational cell, except for the boundary layers (shown in dark gray in Fig. 1). The considered values of vacancy concentration corresponded to the number of removed atoms during the creation of pores. After the introduction of defects, a procedure of relaxation of the structure followed until an equilibrium state was achieved.

Results and discussion

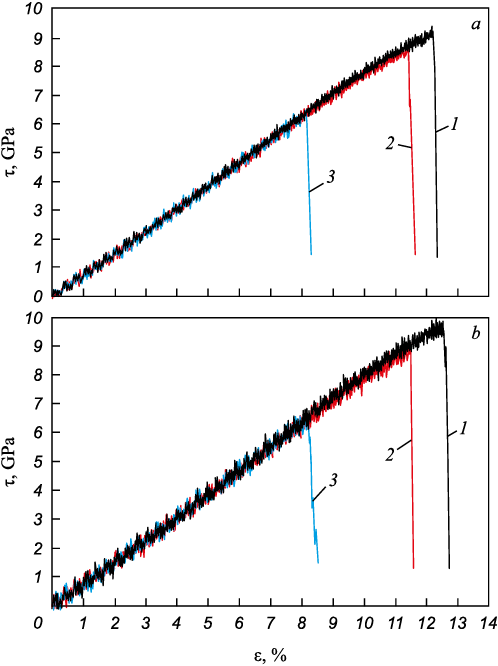
Fig. 2 depicts the stress–strain dependences for the two shear orientations considered, with a constant speed of 20 m/s at a temperature of 300 K, for three scenarios: a defect-free crystal (1), a crystal containing 79 vacancies randomly distributed throughout its volume (2), and a crystal containing a pore with a diameter of 1.2 nm (3). The number of vacancies equaled the number of atoms removed during creation of the aforementioned pore resulting in a concentration of 0.09 % in this case.

It is widely acknowledged that the theoretical shear strength of metal crystals is exceptionally high, often exceeding 10 GPa [1; 5; 6; 16; 17]. However, introducing just one dislocation into a pristine crystal in the molecular dynamics model reduces the strength to several hundred MPa [18]. As illustrated in Fig. 2, plastic deformation in a pure austenite crystal at 300 K commenced with shear along both the y and z axes at approximately the same strain values (12.0 – 12.5 %) and stress levels (9.0 – 9.5 GPa). It is crucial to highlight that the initial ideal crystal lacked any sources of dislocation formation, including free surfaces. Consequently, the region of elastic deformation was relatively extensive.

In the absence of dislocation sources, plastic deformation occurred through the creation of dislocation dipoles, consisting of dislocations with opposite Burgers vectors. Complete dislocations promptly emerged as pairs of partial Shockley dislocations separated by a stacking fault. Typically, the distance between partial dislocations was a few nanometers, consistent with modeling findings reported by other researchers [19 – 21]. Additionally, alongside dislocation dipoles, the formation of deformation twins was also prominent during subsequent deformation stages.

As illustrated in Fig. 2, the inclusion of a pore with a diameter of 1.2 nm notably diminishes the theoretical strength: plastic shear and dislocation formation occur at significantly lower strain and stress thresholds (approximately 8.5 % and 6 GPa, respectively). Conversely, vacancies randomly distributed throughout the computational cell, equating in number to those in the pore, exert a comparatively weaker influence on the ultimate strength. However, intriguingly, they still contribute to its reduction, with dislocations forming at a strain of about 11.5 % and a stress of 8.5 GPa. Thus, even basic point defects like vacancies attenuate the theoretical strength of the crystal.

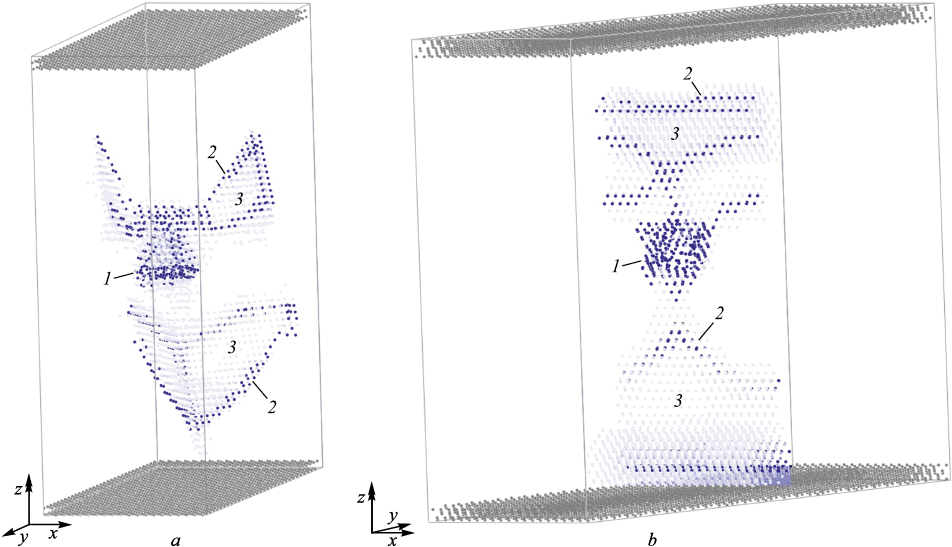
Dislocation emission from a pore during deformation transpired via the formation of dislocation loops, aligning with findings from modeling conducted by other researchers [3 – 6]. Fig. 3 depicts examples of such loop formation from a pore with a diameter of 1.2 nm upon displacement along the y and z axes. It is evident that loops manifest in two slip planes, consistent with observations made by authors elsewhere [5; 6]. To visualize dislocations within the computational cell, an average distance to the nearest atoms visualizer was utilized, providing insight into local stretching and indirectly indicating the distribution of free volume. For each atom, the average distance to the nearest atoms was computed. If this distance deviated slightly from the distance corresponding to an ideal crystal, the atom remained uncolored; otherwise, it was assigned a color based on the deviation.

As commonly understood, temperature significantly impacts the elastic properties of materials and the likelihood of dislocation formation during deformation. Elastic moduli typically decrease nearly linearly with rising temperatures across a wide range [22 – 24], a trend often attributed to thermal expansion [22]. Plastic deformation in most materials initiates at lower stress levels as temperature increases [24 – 26].

Fig. 4 illustrates the temperature dependence of ultimate strength for shear along the y and z axes. The dependencies are presented for a defect-free crystal (1), a crystal containing 79 randomly scattered vacancies (2), and a crystal with a pore diameter of 1.2 nm (3). In all instances, strength diminishes with increasing temperature. Notably, as temperature rises, the influence of defects on theoretical strength diminishes. Specifically, the discrepancies in ultimate strength values between the defect-free crystal and those with vacancies or pores decrease with increasing temperature, converging toward the same value. It is pertinent to note that this convergence suggests an anticipated intersection of dependencies at the melting temperature.

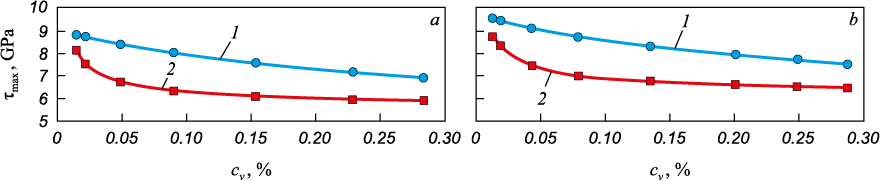
Fig. 5 presents the dependencies of ultimate strength at a temperature of 300 K for shear along the y and z axes (Fig. 5, b) concerning the percentage of atoms c_v removed from the calculation cell in the form of individual randomly scattered vacancies or pores (designated as dependencies 1 and 2, respectively, in Fig. 2, 4). For comparison, with a pore diameter of 1.0 nm, с_v = 0.05 %; with a pore diameter of 1.2 nm, с_v = 0.09 %; and with a pore diameter of 1.6 nm, с_v = 0.23 %.

As evident, an increase in both vacancy concentration and pore radius correlates with a reduction in strength. Notably, the most pronounced dependence is observed for small pore sizes, up to approximately 1 nm. Beyond this range, while strength continues to decrease with increasing pore radius, the rate of decline is notably less pronounced compared to smaller pore sizes. Conversely, the influence of vacancy concentration within the considered range on theoretical strength is more gradual and nearly linear.

Conclusions

The influence of pores of varying diameters, along with the corresponding concentration of individual vacancies, on the theoretical strength of austenite across different temperatures was investigated using the molecular dynamics method. Deformation in the model was induced by shearing at a constant speed of 20 m/s, considering shifts along two directions: [\(\bar 1\bar 12\)] and [111]. Stress-strain dependences obtained for both shear directions exhibited similar trends. In the absence of dislocation sources, plastic deformation ensued through the formation of dislocation dipoles characterized by dislocations with opposite Burgers vectors. The presence of pores substantially reduced the ultimate strength of austenite, while single vacancies randomly dispersed throughout the computational cell also contributed to a decrease in ultimate strength, albeit to a lesser extent compared to pores. Dislocation emission from pores during deformation occurred through the formation of dislocation loops, typically manifesting in two slip planes simultaneously. A more pronounced impact of pores and vacancies on ultimate strength was observed at lower temperatures. However, as temperature increased, the influence of defects on the critical stress at which dislocation formation occurred diminished. Moreover, with increasing pore size and vacancy concentration, the strength exhibited a decreasing trend. Notably, the strongest dependence was observed for pores with diameters up to 1 nm. The effect of vacancy concentration within the considered range on ultimate strength was relatively smoother and displayed an almost linear behavior.