Перейти к:
Математическая модель состояния горна доменной печи на основе показаний термопар, находящихся в поясах холодильников
https://doi.org/10.17073/0368-0797-2025-3-316-323
Аннотация
Контроль футеровки горна доменной печи является важным аспектом в обеспечении эффективной и безопасной работы доменного производства. Футеровка горна играет ключевую роль в защите стен доменной печи от воздействия высоких температур и химически агрессивного шлакового расплава. Раннее выявление зон повышенного износа позволяет планировать профилактические работы, минимизируя простои и потери производительности. Более того, это способствует эффективному расходованию ресурсов, так как позволяет оптимизировать замену поврежденных участков футеровки, избегая излишних затрат на превентивные меры. В работе приведено описание разработанной трехмерной нестационарной модели горна доменной печи, базирующейся на показаниях термопар. Модель позволяет оценить форму разгара горна и распределение температур в кладке горна в трехмерной и двумерной (графической) формах. Для оценки разгара футеровки горна использованы показания термопар, установленных в районе трех нижних поясов холодильников. Указанная математическая модель может быть внедрена в доменный процесс в любое время после капитального ремонта I разряда. В случае, если прошло достаточно много времени после задувки доменной печи и в футеровке горна возможно образование разгара или гарнисажа, необходимо также использовать результаты ультразвукового контроля нижней части доменной печи. Математическая модель состояния горна доменной печи позволяет принимать пользователю обоснованные решения по предотвращению аварийных ситуаций, связанных с прогаром футеровки, и является перспективным инструментом для повышения эффективности и безопасной эксплуатации доменных печей.
Ключевые слова
Для цитирования:
Дмитриев А.Н., Витькин Д.А., Золотых М.О., Витькина Г.Ю. Математическая модель состояния горна доменной печи на основе показаний термопар, находящихся в поясах холодильников. Известия высших учебных заведений. Черная Металлургия. 2025;68(3):316-323. https://doi.org/10.17073/0368-0797-2025-3-316-323
For citation:
Dmitriev A.N., Vit’kin D.A., Zolotykh M.O., Vit’kina G.Yu. Mathematical model of blast furnace hearth condition based on data from thermocouples in refrigerator belts. Izvestiya. Ferrous Metallurgy. 2025;68(3):316-323. https://doi.org/10.17073/0368-0797-2025-3-316-323
Введение
Эффективный контроль разгара футеровки горна доменной печи (ДП) является неотъемлемой частью комплексной системы управления доменным производством, направленной на достижение высоких технико-экономических показателей.
Для контроля разгара футеровки горна ДП существует несколько способов:
– принципы системного анализа и решение прямой и обратной задач контроля тепловой работы ДП [1 – 3];
– систематическая диагностика состояния футеровки горна с использованием разработанного на фирме метода отраженного акустико-ультразвукового сигнала AU-E [4];
– метод группового учета аргументов, основным параметром в котором для оценки теплового состояния низа ДП принято содержание кремния в чугуне [5];
– оценка среднего теплового потока охлаждающей воды в холодильниках [6; 7];
– учет взаимосвязи между конструкцией футеровки горна и износом футеровки [8 – 10].
Одним из наиболее достоверных является способ, включающий в процессе капитального ремонта установку специальных термопар в определенном количестве и в определенных точках, что в дальнейшем позволит контролировать толщину футеровочных слоев и оценивать градиент температур в кладке [11 – 14]. Расчет остаточной толщины футеровки горна и лещади, а также их двух- и трехмерная визуализации осуществляются как с помощью известных программных пакетов (например, Matlab [15]), так и оригинальных программ [16 – 18]. Наиболее наглядным для моделирования теплового потока может считаться метод конечных элементов [19; 20].
Контроль состояния огнеупорной футеровки горна с использованием математической модели [21] возможен после задувки ДП и выхода ее теплового состояния на стационарный режим. Рассматриваемая в настоящей работе математическая модель может использоваться в любое время после капитального ремонта I разряда. В случае, если прошло достаточно много времени после задувки, в футеровке горна возможно образование разгара или гарнисажа. Тогда необходимо использовать результаты ультразвукового контроля (УЗК) нижней части ДП.
Исходные данные
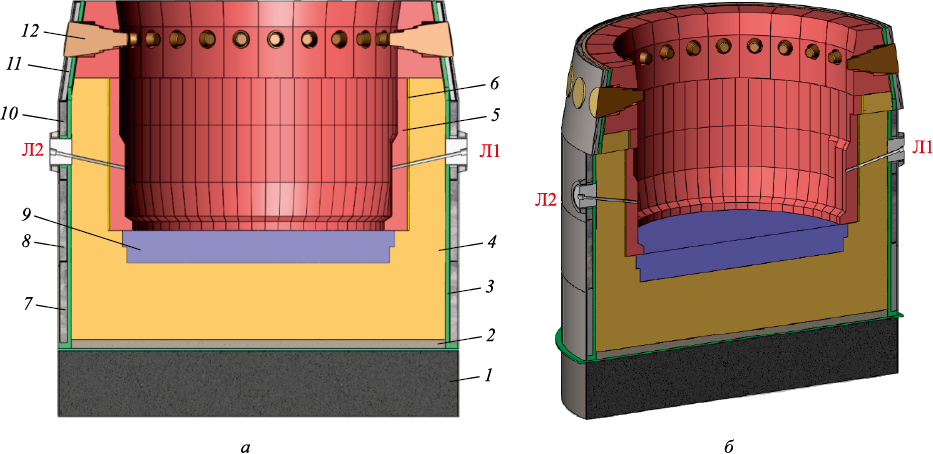
На рис. 1 представлен вертикальный разрез горна ДП объемом 2000 м3. Видно, что первый пояс холодильников охватывает большую часть лещади, а второй и третий расположены в зоне металлоприемника ДП.
Рис. 1. Вертикальный разрез горна доменной печи, включая лещадь: |
Перед тремя поясами холодильников горна и лещади установлены термопары (20 шт. на каждом поясе). Для оценки разгара горна могут быть использованы данные с указанных термопар, которые имеются в базе данных АСУ ТП ДП (дискретность съема может составлять от 1 мин). Введено понятие эталонных температур термопар (ЭТТ) – это температуры с термопар, снятые в момент проведения УЗК разгара горна, результатом которого явились данные о толщине всех слоев футеровки на четырех горизонтах. В результате проведенного УЗК горна ДП устанавливается, что в поясе горна наблюдается износ керамических и углеродистых блоков, а также наличие гарнисажа. Горизонтальные разрезы выполнены на высоте 6,5; 7,3; 7,9; 9,9 м.
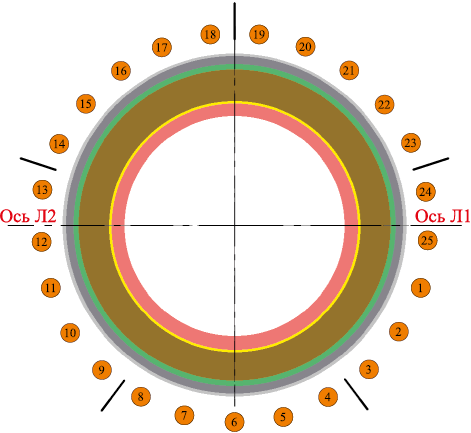
На рис. 2 приведен горизонтальный разрез горна с привязкой к фурменным приборам и леткам. Начало цилиндрической системы координат поместили в центр лещади на отметке 0. За начало отчета принята ось фурменного прибора 1 (рис. 2) и далее по часовой стрелке через равный угол. В данном случае высота будет постоянна и равна отметке секущей плоскости.
Рис. 2. Горизонтальный разрез горна с привязкой |
Таким образом, имеются четыре секущих плоскости, которые определяют геометрию гарнисажа. При помощи CAD системы можно получить максимально точную 3D модель гарнисажа в горне.
В расчетную область задачи входят зона боковых стенок горна и зона лещади, где теплообмен описывается уравнением теплопроводности в твердом материале. Начальными условиями выступают известные данные последнего УЗК (эталонные температуры). Внутренней границей является поверхность контакта между расплавленным металлом и футеровкой (гарнисажем). Температура внутренней поверхности футеровки принимается равной значению текущей температуры чугуна, измеренной термопарами, установленными в летке ДП, либо, при отсутствии термопар, задается оператором (например, 1450 °С). Внешней границей является значение температур по данным термопар в поясе холодильников. Допущено, что температура охлаждающего агента в холодильниках постоянна. Для упрощения расчета предположен идеальный тепловой контакт между слоями футеровки. В областях сопряжения теплофизические характеристики материалов усредняются.
Расчет теплопроводности через многослойную цилиндрическую стенку
Расчет линейной плотности теплового потока через цилиндрическую стенку выполняли по формулам (1) – (3)
| \[\begin{array}{c}q = \frac{{\pi ({T_1} - {T_2})}}{{\frac{1}{{{\alpha _1}{d_1}}} + \frac{1}{{2\lambda }}\ln \frac{{{d_2}}}{{{d_1}}} + \frac{1}{{{\alpha _2}{d_2}}}}} = \\ = {k_l}\pi ({T_2} - {T_1}) = \frac{{\pi ({T_2} - {T_1})}}{{{R_1}}};\end{array}\] | (1) |
| \[{k_l} = \frac{1}{{\frac{1}{{{\alpha _1}{d_1}}} + \frac{1}{{2\lambda }}\ln \frac{{{d_2}}}{{{d_1}}} + \frac{1}{{{\alpha _2}{d_2}}}}};\] | (2) |
| \[{R_1} = \frac{1}{{{\alpha _1}{d_1}}} + \frac{1}{{2\lambda }}\ln \frac{{{d_2}}}{{{d_1}}} + \frac{1}{{{\alpha _2}{d_2}}},\] | (3) |
где T1 и T2 – температура горячего и холодного флюидов, °С (К); α1 , α2 – коэффициенты теплоотдачи от горячего флюида к стенке и от стенки к холодному флюиду, Вт/(м2·К); d1 и d2 – внутренний и наружный диаметры цилиндрической стенки, м; λ – коэффициент теплопроводности стенки, Вт/(м·К); kl – линейный коэффициент теплопередачи через цилиндрическую стенку, Вт/(м·К); R1 – линейное термическое сопротивление теплопередачи через стенку цилиндрической формы, (м·К)/Вт.
Линейную плотность теплового потока при теплопередаче через цилиндрическую стенку, состоящую из n слоев разной толщины и с разными физическими свойствами, рассчитывали по формуле (4)
| \[q = \frac{{\pi ({T_1} - {T_2})}}{{\frac{1}{{{\alpha _1}{d_1}}} + \sum\limits_{i = 1}^n {\frac{1}{{2{\lambda _i}}}\ln \frac{{{d_{i + 1}}}}{{{d_i}}} + \frac{1}{{{\alpha _2}{d_{n + 1}}}}} }},\] | (4) |
где λi – коэффициент теплопроводности i-го слоя, Вт/(м·К); di и di + 1 – внутренний и наружный диаметры i-го слоя цилиндрической стенки, м.
Для этого случая теплопередачи через цилиндрическую стенку линейное термическое сопротивление равно
| \[{R_l} = \frac{1}{{{\alpha _1}{d_1}}} + \sum\limits_{i = 1}^n {\frac{1}{{2{\lambda _i}}}\ln \frac{{{d_{i + 1}}}}{{{d_i}}} + \frac{1}{{{\alpha _2}{d_{n + 1}}}}} .\] | (5) |
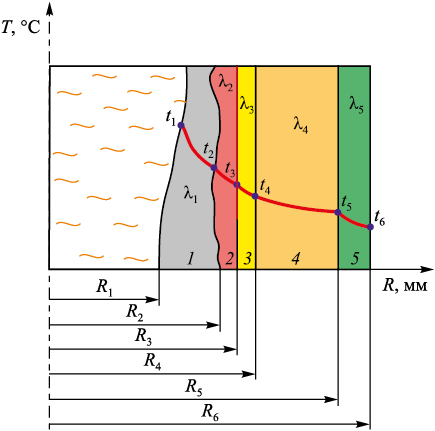
Расчет процесса теплопередачи через пятислойную стенку производили для четырех заданных горизонтов с известными толщинами слоев (например, для области, которую охватывает второй пояс холодильников эти слои указаны на рис. 3).
Рис. 3. Слои изоляционных материалов в области второго пояса холодильников: |
Поскольку имеет место разрушение керамического стакана и изоляционного материала, их толщины будут отличаться от исходных условий в рассматриваемом секторе контроля температуры (СКТ). Высота СКТ равна высоте холодильника. Если провести горизонтальные сечения вдоль СКТ, очевидно, что в каждой точке сечения температура огнеупорных материалов будет разная, а значит и разная глубина разрушения кладки (или толщина гарнисажа). Сектора контроля температуры разделены на равные части по высоте. В каждой секущей плоскости определены толщины всех слоев огнеупорных материалов, далее рассчитаны температуры в плоскости. Зная значение температуры, пропорционально определено, как будут вести себя соответствующие слои при повышении/снижении общей температуры.
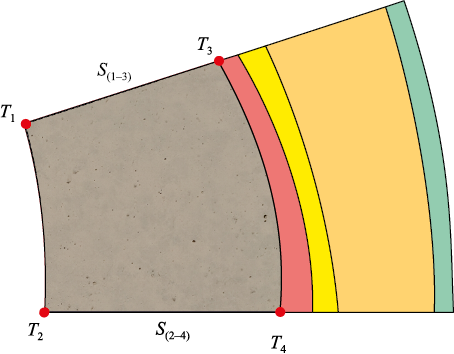
Рассмотрим сечение, например, на высоте 6,5 м (рис. 4). Толщина гарнисажа различна в радиальном направлении (от S(2–4) до S(1–3) ). Возможно изменение координат точек T1 и Т2 в следующих случаях:
– толщина гарнисажа увеличивается (T1 и Т2 стремятся к центру ДП, температура в рассматриваемом секторе снижается);
– толщина гарнисажа уменьшается (T1 и Т2 стремятся к T3 и Т4 соответственно, температура будет расти).
Рис. 4. Сектор контроля температуры в плоскости 6,5 м (вид снизу) |
По данным температурам термопар в день проведения УЗК могут быть определены эталонные распределения температур в кладке горна на всех уровнях.
Коэффициент теплопроводности гарнисажа зависит от многих условий, среди которых есть плотность гарнисажа [22]. Принято λг = 0,36 Вт/(м·°С).
В таблице приведены исходные данные для расчета процесса теплопередачи.
Исходные данные для расчета
| |||||||||||||||||||||||||||||||||||||||
Расчет теплопроводности через многослойную
плоскую стенку
Лещадь анализируемой ДП состоит из семи плотно прилегающих друг к другу слоев. Для области, которую охватывает первый пояс холодильников, эти слои следующие (от внутреннего слоя к наружному): гарнисаж; керамический слой; супермикропористые углеродистые блоки; углеродистые блоки; графитовые блоки; набивная паста; воздушное охлаждение лещади (имеются термопары).
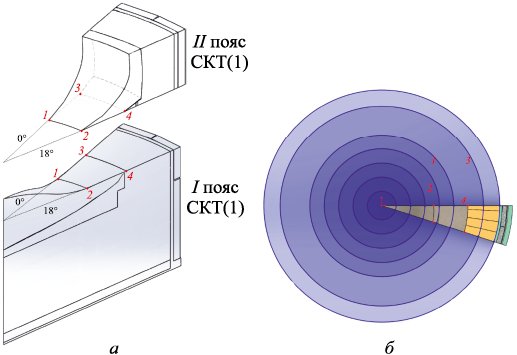
Первый пояс холодильников разделен на 20 одинаковых плоскостей (рис. 5, а). Секторы представлены на рис. 5, б.
Рис. 5. Сечение секущими цилиндрическими плоскостями (а) |
Расчет теплопередачи через плоскую стенку выполнен с использованием поверхностной плотности теплового потока, которая, как известно, связана с тепловым потоком соотношением q = Q/F, где F – площадь поверхности теплообмена.
Для стенки, состоящей из n слоев, формула расчета теплопередачи через плоскую стенку имеет вид
| \[q = \frac{{{T_1} - {T_2}}}{{\frac{1}{{{\alpha _1}}} + \sum\limits_{i = 1}^n {\frac{{{\delta _i}}}{{{\lambda _i}}} + \frac{1}{{{\alpha _2}}}} }},\] | (6) |
где δi и λi – толщина и коэффициент теплопроводности i-го слоя стенки; Rt – термическое сопротивление теплопередачи многослойной стенки, (м2·К)/Вт.
Тогда
| \[{R_t} = \frac{1}{{{\alpha _1}}} + \sum\limits_{i = 1}^n {\frac{{{\delta _i}}}{{{\lambda _i}}} + \frac{1}{{{\alpha _2}}}} ;\] | (7) |
| \[q = \frac{{{T_1} - {T_2}}}{{{R_t}}} = \frac{{\sum\limits_{i = 1}^k {\Delta {T_i}} }}{{\sum\limits_{i = 1}^k {{R_{ti}}} }} = {\rm{const}},\] | (8) |
где ΔTi – перепад температур на i-ом участке теплопередачи, °С (К); Rti – термическое сопротивление i-го участка теплопередачи, (м2·К)/Вт; k – число участков теплопередачи.
Визуализация горна и лещади ДП
Двух- и трехмерная модели горна ДП визуализируются с помощью Visualization Toolkit (VTK) открытой библиотеки для моделирования, обработки изображений и прикладной визуализации, на C++.
Трехмерные объекты задаются наборами вершин и граней, проходящих через эти вершины. Данные модели являются квазителами вращения, поэтому координаты вершин задаются в цилиндрической системе координат. Центр этой системы отчета лежит на мнимой оси, проходящей вертикально через центр печи, начиная с отметки 0. В свою очередь VTK принимает координаты вершин фигур в прямоугольных координатах X, Y, Z. Для преобразования координат используются формулы: X = R cos(A); Y = R sin(A); Z = H.
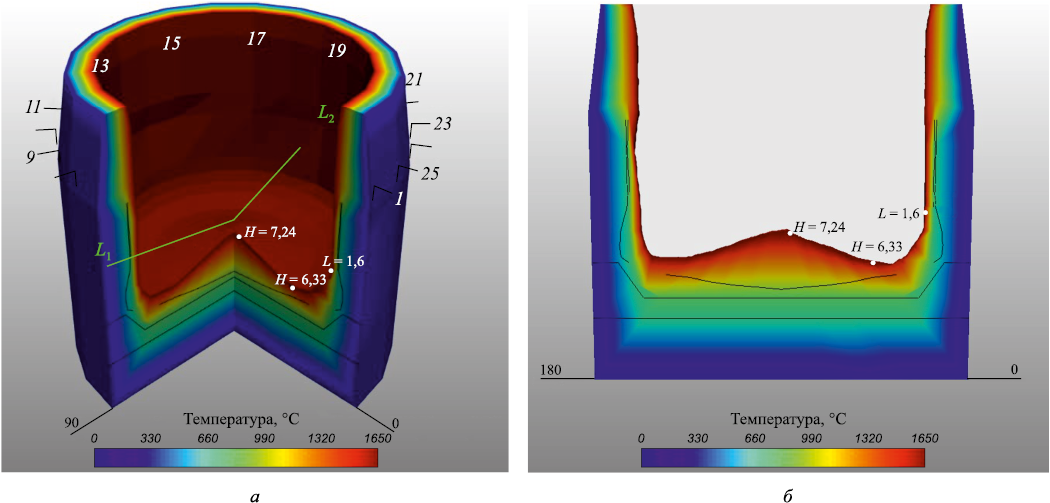
Координаты вершин на внешней поверхности печи являются константами, заданными на этапе разработки модели. Координаты вершин на внутренней поверхности печи меняются в зависимости от толщины футеровки, вычисленной по математической модели разгара горна. Цвет отображения кладки представляет собой цветовой градиент, соответствующий температуре футеровки (рис. 6).
Рис. 6. 3D модель горна и лещади (температурное распределение) (а); |
Для наглядности отображения в трехмерном представлении горна может быть вырезан любой сектор. Это позволяет оценить внутреннее состояние стенки, при этом азимуты, по которым производится сечение могут быть заданы произвольно, что позволяет контролировать весь объем кладки. Торцы сечения не являются результатом работы VTK по рассечению фигуры, а являются отдельным, специально вычисленным множеством точек. Таким образом, для каждого отображения задаются четыре поверхности: внешняя (константа), внутренняя (расчет) и два азимутальных сечения (расчет).
Достоверность прогноза остаточной толщины футеровки стенок горна ДП определяется сравнением результатов расчета в модели с результатами проведенных мероприятий УЗК.
Выводы
Применение разработанной математической модели позволит оптимизировать процесс доменной плавки, обеспечивая оперативный контроль толщины футеровки посредством визуализации горна и лещади. Это, в свою очередь, откроет путь к существенному сокращению издержек благодаря своевременному принятию решений о технологических параметрах процесса.
Список литературы
1. Чайка А.Л., Лебедь В.В., Сохацкий А.А., Цюпа К.С., Корнилов Б.В., Шостак В.Ю., Панчоха Г.В., Москалина А.А., Гоман С.В., Фоменко А.П. Опыт и перспективы комплексного применения систем автоматизированного контроля разгара футеровки, тепловых потерь и теплоэнергетических параметров на доменных печах. Металлургическая и горнорудная промышленность. 2017;(3):2–9.
2. Пинчук Д.А., Панчоха Г.В., Канаев В.В., Можаренко Н.М. Современные методы контроля остаточной толщины футеровки металлоприемника доменной печи: Сборник научных трудов «Фундаментальные и прикладные проблемы черной металлургии». 2005;(11):247–253.
3. Филатов С.В., Курунов И.Ф., Гордон Я.М., Тихонов Д.Н., Грачев С.Н. Продление кампании доменной печи при ее интенсивной работе. Металлург. 2016;(9):17–22.
4. Тараканов А.К., Иващенко В.П., Еремин О.О., Сибир А.В., Лялюк В.П., Кассим Д.А. Контроль состояния футеровки металлоприемника доменной печи. Металлургическая и горнорудная промышленность. 2016;(2):32–38.
5. Муравьева И.Г., Тогобицкая Д.Н., Белошапка Е.А., Шумельчик Е.И., Семенов Ю.С. Разработка комплексного критерия оценки воздействия расплавов на футеровку металлоприемника доменной печи: Сборник научных трудов «Системные технологии». 2012;(2):79.
6. Jiao K.-x., Zhang J.-l., Liu Z.-j., Deng Y., Chen C.-l. Cooling phenomena in blast furnace hearth. Journal of Iron and Steel Research International. 2018;25:1010–1016. https://doi.org/10.1007/s42243-018-0160-x
7. Andreev K., Louwerse G., Peeters T., van der Stel J. Blast furnace campaign extension by fundamental understanding of hearth processes. Ironmaking & Steelmaking. 2017;44(2): 81–91. https://doi.org/10.1080/03019233.2016.1154716
8. Liu Z Recent progress on long service life design of Chinese blast furnace hearth. ISIJ International. 2012;52(101): 1713–1723. https://doi.org/10.2355/isijinternational.52.1713
9. Li Y., Chen L., Wang L., Ma J. Monitoring the safety status of a blast furnace hearth using cooling stave heat flux. AIP Advances. 2020;10(2):025308. https://doi.org/10.1063/1.5137827
10. Dmitriev A.N., Chesnokov Yu.A., Chen K., Ivanov O.Yu., Zolotykh M.O. Monitoring system of firebrick lining erosion of blast furnace hearth. IFAC Proceedings Volumes. 2013;46(16):294–301. https://doi.org/10.3182/20130825-4-US-2038.00027
11. Дмитриев А.Н., Золотых М.О., Витькина Г.Ю. Мониторинг состояния огнеупорной футеровки горна доменной печи на основе цифровых технологий. Екатеринбург: АМБ;2022:154.
12. Пат. 2299910 RU. Способ контроля состояния футеровки горна доменной печи. Кошелев А.Е., Криволапова Л.И., Кравцова О.А.; заявлено 07.07.2005; опубликовано 27.05.2007.
13. Torrkulla J., Saxén H. Model of the state of the blast furnace hearth. ISIJ International. 2000;40(5):438–447. https://doi.org/10.2355/isijinternational.40.438
14. Duarte R.M., Ruiz-Bustinza I., Carrascal D., Verdeja L.F., Mochón J., Cores A. Monitoring and control of hearth refractory wear to improve blast furnace operation. Ironmaking & Steelmaking. 2013;40(5):350–359. https://doi.org/10.1179/1743281212Y.0000000045
15. Swartling M., Sundelin B., Tilliander A., Jönsson P.G. Heat transfer modelling of a blast furnace hearth. Steel Research International. 2010;81(3):186–196. https://doi.org/10.1002/srin.200900145
16. Swartling M. A study of the heat flow in the blast furnace hearth lining: Doctoral dissertation. 2010:51.
17. Li Y., Chen L., Ma J. Numerical study on the relationship between the localized depression erosion of a commercial blast furnace hearth lining and the heat flux of cooling staves. IEEE Access. 2019;(7):60984–60994. https://doi.org/10.1109/ACCESS.2019.2915915
18. Swartling M., Sundelin B., Tilliander A., Jönsson P. Experimentally determined temperatures in blast furnace hearth. Ironmaking & Steelmaking. 2010;37(1):21–26. https://doi.org/10.1179/030192309X12506804200627
19. Zhao H., Cheng S. Optimization for the structure of BF hearth bottom and the arrangement of thermal couples. Journal of University of Science and Technology Beijing, Mineral, Metallurgy, Material. 2006;13(6):497–503. https://doi.org/10.1016/S1005-8850(06)60101-1
20. Zhang C., Hou B., Shao L., Zou Z., Saxén H. Estimation of the blast furnace hearth state using an inverse-problem-based wear model. Metals. 2022;12(8):1302. https://doi.org/10.3390/met12081302
21. Дмитриев А.Н., Золотых М.О., Чэнь К., Витькина Г.Ю. Сравнительный технологический анализ систем контроля разгара огнеупорной футеровки горна доменной печи. Черная металлургия. Бюллетень научно-технической и экономической информации. 2018;(8):82–91.
22. Мороз В.Ф., Тогобицкая Д.Н., Можаренко Н.М., Нестеров А.С., Белькова А.И., Степаненко Д.А. Влияние состава и свойств материалов гарнисажа на его образование и стойкость: Сборник научных трудов «Фундаментальные и прикладные проблемы черной металлургии». 2010;22:85–95.
Об авторах
А. Н. ДмитриевРоссия
Андрей Николаевич Дмитриев, д.т.н., главный научный сотрудник лаборатории пирометаллургии восстановительных процессов
Россия, 620016, Екатеринбург, ул. Амундсена, 101
Д. А. Витькин
Россия
Дмитрий Александрович Витькин, инженер-конструктор
Россия, 620078, Екатеринбург, ул. Мира, 33)
М. О. Золотых
Россия
Максим Олегович Золотых, к.т.н., ведущий инженер лаборатории пирометаллургии восстановительных процессов
Россия, 620016, Екатеринбург, ул. Амундсена, 101
Г. Ю. Витькина
Россия
Галина Юрьевна Витькина, к.т.н., ведущий научный сотрудник, заведующий лабораторией пирометаллургии восстановительных процессов
Россия, 620016, Екатеринбург, ул. Амундсена, 101
Рецензия
Для цитирования:
Дмитриев А.Н., Витькин Д.А., Золотых М.О., Витькина Г.Ю. Математическая модель состояния горна доменной печи на основе показаний термопар, находящихся в поясах холодильников. Известия высших учебных заведений. Черная Металлургия. 2025;68(3):316-323. https://doi.org/10.17073/0368-0797-2025-3-316-323
For citation:
Dmitriev A.N., Vit’kin D.A., Zolotykh M.O., Vit’kina G.Yu. Mathematical model of blast furnace hearth condition based on data from thermocouples in refrigerator belts. Izvestiya. Ferrous Metallurgy. 2025;68(3):316-323. https://doi.org/10.17073/0368-0797-2025-3-316-323
JATS XML