Перейти к:
Оптимизационное моделирование трещиностойкости керамической оболочковой формы при охлаждении в ней стальной отливки
https://doi.org/10.17073/0368-0797-2025-3-297-304
Аннотация
В статье приводится подробный анализ отечественных и зарубежных работ по исследованию напряженно-деформированного состояния в оболочковой форме (ОФ) при получении металлических отливок. Экспериментальные и теоретические исследования являются важными для совершенствования технологии получения качественных литейных изделий. В настоящей работе сформулирована и решена задача по снижению уровня напряженно-деформированного состояния в литейной керамической оболочковой форме путем уменьшения образующихся растягивающих напряжений на ее наружной поверхности за счет выполнения температурных швов (выточек). В качестве определяющего трещиностойкость параметра принимается нормальное растягивающее напряжение σ22 , возникающее на наружной поверхности ОФ в начальный момент заливки металла и охлаждения в ней стальной отливки. Рассматриваемая задача является осесимметричной. Оболочковая форма имеет сферические и цилиндрические участки. Авторы сформулировали целевую функцию, привели численную схему и разработанный алгоритм решения задачи на основе уравнений линейной теории упругости, уравнений теплопроводности и апробированных численных методов. Результатом решения модельной задачи являются найденное оптимальное геометрическое местоположение температурных швов в форме кольцевых выточек и их количество. Поля напряжений приводятся в виде эпюр по сечениям рассматриваемой области при наличии и отсутствии температурных швов. Для убедительности предлагаемого способа (выполнения температурных швов) в тестовом примере рассматривается наиболее жесткий вариант, в котором не используются установленные ранее в предыдущих работах факторы, влияющие на уменьшение растягивающих напряжений на внешней поверхности ОФ. Полученные результаты характеризуют стойкость керамической литейной формы к образованию трещин и демонстрируют целесообразность и эффективность предложенной технологии изготовления литейной керамической оболочковой формы.
Ключевые слова
Для цитирования:
Евстигнеев А.И., Чернышова Д.В., Одиноков В.И., Дмитриев Э.А., Евстигнеева А.А. Оптимизационное моделирование трещиностойкости керамической оболочковой формы при охлаждении в ней стальной отливки. Известия высших учебных заведений. Черная Металлургия. 2025;68(3):297-304. https://doi.org/10.17073/0368-0797-2025-3-297-304
For citation:
Evstigneev A.I., Chernyshova D.V., Odinokov V.I., Dmitriev E.A., Evstigneeva A.A. Optimization modeling of crack resistance of ceramic shell mold during cooling of steel casting in it. Izvestiya. Ferrous Metallurgy. 2025;68(3):297-304. (In Russ.) https://doi.org/10.17073/0368-0797-2025-3-297-304
Введение
Высокий уровень напряженно-деформированного состояния (НДС) является основной причиной образования макро- и микротрещин в оболочковых формах (ОФ), а также их полного разрушения за счет температурного воздействия при заливке жидким металлом на начальной стадии охлаждения затвердевающей отливки.
Изучению НДС ОФ посвящены работы как отечественных, так и зарубежных исследователей. Рассмотрены влияние формы и геометрии ОФ [1; 2], толщины стенки формы [3; 4], материала формы [5; 6], геометрии отливки [7 ‒ 9].
Настоящая работа является продолжением целой серии работ, в которых рассматривались различные факторы, влияющие на стойкость литейной ОФ при кристаллизации в ней стальной отливки: физические свойства исходных материалов и самой ОФ; ее морфологическая структура; факторы внешнего воздействия со стороны опорного наполнителя (ОН). Значительное влияние на трещиностойкость оказывает конфигурация ОФ. Было показано, что наиболее опасными являются нормальные растягивающие напряжения, которые возникают на наружной поверхности оболочковой формы в начальный момент заливки металла и охлаждения в ней стальной отливки.
В работах [10 ‒ 12] представлено математическое моделирование рассматриваемых процессов с использованием численных методов. В работе [13] приводится общая постановка задачи по построению математической модели расчета НДС и температуры в ОФ при затвердевании в ней сферической отливки, а в работе [14] ‒ результаты решения поставленной задачи по предложенной математической модели, численной схеме и алгоритму с использованием численного метода [15] и авторской программы [16].
Поиски новых решений по снижению критического уровня НДС в ОФ базируются на новейших конструкторско-технологических разработках, результатах изучения их структурного морфологического строения. Так, в работах [17; 18] рассчитаны температурные напряжения в сферической керамической оболочковой форме в процессе заливки и затвердевания металла. Одной из последних разработок является литейная керамическая ОФ, предложенная в Комсомольском-на-Амуре государственном университете, на конструкцию которой получен патент1.
При заливке жидким металлом на наружной поверхности ОФ с цилиндрическими участками возникают значительные растягивающие напряжения, которые могут привести к образованию микро- и макротрещин, что, в свою очередь, может способствовать разрушению оболочковой формы. Наличие в этих зонах кольцевых температурных швов обеспечивает снижение растягивающих напряжений до рабочего уровня.
Целью настоящей работы является установление особенностей влияния температурных швов в виде кольцевых выточек на НДС ОФ при их заливке металлом и охлаждении формирующейся стальной отливки. Показана эффективность уменьшения растягивающих напряжений по наружной поверхности ОФ за счет выполнения на ней температурных швов.
Математическая постановка задачи
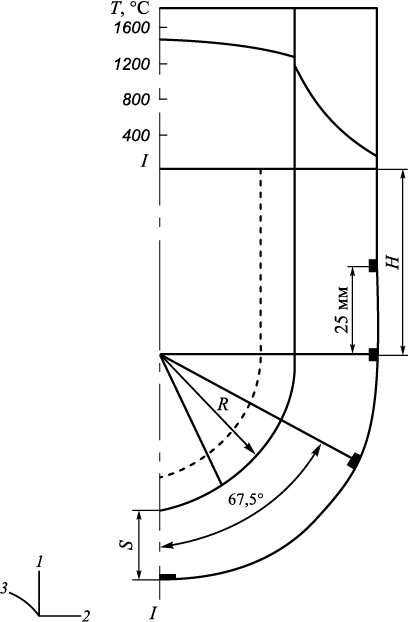
Рассматривается осесимметричное тело вращения, содержащее сферический и цилиндрический участки. На рис. 1 показана схема литейной формы (ЛФ) с учетом осевой симметрии (I ‒ жидкий металл; II ‒ затвердевающая корочка металла; III ‒ оболочковая форма; IV ‒ опорный наполнитель; ai ‒ круговые выточки на поверхности; S3 – поверхность соприкосновения формы III с опорным наполнителем IV).
Рис. 1. Расчетная схема системы с указанием поверхности |
Требуется найти минимальное количество и геометрическое расположение круговых выточек \({\left. {{a_i}} \right|_{{S_3}}}\), чтобы литейная форма III не разрушилась при охлаждении в ней стальной отливки.
Пусть А – конечное множество круговых выточек ai на поверхности S3 ; A = {ai , i = 1, ..., n}. Как известно, наиболее опасными напряжениями при заливке стали в ОФ являются нормальные растягивающие напряжения σ22 и в меньшей степени σ33 . При охлаждении стали в ОФ с цилиндрическими участками наиболее опасными являются растягивающие напряжения σ22 на поверхности S3 .
В процессе охлаждения отливки в ОФ наблюдаются следующие периоды: рост нормальных напряжений (по модулю) из-за большой неравномерности температуры в поперечном сечении ОФ; далее поле температур по сечению выравнивается и начинается уменьшение нормальных напряжений (по модулю). Таким образом, имеется максимальное время охлаждения (τ*), при котором наблюдается максимум величины σii .
Значение τ* определим из функции:
| F = max σ22 (τ, Q) | (1) |
при ограничении τ ≤ 60 с.
Для определения величины F запишем систему уравнений в декартовой системе координат для каждой из подобластей (рис. 1), используя уравнения линейной теории упругости:
‒ область I:
| \[{\sigma _{11}} = {\sigma _{22}} = {\sigma _{33}} = \sigma = {P_1};{\rm{ }}{P_1} = - \gamma h;{\rm{ }}\dot \theta = {a_1}\Delta \theta ;\] | (2) |
‒ области II, III:
| \[\left\{ \begin{array}{l}{{\rm{\sigma }}_{ij,j}} = 0,{\rm{ }}i{\rm{, }}j{\rm{ = 1}}{\rm{, 2}}{\rm{, 3; }}\\{{\rm{\sigma }}_{ij}} - {\rm{\sigma }}{{\rm{\delta }}_{ij}} = 2{G_p}{\rm{\varepsilon }}_{ij}^ * {\rm{; \varepsilon }}_{{\rm{ij}}}^ * = {{\rm{\varepsilon }}_{ij}} - \frac{1}{3}{\rm{\varepsilon }}{{\rm{\delta }}_{ij}}{\rm{; \varepsilon }} = {{\rm{\varepsilon }}_{ii}}{\rm{;}}\\{{\rm{\varepsilon }}_{ii}} = 3{k_p}{\rm{\sigma }} + 3{{\rm{\alpha }}_p}\left( {{\rm{\theta }} - {\rm{\theta }}_p^ * } \right){\rm{; }}{{\rm{\varepsilon }}_{{\rm{ij}}}} = 0,5\left( {{U_{i,j}} + {U_{j,i}}} \right){\rm{;}}\\{C_p}{\rm{\gamma }}\frac{{\partial {\rm{\theta }}}}{{\partial {\rm{\tau }}}} = {\rm{div}}({\rm{\lambda grad\theta }});\end{array} \right.\] | (3) |
где σij – компоненты тензора напряжений; σ – гидростатическое напряжение; εij – компоненты тензора упругих деформаций; h – текущая высота столба жидкого металла; \({k_p}(\theta ) = \frac{{1 - 2\mu }}{E}\) – коэффициент объемного сжатия; m ‒ коэффициент Пуассона; E – модуль Юнга; Gp(θ) – модуль сдвига в области p (p = II, III); αp – коэффициент линейного расширения; a1 – температуропроводность в области I; τ – время; θ – температура; Cp – удельная теплоемкость в области p; γ – удельный вес металла; \(\theta _p^*\) – начальная температура в области р; λ = λ(θ) – коэффициент теплопроводности; δij – символ Кронекера; используется суммирование по повторяющимся индексам.
В процессе охлаждения жидкого металла при условии θм ≤ θк (где θм и θк – температура металла и кристаллизации) определяется толщина затвердевшего слоя Δi из решения уравнения межфазового перехода [19]:
| \[{\Delta _n} = C\sqrt \tau ;{\rm{ }}C = \sqrt {\frac{{2\Delta {\theta _1}{\lambda _1}}}{{\rho L}}} ;\] | (4) |
здесь Δθ1 – перепад температур в твердой фазе вблизи фронта кристаллизации; λ1 – коэффициент теплопроводности в твердой фазе; L – скрытая теплота плавления; ρ – плотность твердой фазы; Δn – толщина корочки на n-ом временном шаге.
Начальные условия задачи:
– \({\left. \Delta \right|_{\tau = 0}} = 0\) – отсутствие твердой фазы металла;
– \({\left. {\theta _I^*} \right|_{\tau = 0}} = \theta _{\rm{м}}^*\) – температура разливаемого жидкого металла;
– \({\left. {\theta _{III}^*} \right|_{\tau = 0}} = {\theta ^*}\) – начальная температура формы.
Граничные условия задачи (рис. 1) в ортогональных координатах:
‒ для осесимметричной задачи
| \[\begin{array}{c}{U_3} = 0;{\rm{ }}{{\rm{\sigma }}_{31}} = {{\rm{\sigma }}_{32}} = 0;{\rm{ }}{{\rm{\varepsilon }}_{13}} = {{\rm{\varepsilon }}_{23}} = 0;{\rm{ }}\;\\\frac{{\partial {u_i}}}{{\partial {x_3}}} = 0;{\rm{ }}\frac{{\partial {{\rm{\sigma }}_{3i}}}}{{\partial {x_3}}} = 0;{\rm{ }}i = 1,{\rm{ }}2,{\rm{ }}3;\end{array}\] | (5) |
‒ на оси симметрии
\[{U_2} = 0;{\rm{ }}{{\rm{\sigma }}_{21}} = 0;{\rm{ }}{q_n} = 0;{\rm{ }}\theta = {\theta _{\rm{м}}};\]
‒ на поверхностях S1 , S3 , S4
| \[\begin{array}{c}{\left. {{\sigma _{11}}} \right|_{{S_1}}} = - P;{\left. {{\rm{ }}{\sigma _{12}}} \right|_{{S_1}}} = 0;{\rm{ }}{\left. {{U_1}} \right|_{{{S'}_3}}} = 0;{\rm{ }}{\left. {{\sigma _{21}}} \right|_{{S_4}}} = 0;\\{\left. {{\sigma _{22}}} \right|_{{S_4}}} = 0;{\left. {{\rm{ }}{\sigma _{11}}} \right|_{{{S''}_3}}} = 0;\\{\left. {{\sigma _{12}}} \right|_{{{S'}_3}}} = - \psi \frac{{{U_{{\rm{ск}}}}}}{{{U^*}}}{\tau _s}\cos ({n_1}{x_1});{\rm{ }}{\left. \theta \right|_{{S_3}}} = {\theta ^*};{\rm{ }}{\left. \theta \right|_{{S_2}}} = {\theta _{\rm{м}}},\end{array}\] | (6) |
где Uск – скольжение материала формы относительно ОН (песка); U * – нормирующее перемещение; ψ – параметр, характеризующий условия трения между формой и опорным наполнителем; τs – условный предел текучести при сдвиге; qn – тепловой поток; \({S'_3}\) ‒ контактная поверхность; \({S''_3}\) ‒ свободная поверхность.
Решение систем уравнений (2), (3) при наличии начальных и граничных условий (6) осуществляется численным методом, описанным в работе [15].
При решении температурной задачи использовали граничные условия первого рода. Для определения θм(τ) и θ*(τ) воспользуемся данными работы [20], по которым получим следующие формулы:
| \[\begin{array}{c}{\theta _{\rm{м}}} = \theta _{\rm{м}}^* - \frac{\tau }{{{\tau _1}}}{\theta _1};\\0 \le \tau \le 60{\rm{ c}};\\{\theta ^*} = {\theta _{\rm{o}}}\left( {1 + \sqrt {\frac{\tau }{{{\tau _2}}}} } \right),\end{array}\] | (7) |
где τ – время охлаждения, с; \(\theta _{\rm{м}}^*\) = 1550 °C; θ1 = 100 °C; τ1 = 60 с; τ2 = 1 с.
Время τ не превышает 60 с, так как при τ ≥ 60 с напряжения в ОФ не представляют опасности разрушения.
Алгоритм решения задачи F
1. Время охлаждения τ разбивается на конечное число шагов: \(\tau = \sum {\Delta {\tau _n}} \); здесь n ‒ номер временного шага; задаются геометрические размеры.
2. Исследуемая область разбивается системой ортогональных поверхностей на конечное число элементов.
3. В соответствии с работой [15] вычисляются длины дуг элементов (i, k = 1, 2, 3; i ≠ k; j = 1, 2).
4. Задаются начальные и граничные условия по элементам, образующим рассматриваемую область, и константы физико-механических свойств материалов.
5. Определяется поле температур на временном шаге Δτn численным решением уравнения теплопроводности с использованием итерационной формулы, полученной в работе [15], при наличии начальных и граничных условий на рассматриваемом временном шаге.
6. Если температура в области I (рис. 1) у поверхности S2\({\left. \theta \right|_{{S_2}}} \le {\theta _{\rm{к}}}\), то вычисляется толщина закристаллизовавшейся корочки Δn по формуле (4).
7. Решается система уравнений (3) с учетом начальных и граничных условий, разностных аналогов и разработанной методики, описанной в работе [15], с использованием комплекса программ [16]. Определяются поля напряжений σij и перемещений Ui (i, j = 1, 2, 3).
8. На поверхности S3 проводится оценка прилегания формы к ОН по каждому элементу: если \({\left. {{\sigma _{11}}} \right|_{{S_3}}} > 0 \Rightarrow {\sigma _{11}} = 0,{\rm{ }}{\sigma _{12}} = 0,\) следует переназначение граничных условий и выполняется операция 7. Уточняются физические величины, зависящие от температуры.
9. По области Q анализируются напряжения σ22 , выбирается наибольшее и запоминается в соответствии с данным временным шагом. Формируется матрица \(\left\| {\sigma _{22}^*} \right\|\).
10. Проводится шаг по времени. По формулам (7) уточняются граничные условия решения температурной задачи. Если на n-ой итерации max | σ22 |n < max | σ22 |n – 1 , тогда выполняется операция 11, если max | σ22 |n > max | σ22 |n – 1 , то выполняется операция 5.
11. Из матрицы \(\left\| {\sigma _{22}^*} \right\|\) находим max σ22 и соответствующее время τ = τ*.
Результаты решения задачи
Геометрические параметры: S = 5 мм, R = 20 мм.
Временные интервалы Δτn : 0,01; 0,02; 0,03; 0,04; 0,05; 0,1; 0,2; 0,3; 0,4; 0,5; 2,0; 5,0; 5,0; 5,0; 3,0; 3,0; 5,0; 5,0; 5,0; 5,0 с;
Разбиение области: N1×N2 = 9×13;
Приняты следующие физические параметры разливаемой стали при θ > 1000 °C (\(\theta _{\rm{м}}^*\) = 1500 °C) [20]:
G = 1000 кг/мм2; α = 12·10–6 °С‒1; | (8) |
где L = 270·103 Дж/кг (скрытая теплота плавления); C = 444 Дж/(кг·°C); γ = 7,80·10–6 кг/мм3; θк = 1450 °C.
Физические свойства керамической формы:
Gф = 2960 кг/мм2; α = 0,51·10–6 °С‒1; | (9) |
Принято усредненное значение модуля сдвига формы Gф , не зависящее от температуры.
Расчет по приведенному выше алгоритму с использованием комплекса программ работы [16] показал следующее:
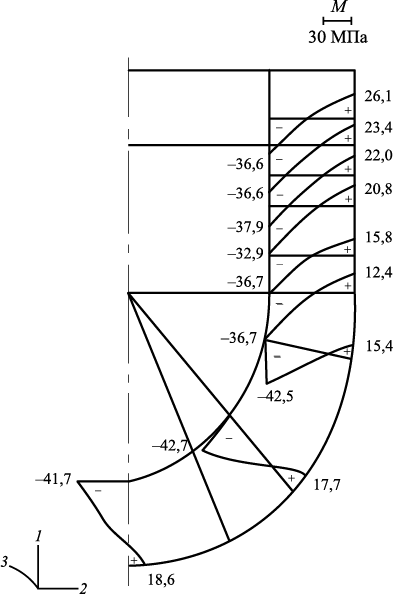
F = 26,1 МПа; τ* = 21,65 с. | (10) |
Результат решения приведен на рис. 2 в виде эпюр по сечению рассматриваемой оболочки. Напряжения σ22 весьма значимы. На облицовочном слое σ22 отрицательны и достигают величины ‒42,7 МПа. На наружном слое (контакте с опорным наполнителем) напряжения σ22 положительны и возрастают к верхней части формы. Напряжения σ22 при заливке стали в керамическую форму с физическими характеристиками (8), (9) довольно высоки.
Рис. 2. Эпюры нормальных напряжений σ22 по сечению литейной ОФ |
Зная значения τ* (10), перейдем к решению задачи по определению множества {A}. При рассмотрении процесса охлаждения стали в керамической форме, имеющей температурные швы (круговые выточки) на поверхности S3 , имеет место ограничение:
σ22 < 20 МПа. | (11) |
В отличие от предыдущей задачи сечение Q представляет многосвязную область. Начальные и граничные условия во многом совпадают с предыдущей задачей. Граничные условия (6) дополняются (рис. 1):
\[{\left. {({\sigma _{22}} = {\sigma _{21}})} \right|_{{S_i}}} = 0;{\rm{ }}i = 7,{\rm{ }}8;{\rm{ }}{\left. {({\sigma _{11}} = {\sigma _{12}})} \right|_{{S_i}}} = 0;{\rm{ }}i = 5,{\rm{ }}6.\] | (12) |
Выполняется также соотношение (7).
Алгоритм решения задачи
1. Задаются геометрические размеры области, конечное время охлаждения τ*, геометрические размеры выточек (выточки). Время охлаждения τ* разбивается на конечное число шагов: τ* = \(\tau = \sum {\Delta {\tau _n}} \); здесь n ‒ номер временного шага.
2. Исследуемая область разбивается системой ортогональных поверхностей на конечное число элементов.
3. Вычисляются длины дуг элементов \(S_{ij}^k\) (i, k = 1, 2, 3; i ≠ k; j = 1, 2) в соответствии с работой [15].
4. Задаются начальные и граничные условия по элементам, образующим рассматриваемую область ((5), (6), (12)), и константы физико-механических свойств материалов.
5. Определяется поле температур на временном шаге Δτn численным решением уравнения теплопроводности с использованием итерационной формулы, полученной в работе [15], при наличии начальных и граничных условий на рассматриваемом временном шаге. Наличие выточек при решении температурной задачи не учитывалось.
6. Если в области I у поверхности S2 выполняется условие \({{{\left. \theta \right|}_{{S_2}}} \le {\theta _{\rm{к}}}}\), то вычисляется толщина закристаллизовавшейся корочки Δn по формуле (4).
7. Решается система уравнений (2), (3) с учетом начальных и граничных условий (5), (6), (12), разностных аналогов и разработанной методики, описанной в работе [15], с использованием программы [16]. Определяются поля напряжений σij и перемещений Ui (i, j = 1, 2).
8. На поверхности S3 проводится оценка прилегания формы к ОН по каждому элементу: если \({\left. {{\sigma _{11}}} \right|_{{S_3}}} > 0 \Rightarrow {\sigma _{11}} = 0,{\rm{ }}{\sigma _{12}} = 0,\) то осуществляется переназначение граничных условий и выполняется операция 7.
9. Проводится шаг по времени. По формулам (7) уточняются граничные условия решения температурной задачи: если \(\tau = \sum {\Delta {\tau _n}} \) > τ*, то выполняется операция 5; если \(\tau = \sum {\Delta {\tau _n}} \) = τ* ‒ выполняется операция 10.
10. По области Q анализируются напряжения σ22 и выбираются наибольшие.
11. Находятся первые по координате x2 напряжения \({\left. {{\sigma _{22}}} \right|_{{S_3}}}\) , превосходящие ограничения (11), и в этом сечении по координате x2 устанавливается выточка ai . В случае, если после установки и последующего просчета 5 получим, что \({\sigma _{{{22}_n}}} > {\sigma _{{{22}_{n - 1}}}}\), то выточка (ai )n – 1 остается на месте по поверхности S3 и вводится следующая выточка ai на месте, где \({\sigma _{{{22}_n}}}\) больше ограничений, и следует операция 5.
12. Процесс расчета заканчивается, когда по области Q будут выполнены ограничения (11).
Результаты решения задачи
Геометрические размеры, временные интервалы, разбиение области такие же, как и в предыдущей задаче. Физические свойства разливаемой стали (8), физические свойства керамики (9), размеры выточек: ai = (Δx1 , Δx2 ), Δx1 = 1 мм, Δx2 = 3 мм.
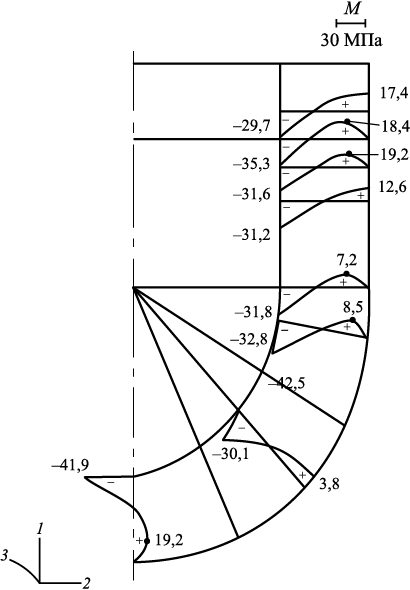
Расчет по приведенному выше алгоритму показал следующие значения: A {1, 2, 3, 4}; max σ22 = 19,2 МПа, геометрическое местоположение выточек и температуры в сечении показаны на рис. 3. Полученные результаты по напряжениям σ22 приведены на рис. 4.
Рис. 3. Схема расположения выточек в сечении ОФ
Рис. 4. Эпюры нормальных напряжений σ22 по сечению ОФ |
Видим, что внутренняя область ОФ, контактирующая с металлом, находится в состоянии сжатия, а внешний (наружный) и прилегающие слои находятся под воздействием небольших растягивающих напряжений. Наибольшие по модулю сжимающие напряжения имеют место в облицовочном слое донной сферической части ОФ, а растягивающие ‒ в прилегающих к наружному слоях. Все максимальные значения напряжений отвечают ограничению (11), хотя и очень близки в некоторых сечениях к граничным значениям.
Новизной настоящей работы являются как постановка задачи, так и значения напряжений в ОФ, а также алгоритм решения. Сформулирована и решена задача математического программирования по влиянию на НДС ОФ выточек и мест их нанесения при затвердевании стальной отливки на НДС ОФ. Аналогичных задач в такой постановке не решалось, полученные результаты имеют важное практическое значение.
Выводы
Поставлена осесимметричная задача математического программирования по оптимизации процесса охлаждения стальной отливки в керамической форме, поверхность которой имеет как цилиндрические, так и сферические участки, на которых выполнены температурные швы (кольцевые выточки). На основе уравнений линейной теории упругости и численных методов разработаны алгоритм и программа по определению оптимального влияния выточек на НДС ОФ при затвердевании стальной отливки. На примере решения частной задачи показана эффективность выполнения кольцевых температурных швов на наружной поверхности ОФ, соприкасающейся с ОН, для снижения образующихся растягивающих напряжений на внешней поверхности ОФ.
Список литературы
1. Kanyo J.E., Schafföner S., Uwanyuze R.Sh., Leary K.S. An overview of ceramic molds for investment casting of nickel superalloys. Journal of the European Ceramic Society. 2020;40(15):4955–4973. https://doi.org/10.1016/j.jeurceramsoc.2020.07.013
2. Rafique M.M.A., Iqbal J. Modeling and simulation of heat transfer phenomena during investment casting. International Journal of Heat and Mass Transfer. 2009;52(7-8):2132–2139. http://doi.org/10.1016/j.ijheatmasstransfer.2008.11.007
3. Singh R. Mathematical modeling for surface hardness in investment casting applications. Journal of Mechanical Science and Technology. 2012;26:3625–3629. http://dx.doi.org/10.1007/s12206-012-0854-0
4. Jafari H., Idris M.H., Ourdjini A. Effect of thickness and permeability of ceramic shell mould on in situ melted AZ91D investment casting. Applied Mechanics and Materials. 2014;465-466:1087–1092. http://dx.doi.org/10.4028/www.scientific.net/AMM.465-466.1087
5. Bansode S.N., Phalle V.M., Mantha S.S. Taguchi approach for optimization of parameters that reduce dimensional variation in investment casting. Archives of Foundry Engineering. 2019;19(1):5–12. https://dx.doi.org/10.24425/afe.2018.125183
6. Pattnaik S., Karunakar D.B., Jha P.K. Developments in investment casting process ‒ A review. Journal of Materials Processing Technology. 2012;212(11):2332–2348. https://doi.org/10.1016/j.jmatprotec.2012.06.003
7. Zhang J., Li K.W., Ye H.W., Zhang D.Q., Wu P.W. Numerical simulation of solidification process for impeller investment casting. Applied Mechanics and Materials. 2011;80-81:961–964. https://doi.org/10.4028/www.scientific.net/AMM.80-81.961
8. Dong Y.W., Li X.L., Zhao Q., Jun Y., Dao M. Modeling of shrinkage during investment casting of thin-walled hollow turbine blades. Journal of Materials Processing Technology. 2017;244:190–203. https://doi.org/10.1016/j.jmatprotec.2017.01.005
9. Rakoczy Ł., Cygan R. Analysis of temperature distribution in shell mould during thinwall superalloy casting and its effect on the resultant microstructure. Archives of Civil and Mechanical Engineering. 2018;18(4):1441–1450. https://doi.org/10.1016/j.acme.2018.05.008
10. Sabau A.S. Numerical simulation of the investment casting process. Transactions of American Foundry Society. 2005;113:407–417.
11. Zheng K., Lin Y., Chen W., Liu L. Numerical simulation and optimization of casting process of copper alloy water-meter shell. Advances in Mechanical Engineering. 2020;12(5): 1–12. http://dx.doi.org/10.1177/1687814020923450
12. Manzari M.T., Gethin D.T., Lewis R.W. Optimisation of heat transfer between casting and mould. International Journal of Cast Metals Research. 2000;13(4):199–206. https://doi.org/10.1080/13640461.2000.11819402
13. Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Намоконов А.Н., Евстигнеева А.А., Чернышова Д.В. Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 1. Известия вузов. Черная металлургия. 2024;67(2):211‒218. https://doi.org/10.17073/0368-0797-2024-2-211-218
14. Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Намоконов А.Н., Евстигнеева А.А., Чернышова Д.В. Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 2. Известия вузов. Черная металлургия. 2024;67(4):463‒470. https://doi.org/10.17073/0368-0797-2024-4-463-470
15. Математическое моделирование сложных технологических процессов / В.И. Одиноков, Б.Г. Каплунов, А.В. Песков, А.В. Баков. Москва: Наука; 2008:178.
16. Одиноков В.И., Прокудин А.Н., Сергеева А.М., Севастьянов Г.М. Свидетельство о государственной регистрации программы для ЭВМ № 2012111389. ОДИССЕЙ. Зарегистрировано в Реестре программ для ЭВМ 13.12.2012.
17. Ткачева А.В., Евстигнеева А.А. Об оценке влияния степени охвата опорным наполнителем сферической керамической оболочки и предварительной прокалки на уровень напряжений в материале формы при заливке и затвердевании в ней отливки. Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. 2024;(2(60)):24–34. https://doi.org/10.37972/chgpu.2024.60.2.002
18. Ткачева А.В., Евстигнеева А.А. О напряжениях в сферической керамической форме. В кн.: Вычислительные технологии и прикладная математика. Материалы III научн. конференции с международ. участием, Комсомольск-на-Амуре, 7 – 11 октября 2024; отв. ред. Э.А. Дмитриев. Комсомольск-на-Амуре: ФГБОУ ВО «КнАГУ»; 2024;351–355.
19. Евстигнеев А.И., Дмитриев Э.А., Чернышова Д.В., Одиноков В.И., Евстигнеева А.А., Иванкова Е.П. Моделирование внешнего силового воздействия на стойкость оболочковой формы при заливке в нее стали. Математическое моделирование. 2022;34(5):61–72. https://doi.org/10.20948/mm-2022-05-04
20. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И., Свиридов А.В. Математическое моделирование процессов получения отливок в керамические оболочковые формы. Москва: Инновационное машиностроение; 2020:224.
Об авторах
А. И. ЕвстигнеевРоссия
Алексей Иванович Евстигнеев, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Д. В. Чернышова
Россия
Дарья Витальевна Чернышова, аспирант кафедры «Авиастроение»
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
В. И. Одиноков
Россия
Валерий Иванович Одиноков, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Э. А. Дмитриев
Россия
Эдуард Анатольевич Дмитриев, д.т.н., доцент, ректор
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
А. А. Евстигнеева
Россия
Анна Алексеевна Евстигнеева, магистрант кафедры «Прикладная математика»
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Рецензия
Для цитирования:
Евстигнеев А.И., Чернышова Д.В., Одиноков В.И., Дмитриев Э.А., Евстигнеева А.А. Оптимизационное моделирование трещиностойкости керамической оболочковой формы при охлаждении в ней стальной отливки. Известия высших учебных заведений. Черная Металлургия. 2025;68(3):297-304. https://doi.org/10.17073/0368-0797-2025-3-297-304
For citation:
Evstigneev A.I., Chernyshova D.V., Odinokov V.I., Dmitriev E.A., Evstigneeva A.A. Optimization modeling of crack resistance of ceramic shell mold during cooling of steel casting in it. Izvestiya. Ferrous Metallurgy. 2025;68(3):297-304. (In Russ.) https://doi.org/10.17073/0368-0797-2025-3-297-304