Инициация плавления на границах зерен наклона в аустените в зависимости от угла разориентации

Введение

В последние десятилетия большое внимание уделяется нанокристаллическим материалам, к которым относят поликристаллы со средним размером зерна менее 100 нм. Эти материалы обладают необычными физико-механическими свойствами, что связано, главным образом, с большой, по сравнению с обычным крупнозернистым состоянием, объемной долей границ зерен, тройных стыков и других дефектов [1 ‒ 3]. Сверхмалые размеры зерен получают разными способами, которые включают, как правило, интенсивную пластическую деформацию. Иногда такие материалы получают путем спекания нанопорошков, конденсации из газовой фазы и т. д. Однако общими свойствами нанокристаллических материалов являются высокая степень неравновесности структуры и большие значения избыточной (или запасенной) энергии [1 ‒ 3]. Избыточная энергия, то есть отличие свободной энергии материала от энергии идеального кристалла при той же температуре (или, другими словами, энергия, которая может потенциально выделиться при трансформации структуры, например, при рекристаллизации), в нанокристаллических материалах обусловлена наличием высокой плотности дефектов: границ зерен, тройных стыков, дислокаций, дисклинаций и др. При этом набор дефектов и их тип в значительной степени зависят от метода получения нанокристаллической структуры и последующей обработки [1 ‒ 4].

Уникальные свойства наноматериалов во многом обусловлены высокой объемной долей поверхности и других границ раздела (межфазных, межзеренных). Одним из таких свойств, важных с точки зрения эксплуатации и технологии изготовления наноматериалов, является зависимость температуры плавления от эффективного размера: размера зерна, толщины пленки, диаметра наночастицы. Наиболее хорошо изучена зависимость температуры плавления наночастиц от их размера. В настоящее время известно, что температура плавления круглых наночастиц обратно пропорциональна их диаметру, что было продемонстрировано как экспериментально [5 ‒ 9], так и с помощью молекулярно-динамического (МД) моделирования [10 ‒ 14], а также объяснено в теоретических работах [15 ‒ 20].

Что касается материалов с нанокристаллической структурой, то в работах [21 ‒ 25] с помощью МД моделирования было показано, что плавление в них не является гомогенным процессом, оно начинается, как правило, со свободных поверхностей и границ зерен. Уменьшение среднего размера зерна приводит к уменьшению температуры плавления нанокристаллических серебра [22; 23] и алюминия [24; 25]. В работах [14; 26] также наблюдается уменьшение температуры плавления наночастиц никеля с нанокристаллической структурой по сравнению с монокристаллическими частицами.

Рассматриваемое явление снижения температуры плавления в зависимости от среднего размера зерна в нанокристаллическом материале по сравнению с монокристаллическими наночастицами сложнее и менее изучено, поскольку обуславливается наличием дефектов не одного типа, как, например, поверхности в случае частиц, а широкого спектра границ зерен разных типов с разной энергией и других дефектов. В настоящем исследовании внимание сконцентрировано на влиянии угла разориентации и, соответственно, энергии границ зерен наклона на температуру плавления и характер инициации плавления на границе. Рассматриваются границы наклона с осями разориентации \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) и \(\left\langle {111} \right\rangle\). В качестве объекта исследования выбран аустенит в связи с его широким практическим приложением.

Описание модели

Для описания межатомных взаимодействий в молекулярно-динамической модели использовался EAM потенциал [27], где он был получен на основе сопоставления с экспериментальными данными и ab initio расчетами различных свойств аустенита. Данный потенциал хорошо воспроизводит широкий спектр механических и структурно-энергетических свойств, он прошел успешную апробацию при моделировании различных процессов, включая процессы плавления [27 ‒ 29].

Расчетные ячейки имели форму параллелепипеда с размерами примерно 9,9×10,8×13,5 нм и содержали около 118 000 атомов (рис. 1). Граница зерен наклона создавалась в середине расчетной ячейки путем поворота двух кристаллов, двух половин ячейки, на угол разориентации θ вокруг оси \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) и \(\left\langle {111} \right\rangle\), которая совпадала с осью x на рис. 1. Для удержания границы зерен в центре расчетной ячейки в течение моделирования вдоль оси z (сверху и снизу расчетной ячейки на рис. 1) использовались фиксированные граничные условия: атомы, окрашенные в темно-серый цвет, оставались неподвижными в течение моделирования. Вдоль других осей использовались периодические граничные условия. Таким образом, в расчетной ячейке находилось две параллельных и аналогичных границы зерен. На рис. 1 с помощью визуализатора кристаллических фаз на основе метода CNA (Common Neighbor Analysis) [30] изображен пример расчетной ячейки, содержащей две границы, одну посередине и вторую на краю ячейки, с осью разориентации \(\left\langle {111} \right\rangle\) и углом разориентации 30° (далее ‒ \(\left\langle {111} \right\rangle\) 30°). После поворота кристаллов и процедуры удаления лишних атомов проводилась релаксация структуры в течение 20 пс при постоянной температуре 1000 К. При этом атомы смещались в положения, соответствующие минимуму энергии. Расчетная ячейка (рис. 1) получена после процедуры структурной релаксации.

Угол разориентации θ для границ \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) и \(\left\langle {111} \right\rangle\) варьировался от 0 до 30°. Таким образом, половина рассматриваемых границ (до 15°) относилась к малоугловым границам, то есть к границам с различимыми геометрически необходимыми зернограничными дислокациями, а другая половина (после 15°) ‒ к большеугловым границам. Как будет показано ниже, основной характеристикой, влияющей на процесс плавления, является энергия границы, которая для большеугловых границ, как правило, примерно одинакова, в связи с чем, например, большинство углов между границами в тройных стыках близки к 120° [31; 32]. Именно поэтому для всех рассматриваемых типов границ наклона в настоящей работе ограничились углом разориентации 30°.

В модели использовался NPT канонический ансамбль в сочетании с термостатом Нозе-Гувера. При плавлении происходит увеличение удельного объема вследствие разрушения кристаллической решетки, поэтому важным было поддержание давления постоянным и равным нулю. При изменении температуры тепловое расширение учитывалось, в том числе и для фиксированных областей на границах расчетной ячейки (темно-серые области на рис. 1). При использовании метода молекулярной динамики шаг интегрирования по времени составлял 2 фс.

Для определения температуры плавления использовался метод постепенного нагревания с построением зависимости средней потенциальной энергии атома от температуры, который часто используется в подобных задачах [10 ‒ 14; 26; 33 ‒ 35]. Температура повышалась линейно со скоростью 10¹² К/с путем соответствующего увеличения модулей скоростей атомов через определенный шаг по времени (5 пс в данном случае).

Результаты и их обсуждение

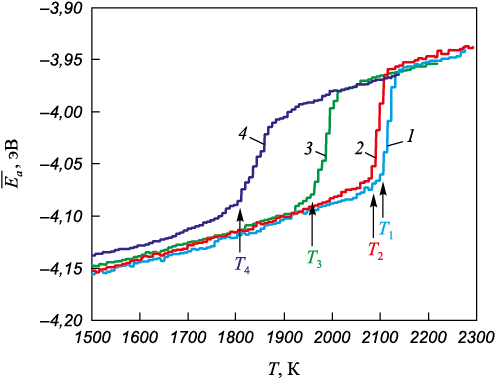
На рис. 2 показаны примеры зависимостей средней потенциальной энергии атома от температуры для расчетных ячеек с границами \(\left\langle {111} \right\rangle\) 6° (кривая 3) и \(\left\langle {111} \right\rangle\) 30° (кривая 4), а также для монокристаллического аустенита (кривые 1 и 2) при постепенном повышении температуры со скоростью 10¹² К/с в интервале от 1500 до 2300 К. С ростом температуры средняя энергия атома для одной и той же фазы растет почти линейно в связи с увеличением тепловых колебаний атомов и тепловым расширением. Резкое увеличение средней энергии атома на графиках соответствует фазовому переходу, то есть плавлению.

Структура в зафиксированных областях (рис. 1), как уже говорилось выше, оставалась кристаллической и после плавления, что, очевидно, оказывает влияние на процесс и температуру плавления всей расчетной ячейки. Однако мы вынуждены были использовать фиксированные границы ввиду важности удержания границ зерен с изначально заданными характеристиками в ячейке в течение всего моделирования. Для монокристаллического аустенита, то есть расчетной ячейки без каких-либо дефектов, было проведено дополнительное исследование влияния фиксированных границ на температуру плавления. На рис. 2 приведены зависимости средней энергии атома от температуры для монокристалла: при наличии фиксированных границ (кривая 1) и в случае периодических границ со всех сторон (кривая 2). Как можно видеть, плавление в случае наличия фиксированных границ, действительно, происходило при большей температуре по сравнению со случаем использования периодических условий со всех сторон. Тем не менее, отличие это было небольшим и слабо влияло на качественные результаты исследования.

В случае наличия границ зерен в расчетной ячейке плавление протекало гетерогенно, то есть инициировалось на границе, после чего фронт кристалл – жидкость двигался от границ в центр зерен с конечной скоростью, зависящей, как известно, от температуры. Величина скорости – порядка нескольких десятков метров в секунду [36; 37]. Статичной двухфазности, то есть одновременного пребывания части расчетной ячейки в жидком состоянии, а другой – в кристаллическом, в течение сравнительно продолжительного времени не наблюдалось: фронт всегда двигался в том или ином направлении. В связи с этим определяли температуру плавления по моменту начала фазового перехода (показан стрелками на рис. 2), который, в свою очередь, определяли по пересечению аппроксимационных прямых до и после начала плавления.

На рис. 2 хорошо видно, что плавление ячейки, содержащей большеугловую границу \(\left\langle {111} \right\rangle\) 30°, происходит при существенно более низкой температуре (1835 К), чем в случае малоугловой границы \(\left\langle {111} \right\rangle\) 6° (2013 К), что подтверждает влияние типа границы зерен на плавление. Энергия образования и, соответственно, степень нарушения кристаллической структуры в случае большеугловой границы выше.

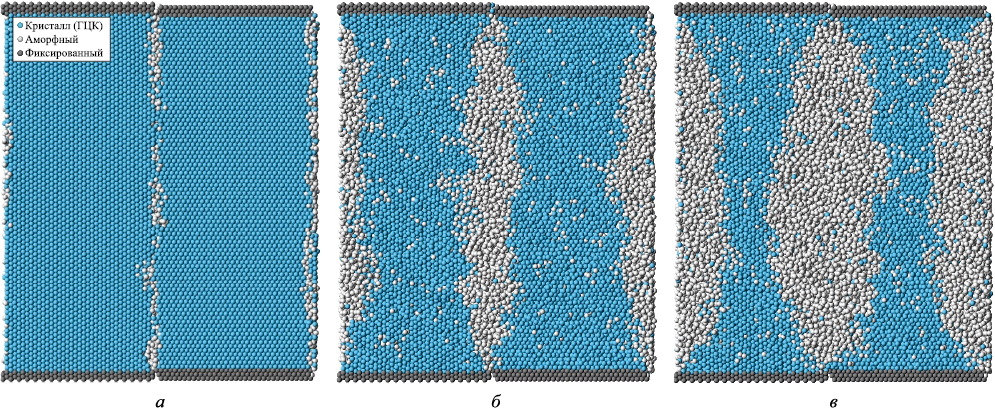
На рис. 3 с использованием визуализатора кристаллических фаз изображена расчетная ячейка в плоскости yz, содержащая две большеугловые границы \(\left\langle {111} \right\rangle\) 30° в разные моменты плавления. В основе визуализатора лежит метод CNA (Common Neighbor Analysis) [30], позволяющий определить принадлежность каждого атома к той или иной кристаллической структуре путем анализа расположения соседних атомов. В рассматриваемом случае атом считался принадлежащим к ГЦК решетке, если более 75 % его ближайших соседей располагались вблизи узлов идеального ГЦК кристалла (с учетом теплового расширения) в пределах заданной погрешности 25 % от радиуса первой координационной сферы. Атомы, не удовлетворяющие этим условиям, а также условиям принадлежности к ГПУ решетке, считались принадлежащими к аморфной структуре (на рис. 3 показаны белым цветом).

На рис. 3, а изображена начальная структура ячейки с двумя параллельными границами \(\left\langle {111} \right\rangle\) 30° после первичной структурной релаксации. В случае большеугловой границы дефект выглядит почти сплошным. Нарушение кристаллической структуры наблюдается вдоль всей границы. С ростом температуры плавление начиналось на границе почти равномерно вдоль нее (рис. 3, б), кроме областей вблизи зафиксированных границ (сверху и снизу расчетной ячейки), что является очевидным, поскольку в этих местах сказывается влияние зафиксированной кристаллической структуры на границах.

При дальнейшем увеличении температуры фронт кристалл – жидкость двигался от границ в остальной объем (рис. 3, в). Аморфной фазы (белые атомы) при этом становилось все больше. Можно заметить, что инициация плавления на границе происходила даже при меньшей температуре по сравнению со значением, найденным по графику (рис. 1) для всей расчетной ячейки. Дело в том, что на температуру плавления всей расчетной ячейки влияет плотность в ней границ зерен. В работах [22 ‒ 25] наблюдалась такая зависимость: по мере уменьшения среднего размера зерна в серебре или алюминии с нанокристаллической структурой температура плавления снижалась. В рассматриваемом случае это означает, что, например, при увеличении размера ячейки вдоль оси у следует ожидать снижения влияния границы зерен на температуру плавления.

Плавление с границ зерен начинается по причине сравнительно более легкого разрушения кристаллической структуры вблизи них из-за того, что атомы в дефектах находятся в менее глубоких потенциальных ямах по сравнению с чистым кристаллом и им легче их покинуть в результате тепловых колебаний. Атомы вблизи фронта кристалл – жидкость со стороны кристаллической фазы также находятся в сравнительно менее глубоких потенциальных ямах, чем в объеме кристалла, из-за более беспорядочного расположения атомов со стороны расплава. Кроме того, в расплаве более интенсивная самодиффузия и больше свободного объема по сравнению с кристаллом, что также является причиной более легкого разрушения кристалла вблизи фронта кристалл – жидкость, чем внутри объема кристалла, и причиной движения фронта.

На рис. 4 изображена расчетная ячейка, содержащая две малоугловые границы \(\left\langle {111} \right\rangle\) 6°, в разные моменты времени в процессе нагревания. Структура малоугловых границ наклона представляет собой, как известно, набор геометрически необходимых зернограничных дислокаций (при отсутствии дополнительных внесенных дефектов). На рис. 4, а изображена стартовая структура расчетной ячейки, ядра зернограничных дислокаций хорошо различимы: это периодически расположенные вдоль границ небольшие области нарушения порядка кристаллической структуры (атомы белого цвета). Для угла разориентации 6° расстояние между дислокациями достаточно большое и хорошо видно, что структура между ними кристаллическая без каких либо нарушений. Разрушение кристаллической структуры при плавлении начиналось именно с ядер дислокаций (рис. 4, б). Инициация плавления при нагреве происходила при большей температуре, чем в случае большеугловой границы. При дальнейшем повышении температуры некоторые аморфные области росли быстрее, объединялись и распространялись в итоге на весь объем.

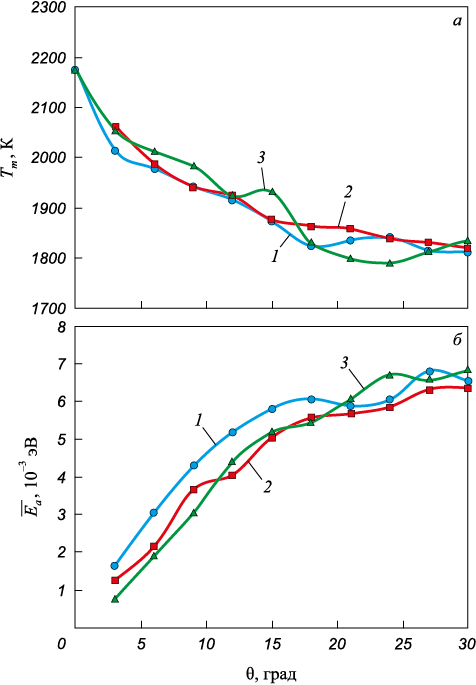
На рис. 5, а показана зависимость температуры плавления расчетной ячейки T_m от угла разориентации θ для всех рассмотренных границ зерен. Полученные зависимости оказались идентичными для всех трех рассмотренных осей разориентации границ \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) и \(\left\langle {111} \right\rangle\). Следует подчеркнуть, что специальные углы разориентации, то есть углы, для которых характерна высокая плотность совпадения структур зерен, в настоящем исследовании не рассматривались.

С ростом угла разориентации θ в области малых углов (менее 15°) температура плавления падает почти линейно, для большеугловых границ снижение становится менее интенсивным. Приведенные зависимости T_m(θ) коррелируют c энергией образования границы зерен или со связанной с ней величиной избыточной энергии расчетной ячейки. На рис. 5, б показаны зависимости избыточной энергии Δ\(\overline {{E_a}}\), приходящейся на один атом, от угла разориентации θ. Эта избыточная энергия определялась как разность средних значений потенциальной энергии атома в расчетной ячейке, содержащей пару рассматриваемых границ зерен, и в идеальном кристалле, содержащем столько же атомов.

Полученные зависимости Δ\(\overline {{E_a}}\)(θ) типичны для зависимостей энергии границ от угла разориентации [38 ‒ 40]. Сначала, примерно до значения θ = 15° (то есть для малоугловых границ), наблюдается почти линейный рост энергии: это обусловлено тем, что линейно растет плотность зернограничных дислокаций. При больших углах (примерно больше 15°) ядра дислокаций сливаются в один общий дефект и энергия растет с увеличением θ менее интенсивно.

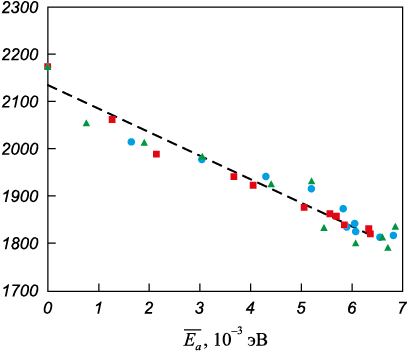
Между величинами T_m и Δ\(\overline {{E_a}}\), благодаря приведенным зависимостям, можно заметить корреляцию. Чтобы убедиться в этом, построили зависимость T_m(Δ\(\overline {{E_a}}\)) (рис. 6). Полученная зависимость в рамках рассматриваемого диапазона значений Δ\(\overline {{E_a}}\), действительно, оказалась очень близка к линейной с уравнением аппроксимационной линии T_m = –49 828Δ\(\overline {{E_a}}\) + 2135 (показана штриховой линией).

Таким образом, можно сделать вывод, что главным количественным критерием, определяющим влияние дефектов на снижение температуры плавления, является избыточная энергия, то есть разность энергий рассматриваемой структуры и идеального кристалла, которую еще можно интерпретировать как энергию образования рассматриваемой структуры или энергию, которая может потенциально выделиться при трансформации структуры, например, при рекристаллизации. Линейная зависимость объясняется, по всей видимости, тем, что избыточная энергия – показатель того, насколько ниже будет работа, которую нужно затратить на разрушение кристаллической решетки при плавлении, или, другими словами, насколько ниже будет теплота плавления рассматриваемого материала.

Выводы

С помощью молекулярно-динамического моделирования проведено исследование влияния угла разориентации и энергии границ зерен наклона с осями разориентации \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) и \(\left\langle {111} \right\rangle\) на температуру плавления и характер начальной инициации плавления на границе зерен в аустените. Показано, что при постепенном нагревании плавление начинается от границ зерен, там, где имеются нарушения кристаллической структуры и, соответственно, атомы находятся в менее глубоких потенциальных ямах. В случае большеугловых границ плавление начинается одновременно вдоль всей границы, в случае малоугловых ‒ в ядрах зернограничных дислокаций. Получены зависимости температуры плавления моделируемых расчетных ячеек от угла разориентации зерен и избыточной энергии. Для осей разориентации \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) и \(\left\langle {111} \right\rangle\) результаты оказались аналогичными. В области малых углов разориентации (менее 15°) температура плавления с ростом угла падает почти линейно, затем, для большеугловых границ, снижение становится менее интенсивным. Эти зависимости коррелируют c энергией образования границ зерен или со связанной с ней величиной избыточной энергии расчетной ячейки. Главным количественным критерием, определяющим влияние дефектов на снижение температуры плавления, является избыточная энергия, то есть разность энергий рассматриваемой структуры и идеального кристалла, которую еще можно интерпретировать как энергию образования рассматриваемой структуры. Температура плавления линейно уменьшается с ростом избыточной энергии. Очевидно, что данный эффект, то есть влияние границ зерен на температуру плавления, становится существенным только для материалов с очень высоким содержанием границ зерен, например, для материалов с нанокристаллической структурой.