Initiation of melting at tilt grain boundaries in austenite depending on the misorientation angle

Introduction

In recent decades, considerable attention has been paid to nanocrystalline materials, which include polycrystals with an average grain size of less than 100 nm. These materials exhibit size-dependent physical and mechanical properties, primarily due to a significantly higher volume fraction of grain boundaries, triple junctions, and other defects compared to conventional coarse-grained counterparts [1 ‒ 3]. Ultrafine grain sizes are achieved using various methods, which typically include severe plastic deformation. Such materials can also be produced by sintering nanopowders, vapor-phase condensation, or other nanostructuring methods. A characteristic feature of nanocrystalline materials is their highly non-equilibrium structure, associated with a significant level of excess (or stored) energy [1 ‒ 3]. Excess energy, i.e., the difference between the free energy of the material and that of an ideal crystal at the same temperature (or, in other words, the energy that can potentially be released during structural transformations such as recrystallization), in nanocrystalline materials arises from the high density of defects: grain boundaries, triple junctions, dislocations, disclinations, and others. The specific set and types of defects largely depend on the method used to produce the nanocrystalline structure and the subsequent treatment [1 ‒ 4].

The unique properties of nanomaterials are largely determined by the high volume fraction of surface area and other interfaces (interphase or intergranular boundaries). One of these properties, which is important from both an application and manufacturing standpoint, is the dependence of melting temperature on effective size: grain size, film thickness, or nanoparticle diameter. The dependence of the melting point of nanoparticles on their size is the most thoroughly studied. It is currently well established that the melting temperature of spherical nanoparticles is inversely proportional to their diameter, a finding demonstrated both experimentally [5 – 9] and through molecular dynamics (MD) simulations [10 – 14], as well as supported by theoretical models [15 ‒ 20].

As for materials with a nanocrystalline structure, studies [21 – 25] employing MD simulations have shown that melting in such materials is not a homogeneous process: it usually starts from free surfaces and grain boundaries. A reduction in the average grain size leads to a decrease in the melting temperature of nanocrystalline silver [22; 23] and aluminum [24; 25]. Similar findings were reported in [14; 26], where nanocrystalline nickel particles exhibited a lower melting point compared to monocrystalline counterparts.

The phenomenon of melting point reduction as a function of average grain size in nanocrystalline materials, in comparison with monocrystalline nanoparticles, is more complex and less thoroughly understood. This complexity arises from the presence of not a single type of defect (such as particle surfaces), but rather a broad spectrum of grain boundaries with varying energies, along with other structural defects. This study investigates the influence of the misorientation angle and the corresponding energy of tilt grain boundaries on the melting temperature and the mechanism of melting initiation at the boundary. Tilt boundaries with misorientation axes \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) and \(\left\langle {111} \right\rangle\) are examined. Austenite is chosen as the model material due to its widespread practical applications.

Model description

To describe interatomic interactions in the molecular dynamics model, an embedded atom method (EAM) potential was employed [27]. This potential was developed based on comparisons with experimental data and ab initio calculations of various properties of austenite. It reliably reproduces a wide range of mechanical and structural-energetic properties and has been successfully validated in simulations of various processes, including melting [27 ‒ 29].

The calculation cells had a parallelepiped shape with approximate dimensions of 9.9×10.8×13.5 nm and contained about 118,000 atoms (Fig. 1). A tilt grain boundary was introduced at the center of the calculation cell by rotating two crystals, i.e., the two halves of the cell, by a misorientation angle θ around the \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) and \(\left\langle {111} \right\rangle\) axis, which coincided with the x-axis in Fig. 1. To keep the grain boundary positioned at the center of the calculation cell throughout the simulation, fixed boundary conditions were applied along the z-axis (at the top and bottom of the calculation cell in Fig. 1): atoms shown in dark gray remained stationary during the simulation. Periodic boundary conditions were applied along the other directions. As a result, two parallel, identical grain boundaries were present in the calculation cell. Fig. 1 shows an example of the calculation cell visualized using the Common Neighbor Analysis (CNA) method [30], highlighting the presence of two boundaries – one in the center and one at the edge of the cell – with a misorientation axis of \(\left\langle {111} \right\rangle\) and a misorientation angle of 30° (hereafter referred to as \(\left\langle {111} \right\rangle\) 30°). After the rotation of the crystals and the removal of overlapping atoms, the structure was relaxed for 20 ps at a constant temperature of 1000 K. During relaxation, atoms shifted into positions corresponding to the local energy minimum. Fig. 1 shows the calculation cell after structural relaxation.

The misorientation angle θ for the \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) and \(\left\langle {111} \right\rangle\) grain boundaries was varied from 0° to 30°. Thus, half of the boundaries considered (up to 15°) corresponded to small-angle grain boundaries, i.e., boundaries with clearly distinguishable geometrically necessary grain-boundary dislocations, while the other half (above 15°) represented large-angle grain boundaries. As will be shown below, the main characteristic influencing the melting process is the grain boundary energy, which is typically nearly constant for large-angle boundaries. This is why, for example, most angles between boundaries at triple junctions tend to be close to 120° [31; 32]. For this reason, the misorientation angle was limited to 30° for all types of tilt boundaries considered in the present study.

The model employed an NPT ensemble in combination with a Nosé–Hoover thermostat. During melting, the specific volume increases due to the destruction of the crystal lattice; therefore, it was important to maintain constant pressure at zero. Thermal expansion with increasing temperature was taken into account, including for the fixed regions at the boundaries of the calculation cell (the dark gray regions in Fig. 1). A time integration step of 2 fs was used in the molecular dynamics simulations.

To determine the melting temperature, the gradual heating method was applied, involving the construction of dependence of the average atomic potential energy on temperature – a commonly used approach in similar studies [10 ‒ 14; 26; 33 ‒ 35]. The temperature was increased linearly at a rate of 10¹² K/s by correspondingly scaling the magnitudes of atomic velocities at regular time intervals (5 ps in this case).

Results and discussion

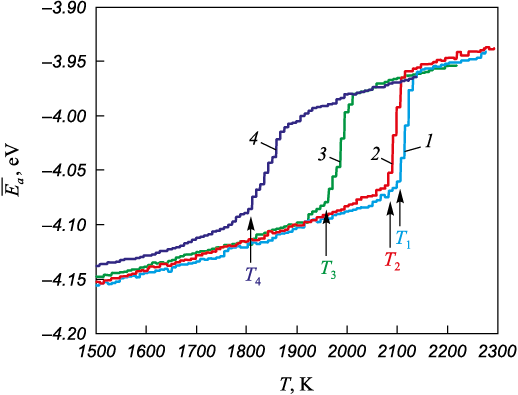
Fig. 2 shows examples of the dependencies of the average atomic potential energy on temperature for calculation cells with \(\left\langle {111} \right\rangle\) 6° (curve 3) and \(\left\langle {111} \right\rangle\) 30° (curve 4) grain boundaries, as well as for monocrystalline austenite (curves 1 and 2), during gradual heating at a rate of 10¹² K/s in the range from 1500 to 2300 K. As the temperature increases, the average atomic energy within the same phase increases almost linearly due to enhanced thermal vibrations of the atoms and thermal expansion. A sharp rise in the average atomic energy on the plots corresponds to a phase transition, i.e., melting.

As previously noted, the structure in the fixed boundary regions (Fig. 1) remained crystalline even after melting, which clearly affects the melting behavior and temperature of the entire calculation cell. Nevertheless, the use of fixed boundaries was necessary to preserve the grain boundaries with the initially assigned characteristics within the cell throughout the simulation. For monocrystalline austenite, i.e., a calculation cell without any defects, an additional analysis was carried out to evaluate the influence of fixed boundaries on the melting temperature. Fig. 2 presents the temperature dependence of the average atomic energy for the monocrystal: with fixed boundaries (curve 1) and with periodic boundaries on all sides (curve 2). As can be seen, melting in the presence of fixed boundaries indeed occurred at a higher temperature compared to the case with fully periodic boundary conditions. However, this difference was minor and had little effect on the qualitative results of the study.

In the presence of grain boundaries within the calculation cell, melting proceeded heterogeneously, meaning that it was initiated at the grain boundary, after which the solid–liquid front advanced from the boundary toward the center of the grains at a finite velocity, which is known to depend on temperature. The velocity was on the order of several tens of meters per second [36; 37]. Static two-phase coexistence, i.e., the simultaneous presence of part of the calculation cell in the liquid state and another part in the crystalline state for a relatively long period, was not observed: the solid–liquid front consistently advanced in one direction or another. Therefore, the melting temperature was determined based on the onset of the phase transition (indicated by arrows in Fig. 2), which in turn was identified as the intersection point of the linear approximations before and after the start of melting.

Fig. 2 clearly shows that the calculation cell containing a large-angle \(\left\langle {111} \right\rangle\) 30° grain boundary melts at a significantly lower temperature (1835 K) than the one with the small-angle \(\left\langle {111} \right\rangle\) 6° boundary (2013 K), confirming the influence of grain boundary type on melting behavior. The grain boundary energy, and consequently the degree of disruption of the crystalline structure, is higher in the case of the large-angle boundary.

Fig. 3 shows a calculation cell in the yz-plane containing two large-angle \(\left\langle {111} \right\rangle\) 30° boundaries at different stages of melting, visualized using a structure identification tool based on the Common Neighbor Analysis (CNA) method [30]. This method allows each atom to be classified according to its local crystalline environment by analyzing the arrangement of its neighboring atoms. In the present case, an atom was considered to belong to an FCC lattice if more than 75 % of its nearest neighbors were located near the lattice sites of an ideal FCC crystal (taking into account thermal expansion), within a tolerance of 25 % of the first coordination sphere radius. Atoms that did not satisfy these conditions, or the conditions for classification as HCP, were considered to be part of an amorphous structure (shown in white in Fig. 3).

Fig. 3, a shows the relaxed initial structure of the calculation cell with two parallel \(\left\langle {111} \right\rangle\) 30° boundaries. In the case of a large-angle boundary, the defect appears almost continuous: disruption of the crystalline structure is observed along the entire boundary. As the temperature increased, melting began almost uniformly along the boundary (Fig. 3, b), except near the fixed boundaries (at the top and bottom of the calculation cell), which is expected, as the influence of the constrained crystalline structure at those boundaries becomes significant in those regions.

With further temperature increase, the solid–liquid front propagated from the grain boundaries into the bulk of the material (Fig. 3, c). The number of atoms in the amorphous phase (shown in white) increased accordingly. It can be observed that melting initiation at the boundary occurred even at a lower temperature than the melting point determined from the energy – temperature plot for the entire calculation cell (Fig. 2). This is due to the fact that the melting temperature of the entire calculation cell is influenced by the grain boundary density. A similar dependence was observed in [22 ‒ 25] as the average grain size in nanocrystalline silver or aluminum decreased, the melting temperature also decreased. In the present case, this implies that, for example, an increase in the size of the cell along the y-axis would reduce the influence of the grain boundary on the overall melting temperature.

Melting initiates at grain boundaries because the crystalline structure is more easily disrupted in their vicinity. This occurs because atoms located in defect regions are situated in shallower potential wells compared to those in a perfect crystal, and can escape more easily due to thermal vibrations. Atoms located near the solid–liquid interface on the crystalline side are also found in relatively shallow potential wells, as the atomic arrangement on the molten side is more disordered. In addition, the melt exhibits more intense self-diffusion and a greater amount of free volume compared to the crystal. These factors also contribute to easier disruption of the crystal structure near the interface than within the bulk of the crystal, and thus drive the motion of the solid–liquid front.

Fig. 4 shows a calculation cell containing two small-angle \(\left\langle {111} \right\rangle\) 6° grain boundaries at different time pointsduring the heating process. The structure of small-angle tilt boundaries is known to consist of an array of geometrically necessary grain-boundary dislocations, provided that no additional defects are introduced. Fig. 4, a displays the initial structure of the calculation cell, where the cores of the grain-boundary dislocations are clearly visible. These appear as small regions of disrupted crystalline order (white atoms) periodically arranged along the boundaries. For a misorientation angle of 6°, the distance between dislocations is sufficiently large, and it is clearly seen that the structure between them remains fully crystalline, with no visible disorder. Melting initiated from the dislocation cores (Fig. 4, b) as the crystalline structure began to break down. In this case, melting began at a higher temperature compared to that observed for the large-angle grain boundary. As the temperature continued to increase, some amorphous regions grew more rapidly, merged, and eventually spread throughout the entire volume.

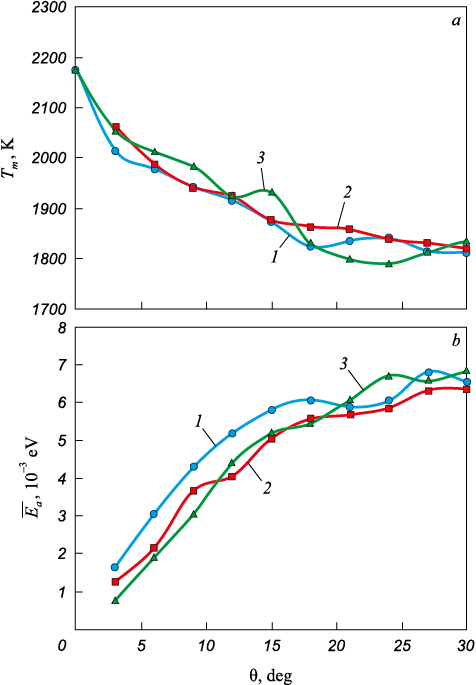
Fig. 5, a shows the dependences of the melting point T_m of the calculation cell on the misorientation angle θ for all grain boundaries considered in the study. The resulting dependences were identical for all three grain boundary misorientation axes \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) and \(\left\langle {111} \right\rangle\). It should be noted that special misorientation angles, i.e., those characterized by a high degree of atomic coincidence between adjacent grains, were not considered in this study.

As the misorientation angle θ increases in the low-angle range (less than 15°), the melting point decreases almost linearly. For large-angle grain boundaries, the decrease becomes less pronounced. The obtained T_m(θ) dependences correlate with the grain boundary energy or with the associated value of excess energy of the calculation cell. Fig. 5, b shows the dependences of the excess energy per atom Δ\(\overline {{E_a}}\), on the misorientation angle θ. This excess energy was calculated as the difference between the average potential energy per atom in a calculation cell containing a pair of the studied grain boundaries, and that in an ideal crystal containing the same number of atoms.

The obtained Δ\(\overline {{E_a}}\)(θ) dependences are typical of the angular dependences of grain boundary energy [38 – 40]. Initially, up to approximately θ = 15° (i.e., for small-angle grain boundaries), the excess energy increases almost linearly, which is due to the linear increase in the density of grain-boundary dislocations. At larger misorientation angles (above ~15°), the dislocation cores merge into a single extended defect, and the energy increases more slowly with increasing θ.

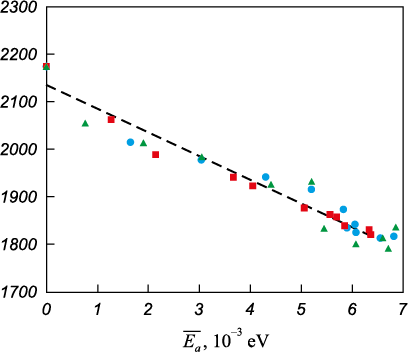
The obtained dependencies   indicate a correlation between T_m and Δ\(\overline {{E_a}}\). To verify this, the T_m(Δ\(\overline {{E_a}}\)) dependence was plotted (Fig. 6). Within the studied range of Δ\(\overline {{E_a}}\), values, the relationship is approximately linear and follows the equation T_m = –49,828Δ\(\overline {{E_a}}\) + 2,135 (shown as a dashed line).

Thus, it can be concluded that the main quantitative criterion determining the influence of defects on the reduction of the melting point is the excess energy – that is, the difference between the energy of the structure under consideration and that of an ideal crystal. This quantity can also be interpreted as the formation energy of the given structure or as the energy potentially released during structural transformation, such as recrystallization. The observed linear dependence is likely due to the fact that the excess energy reflects the reduction in work required to break the crystal lattice during melting – or, put differently, the corresponding decrease in the material’s heat of fusion.

Conclusions

Molecular dynamics simulations were used to investigate the effect of the misorientation angle and grain boundary energy of tilt boundaries with misorientation axes \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) and \(\left\langle {111} \right\rangle\) on the melting temperature and the nature of melting initiation at grain boundaries in austenite. The results show that during gradual heating, melting begins at the grain boundaries, where the crystal structure is disrupted and atoms are located in shallower potential wells. For large-angle boundaries, melting is initiated simultaneously along the entire boundary, whereas for small-angle boundaries, it starts at the cores of grain-boundary dislocations. Dependences of the melting temperature of the simulated calculation cells on the grain misorientation angle and excess energy were obtained. Similar results were observed for the \(\left\langle {100} \right\rangle\), \(\left\langle {110} \right\rangle\) and \(\left\langle {111} \right\rangle\) misorientation axes. In the range of low misorientation angles (less than 15°), the melting point decreases almost linearly as the angle increases. For large-angle boundaries, the decrease becomes less pronounced. These dependences correlate with the grain boundary energy or the corresponding excess energy of the calculation cell. The key quantitative parameter determining the influence of defects on the reduction of the melting point is the excess energy – that is, the difference between the energy of the structure under consideration and that of an ideal crystal. This value can also be interpreted as the formation energy of the given structure. A linear decrease in melting point with increasing excess energy was observed. It is clear that this effect – the influence of grain boundaries on the melting point – becomes significant only in materials with a very high content of grain boundaries, such as those with a nanocrystalline structure.