Перейти к:
Математическая модель состояния футеровки главного желоба доменной печи
https://doi.org/10.17073/0368-0797-2025-4-411-416
Аннотация
Главный горновой желоб доменной печи – это сложная технологическая конструкция, играющая критическую роль в процессе выплавки чугуна. Он служит для отвода расплавленного чугуна и шлака из горна печи, обеспечивая непрерывность и безопасность процесса. Надежная работа желоба напрямую влияет на производительность доменной печи. Конструкция желоба должна выдерживать экстремально высокие температуры и агрессивную химическую среду, а его правильное функционирование требует постоянного контроля и обслуживания. Корректный выбор огнеупорных материалов, технологии футерования, а также выявление возможности повышения стойкости огнеупорной футеровки главных горновых желобов и продления срока их службы определены своевременным получением информации о тепловой нагрузке на слои огнеупоров и кожух, об условиях эксплуатации, конструктивных особенностях и процессах разрушения огнеупоров при их взаимодействии с чугуном и шлаком. Системы контроля работы главного горнового желоба доменной печи призваны обеспечивать безопасную и эффективную его эксплуатацию, своевременно выявляя отклонения от нормального режима и предотвращая аварийные ситуации. Они включают в себя визуальный, инструментальный и автоматический контроль. Система мониторинга разгара главных горновых желобов позволит технологическому персоналу доменной печи контролировать состояние желобов, оценивать их остаточный ресурс и принимать своевременные решения об их ремонте. Разработанная математическая модель состояния футеровки главного желоба доменной печи учитывает термоконтроль кожухов горновых желобов в реальном времени. Она нацелена на получение оперативной информации по разгару главных горновых желобов и основана на решении задачи стационарной теплопроводности многослойной плоской стенки, каждый слой которой является однородной стенкой.
Ключевые слова
Для цитирования:
Дмитриев А.Н., Витькин Д.А., Золотых М.О., Витькина Г.Ю. Математическая модель состояния футеровки главного желоба доменной печи. Известия высших учебных заведений. Черная Металлургия. 2025;68(4):411-416. https://doi.org/10.17073/0368-0797-2025-4-411-416
For citation:
Dmitriev A.N., Vit’kin D.A., Zolotykh M.O., Vit’kina G.Yu. Mathematical model of the blast furnace main trough lining condition. Izvestiya. Ferrous Metallurgy. 2025;68(4):411-416. https://doi.org/10.17073/0368-0797-2025-4-411-416
Введение
Система выпускных желобов доменной печи обычно включает главный желоб и разливочные желоба, при этом в главном желобе происходит отделение чугуна от шлака, в связи с чем он находится в наиболее тяжелых условиях. По этой причине совершенствованию его футеровки уделяют наибольшее внимание как изготовители огнеупорных материалов, так и потребители.
Количество имеющихся литературных данных, связанных с изучением теплообмена в футеровке главного горнового желоба, значительно меньше, чем данных, связанных с футеровкой внутри доменной печи. Однако в последние годы информация из иностранной литературы позволяет оценить усилия, приложенные для изучения данной проблематики.
В научных работах, посвященных исследованию разделения чугуна и шлака в главных желобах доменных печей, использовался широкий спектр методик, сочетающих экспериментальные и численные подходы [1 – 3]. Экспериментальные исследования, такие как в работах [4; 5], были проведены с помощью физического моделирования, при этом применялись аналогичные жидкости (например, масло и вода для имитации чугуна и шлака) для изучения влияния геометрических параметров желоба (угол наклона, форма поперечного сечения) и скорости выпуска расплава на эффективность разделения фаз. В работе [5], в частности, использована масштабная модель 1:10 для верификации результатов численного моделирования.
Численное моделирование играет ключевую роль в исследовании сложных процессов тепло- и массопереноса в желобе [6 – 9]. Исследователи применяли различные подходы к численному моделированию, такие как метод конечных объемов [7] и метод конечных элементов [8 – 11]), решая уравнения Навье-Стокса для описания гидродинамики потока и уравнения теплопроводности (с учетом излучения [11 – 13]) для моделирования температурного поля. Учтены факторы, влияющие на эффективность разделения и срок службы футеровки: турбулентность потока [7; 9], теплообмен между расплавом и огнеупором [14 – 17], тепловое излучение [10; 12; 13] и износ огнеупора [10]. В работе [7], например, была использована k–ε модель турбулентности, а в работах [10; 13] применялись нелокальные граничные условия для учета теплового излучения. В работе [8] авторы сосредоточили внимание на определении критических изотерм для повышения срока службы футеровки, используя двумерную модель теплообмена и сопоставляя результаты моделирования с экспериментальными данными. В работе [10] показано, что возможно применение разработки адаптивного регулятора шага времени для эффективного моделирования длительных циклов работы доменной печи.
Полученные результаты численного моделирования в большинстве случаев хорошо коррелировали с экспериментальными данными, позволяя выявлять области с максимальными температурами и напряжениями в футеровке [14 – 17], чаще всего в боковых стенках, и прогнозировать ее износ. Однако необходимо отметить наличие некоторой неопределенности, связанной, например, с точным расположением термопар для измерения температуры в работающем желобе [18 – 20], что требует применения дополнительных методов обработки данных (например, гибридный алгоритм GRSA [10]) для уточнения результатов. В целом, сочетание экспериментальных и численных методов позволило получить более полное представление о сложных процессах, происходящих в главных желобах доменных печей, и создать основу для разработки рекомендаций по оптимизации их конструкции и эксплуатации.
Исходные данные
Данная работа посвящена разработке математической модели огнеупорной футеровки главного желоба доменной печи, проводимой в Институте металлургии УрО РАН. Представлен алгоритм расчета температурного поля в огнеупорной футеровке желоба на основании показаний термопар, установленных на внешней стороне металлического кожуха желоба.
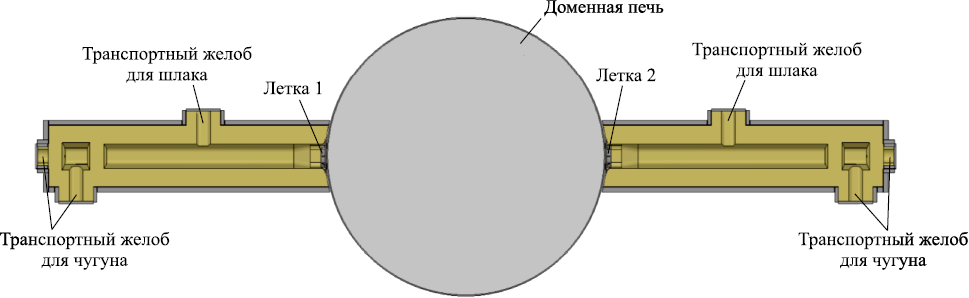
На рис. 1 представлен общий вид (условно) сверху двух главных желобов доменной печи.
Рис. 1. Главные горновые желоба доменной печи |
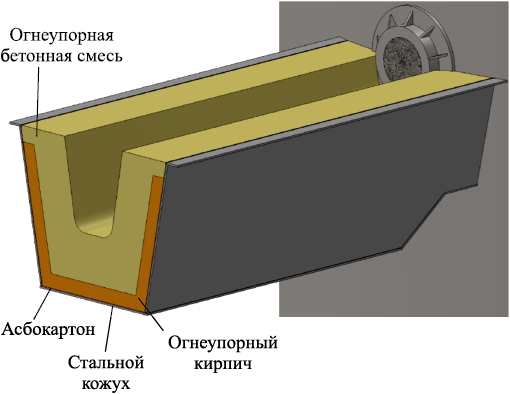
Футеровка главного горнового желоба в поперечном сечении представлена на рис. 2.
Рис. 2. Слои футеровки главного желоба в поперечном сечении |
Расчет теплопроводности через многослойную плоскую стенку
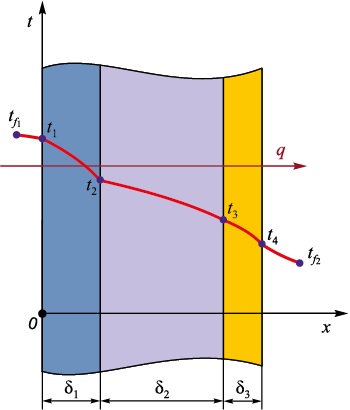
Решение данной задачи сводится к стационарной теплопроводности многослойной плоской стенки, каждый слой которой является однородной стенкой. Предполагается, что общая толщина многослойной стенки, равная сумме толщин отдельных слоев, намного меньше высоты и ширины стенки. В этом случае изотермическими поверхностями являются плоскости, параллельные граничным плоскостям (в том числе и плоскости стыка между отдельными слоями). Отдельные слои стенки имеют гладкие граничные поверхности, плотно прилегающие друг к другу так, что температуры контактирующих поверхностей равны (рис. 3).
Рис. 3. Многослойная плоская стенка: |
При рассмотрении теплопроводности однослойной стенки видно, что плотность теплового потока не изменяется при переходе от одной изотермической поверхности к другой при движении слева направо, т. е. вдоль оси х.
Плоскость стыка между первым и вторым слоями также представляет собой изотермическую поверхность с тем же значением плотности теплового потока, что и в первом слое. Но эта плоскость является «начальной» по отношению ко второму слою, в котором, следовательно, также установится постоянная по толщине плотность теплового потока q, равная плотности теплового потока в первом слое. Такие же рассуждения справедливы и для всех последующих слоев.
Тепловой поток и, соответственно, его плотность не изменяются по толщине плоской стенки (Q ≠ f (x) и q ≠ f (x)) и поэтому для любого i-го слоя многослойной плоской стенки можно написать
| \[{q_s} = \frac{{\Delta {T_i}}}{{\frac{{{\delta _i}}}{{{\lambda _i}}}}} = {\rm{const}}.\] | (1) |
Запишем это выражение последовательно для всех слоев, начиная с первого:
| \[{q_s} = \frac{{{T_{{f_1}}} - {T_1}}}{{\frac{1}{{{\alpha _1}}}}} = \frac{{{T_1} - {T_2}}}{{\frac{{{\delta _1}}}{{{\lambda _1}}}}} = \frac{{{T_2} - {T_3}}}{{\frac{{{\delta _2}}}{{{\lambda _2}}}}} = \frac{{{T_3} - {T_4}}}{{\frac{{{\delta _3}}}{{{\lambda _3}}}}} = \frac{{{T_4} - {T_{{f_2}}}}}{{\frac{1}{{{\alpha _2}}}}}.\] | (2) |
Преобразуем полученные выражения в формат \(q\frac{1}{{{\alpha _1}}} = {T_{{f_1}}} - {T_2}\) и сложим полученные выражения (левые части с левыми, а правые – с правыми):
\[q\left( {\frac{1}{{{\alpha _1}}} + \frac{{{\delta _1}}}{{{\lambda _1}}} + \frac{{{\delta _2}}}{{{\lambda _2}}} + \frac{{{\delta _3}}}{{{\lambda _3}}} + \frac{1}{{{\alpha _2}}}} \right) = {T_{{f_1}}} - {T_{{f_2}}}.\]
Данные выкладки справедливы и для большего количества слоев. Таким образом, в общем виде формула поверхностной плотности теплового потока (qs ) выглядит следующим образом:
| \[{q_s} = \frac{{{T_{{f_1}}} - {T_{{f_2}}}}}{{\frac{1}{{{\alpha _1}}} + \sum\limits_{i = 1}^n {\left( {\frac{{{\delta _i}}}{{{\lambda _i}}} + \frac{1}{{{\alpha _2}}}} \right)} }},\] | (3) |
где α1 , α2 – коэффициенты теплоотдачи от горячего флюида к стенке и от стенки к холодному флюиду соответственно, Вт/(м2·К); λ – коэффициент теплопроводности материала, Вт/(м·К).
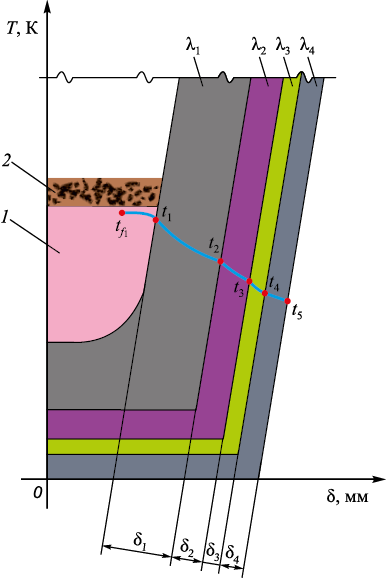
На рис. 4 представлена схема теплопередачи для главного желоба доменной печи.
Рис. 4. Схема теплопередачи главного желоба: |
Контроль температуры осуществляется по термопарам, которые расположены на кожухе главного желоба. Футеровка главного желоба состоит из трех слоев огнеупорных материалов и заканчивается сталью кожуха, поэтому в данном случае формула поверхностной плотности теплового потока принимает вид:
| \[{q_l} = \frac{{{T_{{f_1}}} - {T_5}}}{{\frac{1}{{{\alpha _1}}} + \frac{{{\delta _1}}}{{{\lambda _1}}} + \frac{{{\delta _2}}}{{{\lambda _2}}} + \frac{{{\delta _3}}}{{{\lambda _3}}} + \frac{{{\delta _4}}}{{{\lambda _4}}}}},\] | (4) |
где \({T_{{f_1}}}\) – температура горячего флюида (чугун, шлак), К; Т5 – температура кожуха, контролируемая термопарой (теплосъем может идти с дискретностью от 10 с до 24 ч), К; α1 – коэффициент теплоотдачи от горячего флюида к внутренней стенке желоба, Вт/(м2·К); δ1 , δ2 , δ3 , δ4 – толщина слоя огнеупорного материала от внутреннего к наружному соответственно, м; λ1 , λ2 , λ3 , λ4 – коэффициент теплопроводности огнеупорных материалов от внутреннего к наружному соответственно, Вт/(м·К).
В областях сопряжения теплофизические характеристики материалов усредняются.
Блок-схема алгоритма расчета
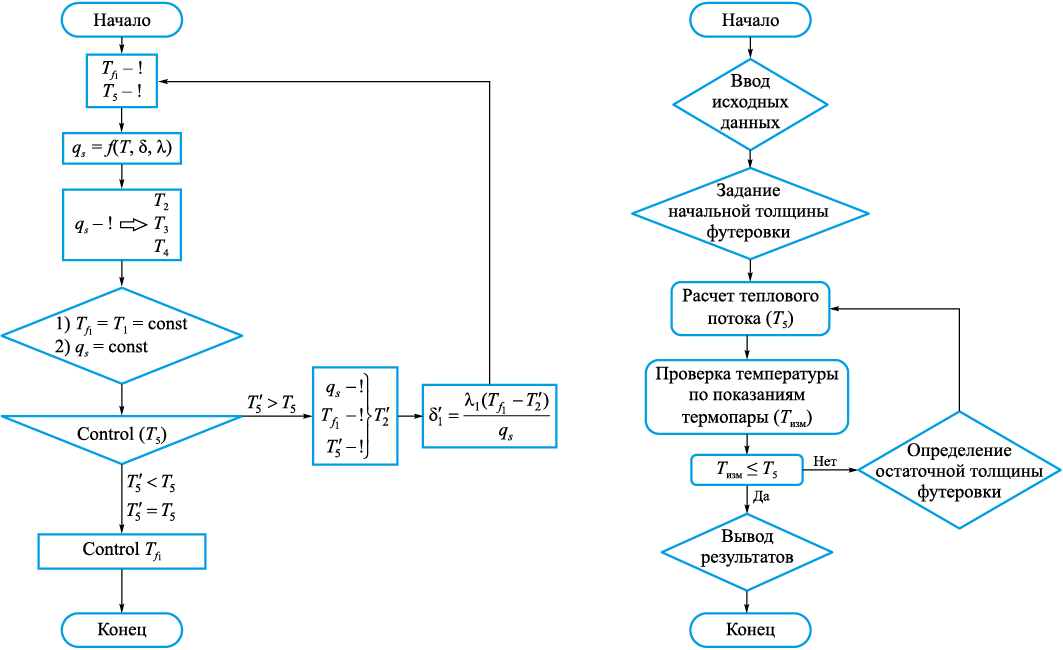
Блок-схема алгоритма расчета изменения температуры по слоям футеровки приведена на рис. 5.
Рис. 5. Блок-схема и диаграмма алгоритма расчета изменения температуры |
Выводы
Разработанная математическая модель состояния футеровки главного желоба доменной печи, основанная на решении задачи стационарной теплопроводности многослойной стенки, позволяет эффективно оценивать тепловую нагрузку на каждый слой огнеупоров и кожух в реальном времени (согласно настроенной дискретности теплосъема). Это обеспечивает оперативный контроль за состоянием футеровки, прогнозирование ее остаточного ресурса (толщины внутреннего слоя) и своевременное принятие решений о ремонте или замене, что напрямую способствует повышению эффективности и безопасности эксплуатации доменной печи, минимизируя риски аварийных ситуаций и увеличивая срок службы футеровки. Дальнейшие исследования будут направлены на усовершенствование модели, например, путем учета нестационарных тепловых процессов (ввода времени в модель), а также более сложных геометрических форм желоба.
Список литературы
1. Ranjan S., Mazumdar D., Chakraborty I.N., Sinha S., Sarkar R. Review and analysis of metallurgical processes in blast furnace main trough and trough performances. Transactions of the Indian Institute of Metals. 2022;75:589–611. https://doi.org/10.1007/s12666-021-02454-9
2. Kostúr K. Mathematical model for optimisation of a thickness of furnace lining. In: 18th Int. Carpathian Control Conf. (ICCC). 2017:52–57. https://doi.org/10.1109/CarpathianCC.2017.7970370
3. Prompt N., Ouedraogo E. High temperature mechanical characterisation of an alumina refractory concrete for Blast Furnace main trough: Part I. General context. Journal of the European Ceramic Society. 2008;28(15):2859–2865. https://doi.org/10.1016/j.jeurceramsoc.2008.04.031
4. Kim H., Ozturk B., Fruehan R.J. Slag-metal separation in the blast furnace trough. ISIJ International. 1998;38(5):430–439. https://doi.org/10.2355/isijinternational.38.430
5. Monteiro de Oliveira M.J., Rodrigues G., Alves da Silva I., Peixoto J.J.M., da Silva C.A. Modeling of two‐phase flow in blast furnace trough. Steel Research International. 2021;92(3):2000485. https://doi.org/10.1002/srin.202000485
6. Rezende R.V.P., Silva A.F.C., Maliska C.R. The blast furnace trough two-phase flow and its influence in the refractory lining wear: Mathematical modeling and numerical simulation. In: Proceedings of the 19th Int. Congress of Mechanical Engineering. 2007.
7. Ge Y., Li M., Wei H., Liang D. Numerical analysis on velocity and temperature of the fluid in a blast furnace main trough. Processes. 2020;8(2):249. https://doi.org/10.3390/pr8020249
8. Vázquez-Fernández S., Pieiga A.G.L., Lausín-González C., Quintela P. Mathematical modelling and numerical simulation of the heat transfer in a trough of a blast furnace. International Journal of Thermal Sciences. 2019;137:365–374. https://doi.org/10.1016/j.ijthermalsci.2018.11.025
9. Yao H., Chen H., Ge Y., Wei H. Numerical analysis on erosion and optimization of a blast furnace main trough. Materials. 2021;14(17):4851. https://doi.org/10.3390/ma14174851
10. Barral P., Pérez-Pérez L.J., Quintela P. Numerical simulation of the transient heat transfer in a blast furnace main trough during its complete campaign cycle. International Journal of Thermal Sciences. 2022;173:107349. https://doi.org/10.1016/j.ijthermalsci.2021.107349
11. Barral P., Pérez-Pérez L.J., Quintela P. Transient 3D hydrodynamic model of a blast furnace main trough. Engineering Applications of Computational Fluid Mechanics. 2023;17(1):2280776. https://doi.org/10.1080/19942060.2023.2280776
12. Barral P., Nicolás B., Pérez-Pérez L.J., Quintela P. Numerical simulation of wear related problems in a blast furnace runner. Recent Advances in Differential Equations and Applications. 2019;18:229–244. https://doi.org/10.1007/978-3-030-00341-8_14
13. Barral P., Pérez-Pérez L.J., Quintela P. Transient thermal response with nonlocal radiation of a blast furnace main trough. Applied Mathematical Modelling. 2022;105: 197–225. https://doi.org/10.1016/j.apm.2021.12.029
14. Kou M., Yao S., Wu S., Zhou H., Xu J. Effects of blast furnace main trough geometry on the slag-metal separation based on numerical simulation. Steel Research International. 2019;90(2):1800383. https://doi.org/10.1002/srin.201800383
15. Wang L., Pan C.-N., Cheng W.-T. Numerical analysis on flow behavior of molten iron and slag in main trough of blast furnace during tapping process. Advances in Numerical Analysis. 2017;2017(1):713160. https://doi.org/10.1155/2017/6713160
16. Luomala M.J., Paananen T.T., Köykkä M.J., Fabritius J., Matti T., Nevala H., Härkki J.J. Modelling of fluid flows in the blast furnace trough. Steel Research. 2001;72(4): 130–135. https://doi.org/10.1002/srin.200100096
17. He Q., Evans G., Zulli P., Tanzil F., Lee B. Flow characteristics in a blast furnace trough. ISIJ International. 2002;42(8):844–851. https://doi.org/10.2355/isijinternational.42.844
18. He Q., Zulli P., Tanzil F., Lee B., Dunning J., Evans G. Flow characteristics of a blast furnace taphole stream and its effects on trough refractory wear. ISIJ International. 2002;42(3):235–242. https://doi.org/10.2355/isijinternational.42.235
19. Shao L., Saxén H. A simulation study of Blast furnace hearth drainage using a two-phase flow model of the taphole. ISIJ International. 2011;51(2):228–235. https://doi.org/10.2355/isijinternational.51.228
20. Li Z., Wang H., Ding F., Tang H. Prolonging campaign life of blast furnace trough by water cooling. Materials. 2023;16(3):891. https://doi.org/10.3390/ma16030891
Об авторах
А. Н. ДмитриевРоссия
Андрей Николаевич Дмитриев, д.т.н., главный научный сотрудник лаборатории пирометаллургии восстановительных процессов
Россия, 620016, Екатеринбург, ул. Амундсена, 101
Д. А. Витькин
Россия
Дмитрий Александрович Витькин, инженер-конструктор
Россия, 620078, Екатеринбург, ул. Мира, 33
М. О. Золотых
Россия
Максим Олегович Золотых, к.т.н., ведущий инженер лаборатории пирометаллургии восстановительных процессов
Россия, 620016, Екатеринбург, ул. Амундсена, 101
Г. Ю. Витькина
Россия
Галина Юрьевна Витькина, к.т.н., ведущий научный сотрудник, заведующий лабораторией пирометаллургии восстановительных процессов
Россия, 620016, Екатеринбург, ул. Амундсена, 101
Дополнительные файлы
Рецензия
Для цитирования:
Дмитриев А.Н., Витькин Д.А., Золотых М.О., Витькина Г.Ю. Математическая модель состояния футеровки главного желоба доменной печи. Известия высших учебных заведений. Черная Металлургия. 2025;68(4):411-416. https://doi.org/10.17073/0368-0797-2025-4-411-416
For citation:
Dmitriev A.N., Vit’kin D.A., Zolotykh M.O., Vit’kina G.Yu. Mathematical model of the blast furnace main trough lining condition. Izvestiya. Ferrous Metallurgy. 2025;68(4):411-416. https://doi.org/10.17073/0368-0797-2025-4-411-416
JATS XML