Перейти к:
Микрогетерогенное строение жидких чугунов ИЧХ28Н2, ИЧ310Х24М2Ф4ТР
https://doi.org/10.17073/0368-0797-2024-5-579-592
Аннотация
Приведены оригинальные экспериментальные данные о вязкости и удельном электросопротивлении жидких чугунов ИЧХ28Н2, ИЧ310Х24М2Ф4ТР. Результаты измерений рассмотрены в рамках представлений о микрогетерогенности металлических расплавов. Жидкий чугун в микрогетерогенном состоянии понимался как дисперсная система, состоящая из дисперсных частиц Fe – 30 % Cr, распределенных в дисперсионной среде Fe – 3 % C. Представления о коллоидной микронеоднородности (микрогетерогенности) расплавов Fe – C впервые сформулированы А.А. Вертманом и А.М. Самариным более 80 лет назад и нашли еще одно подтверждение в данной работе. Привнесение теоретических подходов реологии дисперсных систем в анализ температурных зависимостей вязкости микрогетерогенных расплавов позволило оценить параметры микрогетерогенности: объемную долю и их размер. Определение объемной доли дисперсных частиц проводилось по уравнению Тейлора для вязкости дисперсных систем и размера дисперсных частиц в рамках представлений теории абсолютных скоростей реакций. Анализ температурных зависимостей удельного электросопротивления микрогетерогенных расплавов в рамках теории явлений переноса (в данном случае проводимости) в неоднородных средах (микрогетерогенных расплавах) дал возможность оценки объемной доли дисперсных частиц. Объемную долю дисперсных частиц по данным об удельном электросопротивлении жидких чугунов определяли из уравнения Оделевского для проводимости неоднородных сред. Установлены размер кластера из соотношения величин удельного электросопротивления расплава при температуре ликвидус и температуре анализа с учетом известных данных для длины свободного пробега и коэффициент рассеяния электронов жидкого железа. Величина объемной доли дисперсных частиц в жидких чугунах составила 0,2 – 0,1 вблизи температуры ликвидус. С повышением температуры объемная доля дисперсных частиц уменьшается. Размер кластера в жидком чугуне составил около 3 нм вблизи температуры ликвидус, с повышением температуры размер кластера снижается до 1 – 2 нм. Полученные результаты имеют практическое значение: повышение эксплуатационных свойств отливок из чугунов возможно путем высокотемпературной обработки расплава (ВТОР) с целью изменения условий кристаллизации и получения модифицированной структуры. Исследования микрогетерогенного строения жидких чугунов и оценка параметров микрогетерогенности позволит обосновать и предложить оптимальный режим ВТОР с целью повышения эксплуатационных характеристик изделий из износостойких чугунов, легированных хромом.
Ключевые слова
Для цитирования:
Цепелев В.С., Синицин Н.И., Чикова О.А., Потапов М.Г., Вьюхин В.В. Микрогетерогенное строение жидких чугунов ИЧХ28Н2, ИЧ310Х24М2Ф4ТР. Известия высших учебных заведений. Черная Металлургия. 2024;67(5):579-592. https://doi.org/10.17073/0368-0797-2024-5-579-592
For citation:
Tsepelev V.S., Sinitsin N.I., Chikova O.A., Potapov M.G., V’yukhin V.V. Microheterogeneous structure of liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR. Izvestiya. Ferrous Metallurgy. 2024;67(5):579-592. https://doi.org/10.17073/0368-0797-2024-5-579-592
Введение
Развитие представлений о микронеоднородном строении металлических сложнолегированных расплавов с практической точки зрения актуально для научного обоснования выбора режима температурно-временной обработки. Обсуждение структурных переходов, связанных с необратимым разрушением микронеоднородностей при нагреве расплава до определенной для каждого состава температуры Т\(^*\), делает это обоснование возможным. Измерение температурных зависимостей вязкости, плотности, электросопротивления и поверхностного натяжения расплава позволяет определить температуру Т\(^*\), объяснив ее структурным переходом, обусловленным разрушением микронеоднородностей. Многочисленными экспериментами установлено, что после структурного перехода при последующем охлаждении и кристаллизации формируется слиток со структурой, подобной модифицированной, обладающий лучшими механическими характеристиками. Механизм структурных переходов в жидких сложнолегированных металлических расплавах заключается в разрушении микронеоднородности не только структуры, но и химического состава. Аномалии температурных и концентрационных зависимостей структурно чувствительных свойств металлических расплавов – вязкости, плотности, электросопротивления и поверхностного натяжения вызваны изменением структуры расплава. Микронеоднородности, которые возникают вследствие преобладающего взаимодействия односортных или разносортных атомов, соответствуют нарушению ближнего порядка в расположении атомов (SRO) и диапазону 2 – 5 Å. Микронеоднородное состояние металлических расплавов, которое обусловлено сегрегацией атомов флуктуационной природы без четких межфазных границ (кластерами), связано с нарушением среднего порядка (MRO) и диапазоном 5 – 20 Å. Микрогетерогенное состояние расплава, которое характеризуется наличием дисперсных частиц, обогащенных одним из компонентов, которые взвешены в окружающей среде иного состава с четкой межфазной поверхностью, соответствует нарушению дальнего порядка (LRO) и диапазону более 20 Å [1]. В работе [2] основное внимание уделяется изучению примесных эффектов, соответствующих SRO в сложнолегированных расплавах, в том числе проводятся исследования структуры и свойств расплавов на основе железа с целью использования для совершенствования технологий получения чугунов и сталей. С методологической точки зрения, наряду с прямым дифракционным исследованием структуры, здесь большой объем информации дают измерения таких физических свойств, как магнитная восприимчивость, удельное электросопротивление, вязкость, плотность. Например, магнитная восприимчивость вместе с удельным электросопротивлением составляет пару электронно-чувствительных свойств, которые позволяют оценить характер ближнего порядка в системе, распределение примесей и легирующие эффекты. Изучение всего комплекса свойств позволяет воздействовать на расплав, применяя малые добавки. Осциллирующий характер их влияния способствует достижению существенных эффектов при помощи малых изменений концентрации. Кроме того, появляется возможность управления структурой расплава и процессом первичной кристаллизации.
Представлены результаты расчета радиусов микрогруппировок вокруг атомов углерода в железе и электронных характеристик разбавленных сплавов Fe – C – O [2]. Представления о кластерном строении металлической жидкости, которое обусловлено сегрегацией атомов флуктуационной природы без четких межфазных границ (кластерами), связано с нарушением MRO и диапазоном 5 – 20 Å, последовательно развиваются Тягуновым Г.В. Кластерное строение металлической жидкости может быть описано в физических терминах, если известны количество, состав и размеры кластеров, число атомов, входящих в кластеры, время жизни кластеров и т. д., при этом кластеры обладают значительными размерами Rкл ≥ (10 – 25)·10\(^–\)10 м [3].
Представления о коллоидном, т. е. микрогетерогенном строении жидких расплавов, которое характеризуется наличием дисперсных частиц, обогащенных одним из компонентов, которые взвешены в окружающей среде иного состава с четкой межфазной поверхностью, соответствуют LRO и диапазону более 20 Å, в отношении эвтектических и монотектических расплавов последовательно развиваются Попелем П.С. [4]. Идея о коллоидном строении эвтектических расплавов впервые предложена Клячко Ю.А. [5], затем ее развивали Залкин В.М., Вертман А.А. и Самарин А.М. с сотрудниками [6 – 9]. Они рассматривали эвтектические расплавы как классические коллоидные системы с дисперсностью частиц порядка 1 – 10 нм. В таком случае, с точки зрения физической химии, расплав представляет собой микрогетерогенную систему. Термины «микрорасслоенное» и «коллоидное состояние» также используются в том же смысле. Залкин В.М. понимал эвтектические сплавы в жидком состоянии как термодинамически устойчивое двухфазное состояние (микроэмульсии), обусловленное замедленным растворением одного из компонентов, и постепенно переходящее в состояние истинного (гомогенного) раствора, т. е. как лиофильные двухфазные системы [7]. Переход из состояния микроэмульсии при этом носит обратимый характер: при охлаждении истинного раствора исходная микрогетерогенность восстанавливается. Существование устойчивой двухфазной области вызывало возражения Вертмана А.А. в связи с нарушением правила фаз в эвтектической точке [6]. Однако на несостоятельность этого утверждения указывал еще Френкель Я.И. [10]. В случае, если происходит диспергирование одной из фаз до коллоидного масштаба, появляется дополнительная степень свободы – давление внутри дисперсных частиц или их радиус [11].
Гипотеза о коллоидной микронеоднородности (микрогетерогенности) расплавов Fe – C была сформулирована на основании данных седиментационного эксперимента Вертманом А.А. и Самариным А.М. Проведенные ими совместно с и Якобсоном А.М. опыты по центрифугированию жидкого чугуна показали, что радиус группировок атомов углерода близок к 10 нм [12]. В работах Вертмана А.А. и Самарина А.М. коллоидная микронеоднородность (микрогетерогенность) расплава связывается с присутствием неравновесной дисперсной фазы, постепенно растворяющейся в дисперсионной среде [6]. Такая динамическая (флуктуационная) микронеоднородность обладает наследственной структурой ближнего порядка твердых эвтектических фаз, ее время жизни соизмеримо со временем релаксации в расположении атомов. Исследование микронеоднородного (коллоидного) состояния жидких чугунов привело Вертмана А.А. и Самарина А.М. к выводу о неравновесности такого состояния, что объясняло ветвление температурных зависимостей их физических свойств, полученных в режимах нагрева и последующего охлаждения расплава [13]. Залкиным В.М. предполагается ограниченная растворимость углерода в жидком железе, не превышающая 6,5 – 8,5 ат. % [7]. При более высокой концентрации углерода в расплаве самопроизвольно образуются обогащенные углеродом упорядоченные группировки разносортных атомов, близкие по строению к цементиту и являющиеся отдельными фазами. Образование дисперсных частиц цементита в жидких сплавах в этом интервале температур происходит при плавлении сплавов как с цементитом, так и с графитом в исходной структуре, а также при растворении графита в жидком железе. Увеличение содержания углерода в расплаве до более, чем 12,4 – 14,2 ат. %, приводит к появлению субмикрогруппировок атомов углерода, упорядоченных по типу графита [14]. В дальнейшем представления о микрогетерогенном состоянии расплавов Fe – C развивались как о временном, неравновесном состоянии, постепенно переходящем в равновесное состояние истинного раствора [15]. Представления о микрогетерогенности расплавов Fe – C позволяют провести анализ причин расхождения температурных зависимостей их кинематической вязкости и удельного электросопротивления на основе представлений теории явлений переноса в неоднородной среде. Как показали эксперименты, размер микрообластей, обогащенных одноименными атомами, достигает десятков нанометров, что существенно превышает масштаб ближнего упорядочения в расплавах и позволяет применять к расчету свойств мирогетерогенных расплавов известные зависимости теории явлений переноса в неоднородной среде [16]. Авторами ранее использован данный подход для определения температур перехода расплавов Fe – Mn – C от модели изолированных включений к модели взаимопроникающих включений [17], а также температур перехода от гетерогенной системы к однородному раствору [18].
На основе представлений о микрогетерогенном строении расплавов возможно применение теории о вязкости суспензий для анализа температурных зависимостей кинематической вязкости. Вязкость среды, содержащей дисперсные включения, превышает вязкость чистой жидкости вследствие появления напряжений при движении частиц. В этом случае говорят об эффективной вязкости среды. В случае разбавленных дисперсных систем можно считать, что сила межфазного взаимодействия при медленных режимах обтекания представляет собой силу Стокса, умноженную на число частиц в заданном объеме. Такой подход и использовался Эйнштейном [19; 20] для определения вязкости разбавленных дисперсных систем, содержащих твердые частицы, а так же Тейлором [19] для дисперсии из капель и пузырьков. В другом предельном случае, когда концентрация частиц настолько велика, что реализуется режим плотной упаковки, используют методы теории фильтрования, в основе которых лежит закон Дарси [21; 22].
Применительно к жидким металлам теория Эйнштейна была впервые использована для анализа явления послеплавления [23]. Уравнение Эйнштейна неоднократно использовалось при обсуждении вискозиметрического эксперимента с расплавами металлургического производства. Автор работы [24] отмечает, что повышение вязкости при охлаждении можно отнести на счет укрупнения единиц вязкого течения и кристаллизации. Вязкость суспензии определяется размером частиц дисперсии фазы и ее количеством в расплаве. Применительно к жидким сталям и чугунам было обнаружено, что наличие включений в расплаве оказывает существенное влияние на его вязкость [25] и сопротивление [26].
Сплавы с высоким содержанием углерода (до 4 %) и хрома (до 30 %) характеризуются повышенными прочностными характеристиками, в то же время детали из этих сплавов обладают большим сопротивлением износу и окислению, поэтому их относят к классу износостойких чугунов. Высокие характеристики этих сплавов обусловлены наличием большого количества карбидов хрома, которые обладают высокой твердостью. Именно размер, тип и морфология этих карбидов определяют износостойкость и ударную вязкость. Необходимые микроструктурные характеристики износостойких чугунов достигаются путем изменения химического состава, скорости кристаллизации или специальной термической обработкой [27].
В результате исследования влияния ванадия и хрома на микроструктуры белых чугунов, легированных Cr, V, Mn и Ni, выявлено, что ванадий и хром увеличивают общую карбидную долю и количество аустенита в матрице, карбиды ванадия (VC) являются центрами зарождения карбидной эвтектики [28]. Исследование влияния температуры обработки сплава привело авторов работы [29] к выводу, что повышение температуры до 850 °С способствует образованию в микроструктуре вторичных карбидов и мартенсита, что, в свою очередь, и обеспечивает высокие значения твердости. Авторами работы [30] показана рациональность использования термовременной обработки стали и чугуна в жидком состоянии при производстве ответственных отливок с высокой абразивной и ударно-абразивной износостойкостью. В частности, для стали 4Х5В2ФСЛ высокотемпературная обработка расплава способствует повышению прочностных свойств на 36 % с одновременным высоким значением износостойкости. Однако для чугуна ИЧХ28Н2 наибольшей абразивной и ударно-абразивной износостойкостью обладает сплав, выдержанный при температуре 1420 °С. Выдержка при температуре 1520 °С приводит к уменьшению микротвердости основы и эвтектики и повышению микротвердости на 400 HV отдельных карбидов хрома.
Предложен рациональный режим получения чугуна ИЧХ28Н2: нагрев расплава до температуры 1470 °С, выдержка в течение 15 мин, охлаждение расплава до температуры заливки, ввод (Ca, Sr)CO3 , а затем лигатуры БФТ-1 в количествах 3 и 4 кг/т соответственно. Применение разработанного метода обработки расплава чугуна оказывает также положительное влияние на жидкотекучесть – основное литейное свойство. Изучено влияние бора на условия кристаллизации жаростойких и износостойких чугунов Fe – C – Cr – Mn – Ni – Ti – Al – Nb [31].
Обнаружено увеличение твердости матрицы высокохромистых чугунов после термической обработки в результате совмещения выделения вторичных карбидов Me23C6 при дестабилизации и аустенитно-мартенситного превращения при закалке. Кинетические расчеты процесса дестабилизации показали, что при нагреве первыми выделяются вторичные карбиды Мe7С3 , достигающие максимума при 850 °С. При последующих нагреве до 980 °С и выдержке при этой температуре они полностью превращаются в Me23C6 [32]. При повышении температуры дестабилизации до 1000 °С увеличиваются количество, объем и размер вторичных карбидов (до 2,22 мкм). При 1050 °С и времени выдержки 3 ч размер вторичных карбидов значительно уменьшается с высокой плотностью распределения в матричной фазе, при этом образцы характеризуются лучшей коррозионной стойкостью [33]. Содержание углерода в матрице в зависимости от температуры дестабилизации и последующего растворения эвтектического карбида контролирует температуру начала образования мартенсита и оказывает доминирующее влияние на объемную твердость [34].
В работе [35] приведены данные о фазовом составе и структурообразовании сплавов и оксидных слоев, о распределении элементов по структурным компонентам сплава и поверхности окисления по глубине оксидного и подоксидного слоев, об изменении износостойкости, окалиностойкости, повышении стабильности и механических свойств чугуна системы Cr – Mn – Ni – Ti – Al – Nb в зависимости от различного содержания алюминия и ниобия и теплоаккумулирующей способности литейной формы.
Перегрев жидкого чугуна выше температуры 1500 °С приводит к уменьшению размеров первичных карбидов, при этом в интервале температур между линиями ликвидуса и солидуса обнаружена рекристаллизация первичных карбидов (Cr, Fe)7C3 , что приводит к значительному уменьшению содержания хрома и увеличению содержания в них железа [36]. Обнаружено изменение структуры и свойств заэвтектических хромистых чугунов после температурной обработки, которое, как полагают авторы работы [36], связано с существованием композиционно стабильных кластеров в расплаве в интервале от температуры плавления до ≈1500 °С. Это связано с высоким сродством хрома и углерода и наличием тугоплавкого карбида Cr7C3 . Обнаружено, что термообработка расплава в области температур 1260 – 1320 °С (между линиями ликвидус и солидус) приводит к повышению износостойкости, повышение же температуры обработки приводит к снижению износостойкости слитков. Термообработка мелкокристаллических отливок из заэвтектического хромистого железа в диапазоне температур между ликвидусом и солидусом вызывает перекристаллизацию первичных кристаллов карбида (Cr, Fe)7C3 с изменением их состава, формы и незначительным увеличением размера. В этом случае доля первичных карбидов увеличивается, а доля эвтектических карбидов уменьшается с понижением температуры термобработки.
Микроструктура слитков Fe – Cr – C включает первичные и вторичные дендриты твердого раствора Fe – Cr, декорированные сложными карбидами Me23C6 и Me7C3 [37]. Микроструктура сплава Fe – 34Cr – 4,5C представляет собой обогащенную хромом аустенитную матрицу с карбидами Me7C3 , которая сохранятся до температур чуть выше 1150 °С и имеет метастабильный характер [38]. Исходя из этого предполагается, что в жидком состоянии расплав Fe – Cr – C в контексте микрогетерогенного строения можно понимать как дисперсные частицы Fe – Cr, распределенные в дисперсионной среде Fe – C.
Таким образом, жидкий чугун можно рассматривать как коллоидную систему, состоящую из дисперсионной среды и включений. В этом случае к таким системам применимы представления теории явлений переноса в неоднородных средах, а также представления теории о вязкости суспензий. В данной работе поставлена цель из анализа экспериментальных данных о кинематической вязкости и удельном электросопротивлении определить объемную долю дисперсных частиц в расплавах чугунов ИЧХ28Н2 и ИЧ310Х24М2Ф4ТР. Для определения объемной доли дисперсных частиц предполагается использовать известные представления теории вязкого течения суспензий и теории явлений переноса в неоднородных средах.
Методы исследования
Экспериментальные методы исследования
В качестве объектов исследования были отобраны образцы промышленных сплавов износостойкого чугуна ИЧХ28Н2, легированного Cr и Ni, а также ИЧ310Х24М2Ф4ТР, легированного Cr, Mo, V и Ti, полученные в лабораторных условиях с соблюдением технологии выплавки износостойких чугунов. Химический состав образцов определен с помощью спектрометра с искровым источником возбуждения спектра (SPECTROMAXx, SPECTRO Analytical Instruments GmbH, Германия) и приведен в таблице. В лабораторных условиях исследовано удельное электросопротивление и кинематическая вязкость данных образцов.
Удельное электросопротивление ρ сплавов износостойких чугунов в жидком состоянии измеряли методом Регеля по углу закручивания контейнера с исследуемым образцом под действием вращающего магнитного поля при отношении высоты образца к диаметру h/d ≈ 1. Регель А.Р. показал, что угол закручивания подвесной системы φ пропорционален удельной проводимости металла, если радиус цилиндрического образца соизмерим с высотой [39 – 41]. Измерения удельного электросопротивления проводили на оригинальной установке, описанной в работе [42].
Кинематическую вязкость ν износостойких чугунов в жидком состоянии измеряли методом крутильных колебаний тигля с расплавом в одном торцевом варианте [43; 44]. Кинематическую вязкость определяли по затухающим крутильным колебаниям тигля с расплавом путем регистрации периода колебаний и логарифмического декремента затухания, затем расчетным путем определяли величину кинематической вязкости исследуемого расплава. При этом высота жидкого сплава должна составлять 2H ≥ 1,85R относительно радиуса тигля с расплавом для обеспечения полного затухания вязких волн, распространяющихся от дна тигля к свободной поверхности.
Измерение удельного электросопротивления и кинематической вязкости проведены в интервале температур от TL до 1650 °C. Рабочую камеру предварительно вакуумировали до 0,001 Па. Затем запускали гелий до давления ~105 Па. Образцы выдерживали в камере с инертной средой в течение 10 – 15 мин при температуре TL , затем производили нагрев до 1650 °C с шагом 30 – 40 °C. Систематическая погрешность измерения ρ и ν составляла 3 %, а случайная погрешность, определяющая разброс точек в ходе одного опыта, при доверительной вероятности p = 0,95 не превышала 1,5 %.
Температуру ликвидус определяли по данным вискозиметрического исследования по резкому изменению логарифмического декремента затухающих крутильных колебаний тигля с расплавом по методике, описанной в работе [45].
Расчет объемной доли микрогетерогенных включений
Для определения объемной доли включений в жидких чугунах применялся подход на основании теории проводимости неоднородных сред и теоретических представлений о вязкости суспензий. Для этого жидкий чугун понимался как микрогетерогенная система, в которой дисперсные частицы распределены в дисперсионной среде. Для сплавов ИЧХ28Н2 и ИЧ310Х24М2Ф4ТР в жидком состоянии в качестве дисперсионной среды предполагается расплав Fe – 3 % С, а дисперсными частицами является расплав Fe – 30 % Cr.
При анализе результатов вискозиметрического эксперимента жидких чугунов для оценки объемной доли дисперсной фазы φ в расплавах применяли уравнение Тейлора [19], полученное для дисперсии, состоящей из капелек и пузырьков:
| \[{\eta _\varphi } = {\eta _2}\left[ {1 + 2,5\varphi \left( {\frac{{{\eta _1} + 0,4{\eta _2}}}{{{\eta _1} + {\eta _2}}}} \right)} \right],\] | (1) |
где ηφ – эффективная вязкость дисперсии; η1 и η2 – вязкость дисперсной и сплошной фаз соответственно.
По полученным экспериментальным данным о температурной зависимости кинематической вязкости ν определяли динамическую вязкость η жидкого чугуна из выражения η = νd. Плотность d жидкого чугуна определялась из аддитивной зависимости от содержания компонента в расплаве Xl и его температурной зависимости плотности dl .
В жидком состоянии расплав понимался как микрогетерогенная система, состоящая из дисперсных частиц Fe – 30 % Cr и дисперсионной среды Fe – 3 % C. Динамическую вязкость такой системы можно оценить по уравнению Тейлора (1)
| \[{\eta _{ef}} = {\eta _{{\rm{Fe}} - {\rm{C}}}}\left[ {1 + 2,5\varphi \left( {\frac{{{\eta _{{\rm{Fe}} - {\rm{Cr}}}} + 0,4{\eta _{{\rm{Fe}} - {\rm{C}}}}}}{{{\eta _{{\rm{Fe}} - {\rm{C}}}} + {\eta _{{\rm{Fe}} - {\rm{Cr}}}}}}} \right)} \right],\] | (2) |
где ηef – вязкость жидкого чугуна; ηFe – C – вязкость расплава Fe – C; ηFe – Cr – вязкость расплава Fe – Cr.
Экспериментальные данные о вязкости расплавов Fe – C с содержанием С до 5 % были получены в работе [46] и смоделированы методами молекулярной динамики в работе [47]. Вязкость расплавов системы Fe – Cr до 40 ат. % и Fe85 – xCr15Cx (x = 10 – 17 ат. %) была изучена авторами в работах [48; 49]. Известные экспериментальные данные о температурных зависимостях вязкости расплавов Fe – C, Fe – Cr и жидких чугунов аппроксимировались экспоненциальным выражением вида
| \[\eta = A\exp \left( {\frac{b}{T}} \right).\] | (3) |
Для определения объемной доли дисперсных частиц Fe – C в жидком чугуне было составлено уравнение
| \[{\eta _{ef}} - {\eta _{{\rm{Fe}} - {\rm{C}}}}\left[ {1 + 2,5\varphi \left( {\frac{{{\eta _{{\rm{Fe}} - {\rm{Cr}}}} + 0,4{\eta _{{\rm{Fe}} - {\rm{C}}}}}}{{{\eta _{{\rm{Fe}} - {\rm{C}}}} + {\eta _{{\rm{Fe}} - {\rm{Cr}}}}}}} \right)} \right] = 0.\] | (4) |
При анализе результатов резистометрического эксперимента с расплавами чугунов для оценки объемной доли дисперсной фазы φ в расплавах применяли уравнение Оделевского [50], связывающее электропроводность двухфазной системы σ с электропроводностями растворителя σs и дисперсных частиц σp :
| \[\begin{array}{c}\sigma = \frac{{2{\sigma _s} - {\sigma _p} + \varphi (3{\sigma _p} + {\sigma _s})}}{4} + \\ + \sqrt {{{\left( {\frac{{2{\sigma _s} - {\sigma _p} + \varphi (3{\sigma _p} + {\sigma _s})}}{4}} \right)}^2} + \frac{{{\sigma _s}{\sigma _p}}}{2}} .\end{array}\] | (5) |
Экспериментальные данные об удельном электросопротивлении расплавов Fе – С с содержанием до 4,2 % С были получены авторами работы [51]. Экспериментальные данные о сопротивлении расплавов Fe – Cr в широком диапазоне составов исследованы в работе [52]. Известные экспериментальные данные о температурной зависимости удельного электросопротивления расплавов аппроксимировались линейными зависимостями.
Для определения объемной доли дисперсных частиц Fe – C в жидком чугуне было составлено уравнение
| \[\begin{array}{c}{\sigma _{ef}} - \frac{{2{\sigma _s} - {\sigma _p} + \varphi (3{\sigma _p} + {\sigma _s})}}{4} + \\ + \sqrt {{{\left( {\frac{{2{\sigma _s} - {\sigma _p} + \varphi (3{\sigma _p} + {\sigma _s})}}{4}} \right)}^2} + \frac{{{\sigma _s}{\sigma _p}}}{2}} = 0,\end{array}\] | (6) |
где \({\sigma _{ef}} = \frac{1}{{{\rho _{ef}}}}\) – проводимость жидкого чугуна; \({\sigma _s} = \frac{1}{{{\rho _{{\rm{Fe}} - {\rm{C}}}}}}\) – проводимость расплава Fe – C; \({\sigma _p} = \frac{1}{{{\rho _{{\rm{Fe}} - {\rm{Cr}}}}}}\) – проводимость расплава Fe – Cr.
Уравнения (4) и (6) при известных данных о свойствах двойных систем Fe – C (ηFe – C , σs ), Fe – Cr (ηFe – Cr , σp ) и жидкого чугуна (ηef , σef ) решались относительно объемной доли включений (φ) методом fsolve библиотеки SciPy в интервале температур 1310 – 1650 °С.
Мольную долю дисперсных частиц определяли, исходя из полученных данных об объемной доле включений по выражению
| \[{m_i} = \frac{{{n_i}}}{{{n_\Sigma }}},{\rm{ }}{n_i} = \frac{{{\varphi _i}}}{{{M_i}}}{d_i},\] | (7) |
где mi , ni , φi , Mi , di – мольная доля, число молей на единицу объема, объемная доля, молярная масса и плотность i-го компонента соответственно.
Результаты работы и их обсуждение
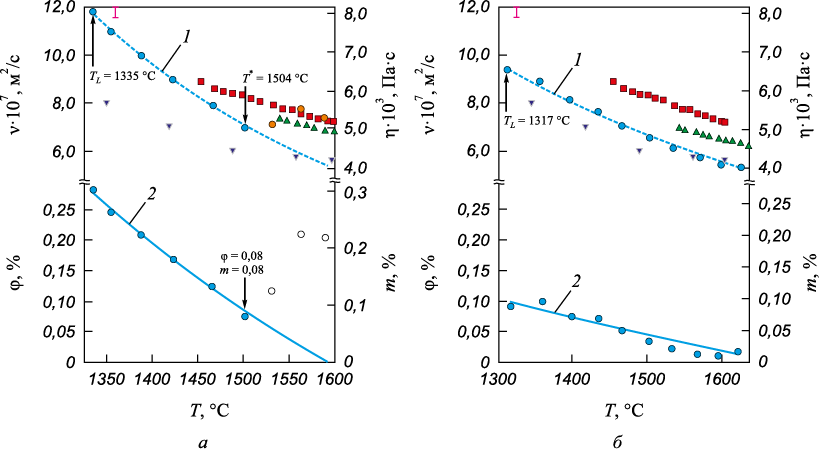
Результаты экспериментального исследования кинематической вязкости в интервале температур от TL до 1650 °C для жидких чугунов ИЧХ28Н2 и ИЧ310Х24М2Ф4ТР представлены на рис. 1. Полученные в данной работе значения кинематической вязкости согласуются с данными о вязкости расплава Fe – 15 ат. % Cr – 10 ат. % С авторов работы [48]. На правой оси того же графика (рис. 1) представлены значения динамической вязкости. Под температурной зависимостью кинематической вязкости приведены экспериментальные и расчетные данные об объемной (правая ось графика) и мольной (левая ось графика) долях гетерогенных включений в жидких чугунах. По результатам вискозиметрического исследования определены температуры ликвидус для жидких чугунов по методике, описанной в работе [45]. Температуры ликвидус нанесены на температурные зависимости кинематической вязкости.
Рис. 1. Температурные зависимости кинематической вязкости (ν), динамической вязкости (η), объемной (φ) и мольной доли (m) гетерогенных включений в жидких чугунах ИЧХ28Н2 (а) |
При анализе результатов вискозиметрического эксперимента с жидкими чугунами для оценки объемной доли дисперсной фазы φ в расплавах применяли подход, предложенный Эйнштейном А. для описания вязкости дисперсных систем [19; 20]. Им рассмотрен случай стесненного обтекания системы сферических частиц потоком жидкости и вводит понятие эффективной вязкости среды. Скорость движения частиц в стесненном потоке зависит не только от их размера, формы, физико-химических свойств среды, но и от объемной концентрации φ. Зависимость от объемной концентрации обусловлена гидродинамическим взаимодействием между частицами. Скорость частицы в стесненном потоке, как правило, меньше скорости изолированной частицы. Вязкость среды, содержащей дисперсные включения, превышает вязкость чистой жидкости вследствие появления напряжений при движении частиц. В этом случае говорят об эффективной вязкости среды. Строгого описания закономерностей стесненного движения частиц в вязком потоке до сих пор не существует. Для случая разбавленных дисперсных систем такой подход использовался Эйнштейном [19] для определения эффективной вязкости среды, содержащей твердые частицы, а так же Тейлором [19] для определения дисперсии из капель и пузырьков. Расплав, как микрогетерогенная система, понимался как дисперсные частицы, обогащенные Cr (Fe – 30 % Cr), распределенные в дисперсионной среде Fe – 3 % C. По известным значениям вязкости расплавов Fe – Cr и Fe – C [46 – 48] и полученным экспериментальным данным о вязкости дисперсной системы из решения уравнения (4) получены значения объемной доли дисперсных частиц (Fe – 30 % Cr) в жидких чугунах. Расчетные значения объемной доли включений (рис. 1) получены из аппроксимированных уравнением (3) температурных зависимостей кинематической вязкости расплавов Fe – 3 % C, Fe – 30 % Cr и жидких чугунов. Значения объемной доли дисперсных частиц, отмеченные символом ![]() на рис. 1, получены из экспериментальных значений о кинематической вязкости жидких чугунов и аппроксимированных уравнением (3) значений кинематической вязкости дисперсных частиц (Fe – 30 % Cr) и дисперсионной среды (Fe – 3 % C). Мольную долю дисперсных частиц определяли по полученным данным об объемной доле из уравнения (7).
на рис. 1, получены из экспериментальных значений о кинематической вязкости жидких чугунов и аппроксимированных уравнением (3) значений кинематической вязкости дисперсных частиц (Fe – 30 % Cr) и дисперсионной среды (Fe – 3 % C). Мольную долю дисперсных частиц определяли по полученным данным об объемной доле из уравнения (7).
Зависимость кинематической вязкости от температуры для жидкого чугуна ИЧХ28Н2 в интервале от TL до 1504 °C подчиняется экспоненциальному закону и согласуется с уравнением Аррениуса. В этом же интервале температур объемная и мольная доли снижаются с 0,28 (0,30) до 0,08 (0,08). Однако при температуре выше 1504 °C обнаружено аномальное возрастание кинематической вязкости с повышением температуры (отмеченно символом ![]() на рис. 1, а), которое сопровождается также аномальным повышением объемной доли дисперсных частиц в жидком чугуне, отклоняющееся от расчетной кривой. Такое поведение может быть связано со структурными изменениями в расплаве. При растворении дисперсных частиц расплав переходит в состояние более однородного раствора, при этом изменяется химический состав дисперсной фазы, что и приводит к аномальному увеличению вязкости. В этом случае уравнение (4) неприменимо для описания вязкого течения однородной системы.
на рис. 1, а), которое сопровождается также аномальным повышением объемной доли дисперсных частиц в жидком чугуне, отклоняющееся от расчетной кривой. Такое поведение может быть связано со структурными изменениями в расплаве. При растворении дисперсных частиц расплав переходит в состояние более однородного раствора, при этом изменяется химический состав дисперсной фазы, что и приводит к аномальному увеличению вязкости. В этом случае уравнение (4) неприменимо для описания вязкого течения однородной системы.
Кинематическая вязкость для жидкого чугуна ИЧ310Х24М2Ф4ТР монотонно снижается при повышении температуры, также монотонно снижается и объемная (мольная) доля гетерогенных включений в жидком чугуне с 0,10 (0,10) при температуре ликвидус до 0,01 (0,01). Это свидетельствует о растворении гетерогенных включений в расплаве с повышением температуры.
По данным вискозиметрического эксперимента проведена оценка размера структурной единицы вязкого течения расплавов чугунов ИЧХ28Н2 и ИЧ310Х24М2Ф4ТР. Использован метод, предложенный в работе [53] для определения размера структурной единицы вязкого течения. Температурная зависимость кинематической вязкости представлена в виде
| \[\nu = \frac{{B{T^{1/2}}}}{{{s^{1/2}}}}\exp \left( {\frac{\varepsilon }{{kT}}} \right),\] | (8) |
где \(B = \frac{\pi }{4}{\left( {\frac{k}{{3d}}} \right)^{1/2}};\) s – размер дисперсных частиц.
Получено, что для расплава ИЧХ28Н2 s = 1,3 нм, для расплава ИЧ310Х24М2Ф4ТР s = 1,4 нм, что по порядку величины согласуется с данными работы [54], полученными для жидкой стали 110Г13Л.
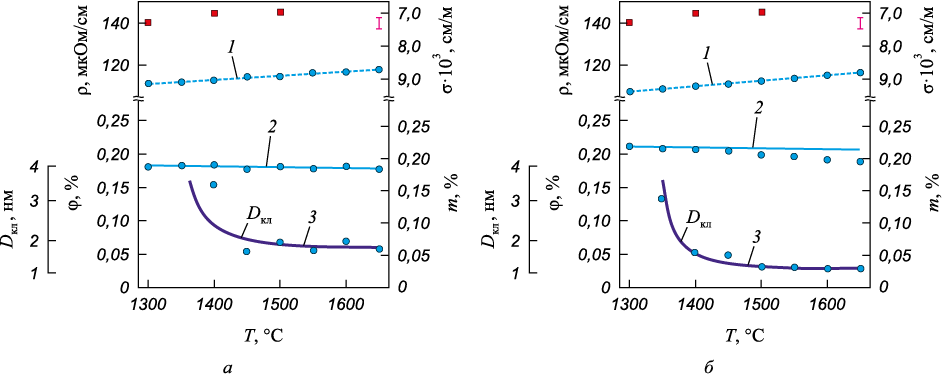
Результаты резистометрического исследования жидких чугунов ИЧХ28Н2 и ИЧ310Х24М2Ф4ТР представлены на рис. 2. Значения удельного электросопротивления показаны на левой оси графика, на правой оси – значения удельной проводимости жидких чугунов. Ниже под экспериментальными данными об удельном электросопротивлении (проводимости) представлены полученные значения объемной (левая ось) и мольной (правая ось) доли дисперсных частиц для жидких чугунов.
Рис. 2. Температурные зависимости удельного электросопротивления (ρ), |
Анализ результатов измерения удельного электросопротивления производился на основании представлений теории проводимости неоднородных сред. Жидкий чугун понимался как дисперсные частицы, обогащенные Cr (Fe – 30 % Cr), распределенные в дисперсионной среде Fe – 3 % C. В рамках представлений о проводимости неоднородных средств определена объемная доля дисперсных частиц в жидких чугунах из решения уравнения (6) по известным данным о проводимости (1/ρ) дисперсных частиц (Fe – 30 % Cr) [52], дисперсионной среды (Fe – 3 % C) [51] и экспериментальным данным о проводимости жидкого чугуна. Расчетные значения объемной доли (рис. 2) получены из аппроксимированных прямолинейной зависимостью известных экспериментальных данных о температурных зависимостях проводимости Fe – 3 % C, Fe – 30 % Cr и жидких чугунов. Значения объемной доли дисперсных частиц на рис. 2 получены из экспериментальных данных о проводимости жидких чугунов и аппроксимированных прямолинейной зависимостью значений проводимости дисперсных частиц (Fe – 30 % Cr) [52] и дисперсионной среды (Fe – 3 % C) [51]. Вблизи температуры плавления объемная (мольная) доля дисперсных частиц составляет 0,18 (0,19) для ИЧХ28Н2 и 0,21 (0,22) для ИЧ310Х24М2Ф4ТР. С повышением температуры объемная (мольная) дисперсных частиц снижается незначительно.
В работе [55] для микронеоднородных металлических расплавов предложено следующее выражение:
| \[\ln \left( {\frac{\rho }{{{\rho _L}}}} \right) = \frac{{{l_{\rm{ж}}}}}{{{D_{{\rm{кл}}}}}}\ln \left( {\frac{1}{r}} \right),\] | (9) |
где ρL , ρ – удельное электросопротивление жидкого железа при температуре ликвидус и температуре анализа соответственно; lж – длина свободного пробега электронов жидкого железа; Dкл – диаметр кластера; r – коэффициент рассеяния электронов проводимости.
Длина свободного пробега электронов в жидком железе уменьшается от 4,63 до 4,28 Å при нагреве расплава от 1400 до 1600 °С. Поскольку коэффициент рассеяния изменяется в пределах 0 < r < 1, то из выражения (4) следует, что с уменьшением размера кластеров электросопротивление расплава должно расти. Выполненные расчеты показали, что при t = 1600 °С величина r = 0,97, а при t = 1800 °С r = 0,86, т. е. при нагреве r уменьшается, а ρ растет. Определенный по уравнению (8) размер кластера (рис. 2) для ИЧХ28Н2 при температуре 1400 °С составляет 3,4 нм и при температуре выше 1600 °С уменьшается до 1,7 нм, а для ИЧ310Х24М2Ф4ТР при температуре 1400 °С составляет 1,7 нм и при температуре выше 1600 °С уменьшается до 1,2 нм. Следовательно, наблюдаемый экспериментально рост электросопротивления жидкого железа при повышении температуры, по-видимому, не связан с изменениями структуры расплава на атомном уровне, а определяется уменьшением количества электронов проводимости. Последнее объясняется увеличением числа электронов, участвующих в укреплении межатомных связей, и обеспечением устойчивости кластеров при их измельчении с ростом температуры.
В итоге, по результатам вискозиметрического и резистометрического исследования установлено, что жидкие чугуны представляют собой дисперсную систему, содержащую вблизи температуры плавления объемную долю дисперсных частиц от 0,28 и 0,10 по данным вискозиметрии для жидких чугунов ИЧХ28Н2 и ИЧ310Х24М2Ф4ТР соответственно, что соответствует размерам дисперсных частиц от 100 до 10 нм. По данным резистометрии объемная доля дисперсных частиц составляет около 0,20 для жидких чугунов и с повышением температуры существенно не изменяется. Объемной доли 0,20 отвечают дисперсные частицы, имеющие размер около 10 нм. Согласно оценок авторов работы [56], сделанных в рамках квазихимической модели микронеоднородного строения сложнолегированных расплавов [1], мольная доля кластеров в жидких чугунах ИЧХ28Н2 и ИЧ310Х24М2Ф4ТР составляет 0.43 при температуре ликвидус, что значительно выше значений, полученных в данной работе. Исходя из этого можно рассматривать жидкий чугун в качестве микрогетерогенной системы. Повышение температуры приводит к снижению объемной доли дисперсных частиц, что соответствует представлению о разрушении микрогетерогенного состояния с перегревом жидкого расплава выше некоторой температуры.
Выводы
В работе приведены экспериментальные данные температурных зависимостей кинематической вязкости и удельного электросопротивления жидких чугунов в интервале от температуры ликвидус TL до 1650 °C. Жидкий чугун рассматривался как микрогетерогенная система, характеризующаяся наличием дисперсных частиц, обогащенных одним из компонентов.
По данным о кинематической вязкости жидких чугунов определена объемная доля гетерогенных включений в рамках представлений вязкого течения разбавленных дисперсных систем. Обнаружено, что объемная доля дисперсных частиц в жидких чугунах вблизи температуры плавления составляет 0,28 для ИЧХ28Н2 и 0,1 для ИЧ310Х24М2Ф4ТР. Объемная доля 0,28 соответствует размеру дисперсных частиц ~100 нм, а 0,1 соответствует размеру ~10 нм. Полученный размер дисперсных частиц согласуется с представлениями о микрогетерогенном строении жидких чугунов. С повышением температуры объемная доля дисперсных частиц монотонно снижается до значений 0,08 – 0,01.
Также объемная доля дисперсных частиц определена по данным об удельном электросопротивлении жидких чугунов, которая составила 0,18 для ИЧХ28Н2 и 0,21 для ИЧ310Х24М2Ф4ТР. Полученные значения объемной доли соответствуют размеру дисперсных частиц ~10 нм. С увеличением температуры объемная доля дисперсных частиц снижается незначительно.
Известно, что температурная обработка расплава с целью разрушения микрогетерогенного строения приводит к модифицированию структуры закристаллизованного слитка за счет изменения условий кристаллизации. Однако авторами работ [30; 36] обнаружено, что перегрев расплавов хромистых чугунов приводит к понижению износостойкости слитков. В работе [36] отмечено, что перегрев расплава выше 1500 °C приводит к разрушению композиционно стабильных кластеров в расплаве, что приводит к изменению структуры и свойств заэвтектических хромистых чугунов после температурной обработки. С целью повышения эксплуатационных свойств в работе [30] предлагается введение дополнительных модификаторов перед выпуском чугуна после термо-временной обработки расплава, а в работе [36] показано, что повысить износостойкость можно температурной обработкой между температурами ликвидус и солидус. Таким образом, исследование расплавов хромистых чугунов в жидком состоянии с точки зрения их микронеоднородного строения позволит приблизится к пониманию процессов, протекающих в жидком состоянии, и выработать оптимальный режим термообработки расплава с целью повышения его эксплуатационных характеристик.
Список литературы
1. Чикова О.А. О структурных переходах в сложнолегированных расплавах. Известия вузов. Черная металлургия. 2020;63(3–4):261–270. https://doi.org/10.17073/0368-0797-2020-3-4-261-270
2. Сидоров В.Е., Сон Л.Д. Исследование расплавов как основа совершенствования технологий черной металлургии. Черные металлы. 2023;(3):58–64. https://doi.org/10.17580/chm.2023.03.10
3. Тягунов Г.В., Барышев Е.Е., Тягунов А.Г., Мушников В.С., Костина Т.К. О некоторых особенностях структурирования металлических жидкостей. Вестник Южно-Уральского государственного университета. Серия: Металлургия. 2018;18(3):16–25. https://doi.org/10.14529/met180302
4. Попель П.С. Метастабильная микрогетерогенность расплавов в системах с эвтектикой и монотектикой и ее влияние на структуру сплава после затвердевания. Расплавы. 2005;(1):22–48.
5. Клячко Ю.А. Опыт коллоидно-химического исследования металлов. Москва: Издательство Академии им. К.Е. Ворошилова; 1935:92.
6. Вертман А.А. Микрогетерогенность металлических расплавов и проблема регулирования свойств отливок. Физика и химия обработки материалов. 1967;(3):132–141.
7. Залкин В.М. Природа эвтектических сплавов и эффект контактного плавления. Москва: Металлургия; 1987:152.
8. Залкин В.М. О двух теориях начальной стадии контактного плавления. Расплавы. 2004;(2):93–95.
9. Залкин В.М. О микрогетерогенном строении эвтектических сплавов (растворов) в жидком состоянии. Журнал физической химии. 2005; 79(4):763–765.
10. Френкель Я.И. Статистическая физика. Москва: Издательство АН СССР; 1948:760.
11. Морохов Д.И., Трусов Л.И., Лаповок В.Н. Физические явления в ультрадисперсных средах. Москва: Энергоатомиздат; 1984:224.
12. Вертман А.А., Самарин А.М., Якобсон А.М. О строении жидких эвтектик. Известия АН СССР. ОТН. Металлургия и топливо. 1960;(3):17–21.
13. Вертман А.А., Самарин А.М., Туровский Б.М. Строение жидких сплавов системы железо-углерод. Известия АН СССР. ОТН. Металлургия и топливо. 1960;(6):123–129.
14. Вертман А.А., Самарин А.М. Свойства расплавов железа. Москва: Наука; 1969:197.
15. Бродова И.Г., Замятин В.М., Попель П.С., Есин В.О., Баум Б.А., Моисеев А.И., Коршунов И.П., Топчий А.Л., Тихомиров Ю.Г., Поленц И.В. Условия формирования метастабильных фаз при кристаллизации сплавов Al-Zr. Расплавы. 1988;(6–2):23–27.
16. Дульнев Г.Н., Новиков В.В. Процессы переноса в неоднородных средах. Ленинград: Энергоатомиздат; 1991:248.
17. Синицин Н.И., Чикова О.А., Вьюхин В.В. Удельное электросопротивление расплавов Fe–Mn–C. Неорганические материалы. 2021;57(1):89–97. https://doi.org/10.31857/S0002337X21010127
18. Чикова О.А., Синицин Н.И., Вьюхин В.В. Электросопротивление сплавов Fe-Mn в жидком состоянии. Известия вузов. Физика. 2021;64(6):68–75. https://doi.org/10.17223/00213411/64/6/68
19. Бибик Е.Е. Реология дисперсных систем. Ленинград: Издательство Ленинградского университета; 1981:172.
20. Хаппель Дж., Бреннер Г. Гидродинамика при малых числах Рейнольдса. Москва: Мир; 1976:630.
21. Урьев Н.П. Высококонцентрированнные дисперсные системы. Москва: Химия; 1980:149.
22. Реология: Теория и приложения. Пер. с англ. / Под ред. Ф. Эйриха; Под общ. ред. Ю.Н. Работнова и П.А. Ребиндера. Москва: Издательство иностранной литературы; 1962:824.
23. Глазов В.М., Тимошенко В.И. Анализ явления послеплавления в расплавах полупроводников на основе кластерной модели. Журнал физической химии. 1981;55(6): 1148–1452.
24. Морозов А.А. Технологические свойства и строение титанатных расплавов. Цветные металлы. 2002;(8):60–63.
25. Боровых М.А., Вьюхин В.В., Чикова О.А., Цепелев В.С. О влиянии дефектов на вязкость жидких сталей 32Г1 и 32Г2. Известия вузов. Черная металлургия. 2015;58(6): 402–406. https://doi.org/10.17073/0368-0797-2015-6-402-406
26. Боровых М.А., Чикова О.А., Цепелев В.С., Вьюхин В.В. О влиянии режима термообработки на удельное электросопротивление расплава стали 35ХГФ. Известия вузов. Черная металлургия. 2018;61(3):237–243. https://doi.org/10.17073/0368-0797-2018-3-237-243
27. Abdel-Aziz K., El-Shennawy M., Omar A. Microstructural characteristics and mechanical properties of heat treated high-Cr white cast iron alloys. International Journal of Applied Engineering Research. 2017;12(14):4675–4686.
28. Efremenko V.G., Shimizu K., Cheiliakh A.P., Kozarevskaya T.V., Kusumoto K., Yamamoto K. Effect of vanadium and chromium on the microstructural features of V-Cr-Mn-Ni spheroidal carbide cast irons. International Journal of Minerals Metallurgy and Materials. 2014;21(11):1096–1108. https://doi.org/10.1007/s12613-014-1014-6
29. Karantzalis A.E., Lekatou A., Kapoglou A., Mavros H., Dracopoulos V. Phase transformations and microstructural observations during subcritical heat treatments of a high-chromium cast iron. Journal of Materials Engineering and Performance. 2012;21(6):1030–1039. https://doi.org/10.1007/s11665-011-9995-z
30. Колокольцев В.М., Михалкина И.В., Шевченко А.В. Высокотемпературная обработка расплавов специальных сталей и чугунов. Литейщик России. 2016;(9):18–23.
31. Колокольцев В.М., Петроченко Е.В., Молочкова О.С. Влияние бора и температурных режимов охлаждения металла в литейной форме на структурно-фазовое состояние жароизносостойких белых чугунов. Известия вузов. Черная металлургия. 2019;62(11):887–893. https://doi.org/10.17073/0368-0797-2019-11-887-893
32. Guitar M.A., Nayak U.P., Britz D., Mücklich F. The effect of thermal processing and chemical composition on secondary carbide precipitation and hardness in high-chromium cast irons. International Journal of Metalcasting. 2020;14(3):755–765. https://doi.org/10.1007/s40962-020-00407-4
33. Quyen Hoang Thi Ngoc, Ngoc Tran Vu Diem, Viet Nguyen Hoang, Hai Nguyen Hong, Ha Le Thu, Nam Nguyen Duong. Effect of residual stress distribution on the formation, growth and coalescence of voids of 27Cr white cast iron under impact loading. Materials Transactions. 2022;63(2):170–175. https://doi.org/10.2320/matertrans.MT-M2021161
34. Le Nué C., Corujeira Gallo S., Vahid A., Wang J., Taherishargh M., Attar H., Fabijanic D., Barnett M. Destabilization treatment and its influence on microstructure and matrix hardness of high-Cr cast iron. Metallurgical and Materials Transactions A. 2023;54(12):4952–4965. https://doi.org/10.1007/s11661-023-07216-4
35. Kolokoltsev V.M., Petrochenko E.V., Molochkova O.S. Influence of aluminium and niobium alloying on phase composition, structure and properties of heat- and wear-resistant cast iron of Cr-Mn-Ni-Ti system. CIS Iron and Steel Review. 2021;(2):55–60. https://doi.org/10.17580/cisisr.2021.02.10
36. Panichkin A., Wieleba W., Kenzhegulov A., Uskenbayeva A., Mamaeva A., Imbarova A., Kvyatkovskii S., Kasenova B. Effect of thermal treatment of chromium iron melts on the structure and properties of castings. Materials Research Express. 2023;10(8):086502. https://doi.org/10.1088/2053-1591/acead7
37. Wieczerzak K.K., Bała P., Stępień M., Cios G., Kozieł T. The Characterization of Cast Fe-Cr-C Alloy. Archives of Metallurgy and Materials. 2015;60(2):779–782. https://doi.org/10.1515/amm-2015-0206
38. Svensson L.-E., Gretoft B., Ulander B., Bhadeshia H.K.D.H. Fe-Cr-C hardfacing alloys for high-temperature applications. Journal of Materials Sci. 1986;21(3):1015–1019. https://doi.org/10.1007/BF01117388
39. Цепелев В.С. Физика аморфных и нанокристалличеких металлических расплавов: методология анализа: Монография. Екатеринбург: Издательство Уральского университета; 2023:208.
40. Регель А.Р. Безэлектродный метод измерения электропроводности и возможности его применения для задач физико-химического анализа. Журнал неорганической химии. 1956;1(6):1271–1277.
41. Рябина А.В., Кононенко В.И., Ражабов А.А. Безэлектродный метод измерения электросопротивления металлов в твердом и жидком состояниях и установка для его реализации. Расплавы. 2009(1):36–42.
42. Тягунов Г.В., Баум Б.А., Цепелев В.С., Тягунов А.Г., Влох А.Н. Измерение удельного электрического сопротивления методом вращающегося магнитного поля. Заводская лаборатория. 2003;69(2):36–38.
43. Швидковский Е.Г. Некоторые вопросы вязкости расплавленных металлов. Москва: Гостехиздат; 1955:206.
44. Конашков В.В., Цепелев В.С., Вьюхин В.В., Поводатор А.М., Подольская А.И. Автоматизированная установка для изучения кинематической вязкости высокотемпературных металлических расплавов. Приборы и техника эксперимента. 2011;(2):149–150.
45. Чикова О.А., Шмакова К.Ю., Цепелев В.С. Определение температур фазовых равновесий высокоэнтропийных металлических сплавов вискозиметрическим методом. Металлы. 2016;(2):54–59.
46. Tanaka T., Hara S. Surface tension and viscosity of liquid iron alloys. Materia Japan. 1997;36(1):47–54.
47. Feng G., Jiao K., Zhang J., Gao S. High-temperature viscosity of iron-carbon melts based on liquid structure: The effect of carbon content and temperature. Journal of Molecular Liquids. 2021;330:115603. https://doi.org/10.1016/j.molliq.2021.115603
48. Kamaeva L.V., Sterkhova I.V., Lad’yanov V.I. Viscosity and supercooling of Fe-Cr (≤40 at % Cr) melts. Inorganic Materials. 2012;48(3):318–324. https://doi.org/10.1134/S0020168512030089
49. Sterkhova I.V., Kamaeva L.V., Lad`yanov V.I. Viscosity of the eutectic Fe85-xCr15Cx (x = 10–17) melts. Physics and Chemistry of Liquids. 2020;58(5):559–565. https://doi.org/10.1080/00319104.2019.1616194
50. Оделевский В.И. Расчет обобщенной проводимости гетерогенных систем. Журнал технической физики. 1951;21(6):667–685.
51. Ono Y., Hirayama K., Furukawa K. Electric resistivity of molten Fe-C, Fe-Si, and Fe-C-Si alloys. Tetsu-to-Hagane. 1974;60(14):2110–2118. https://doi.org/10.2355/tetsutohagane1955.60.14_2110
52. Кудрявцева Е.Д., Сингер В.В., Радовский И.З. Электронная структура жидких сплавов железа с марганцем, хромом и ванадием. Известия вузов. Физика. 1983;(1):55–58.
53. Чикова О.А., Цепелев В.С., Московских О.П. Оценка параметров микрогетерогенной структуры металлических расплавов из результатов вискозиметрического эксперимента на основе представлений теории абсолютных скоростей реакций. Журнал физической химии. 2017;91(6):925–930.
54. Чикова О.А., Синицин Н.И., Вьюхин В.В. Параметры микрогетерогенной структуры жидкой стали 110Г13Л. Журнал физической химии. 2019;93(8):1138–1146. https://doi.org/10.1134/S0044453719080065
55. Тягунов Г.В., Барышев Е.Е., Вандышева И.В., Зайцева Н.В., Хоменко А.О. Структура и свойства жидкого железа. Вестник ЮУрГУ. Серия “Металлургия”. 2019;19(3):13–23.
56. Потапов М.Г., Юмабаев А.А., Гуляев Ю.Е. Классификация комплексно-легированных чугунов по температуре разупорядочения кластеров расплава при разработке режимов ВТОР. Актуальные проблемы современной науки, техники и образования. 2022;13(1):31–35.
Об авторах
В. С. ЦепелевРоссия
Владимир Степанович Цепелев, д.т.н., профессор, директор Исследовательского центра физики металлических жидкостей
Россия, 620002, Екатеринбург, ул. Мира, 19
Н. И. Синицин
Россия
Николай Иванович Синицин, к.ф.-м.н., доцент кафедры физики, старший научный сотрудник Исследовательского центра физики металлических жидкостей
Россия, 620002, Екатеринбург, ул. Мира, 19
О. А. Чикова
Россия
Ольга Анатольевна Чикова, д.ф.-м.н., профессор кафедры физики
Россия, 620002, Екатеринбург, ул. Мира, 19
М. Г. Потапов
Россия
Михаил Геннадьевич Потапов, к.т.н., доцент кафедры литейных процессов и материаловедения
Россия, 455000, Челябинская обл., Магнитогорск, пр. Ленина, 38
В. В. Вьюхин
Россия
Владимир Викторович Вьюхин, старший научный сотрудник Исследовательского центра физики металлических жидкостей
Россия, 620002, Екатеринбург, ул. Мира, 19
Рецензия
Для цитирования:
Цепелев В.С., Синицин Н.И., Чикова О.А., Потапов М.Г., Вьюхин В.В. Микрогетерогенное строение жидких чугунов ИЧХ28Н2, ИЧ310Х24М2Ф4ТР. Известия высших учебных заведений. Черная Металлургия. 2024;67(5):579-592. https://doi.org/10.17073/0368-0797-2024-5-579-592
For citation:
Tsepelev V.S., Sinitsin N.I., Chikova O.A., Potapov M.G., V’yukhin V.V. Microheterogeneous structure of liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR. Izvestiya. Ferrous Metallurgy. 2024;67(5):579-592. https://doi.org/10.17073/0368-0797-2024-5-579-592
JATS XML