Scroll to:
Microheterogeneous structure of liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR
https://doi.org/10.17073/0368-0797-2024-5-579-592
Abstract
The paper presents original experimental data on the viscosity and electrical resistivity of liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR. The authors discuss the measurement results within the framework of the concept of metal melts microheterogeneity. Liquid cast iron in a microheterogeneous state is considered as a dispersed system consisting of dispersed Fe – 30 % Cr particles distributed in a Fe – 3 % C dispersion medium. The concept of colloidal microheterogeneity (microheterogeneity) of Fe – C melts was first formulated by Wertman & Samarin more than 80 years ago and found another confirmation in this work. The introduction of theoretical approaches to the rheology of dispersed systems into the analysis of the temperature dependences of the viscosity of microheterogeneous melts made it possible to estimate the parameters of microheterogeneity: the volume fraction and size of dispersed particles. The volume fraction of dispersed particles was determined using the Taylor equation for the viscosity of dispersed systems and size of dispersed particles – within the framework of the theory of absolute reaction rates. Analysis of the temperature dependences of microheterogeneous melts electrical resistivity within the framework of the theory of transport phenomena (in this case, conductivity) in inhomogeneous media (microheterogeneous melts) made it possible to estimate the volume fraction of dispersed particles. The volume fraction of dispersed particles based on data on the electrical resistivity of liquid cast iron was determined using the Odelevsky equation for the inhomogeneous media conductivity. The cluster size was determined by the ratio of the melt electrical resistivity at the liquidus temperature and the analysis temperature, taking into account the known data for the mean free path and the electron scattering coefficient of liquid iron. The volume fraction of dispersed particles in liquid cast iron was 0.2 – 0.1 at the liquidus temperature. With increasing temperature, the volume fraction of dispersed particles decreases. The cluster size in liquid cast iron was about 3 nm at the liquidus temperature, and with increasing temperature the cluster size decreased to 1 – 2 nm. The results obtained are of practical importance: increasing the performance properties of cast iron castings is possible by high-temperature melt treatment (HTMT) in order to change the crystallization conditions and obtain a modified structure. Studies of the microheterogeneous structure of liquid cast irons and assessment of microheterogeneity parameters make it possible to substantiate and propose the optimal HTMT mode in order to improve the performance characteristics of products made of wear-resistant cast irons alloyed with chromium.
Keywords
For citations:
Tsepelev V.S., Sinitsin N.I., Chikova O.A., Potapov M.G., V’yukhin V.V. Microheterogeneous structure of liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR. Izvestiya. Ferrous Metallurgy. 2024;67(5):579-592. https://doi.org/10.17073/0368-0797-2024-5-579-592
Introduction
The development of concepts regarding the microinhomogeneous structure of complex alloyed metallic melts is relevant from a practical perspective for the scientific justification of selecting temperature-time treatment modes. The discussion of structural transitions related to the irreversible destruction of microinhomogeneities when heating a melt to a specific temperature Т\(^*\) for each composition makes this justification possible. Measuring the temperature dependencies of viscosity, density, electrical resistivity, and surface tension of the melt allows determining the temperature Т\(^*\), explaining it through a structural transition caused by the destruction of microinhomogeneities. Numerous experiments have shown that after the structural transition, upon subsequent cooling and crystallization, an ingot with a modified-like structure is formed, which exhibits better mechanical properties. The mechanism of structural transitions in complex alloyed metallic melts involves the destruction of microinhomogeneity not only in structure but also in chemical composition. Anomalies in the temperature and concentration dependencies of the structurally sensitive properties of metallic melts – viscosity, density, electrical resistivity, and surface tension – are caused by changes in the melt structure. Microinhomogeneities, which arise due to the predominant interaction of atoms of the same or different types, correspond to the disruption of short-range order (SRO) in the atomic arrangement and range between 2 – 5 Å. The microinhomogeneous state of metallic melts, which is due to the segregation of atoms of a fluctuational nature without clear interfacial boundaries (clusters), is associated with the disruption of medium-range order (MRO) and ranges between 5 – 20 Å. The microheterogeneous state of the melt, characterized by the presence of dispersed particles enriched with one component suspended in a surrounding medium of a different composition with a distinct interphase surface, corresponds to the disruption of long-range order (LRO) and a range of more than 20 Å [1]. In work [2], the primary focus is on studying impurity effects corresponding to SRO in complex alloyed melts, including investigations of the structure and properties of iron-based melts aimed at improving cast iron and steel production technologies. From a methodological point of view, alongside direct diffraction studies of the structure, a large amount of information is provided by measuring physical properties such as magnetic susceptibility, electrical resistivity, viscosity, and density. For example, magnetic susceptibility together with electrical resistivity forms a pair of electron-sensitive properties that allow assessing the character of short-range order in the system, the distribution of impurities, and alloying effects. Studying the entire set of properties makes it possible to influence the melt by applying small additives. The oscillatory nature of their influence facilitates achieving significant effects through small concentration changes. Moreover, the possibility arises to control the melt structure and the primary crystallization process.
The results of calculations of the radii of microgroupings around carbon atoms in iron and the electronic characteristics of diluted Fe – C – O alloys are presented [2]. Concepts of the cluster structure of metallic liquids, which are due to the segregation of atoms of a fluctuational nature without distinct interphase boundaries (clusters), associated with the disruption of MRO and a range of 5 – 20 Å, are consistently developed by G.V. Tyagunov. The cluster structure of metallic liquids can be described in physical terms if the quantity, composition, and size of clusters, the number of atoms in the clusters, the lifetime of clusters, etc., are known. In this case, the clusters have significant sizes Rcl ≥ (10 – 25)·10\(^–\)10 m [3].
The concept of colloidal, i.e., microheterogeneous, structure of liquid melts, characterized by the presence of dispersed particles enriched with one of the components suspended in a medium of a different composition with a clear interphase surface, corresponds to LRO and a range of more than 20 Å, and has been consistently developed by P.S. Popel concerning eutectic and monotectic melts [4]. The idea of the colloidal structure of eutectic melts was first proposed by Yu.A. Klyachko [5], and later developed by V.M. Zalkin, A.A. Wertman, and A.M. Samarin with colleagues [6 – 9]. They considered eutectic melts as classic colloidal systems with particle dispersity on the order of 1 – 10 nm. In this case, from the perspective of physical chemistry, the melt represents a microheterogeneous system. The terms “microstratified” and “colloidal state” are also used in the same sense. V.M. Zalkin understood eutectic alloys in the liquid state as a thermodynamically stable two-phase state (microemulsions) caused by the slow dissolution of one of the components, gradually transitioning into a state of true (homogeneous) solution, i.e., as lyophilic two-phase systems [7]. The transition from the microemulsion state in this case is reversible: when cooling a true solution, the original microheterogeneity is restored. The existence of a stable two-phase region caused objections from A.A. Wertman due to the violation of the phase rule at the eutectic point [6]. However, the unsoundness of this assertion was pointed out by Ya.I. Frenkel [10]. In the case where one of the phases is dispersed to colloidal scale, an additional degree of freedom arises – the pressure inside the dispersed particles or their radius [11].
The hypothesis of the colloidal microinhomogeneity (microheterogeneity) of Fe – C melts was formulated based on sedimentation experiments by A.A. Wertman and A.M. Samarin. The centrifugation experiments on liquid cast iron conducted by A.A. Wertman, A.M. Samarin, and A.M. Yakobson showed that the radius of carbon atom groupings is close to 10 nm [12]. In the works of A.A. Wertman and A.M. Samarin, colloidal microinhomogeneity (microheterogeneity) of the melt is associated with the presence of a nonequilibrium dispersed phase that gradually dissolves into the dispersion medium [6]. This dynamic (fluctuational) microinhomogeneity has an inherited short-range order structure of solid eutectic phases, with its lifetime comparable to the relaxation time in the arrangement of atoms. The study of the microinhomogeneous (colloidal) state of liquid cast irons led A.A. Wertman and A.M. Samarin to conclude the nonequilibrium nature of this state, which explained the branching of the temperature dependencies of their physical properties obtained in heating and subsequent cooling modes of the melt [13]. V.M. Zalkin proposed limited solubility of carbon in liquid iron, not exceeding 6.5 – 8.5 at. % [7]. At higher carbon concentrations in the melt, spontaneously formed carbon-rich ordered groupings of different types of atoms, structurally similar to cementite, appear as distinct phases. The formation of dispersed cementite particles in liquid alloys occurs within this temperature range during the melting of alloys containing cementite and graphite in their initial structure, as well as during the dissolution of graphite in liquid iron. A rise in carbon content in the melt above 12.4 – 14.2 at. % results in the formation of submicron carbon atom clusters, arranged in a structure similar to graphite [14]. Subsequent development of the understanding of the microheterogeneous state of Fe – C melts views it as a temporary, nonequilibrium state, gradually transitioning into the equilibrium state of a true solution [15]. The concepts of Fe – C melt microheterogeneity enable analyzing the causes for the divergence in the temperature dependencies of their kinematic viscosity and electrical resistivity based on the theory of transport phenomena in inhomogeneous media. Experiments have shown that the size of microregions enriched with like atoms reaches tens of nanometers, significantly exceeding the scale of short-range ordering in melts, allowing the application of known dependencies from the theory of transport phenomena in inhomogeneous media to the calculation of microheterogeneous melt properties [16]. The authors previously used this approach to determine the transition temperatures of Fe – Mn – C melts from the model of isolated inclusions to the model of interpenetrating inclusions [17], as well as the transition temperatures from a heterogeneous system to a homogeneous solution [18].
Based on the concept of the microheterogeneous structure of melts, the theory of suspension viscosity can be applied to analyze the temperature dependencies of kinematic viscosity. The viscosity of a medium containing dispersed inclusions exceeds the viscosity of a pure liquid due to the stresses that arise during particle movement. In this case, one speaks of the effective viscosity of the medium. For dilute dispersed systems, it can be assumed that the interfacial interaction force under slow flow conditions represents Stokes force multiplied by the number of particles in a given volume. This approach was used by Einstein [19; 20] to determine the viscosity of dilute dispersed systems containing solid particles, and by Taylor [19] for dispersions of droplets and bubbles. In another limiting case, when the particle concentration is so high that a close packing regime is realized, filtration theory methods are applied, based on Darcy’s law [21; 22].
Einstein’s theory was first applied to liquid metals to analyze the phenomenon following melting [23]. The Einstein equation has been used multiple times in discussions of viscometric experiments with metallurgical melts. The author of [24] notes that the increase in viscosity upon cooling can be attributed to the enlargement of viscous flow units and crystallization. The viscosity of a suspension is determined by the size of the dispersed phase particles and their quantity in the melt. In the case of liquid steels and cast irons, it has been found that the presence of inclusions in the melt significantly affects its viscosity [25] and resistivity [26].
Alloys with high carbon (up to 4 %) and chromium (up to 30 %) content are characterized by increased strength properties, while parts made from these alloys exhibit higher resistance to wear and oxidation, placing them in the class of wear-resistant cast irons. The high properties of these alloys are due to the presence of a large number of chromium carbides, which are extremely hard. The size, type, and morphology of these carbides determine the wear resistance and impact toughness. The required microstructural characteristics of wear-resistant cast irons are achieved by altering the chemical composition, the crystallization rate, or through special heat treatment [27].
Studies on the influence of vanadium and chromium on the microstructures of white cast irons alloyed with Cr, V, Mn, and Ni have shown that vanadium and chromium increase the overall carbide fraction and the amount of austenite in the matrix, with vanadium carbides (VC) serving as nucleation centers for carbide eutectics [28]. Research on the effect of alloy processing temperature led the authors of [29] to conclude that raising the temperature to 850 °C promotes the formation of secondary carbides and martensite in the microstructure, providing high hardness values. The authors of [30] demonstrated the feasibility of using time-temperature treatment of steel and cast iron in a liquid state for the production of critical castings with high resistance to abrasive and impact-abrasive wear. Specifically, for steel grade 4Kh5V2FSL, high-temperature melt treatment increased the strength properties by 36 %, while maintaining high wear resistance. However, for cast iron IChKh28N2, the alloy with the highest abrasive and impact-abrasive wear resistance was obtained by holding at 1420 °C. Holding at 1520 °C resulted in a reduction of the microhardness of the matrix and eutectics, but increased the microhardness of individual chromium carbides by 400 HV.
A rational processing mode for obtaining IChKh28N2 cast iron was proposed: heating the melt to 1470 °C, holding for 15 min, cooling to the pouring temperature, followed by the introduction of (Ca, Sr)CO3 and BFT-1 ligature in amounts of 3 and 4 kg/ton, respectively. The application of the developed cast iron melt treatment method also positively influenced fluidity, a key casting property. The effect of boron on the crystallization conditions of heat-resistant and wear-resistant cast irons in the Fe – C – Cr – Mn – Ni – Ti – Al – Nb system was studied [31].
It was found that the hardness of the matrix of high-chromium cast irons increased after heat treatment due to the combined effect of secondary carbide precipitation Me23C6 during destabilization and the austenite-martensite transformation during quenching. Kinetic calculations of the destabilization process showed that secondary carbides Мe7С3 precipitate first, reaching a maximum at 850 °C. Upon further heating to 980 °C and holding at this temperature, they are fully transformed into Me23C6 [32]. As the destabilization temperature increases to 1000 °C, the number, volume, and size of secondary carbides (up to 2.22 μm) increase. At 1050 °C and a 3 h holding time, the size of secondary carbides significantly decreases, with a high density of distribution in the matrix phase. At this stage, the samples exhibit better corrosion resistance [33]. The carbon content in the matrix, depending on the destabilization temperature and the subsequent dissolution of eutectic carbides, controls the martensite formation onset temperature and has a dominant effect on bulk hardness [34].
The work [35] presents data on the phase composition and structure formation of alloys and oxide layers, the distribution of elements across the structural components of the alloy and the oxidation surface to the depth of the oxide and sub-oxide layers, as well as changes in wear resistance, oxidation resistance, stability, and mechanical properties of cast irons in the Cr – Mn – Ni – Ti – Al – Nb system, depending on the aluminum and niobium content and the heat retention capacity of the casting mold.
Overheating liquid cast iron above 1500 °C reduces the size of primary carbides. Within the temperature range between the liquidus and solidus lines, recrystallization of primary carbides (Cr, Fe)7C3 was observed, significantly reducing chromium content and increasing iron content in them [36]. Structural and property changes in hypereutectic chromium cast irons after heat treatment were found, which, according to the authors of [36], are associated with the existence of compositionally stable clusters in the melt from the melting point to approximately 1500 °C. This is due to the high affinity of chromium and carbon and the presence of refractory carbide Cr7C3 . It was found that heat treatment of the melt in the temperature range of 1260 – 1320 °C (between the liquidus and solidus lines) increases wear resistance, while increasing the treatment temperature leads to a decrease in the wear resistance of the ingots. Heat treatment of fine-grained castings from hypereutectic chromium iron in the temperature range between the liquidus and solidus causes recrystallization of primary carbide crystals (Cr, Fe)7C3 , altering their composition, shape, and slightly increasing their size. In this case, the fraction of primary carbides increases, and the fraction of eutectic carbides decreases as the temperature of heat treatment is reduced.
The microstructure of Fe – Cr – C ingots includes primary and secondary dendrites of the Fe – Cr solid solution, decorated with complex Me23C6 and Me7C3 [37]. The microstructure of the Fe – 34Cr – 4.5C alloy consists of a chromium-rich austenitic matrix with Me7C3 , carbides, which persists at temperatures slightly above 1150 °C and is metastable in nature [38]. Based on this, it is assumed that in the liquid state, the Fe – Cr – C melt, in the context of microheterogeneous structure, can be understood as Fe – Cr dispersed particles distributed in an Fe – C dispersion medium.
Thus, liquid cast iron can be considered a colloidal system consisting of a dispersion medium and inclusions. In this case, the concepts of the theory of transport phenomena in inhomogeneous media and the theory of suspension viscosity are applicable to such systems. The objective of this work is to analyze experimental data on kinematic viscosity and electrical resistivity to determine the volume fraction of dispersed particles in IChKh28N2 and ICh310Kh24M2F4TR cast iron melts. To determine the volume fraction of dispersed particles, it is proposed to use established concepts from the theory of viscous flow of suspensions and the theory of transport phenomena in inhomogeneous media.
Research methods
Experimental methods
The objects of the study were selected samples of industrial wear-resistant cast iron alloys IChKh28N2, alloyed with Cr and Ni, as well as ICh310Kh24M2F4TR, alloyed with Cr, Mo, V, and Ti, produced under laboratory conditions while adhering to the technology of casting wear-resistant cast irons. The chemical composition of the samples was determined using a spark source spectrometer (SPECTROMAXx, SPECTRO Analytical Instruments GmbH, Germany) and is presented in Table. Under laboratory conditions, the electrical resistivity and kinematic viscosity of these samples were studied.
The electrical resistivity ρ of the wear-resistant cast iron alloys in the liquid state was measured using Regel’s method, which involves the twist angle of a container with the test sample under the influence of a rotating magnetic field, with a sample height-to-diameter ratio of h/d ≈ 1. A.R. Regel demonstrated that the twist angle φ of the suspended system is proportional to the electrical conductivity of the metal if the radius of the cylindrical sample is comparable to its height [39 – 41]. Measurements of the electrical resistivity were conducted using an original setup described in [42].
The kinematic viscosity ν of the wear-resistant cast irons in the liquid state was measured using the method of torsional oscillations of a crucible containing the melt in a single-ended configuration [43; 44]. The kinematic viscosity was determined by observing the damping of the torsional oscillations of the crucible with the melt, recording the oscillation period and the logarithmic decrement of the damping. The kinematic viscosity of the melt was then calculated. The height of the liquid alloy must be 2H ≥ 1.85R relative to the radius of the crucible, to ensure full damping of the viscous waves propagating from the bottom of the crucible to the free surface.
Measurements of electrical resistivity and kinematic viscosity were performed over a temperature range from TL to 1650 °C. The working chamber was pre-evacuated to 0.001 Pa, after which helium was introduced to a pressure of ~105 Pa. The samples were held in an inert atmosphere for 10 – 15 min at the liquidus temperature TL , followed by heating to 1650 °C in increments of 30 – 40 °C. The systematic error in the measurement of ρ and ν was 3 %, while the random error, determining the scatter of points in a single experiment with a confidence probability of p = 0.95 did not exceed 1.5 %.
The liquidus temperature was determined based on viscometric studies by the sharp change in the logarithmic decrement of the damping torsional oscillations of the crucible with the melt, according to the method described in [45].
Calculation of the volume fraction of microheterogeneous inclusions
To determine the volume fraction of inclusions in liquid cast irons, an approach was used based on the theory of conductivity in inhomogeneous media and theoretical models of suspension viscosity. In this case, the liquid cast iron was considered a microheterogeneous system, in which dispersed particles are distributed in a dispersion medium. For the IChKh28N2 and ICh310Kh24M2F4TR alloys in the liquid state, the dispersion medium is assumed to be the Fe – 3 % С melt, while the dispersed particles consist of the Fe – 30 % Cr melt.
In analyzing the results of the viscometric experiment on liquid cast irons to estimate the volume fraction φ of the dispersed phase in the melts, Taylor’s equation [19] for dispersions of droplets and bubbles was applied:
| \[{\eta _\varphi } = {\eta _2}\left[ {1 + 2.5\varphi \left( {\frac{{{\eta _1} + 0.4{\eta _2}}}{{{\eta _1} + {\eta _2}}}} \right)} \right],\] | (1) |
where ηφ is the effective viscosity of the dispersion; η1 and η2 are the viscosities of the dispersed phase and the continuous phase, respectively.
Based on the experimental data on the temperature dependence of kinematic viscosity ν, the dynamic viscosity η of the liquid cast iron was determined from the equation η = νd. The density d of the liquid cast iron was determined from an additive dependence on the content of each component in the melt Xl and its temperature-dependent density dl .
In the liquid state, the melt was understood as a microheterogeneous system consisting of Fe – 30 % Cr dispersed particles and an Fe – 3 % C dispersion medium. The dynamic viscosity of such a system can be estimated using Taylor’s equation (1)
| \[{\eta _{ef}} = {\eta _{{\rm{Fe}} - {\rm{C}}}}\left[ {1 + 2.5\varphi \left( {\frac{{{\eta _{{\rm{Fe}} - {\rm{Cr}}}} + 0.4{\eta _{{\rm{Fe}} - {\rm{C}}}}}}{{{\eta _{{\rm{Fe}} - {\rm{C}}}} + {\eta _{{\rm{Fe}} - {\rm{Cr}}}}}}} \right)} \right],\] | (2) |
where ηef is the viscosity of the liquid cast iron;; ηFe – C is the viscosity of the Fe – C melt, and ηFe – Cr is the viscosity of the Fe – Cr melt.
Experimental data on the viscosity of Fe – C melts with carbon content up to 5 % were obtained by the authors of [46] and modeled using molecular dynamics in [47]. The viscosity of Fe – Cr melts up to 40 at. % and Fe85 – xCr15Cx (x = 10 – 17 at. %) was studied in [48; 49]. The known experimental data on the temperature dependence of the viscosity of Fe – C, Fe – Cr melts, and liquid cast irons were approximated by an exponential expression of the form
| \[\eta = A\exp \left( {\frac{b}{T}} \right).\] | (3) |
To determine the volume fraction of dispersed Fe – Cr particles in the liquid cast iron, the following equation was derived
| \[{\eta _{ef}} - {\eta _{{\rm{Fe}} - {\rm{C}}}}\left[ {1 + 2.5\varphi \left( {\frac{{{\eta _{{\rm{Fe}} - {\rm{Cr}}}} + 0.4{\eta _{{\rm{Fe}} - {\rm{C}}}}}}{{{\eta _{{\rm{Fe}} - {\rm{C}}}} + {\eta _{{\rm{Fe}} - {\rm{Cr}}}}}}} \right)} \right] = 0.\] | (4) |
In analyzing the results of the resistometric experiment on liquid cast irons, to estimate the volume fraction φ of the dispersed phase in the melts, the Odelevsky equation [50] was applied, which relates the conductivity σ of a two-phase system to the conductivities of the solvent σs and the dispersed particles σp :
| \[\begin{array}{c}\sigma = \frac{{2{\sigma _s} - {\sigma _p} + \varphi (3{\sigma _p} + {\sigma _s})}}{4} + \\ + \sqrt {{{\left( {\frac{{2{\sigma _s} - {\sigma _p} + \varphi (3{\sigma _p} + {\sigma _s})}}{4}} \right)}^2} + \frac{{{\sigma _s}{\sigma _p}}}{2}} .\end{array}\] | (5) |
Experimental data on the resistivity of Fe – C melts with carbon content up to 4.2 % were obtained by the authors of [51]. The experimental data on the resistivity of Fe – Cr melts over a wide range of compositions were studied in [52]. The known experimental data on the temperature dependence of the resistivity of the melts were approximated by linear dependencies.
To determine the volume fraction of Fe – Cr dispersed particles in the liquid cast iron, the following equation was derived
| \[\begin{array}{c}{\sigma _{ef}} - \frac{{2{\sigma _s} - {\sigma _p} + \varphi (3{\sigma _p} + {\sigma _s})}}{4} + \\ + \sqrt {{{\left( {\frac{{2{\sigma _s} - {\sigma _p} + \varphi (3{\sigma _p} + {\sigma _s})}}{4}} \right)}^2} + \frac{{{\sigma _s}{\sigma _p}}}{2}} = 0,\end{array}\] | (6) |
where \({\sigma _{ef}} = \frac{1}{{{\rho _{ef}}}}\) is the conductivity of the liquid cast iron; \({\sigma _s} = \frac{1}{{{\rho _{{\rm{Fe}} - {\rm{C}}}}}}\) is the conductivity of the Fe – C melt; \({\sigma _p} = \frac{1}{{{\rho _{{\rm{Fe}} - {\rm{Cr}}}}}}\) is the conductivity of the Fe – Cr melt.
Equations (4) and (6), given the known properties of the binary systems Fe – C (ηFe – C , σs ), Fe – Cr (ηFe – Cr , σp ) and the liquid cast iron (ηef , σef ) were solved for the volume fraction of inclusions (φ) using the fsolve function from the SciPy library within the temperature range of 1310 – 1650 °С.
The molar fraction of the dispersed particles was determined from the obtained data on the volume fraction of inclusions using the expression
| \[{m_i} = \frac{{{n_i}}}{{{n_\Sigma }}},{\rm{ }}{n_i} = \frac{{{\varphi _i}}}{{{M_i}}}{d_i},\] | (7) |
where mi , ni , φi , Mi , di are the molar fraction, the number of moles per unit volume, the volume fraction, the molar mass, and the density of the i\(^{th}\) component, respectively.
Results and discussion
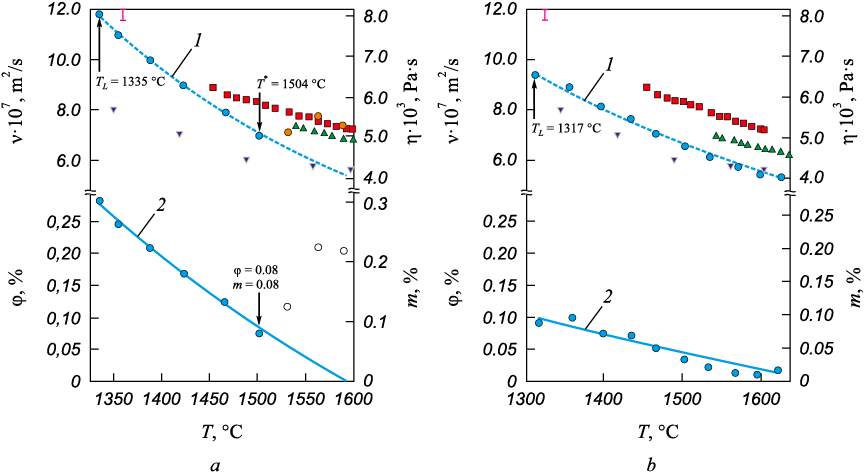
The results of the experimental investigation of kinematic viscosity in the temperature range from TL to 1650 °C for IChKh28N2 and ICh310Kh24M2F4TR liquid cast irons are presented in Fig. 1. The values of kinematic viscosity obtained in this study are consistent with the viscosity data of the Fe – 15 at. % Cr – 10 at. % С melt reported by the authors of [48]. On the right axis of the same graph (Fig. 1) the dynamic viscosity values are shown. Under the temperature dependence of kinematic viscosity, the experimental and calculated data on the volume (right axis of the graph) and molar (left axis of the graph) fractions of heterogeneous inclusions in the liquid cast irons are presented. Based on the viscometric study, the liquidus temperatures for the liquid cast irons were determined using the method described in [45]. The liquidus temperatures are indicated on the temperature dependencies of kinematic viscosity.
Fig. 1. Temperature dependences of kinematic viscosity (ν), dynamic viscosity (η), volumetric (φ) |
In analyzing the results of the viscometric experiment on liquid cast irons to estimate the volume fraction φ of the dispersed phase in the melts, the approach proposed by A. Einstein for describing the viscosity of dispersed systems was applied [19; 20]. A. Einstein considers the case of constrained flow around a system of spherical particles by a liquid flow and introduces the concept of the effective viscosity of the medium. The velocity of particle movement in a constrained flow depends not only on their size, shape, and the physicochemical properties of the medium but also on the volume concentration φ. The dependence on the volume concentration is caused by hydrodynamic interactions between the particles. The velocity of a particle in a constrained flow is generally lower than that of an isolated particle. The viscosity of a medium containing dispersed inclusions exceeds the viscosity of a pure liquid due to the stresses that arise during particle movement. In this case, the term “effective viscosity of the medium” is used. A strict description of the laws governing constrained particle motion in a viscous flow does not yet exist. For the case of dilute dispersed systems, this approach was used by Einstein [19] to determine the effective viscosity of a medium containing solid particles, and by Taylor [19] for determining the dispersion of droplets and bubbles. The melt, as a microheterogeneous system, was understood as dispersed particles enriched with Cr (Fe – 30 % Cr), distributed in a dispersion medium of Fe – 3 % C. Based on the known values of the viscosities of Fe – Cr and Fe – C melts [46 – 48] and the experimental data on the viscosity of the dispersed system, the values of the volume fraction of the dispersed particles (Fe – 30 % Cr) in liquid cast irons were obtained by solving equation (4). The calculated values of the volume fraction of inclusions (Fig. 1) were derived from the temperature dependencies of the kinematic viscosity of Fe – 3 % C, Fe – 30 % Cr and liquid cast irons, approximated by equation (3). The values of the volume fraction of dispersed particles, marked with the symbol ![]() in Fig. 1, were obtained from the experimental data on the kinematic viscosity of liquid cast irons and the approximated values of the kinematic viscosity of the dispersed particles (Fe – 30 % Cr) and the dispersion medium (Fe – 3 % C) from equation (3). The molar fraction of the dispersed particles was determined from the obtained data on the volume fraction using equation (7).
in Fig. 1, were obtained from the experimental data on the kinematic viscosity of liquid cast irons and the approximated values of the kinematic viscosity of the dispersed particles (Fe – 30 % Cr) and the dispersion medium (Fe – 3 % C) from equation (3). The molar fraction of the dispersed particles was determined from the obtained data on the volume fraction using equation (7).
The dependence of the kinematic viscosity on temperature for the liquid cast iron IChKh28N2 in the range from TL to 1504 °C follows an exponential law and is consistent with the Arrhenius equation. In the same temperature range, the volume and molar fractions decrease from 0.28 (0.30) to 0.08 (0.08). However, at temperatures above 1504 °C, an anomalous increase in kinematic viscosity with rising temperature (marked by the symbol ![]() in Fig. 1, а) was observed, which was also accompanied by an abnormal increase in the volume fraction of dispersed particles in the liquid cast iron, deviating from the calculated curve. This behavior may be related to structural changes in the melt. As the dispersed particles dissolve, the melt transitions into a more homogeneous solution, changing the chemical composition of the dispersed phase, which leads to the anomalous increase in viscosity. In this case, equation (4) is not applicable for describing the viscous flow of a homogeneous system.
in Fig. 1, а) was observed, which was also accompanied by an abnormal increase in the volume fraction of dispersed particles in the liquid cast iron, deviating from the calculated curve. This behavior may be related to structural changes in the melt. As the dispersed particles dissolve, the melt transitions into a more homogeneous solution, changing the chemical composition of the dispersed phase, which leads to the anomalous increase in viscosity. In this case, equation (4) is not applicable for describing the viscous flow of a homogeneous system.
The kinematic viscosity for the liquid cast iron ICh310Kh24M2F4TR decreases monotonically with increasing temperature, and the volume (molar) fraction of heterogeneous inclusions in the liquid cast iron also decreases monotonically, from 0.10 (0.10) at the liquidus temperature to 0.01 (0.01). This indicates the dissolution of heterogeneous inclusions in the melt as the temperature rises.
Based on the data from the viscometric experiment, an estimate of the size of the structural unit responsible for viscous flow in the melts of IChKh28N2 and ICh310Kh24M2F4TR cast irons was made. The method proposed in [53] was used to determine the size of the structural unit of viscous flow. The temperature dependence of the kinematic viscosity is expressed as
| \[\nu = \frac{{B{T^{1/2}}}}{{{s^{1/2}}}}\exp \left( {\frac{\varepsilon }{{kT}}} \right),\] | (8) |
where \(B = \frac{\pi }{4}{\left( {\frac{k}{{3d}}} \right)^{1/2}};\) s is the size of the dispersed particles.
It was found that for the IChKh28N2 melt, s = 1.3 nm, and for the ICh310Kh24M2F4TR melt, s = 1.4 nm, which is of the same order of magnitude as the data obtained for the liquid steel 110G13L in [54].
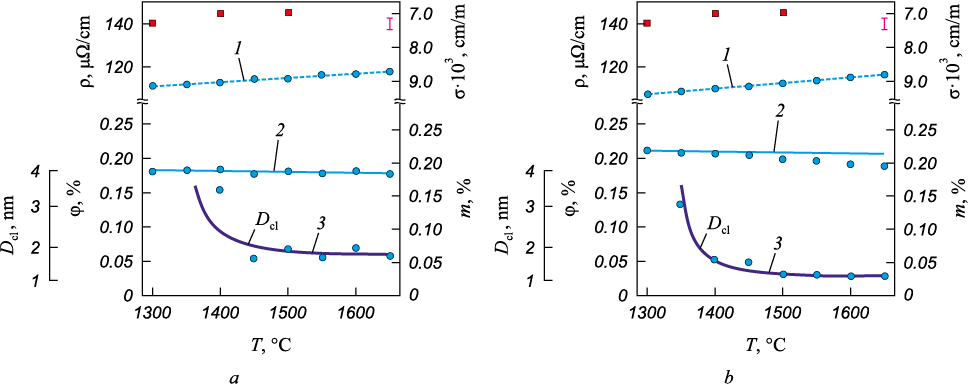
The results of the resistometric study of the liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR are presented in Fig. 2. The values of electrical resistivity are shown on the left axis of the graph, while the values of electrical conductivity of the liquid cast irons are shown on the right axis. Below the experimental data on resistivity (conductivity), the obtained values of the volume (left axis) and molar (right axis) fractions of dispersed particles in the liquid cast irons are presented.
Fig. 2. Temperature dependences of electrical resistivity (ρ), conductivity (σ), volume (φ) |
The analysis of the resistivity measurements was based on the theory of conductivity in inhomogeneous media. The liquid cast iron was considered as dispersed particles enriched with Cr (Fe – 30 % Cr), distributed in a dispersion medium of Fe – 3 % C. Using the framework of conductivity in inhomogeneous media, the volume fraction of dispersed particles in the liquid cast irons was determined by solving equation (6), based on the known data on the conductivity (1/ρ) of dispersed particles (Fe – 30 % Cr) [52], the dispersion medium (Fe – 3 % C) [51]], and the experimental data on the conductivity of the liquid cast iron. The calculated values of the volume fraction (Fig. 2) were obtained from the linear approximation of the known experimental data on the temperature dependencies of the conductivity of Fe – 3 % C, Fe – 30 % Cr, and the liquid cast irons. The volume fractions of dispersed particles in Fig. 2, were derived from the experimental data on the conductivity of the liquid cast irons and the linear approximation of the conductivity values of the dispersed particles (Fe – 30 % Cr) [52] and the dispersion medium (Fe – 3 % C) [51]. Near the melting temperature, the volume (molar) fraction of dispersed particles is 0.18 (0.19) for IChKh28N2 and 0.21 (0.22) for ICh310Kh24M2F4TR. As the temperature increases, the volume (molar) fraction of dispersed particles decreases slightly.
In [55], the following expression was proposed for microinhomogeneous metallic melts:
| \[\ln \left( {\frac{\rho }{{{\rho _L}}}} \right) = \frac{{{l_{\rm{ir}}}}}{{{D_{{\rm{cl}}}}}}\ln \left( {\frac{1}{r}} \right),\] | (9) |
where ρL and ρ are the specific resistivity of liquid iron at the liquidus temperature and the analysis temperature, respectively; lir is the mean free path of electrons in liquid iron; Dcl is the cluster diameter; r is the electron scattering coefficient.
The mean free path of electrons in liquid iron decreases from 4.63 to 4.28 Å when the melt is heated from 1400 to 1600 °C. Since the scattering coefficient varies within the range 0 < r < 1, equation (4) implies that as the cluster size decreases, the resistivity of the melt should increase. Calculations showed that at t = 1600 °С, r = 0.97, and at t = 1800 °С r = 0.86, meaning that as the temperature rises, r decreases, and ρ increases. The cluster size determined by equation (8) (Fig. 2) for IChKh28N2 is 3.4 nm at 1400 °C and decreases to 1.7 nm at temperatures above 1600 °C. For ICh310Kh24M2F4TR, the cluster size is 1.7 nm at 1400 °C and decreases to 1.2 nm at temperatures above 1600 °C. Therefore, the experimentally observed increase in the resistivity of liquid iron with increasing temperature is likely not related to changes in the melt structure at the atomic level, but rather to a decrease in the number of conduction electrons. This is explained by the increased number of electrons participating in the strengthening of interatomic bonds and ensuring the stability of the clusters as they become smaller with increasing temperature.
In conclusion, based on the results of viscometric and resistometric studies, it was established that liquid cast irons represent a dispersed system, containing, near the melting temperature, a volume fraction of dispersed particles of 0.28 and 0.10, according to viscometry, for liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR, respectively, corresponding to particle sizes ranging from 100 to 10 nm. According to resistometry data, the volume fraction of dispersed particles is about 0.20 for the liquid cast irons and does not significantly change with increasing temperature. A volume fraction of 0.20 corresponds to dispersed particles with a size of about 10 nm. According to estimates made by the authors of [56] within the framework of the quasi-chemical model of microinhomogeneous structure for complex-alloyed melts [1], the molar fraction of clusters in the liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR is 0.43 at the liquidus temperature, which is significantly higher than the values obtained in this study. Based on this, liquid cast iron can be considered a microheterogeneous system. Increasing the temperature leads to a reduction in the volume fraction of dispersed particles, consistent with the concept of the breakdown of the microheterogeneous state as the liquid melt is overheated beyond a certain temperature.
Conclusions
The study presents experimental data on the temperature dependencies of kinematic viscosity and electrical resistivity of liquid cast irons in the range from the liquidus temperature TL to 1650 °C. Liquid cast iron in the molten state was understood as a microheterogeneous system, characterized by the presence of dispersed particles enriched with one of the components.
Based on the data on the kinematic viscosity of liquid cast irons, the volume fraction of heterogeneous inclusions was determined using the concept of viscous flow in dilute dispersed systems. It was found that the volume fraction of dispersed particles in liquid cast irons near the melting point is 0.28 for IChKh28N2 and 0.1 for ICh310Kh24M2F4TR. A volume fraction of 0.28 corresponds to dispersed particle sizes of ~100 nm, while 0.1 corresponds to particle sizes of ~10 nm. The obtained particle sizes align with the concept of the microheterogeneous structure of liquid cast irons. As the temperature increases, the volume fraction of dispersed particles decreases monotonously to values of 0.08 – 0.01.
The volume fraction of dispersed particles was also determined based on the data on the electrical resistivity of liquid cast irons, which amounted to 0.18 for IChKh28N2 and 0.21 for ICh310Kh24M2F4TR. The obtained volume fractions correspond to dispersed particle sizes of ~10 nm. With increasing temperature, the volume fraction of dispersed particles decreases only slightly.
It is known that heat treatment of the melt, aimed at breaking down the microheterogeneous structure, leads to a modification of the crystallized ingot’s structure by altering the crystallization conditions. However, the authors of [30; 36] found that overheating of chromium cast iron melts reduces the wear resistance of the ingots. The authors of [36] discovered that overheating the melt above 1500 °C leads to the destruction of compositionally stable clusters in the melt, which results in changes in the structure and properties of hypereutectic chromium cast irons after heat treatment. To improve the performance properties, the authors of [30] propose the introduction of additional modifiers before casting the iron after time-temperature melt treatment, while the authors of [36] found that wear resistance can be enhanced by heat treatment between the liquidus and solidus temperatures. Thus, the study of chromium cast iron melts in the liquid state from the perspective of their microinhomogeneous structure will help to advance the understanding of processes occurring in the liquid state and develop an optimal melt heat treatment mode to improve the performance characteristics.
References
1. Chikova O.A. Structural transitions in complexly alloyed melts. Izvestiya. Ferrous Metallurgy. 2020;63(3–4): 261–270. (In Russ.). https://doi.org/10.17073/0368-0797-2020-3-4-261-270
2. Sidorov V.E., Son L.D. Research of melts as a basis for improvement of technologies of ferrous metallurgy. Chernye Metally. 2023;(3):58–64. (In Russ.). https://doi.org/10.17580/chm.2023.03.10
3. Tyagunov G.V., Baryshev E.E., Tyagunov A.G., Mushnikov V.S., Kostina T.K. On some structuring features of metallic fluids. Bulletin of South Ural state university. Series “Metallurgy”. 2018;18(3):16–25. (In Russ.). https://doi.org/10.14529/met180302
4. Popel P.S. Metastable microheterogenicity of melts in systems with eutectic and monotectic and its effect on the alloy structure after solidification. Rasplavy. 2005(1):22–48. (In Russ.).
5. Klyachko Yu.A. Experience of Colloidal Chemical Research of Metals. Moscow: Publishing House of the Voroshilov Academy; 1935:92. (In Russ.).
6. Vertman A.A. Microheterogenicity of metal melts regulation of castings properties. Fizika i khimiya obrabotki materialov. 1967;(3):132–141. (In Russ.).
7. Zalkin V.M. Nature of Eutectic Alloys and Effect of Contact Melting. Moscow: Metallurgiya; 1987:52. (In Russ.).
8. Zalkin V.M. On two theories describing the initial stage of contact melting. Rasplavy. 2004;(2):93–95. (In Russ.).
9. Zalkin V.M. On microheterogeneous structure of eutectic alloys (solutions) in liquid state (on the 120th anniversary of the term “eutectic”). Journal of Physical Chemistry. 2005;79(4):763–765. (In Russ.).
10. Frenkel’ Ya.I. Statistical Physics. Moscow: Publishing House of the USSR Academy of Sciences; 1948:760. (In Russ.).
11. Morozov D.I., Trusov L.I., Lapovok V.N. Physical Phenomena in Ultrafine Media. Moscow: Energoatomizdat; 1984:224. (In Russ.).
12. Vertman A.A., Samarin A.M., Yakobson A.M. On structure of liquid eutectic. Izv. AS USSR. OTN. Metallurgiya i toplivo. 1960;(3):17–21. (In Russ.).
13. Vertman A.A., Samarin A.M., Turovskii B.M. Structure of liquid alloys of ironcarbon system. Izv. AS USSR. OTN. Metallurgiya i toplivo. 1960;(6):123–129. (In Russ.).
14. Vertman A.A., Samarin A.M. Properties of Iron Melts. Moscow: Nauka; 1969:197. (In Russ.).
15. Brodova I.G., Zamyatin V.M., Popel’ P.S., Esin V.O., Baum B.A., Moiseev A.I., Korshunov I.P., Topchii A.L., Tikhomirov Y.G., Polents I.V. Conditions of metastable phases formation during solidification of Al-Zr alloys. Rasplavy. 1988;(6–2):23–27. (In Russ.).
16. Dul’nev G.N., Novikov V.V. Transfer Processes in Inhomogeneous Media. Leningrad: Energoatomizdat; 1991:248. (In Russ.).
17. Sinitsin N.I., Chikova O.A., V’yukhin V.V. Resistivity of Fe–Mn–C melts. Inorganic Materials. 2021;57(1):86–93. https://doi.org/10.1134/S002016852101012X
18. Chikova O.A., Sinitsin N.I., V’yukhin V.V. Electrical resistivity of liquid Fe–Mn alloys. Russian Physics Journal. 2021;64:1039–1046. https://doi.org/10.1007/s11182-021-02426-y
19. Bibik E.E. Rheology of Dispersed Systems. Leningrad: Leningrad University; 1981:172. (In Russ.).
20. Happel J., Brenner H. Low Reynolds Number Hydrodynamics. Springer Dordrecht; 1983:553. https://doi.org/10.1007/978-94-009-8352-6
21. Ur’ev N.P., Highly Concentrated Dispersed Systems. Moscow: Khimiya; 1980:149. (In Russ.).
22. Rheology. Theory and Applications. Eirich F.R. ed. Vol. 1. New York: Acad. Press; 1956:540.
23. Glazov V.M., Timoshenko V.I. Analysis of the phenomenon of post-melting in semiconductor melts based on the cluster model. Journal of Physical Chemistry. 1981;55(6):1148–1452. (In Russ.).
24. Morozov A.A. Technological properties and structure of titanate melts. Tsvetnye metally. 2002;(8):60–63. (In Russ.).
25. Borovykh M.A., V’yukhin V.V., Chikova O.A., Tsepelev V.S. The influence of defects on the ductility of liquid steel 32G1 and 32G2. Izvestiya. Ferrous Metallurgy. 2015;58(6): 402–406. (In Russ.). https://doi.org/10.17073/0368-0797-2015-6-402-406
26. Borovykh M.A., Chikova O.A., Tsepelev V.S., V’yukhin V.V. Effect of heat treatment conditions on electrical resistivity of 35KhGF molten steel. Izvestiya. Ferrous Metallurgy. 2018;61(3):237–243. (In Russ.). https://doi.org/10.17073/0368-0797-2018-3-237-243
27. Abdel-Aziz K., El-Shennawy M., Omar A. Microstructural characteristics and mechanical properties of heat treated high-Cr white cast iron alloys. International Journal of Applied Engineering Research. 2017;12(14):4675–4686.
28. Efremenko V.G., Shimizu K., Cheiliakh A.P., Kozarevskaya T.V., Kusumoto K., Yamamoto K. Effect of vanadium and chromium on the microstructural features of V-Cr-Mn-Ni spheroidal carbide cast irons. International Journal of Minerals Metallurgy and Materials. 2014;21(11):1096–1108. https://doi.org/10.1007/s12613-014-1014-6
29. Karantzalis A.E., Lekatou A., Kapoglou A., Mavros H., Dracopoulos V. Phase transformations and microstructural observations during subcritical heat treatments of a high-chromium cast iron. Journal of Materials Engineering and Performance. 2012;21(6):1030–1039. https://doi.org/10.1007/s11665-011-9995-z
30. Kolokoltsev V.M., Mikhalkina I.V., Shevchenko A.V. High temperature treatment of special steel and cast iron melts. Liteishchik Rossii. 2016;(9):18–23. (In Russ.).
31. Kolokol’tsev V.M., Petrochenko E.V., Molochkova O.S. Influence of boron modification and cooling conditions during solidification on structural and phase state of heat- and wear-resistant white cast iron. Izvestiya. Ferrous Metallurgy. 2019;62(11):887–893. (In Russ.). https://doi.org/10.17073/0368-0797-2019-11-887-893
32. Guitar M.A., Nayak U.P., Britz D., Mücklich F. The effect of thermal processing and chemical composition on secondary carbide precipitation and hardness in high-chromium cast irons. International Journal of Metalcasting. 2020;14(3):755–765. https://doi.org/10.1007/s40962-020-00407-4
33. Quyen Hoang Thi Ngoc, Ngoc Tran Vu Diem, Viet Nguyen Hoang, Hai Nguyen Hong, Ha Le Thu, Nam Nguyen Duong. Effect of residual stress distribution on the formation, growth and coalescence of voids of 27Cr white cast iron under impact loading. Materials Transactions. 2022;63(2):170–175. https://doi.org/10.2320/matertrans.MT-M2021161
34. Le Nué C., Corujeira Gallo S., Vahid A., Wang J., Taherishargh M., Attar H., Fabijanic D., Barnett M. Destabilization treatment and its influence on microstructure and matrix hardness of high-Cr cast iron. Metallurgical and Materials Transactions A. 2023;54(12):4952–4965. https://doi.org/10.1007/s11661-023-07216-4
35. Kolokoltsev V.M., Petrochenko E.V., Molochkova O.S. Influence of aluminium and niobium alloying on phase composition, structure and properties of heat- and wear-resistant cast iron of Cr-Mn-Ni-Ti system. CIS Iron and Steel Review. 2021;(2):55–60. https://doi.org/10.17580/cisisr.2021.02.10
36. Panichkin A., Wieleba W., Kenzhegulov A., Uskenbayeva A., Mamaeva A., Imbarova A., Kvyatkovskii S., Kasenova B. Effect of thermal treatment of chromium iron melts on the structure and properties of castings. Materials Research Express. 2023;10(8):086502. https://doi.org/10.1088/2053-1591/acead7
37. Wieczerzak K.K., Bała P., Stępień M., Cios G., Kozieł T. The Characterization of Cast Fe-Cr-C Alloy. Archives of Metallurgy and Materials. 2015;60(2):779–782. https://doi.org/10.1515/amm-2015-0206
38. Svensson L.-E., Gretoft B., Ulander B., Bhadeshia H.K.D.H. Fe-Cr-C hardfacing alloys for high-temperature applications. Journal of Materials Sci. 1986;21(3):1015–1019. https://doi.org/10.1007/BF01117388
39. Tsepelev V.S. Physics of Amorphous and Nanocrystalline Metallic Melts: Methodology of Analysis: Monography. Yekaterinburg: Ural Publishing House university; 2023:208. (In Russ.).
40. Regel A.R. An electrodeless method for measuring electrical conductivity and possibility of its application to problems of physico-chemical analysis. Journal of Inorganic Chemistry. 1956;1(6):1271–1277. (In Russ.).
41. Ryabina A.V., Kononenko V.I., Razhabov A.A. Nonelectrode method of measurement electrical resistivity of metals in solid and liquid states and installation for its realization. Rasplavy. 2009(1):36–42. (In Russ.).
42. Tyagunov G.V., Baum B.A., Tsepelev V.S., Tyagunov A.G., Vlokh A.N. Measurement of electrical resistivity by rotating magnetic field method. Zavodskaya laboratoriya. 2003;69(2):36–38. (In Russ.).
43. Shvidkovskii E.G. Some Issues of Molten Metals Viscosity. Moscow: Gostekhizdat; 1955:206. (In Russ.).
44. Konashkov V.V., Tsepelev V.S., V’yukhin V.V., Povodator A.M., Podol’skaya A.I. A computer-aided plant for studying the kinematic viscosity of high-temperature metallic melts. Instruments and Experimental Techniques. 2011; 54(2):284–285. https://doi.org/10.1134/S0020441211020187
45. Chikova O.A., Shmakova K.Yu., Tsepelev V.S. Determination of phase equilibrium temperatures of high-entropy metal alloys by the viscometric method. Metaly. 2016;(2):54–59. (In Russ.).
46. Tanaka T., Hara S. Surface tension and viscosity of liquid iron alloys. Materia Japan. 1997;36(1):47–54.
47. Feng G., Jiao K., Zhang J., Gao S. High-temperature viscosity of iron-carbon melts based on liquid structure: The effect of carbon content and temperature. Journal of Molecular Liquids. 2021;330:115603. https://doi.org/10.1016/j.molliq.2021.115603
48. Kamaeva L.V., Sterkhova I.V., Lad’yanov V.I. Viscosity and supercooling of Fe-Cr (≤40 at % Cr) melts. Inorganic Materials. 2012;48(3):318–324. https://doi.org/10.1134/S0020168512030089
49. Sterkhova I.V., Kamaeva L.V., Lad`yanov V.I. Viscosity of the eutectic Fe85-xCr15Cx (x = 10–17) melts. Physics and Chemistry of Liquids. 2020;58(5):559–565. https://doi.org/10.1080/00319104.2019.1616194
50. Odelevskii V.I. Calculation of generalized conductivity of heterogeneous systems. Journal of Technical Physic. 1951;21(6):667–685. (In Russ.).
51. Ono Y., Hirayama K., Furukawa K. Electric resistivity of molten Fe-C, Fe-Si, and Fe-C-Si alloys. Tetsu-to-Hagane. 1974;60(14):2110–2118. https://doi.org/10.2355/tetsutohagane1955.60.14_2110
52. Kudryavtseva E.D., Singer V.V., Radovskii I.Z. Electronic structure of liquid alloys of iron with manganese, chromium and vanadium. Izvestiya vuzov. Fizika. 1983;(1):55–58. (In Russ.).
53. Chikova O.A., Tsepelev V.S., Moskovskikh O.P. Estimating the parameters of the microheterogeneous structure of metal melts according to viscometric experimental data in terms of the absolute reaction rate theory. Russian Journal of Physical Chemistry A. 2017;91(6):979–983. https://doi.org/10.7868/S0044453717060073
54. Chikova O.A., Sinitsin N.I., V’yukhin V.V. Parameters of the microheterogeneous structure of liquid 110G13L steel. Russian Journal of Physical Chemistry A. 2019;93(8): 1435–1442. https://doi.org/10.1134/S0044453719080065
55. Tyagunov G.V., Baryshev E.E., Vandysheva I.V., Zaitseva N.V., Khomenko A.O. Structure and properties of liquid iron. Bulletin of SUSU. Series “Metallurgy”. 2019;19(3): 13–23. (In Russ.).
56. Potapov M.G., Babaev A.A., Gulyaev Yu.E. Classification of complex-alloyed cast irons by the temperature of melt clusters disordering during development of TTM. Actual problems of modern science, technology and education. 2022;13(1):31–35. (In Russ.).
About the Authors
V. S. TsepelevRussian Federation
Vladimir S. Tsepelev, Dr. Sci. (Eng.), Prof., Director of the Research Center of Physics of Metallic Liquids
19 Mira Str., Yekaterinburg 620002, Russian Federation
N. I. Sinitsin
Russian Federation
Nikolai I. Sinitsin, Cand. Sci. (Phys.–Math.), Assist. Prof. of the Chair of Physics, Senior Researcher of the Research Center of Physics of Metallic Liquids
19 Mira Str., Yekaterinburg 620002, Russian Federation
O. A. Chikova
Russian Federation
Ol’ga A. Chikova, Dr. Sci. (Phys.–Math.), Prof. of the Chair of Physics
19 Mira Str., Yekaterinburg 620002, Russian Federation
M. G. Potapov
Russian Federation
Mikhail G. Potapov, Cand. Sci. (Eng.), Assist. Prof. of the Chair “Foundry Processes and Materials Science”
38 Lenina Ave., Magnitogorsk, Chelyabinsk Region 455000, Russian Federation
V. V. V’yukhin
Russian Federation
Vladimir V. V’yukhin, Senior Researcher of the Research Center of Physics of Metallic Liquids
19 Mira Str., Yekaterinburg 620002, Russian Federation
Review
For citations:
Tsepelev V.S., Sinitsin N.I., Chikova O.A., Potapov M.G., V’yukhin V.V. Microheterogeneous structure of liquid cast irons IChKh28N2 and ICh310Kh24M2F4TR. Izvestiya. Ferrous Metallurgy. 2024;67(5):579-592. https://doi.org/10.17073/0368-0797-2024-5-579-592