Scroll to:
Stress-strain state of ceramic shell mold during formation of spherical steel casting in it. Part 1
https://doi.org/10.17073/0368-0797-2024-2-211-218
Abstract
The task of the present theoretical investigation was to determine the external factors at which a spherical shell mold will not fail due to temperature stresses occurring in it. The problem is formulated for determining the stress-strain state of the spherical shell mold formed in the support filler at cooling of solidifying spherical steel casting. The investigated axisymmetric rotational body has four zones: liquid metal, solid metal, shell mold, and support filler. To solve the problem, the equation of linear elasticity, the equation of heat capacity and a well-proven numerical method were used according to which the investigated zone is partitioned into elements by a system of orthogonal surfaces. For each element, a formulated system of equations is written in difference form, taking into account axial symmetry through the values of stresses and displacements along the element edges and the lengths of the ribs’ arcs that limit its volume. The heat conduction equation is written in difference form for construction of a heat balance for an arbitrary orthogonal element, including both average temperature of the element and temperatures of the elements surrounding its volume. The authors found the solution of the difference analogue of heat equation by the “sweep” method according to the compiled iterative scheme. A difference analogue of the formulated system of differential equations of the linear theory of elasticity has the form of an algebraic system of equations. The algorithm for convolution of this system allows one to significantly reduce its rank. A general numerical scheme and algorithm for solving the problem are presented. The result of the solution is the magnitude of stresses, displacements on average along the edges of each element and average temperature in the element.
For citations:
Odinokov V.I., Evstigneev A.I., Dmitriev E.A., Namokonov A.N., Evstigneeva A.A., Chernyshova D.V. Stress-strain state of ceramic shell mold during formation of spherical steel casting in it. Part 1. Izvestiya. Ferrous Metallurgy. 2024;67(2):211-218. https://doi.org/10.17073/0368-0797-2024-2-211-218
Introduction
Numerous analytical [1; 2] and theoretical studies [3 – 5] have investigated the crack resistance of a ceramic shell mold (CSM) after liquid metal is poured into it and the solidifying casting is cooled. A glass-shaped shell mold bounded by spherical and cylindrical surfaces was studied. It was established that the most dangerous stresses that arise when liquid metal is cooled in the shell mold are normal tensile stresses on the outer surface of the mold adjacent to the support filler. The researchers determined the optimal external force and temperature influences on the shell mold to guarantee its durability during steel casting production. Additionally, they studied the morphological structures of shell molds that can withstand the thermal stresses of cooled castings and proposed new designs.
Numerous theoretical and experimental studies have been conducted to establish the characteristics of the stress-strain state (SSS) of a ceramic shell mold and the resulting castings in investment casting, and the SSS dependence on factors such as the consumable pattern [6; 7], the shape and geometry of the ceramic shell mold [8; 9], mold wall thickness [10; 11], mold material [12; 13], geometry of castings [14 – 16], and methods of mold strength tests [17; 18].
Other works describe mathematical modeling of these processes, including modeling methods [19], research methods [20 – 22], studies based on numerical modeling [23 – 25], special mathematical models [26 – 28], and software [29; 30]).
Further theoretical studies have shown that the durability of shell molds largely depends on their shape, which is organically related to the geometry of the casting formed in them.
However, practically no studies have investigated the modeling of the crack resistance of a ceramic shell mold based on the quantitative and qualitative indicators of its stress-strain state as a steel casting in the shape of a sphere (ball) is formed in it. This issue is addressed in our study.
We conducted a theoretical study related to steel casting production in a spherical shell mold. A variety of parts have spherical shapes, including spherical joints, which are crucial components in mechanical engineering and robotics.
The first theoretical results of the investigated manufacturing process were published in [31], where it was clearly shown that the stress-strain state in a spherical shell mold is drastically different from that in a cylindrical shell mold when producing a steel casting. However, the paper [31] does not present a mathematical model of the process.
This study shows that high-quality billets for spherical joints can be obtained using casting, which is much cheaper than metal treatment under pressure.
Engineering problem statement
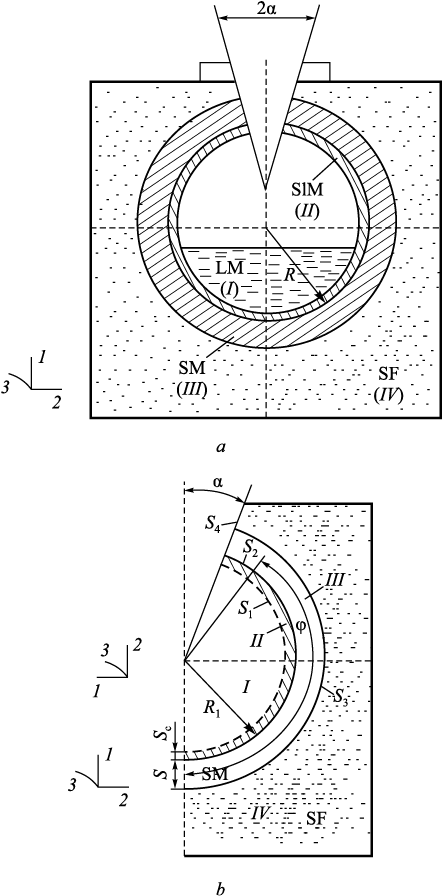
Liquid steel is poured into a spherical mold, where it crystallizes by removing heat through the shell mold walls via the support filler (Fig. 1, а). A spherical shell mold can be monolithic or consist of several layers [1], each with its own physical and mechanical properties. When steel is cooled in a shell mold, temperature stresses arise in the wall due to a large temperature gradient. Under certain external influences, these stresses can lead to wall destruction, resulting in the rejection of the steel casting. Therefore, the objective of this theoretical study is to determine the external factors under which the spherical shell mold will not be destroyed by the temperature stresses arising in it.
Fig. 1. General (a) and calculation (b) diagrams of a spherical |
Mathematical problem statement
An axisymmetric rotational body is under consideration. The deformable material is considered isotropic, and the movement is deemed slow.
We have a four-component system (Fig. 1, b). The deformable medium includes the solidified metal (region II) and the mold (region III), both of which are isotropic materials. The process is non-stationary. Using the theory of elasticity and the Eulerian reference frame, we write a system of equations for each region:
‒ for region I:
| \[\begin{array}{c}{\sigma _{11}} = {\sigma _{22}} = {\sigma _{33}} = \sigma = P;\\P = \gamma h;{\rm{ }}\theta = {\alpha _1}\Delta \theta ;\end{array}\] | (1) |
‒ for regions II, III:
| \[\left\{ \begin{array}{l}{\sigma _{ij}} = 0,i;j = 1,2,3;\\{\sigma _{ij}} - \sigma {\delta _{ij}} = 2{G_p}\varepsilon _{ij}^*;{\rm{ }}\varepsilon _{_{ij}}^* = {\varepsilon _{ij}} - \frac{1}{3}\varepsilon {\delta _{_{ij}}};{\rm{ }}\varepsilon = {\varepsilon _{ii}};\\{\varepsilon _{ii}} = 3{k_p}\sigma + 3{\alpha _p}(\theta - \theta _p^*);{\rm{ }}{\varepsilon _{ij}} = 0,5({U_{ij}} + {U_{ji}});\\{C_p}\gamma \frac{{\partial \theta }}{{\partial \tau }} = {\rm{div}}(\lambda {\rm{grad}}\theta );\end{array} \right.\] | (2) |
where σij are the components of the stress tensor; σ is the hydrostatic stress; εij are the components of the elastic strain tensor; h is the height of the liquid metal column; \({k_p} = \frac{{1 - 2\mu }}{E}\) is the coefficient of volume compressibility; μ is Poisson’s ratio; E is Young’s modulus; Gp is the shear modulus in region p (II, III); αp is the linear expansion coefficient; a1 is the temperature conductivity coefficient in the region I; τ is time; θ is temperature; Cp is the specific heat in the region p; γ is density; \(\theta _p^*\) is the initial temperature in the region p; λ = λ(θ) is heat conduction; \({\sigma _{ij,j}} = \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}};{\rm{ }}{u_{i,j}} = \frac{{\partial {u_i}}}{{\partial {x_j}}};\) and summation over repeated indices is performed.
In accordance with axial symmetry, we consider the meridian section (Fig. 1, b).
If θm ≤ θcr (θm and θcr are the temperatures of the metal and crystallization), as the liquid metal is cooled, its temperature is determined by the thickness of the solidified layer Δi from the solution of the interphase transition equation [5].
Initial statement of the problem:
Δ|τ = 0 = 0 (absence of the metal solid phase);
\(\theta _I^*\)|τ = 0 = 0 = \(\theta _{\rm{м}}^*\) (temperature of the poured liquid metal);
\(\theta _{III}^*\)|τ = 0 = θ\(^*\) (initial mold temperature).
Boundary conditions of the problem (Fig. 1, b):
‒ on the axis of symmetry: U2 = 0; σ21 = 0; qn = 0;
‒ on surfaces S1 , S3 , S4
| \[\begin{array}{c}{\sigma _{11}}{|_{{S_1}}} = - P;{\rm{ }}{\sigma _{12}}{|_{{S_1}}} = 0;{\rm{ }}{U_1}{|_{{S_3}}} = 0;{\rm{ }}{\sigma _{22}}{|_{{S_4}}} = 0;\\{\sigma _{12}}{|_{{S_3}}} = - \psi \frac{{{U_{ck}}}}{{{U^*}}}con({n_1}{x_1});{\rm{ }}\theta {|_{{S_3}}} = {\theta ^*};\end{array}\] | (3) |
where Uck is the sliding of the mold material relative to the sand; \(U^*\) is the normalizing displacement; and ψ is a parameter characterizing the friction conditions between the mold and the support filler.
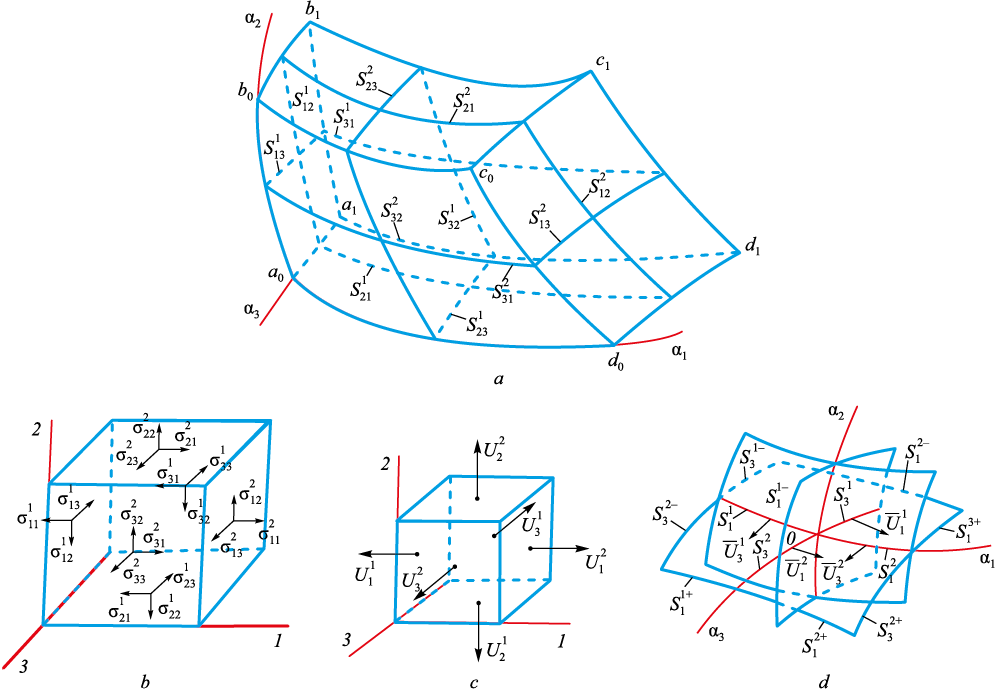
The numerical method was used [32] to solve the system (2). According to this method, the deformation region is divided into a finite number of orthogonal curved elements (Fig. 2, а).
Fig. 2. Deformation zone: |
With axial symmetry, we have σ31 = σ32 = 0; σ13 = σ23 = 0; U3 = 0.
In accordance with [32], the equations (2) and the values εii taking into account axial symmetry, will be written as follows:
| \[\begin{array}{c}{S_{13}}\Delta {S_{12}}({\sigma _{11}} - {\sigma _{22}}) + {S_{12}}{S_{13}}({\sigma _{11}} - {\sigma _{33}}) + \\ + 0,5\Delta {\sigma _{11}}{S_{12}}{S_{13}} + 0,5\Delta {\sigma _{12}}{S_{21}}{S_{23}} + \\ + ({S_{21}}\Delta {S_{23}} + 2{S_{23}}\Delta {S_{21}}){\sigma _{21}} = 0;\\{S_{21}}\Delta {S_{23}}({\sigma _{22}} - {\sigma _{33}}) + {S_{23}}{S_{21}}({\sigma _{22}} - {\sigma _{11}}) + \\ + 0,5\Delta {\sigma _{22}}{S_{23}}{S_{21}} + 0,5\Delta {\sigma _{21}}{S_{12}}{S_{13}} + \\ + ({S_{12}}\Delta {S_{13}} + 2{S_{13}}\Delta {S_{12}}){\sigma _{21}} = 0;\end{array}\] | (4) |
| \[\begin{array}{c}{\sigma _{11}} - {\sigma _{22}} = 2{G_p}({\varepsilon _{11}} - {\varepsilon _{22}});\\{\sigma _{22}} - {\sigma _{33}} = 2{G_p}({\varepsilon _{22}} - {\varepsilon _{33}});\end{array}\] | (5) |
| \[{\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _{33}} = 3{k_p}\sigma + 3{\alpha _p}(\theta - \theta _p^*);\] | (6) |
| \[\begin{array}{c}{\varepsilon _{11}} = \frac{{2\Delta {U_1}}}{{{S_{21}}}} + \frac{{2{U_2}}}{{{S_{21}}}}\frac{{\Delta {S_{21}}}}{{{S_{12}}}};\\{\varepsilon _{22}} = \frac{{2\Delta {U_2}}}{{{S_{32}}}} + \frac{{2{U_1}}}{{{S_{12}}}}\frac{{\Delta {S_{12}}}}{{{S_{21}}}};\\{\varepsilon _{33}} = \frac{{2{U_1}}}{{{S_{13}}}}\frac{{\Delta {S_{13}}}}{{{S_{31}}}} + \frac{{2{U_2}}}{{{S_{23}}}}\frac{{\Delta {S_{23}}}}{{{S_{32}}}};\end{array}\] | (7) |
where \({U_i} = U_i^1 + U_i^2,{\rm{ }}\Delta {U_i} = U_i^2 - U_i^1,\) (i = 1, 2); \({S_{ij}} = S_{ij}^1 + S_{ij}^2;{\rm{ }}\Delta {S_{ij}} = S_{ij}^2 - S_{ij}^1.\)
The adopted symbols are described in [1; 7].
The equations (4) – (7) are written taking into account that \(\frac{{\partial {U_1}}}{{\partial {x_3}}} = 0,{\rm{ }}\frac{{\partial {\sigma _{3i}}}}{{\partial {x_3}}} = 0;\) i = 1, 2, 3; for rotational bodies ΔS31 = 0; ΔS32 = 0; \(\frac{{\Delta {U_1}}}{{{S_3}}} = 0;{\rm{ }}\frac{{\Delta {U_2}}}{{{S_3}}} = 0;\) U3 = 0; on the surface x1x3 : \(S_2^ + - S_2^ - = 0;\) on the surface x2x3 : \(S_2^ + - S_2^ - = 0;\) shift values εij (i ≠ j) shall be written for the node (0) (Fig. 2, d) in the form
| \[\begin{array}{c}\varepsilon _{12}^0 = \frac{{2\Delta {{\bar U}_2}}}{{{S_1}}} - 0,5{{\bar U}_2}\frac{{S_2^ + - S_2^ - }}{{{S_1}{S_2}}} + \\ + \frac{{2\Delta {{\bar U}_1}}}{{{S_2}}} - 0,5{{\bar U}_1}\frac{{S_1^ + - S_1^ - }}{{{S_1}{S_2}}},\end{array}\] | (8) |
where \({S_i} = S_i^1 + S_i^2;{\rm{ }}\Delta {\bar U_l} = {\bar U_{{l_2}}} - {\bar U_{{l_1}}};{\rm{ }}S_i^ + = S_i^{1 + } + S_i^{2 + };\) \(S_i^ - = S_i^{1 - } + S_i^{2 - };\) \({\bar U_l}\) is the average of the value Ui along the element edges.
The authors of [32] prove that if there are initial and boundary conditions, the difference analogue of the system (4) – (6), taking into account the equation (7), is definable. The order of the system (4) – (6) is significantly reduced when the following operations are performed.
1. The differences (σij – σjj) in equations (4) are expressed by formula (5).
2. The mass conservation equation is rewritten in the recurrent form, taking into account expressions (7), in the form \(U_1^2\) = \(U_1^1\) + [A]; where [A] is an operator that does not contain \(U_1^2\); direction of bypassing the area along x1 (→), along x2 (↑).
3. Shift expressions εij (i ≠ j) are determined based on internal grid nodes in accordance with formulas (8); i = 1, j = 2.
4. The values σij (i ≠ j) are determined based on the internal grid nodes from the equations of state \(\sigma _{12}^0 = G_p^0\varepsilon _{12}^0.\)
5. The values σij are determined based on the external grid nodes from the boundary conditions, and on the contact surfaces – from the friction law.
6. σij are determined based on the element edges as the average of the values σij at the edges’ nodes.
7. The first equation (4) is rewritten in the recurrent form \(\sigma _{11}^1\) = \(\sigma _{11}^2\) + [Б]; where [Б] is an operator that does not contain \(\sigma _{11}^1\); direction of bypassing the area along x1 (←), along x2 (↓).
8. From the system of equations (the second equation in the system (4) and the equation σ22 – σ11 = 2λ(ε11 – ε22)) the values \(\sigma _{22}^1\) and \(\sigma _{22}^2\) for the element are determined, the equations of the form \({F_3} = {(\sigma _{22}^2)_{IJ}} - {(\sigma _{22}^1)_{IJ + 1}} = 0\) composed for the internal edges (where J is the element index on the coordinate x2 ).
Thus, if we consider \(X = \left\{ {{U_2},} \right.{\left. {{\rm{ }}{U_1}} \right|_{{x_1} = 0}},{\left. {{\rm{ }}{\sigma _{11}}} \right|_{{x_1}}} = \left. {x_1^*} \right\},\) independent variables, the sequence (1) ‒ (7) can be used to determine the dependent variables through X (\(x_1^*\) is the final value of the coordinate x in the curved region.
The equivalent system of equations looks as follows
| \[\begin{array}{c}{F_1} = (U_1^2 - U_1^*{\left. ) \right|_{{x_1} = x_1^*}} = 0;\\{F_2} = (\sigma _{11}^1 - \sigma _{11}^*{\left. ) \right|_{{x_1} = 0}} = 0;{\rm{ }}\\{F_3} = 0;\end{array}\] | (9) |
where \(U_1^*\)is known from the boundary conditions of displacement U1 at the boundary of the region (x1 = \(x_1^*\)); \(\sigma _{11}^*\) is known from the boundary conditions of stress σ11 at the boundary of the region (x1 = 0).
There are as many equations F1 = 0 as there are unknown variables \({\left. {{\sigma _{11}}} \right|_{{x_1} = x_1^*}},\) and as many equations F2 = 0 as there are unknown variables \({\left. {{U_1}} \right|_{{x_1}}}\) = 0.
The coefficients and free terms of the new equivalent system of equations (9) can be found using the following procedure.
Suppose the equivalent system of equations looks as follows
| \[{\bar F_i} = {\alpha _{ij}}{x_j} + {b_i} = 0;{\rm{ }}i,{\rm{ }}j = 1,{\rm{ }}...,{\rm{ }}n.\] | (10) |
If we assume that all unknown variables are equal to zero (xi = 0, i = 1, ..., n), based on the above sequence (1) – (7) and the calculation of \({\bar F_i}\) by the formulas (9), we will find the free terms of the new system (10):
\[{\bar F_i}^0 = {b_i};{\rm{ }}i = 1,{\rm{ }}...,{\rm{ }}n.\]
Next, we find the coefficients aij . To do so, we calculate xk = 1, xi = 0 (i ≠ k; i = 1, ..., n). Using the above sequence, we find the value \(\bar F_i^k\) and aik by the following formula:
\[{a_{ik}} = F_i^k - F_i^0,{\rm{ }}i = 1,{\rm{ }}...,{\rm{ }}n.\]
Thus, we determine the entire matrix aik of the new equivalent system, which is solved using a standard program. The order of the equivalent system is reduced by approximately 10 times compared to the original one.
The heat conduction equation is solved using a numerical method [1; 32]. Under the method being considered, for each internal k\(^\rm{th}\) element (Fig. 2, а) the heat conduction system is written from the heat balance in difference form, taking into account axial symmetry, and an iterative procedure is constructed, which, given that the heat flow along x3 is equal to zero, is represented by the iterative formula:
| \[\begin{array}{c}{\theta _k} = \frac{{\theta _k^* + {t_{12}}\theta _1^ + + {t_{11}}\theta _1^ - + {t_{22}}\theta _2^ + + {t_{21}}\theta _2^ - }}{{1 + {t_{12}} + {t_{11}} + {t_{22}} + {t_{21}}}};\\{t_{12}} = \frac{{2({\lambda _k} + \lambda _1^ + )}}{{{S_{21}} + S_{21}^ + }}F_1^2\frac{{\Delta \tau }}{{{C_k}{\gamma _k}{V_k}}};\\{t_{11}} = \frac{{2({\lambda _k} + \lambda _1^ - )}}{{{S_{21}} + S_{21}^ + }}F_1^1\frac{{\Delta \tau }}{{{C_k}{\gamma _k}{V_k}}};\\{t_{22}} = \frac{{2({\lambda _k} + \lambda _2^ + )}}{{{S_{12}} + S_{12}^ + }}F_2^2\frac{{\Delta \tau }}{{{C_k}{\gamma _k}{V_k}}};\\{t_{21}} = \frac{{2({\lambda _k} + \lambda _2^ - )}}{{{S_{12}} + S_{12}^ - }}F_2^1\frac{{\Delta \tau }}{{{C_k}{\gamma _k}{V_k}}};\\F_i^j = S_{ik}^jS_{ip}^j;{\rm{ }}i \ne k \ne p;{\rm{ }}i,{\rm{ }}k,{\rm{ }}p = 1,2,3;{\rm{ }}j = 1,{\rm{ }}2;\\{V_k} = \frac{{{S_{13}}{S_{12}}({S_{21}} + {S_{31}})}}{{16}};\end{array}\] | (11) |
where \(\theta _k^*\)is the average temperature in the k\(^\rm{th}\) element at the beginning of the time step Δτ; λk , θk , Ck , γk are the average heat conduction, temperature, heat capacity, and density in the k\(^\rm{th}\) element at the end of the time step Δτ; \(\lambda _i^ - ,{\rm{ }}\theta _i^ - \) and \(\lambda _i^ + ,{\rm{ }}\theta _i^ + \), (i = 1, 2) are the heat conduction and temperature in the element following the element k on the coordinate xi in the negative and positive directions xi ; \(S_{21}^ - = S_{21}^{1 - } + S_{21}^{2 - };\) \(S_{21}^ + = S_{21}^{1 + } + S_{22}^{2 + };\) \(S_{ij}^{1 + }\) (i ≠ j; i, j = 1, 2) and \(S_{ij}^{1 - }\) are the length of the arc \(S_{ij}^1\)of the element following the element k in the positive and negative directions on the coordinate xj .
The authors of [32] proved the iteration procedure convergence (11).
Algorithm for solving the problem
1. The cooling time τ\(^*\) is divided into a finite number of steps: \({\tau ^*} = \sum {\Delta {\tau _n}} ;\) where n is the number of the time step.
2. The region under study is divided into a finite number of orthogonal elements.
3. The initial and boundary conditions for the elements forming the investigated region and the constants of the physical and mechanical properties of the materials are established.
4. The lengths of the elements’ arcs are calculated \(S_{ik}^j\) (i, k = 1, 2; i ≠ k; j = 1, 2).
5. The temperature field at the time step Δτn is determined by the numerical solution of the heat equation using the iterative formula (11) if there are initial and boundary conditions at the investigated time step.
6. If the temperature in the region I near the surface S2 \({\left. \theta \right|_{{S_2}}} \le {\theta _k},\) the thickness Δn of the crystallized crust is calculated [5]. If \({\left. \theta \right|_{{S_2}}} > {\theta _k},\) the following operation is performed.
7. The system of equations (2) is solved taking into account difference analogues (4) – (7) and the developed procedures [1; 32] described above. The fields of stress σij and displacements Ui (i, j = 1, 2) are determined.
8. Time steps are taken; if \(\sum {\Delta {\tau _n}} < {\tau ^*},\) the operation 4 is performed; if \(\sum {\Delta {\tau _n}} = {\tau ^*}\) he calculation process is completed.
As the temperature problem was solved, boundary conditions of the first kind (3) were used. To determine θm(τ) and θ\(^*\)(τ) we will use the experimental data from [1]. Approximation of these values yields the following result:
\[\begin{array}{c}{\theta _{\rm{м}}} = 1550 - 1.666\tau - \frac{{\tau (60 - \tau )}}{{10 + {\tau ^2}}};\\\theta \le \tau \le 60{\rm{ s}};\\{\theta ^*} = 20 + 17.3\sqrt \tau ;\end{array}\]
where τ is the cooling time, s.
The time τ does not exceed 60 s, since at τ ≥ 60 s the stresses in the shell mold plummet and cannot cause its destruction.
A mathematical model has been developed to determine the stress-strain state and temperature in the shell mold when a spherical casting is cooled in it. This model was used in a numerical solution of the problem on modeling the crack resistance of a spherical shell mold.
Conclusions
The first theoretical attempt was made to formulate and solve the problem of determining external factors at which a spherical shell mold will not fail due to temperature stresses occurring in it.
Based on the fundamental equations of the theory of elasticity and numerical methods, a numerical scheme and algorithm for solving the problem were developed.
The proposed method for modeling the crack resistance of a spherical shell can be recommended for other functional shells.
References
1. Odinokov V.I., Dmitriev E.A., Evstigneev A.I., Sviridov A.V. Mathematical Modeling of the Processes of Obtaining Castings in Ceramic Shell Molds. Moscow: Innovatsionnoe mashinostroenie; 2020:224. (In Russ.).
2. Evstigneev A.I., Odinokov V.I., Dmitriev E.A., Sviridov A.V., Ivankova E.P. The influence of external heat exposure on the stress state of shell forms by smelting models. Matematicheskoe modelirovanie. 2021;33(1):63–76. (In Russ.). https://doi.org/10.20948/mm-2021-01-05
3. Odinokov V.I., Dmitriev E.A., Evstigneev A.I., Sviridov A.V., Ivankova E.P. Choice of materials properties and of shell molds structure by investment models. Izvestiya. Ferrous Metallurgy. 2020;63(9):742–754. (In Russ.). https://doi.org/10.17073/0368-0797-2020-9-742-754
4. Odinokov V.I., Evstigneev A.I., Dmitriev E.A., Chernyshova D.V., Evstigneeva A.A. Influence of support filler and structure of shell mold on its crack resistance. Izvestiya. Ferrous Metallurgy. 2022;65(4):285–293. (In Russ.). https://doi.org/10.17073/0368-0797-2022-4-285-293
5. Evstigneev A.I., Dmitriev E.A., Chernysheva D.V., Odinokov V.I., Evstigneeva A.A., Ivankova E.P. Modeling of external force action on a shell mold for pouring steel. Matematicheskoe modelirovanie. 2022;34(5):61–72. (In Russ.). https://doi.org/10.20948/mm-2022-05-04
6. Bansode S.N., Phalle V.M., Mantha S.S. Optimization of process parameters to improve dimensional accuracy of investment casting using Taguchi approach. Advances in Mechanical Engineering. 2019;11(4):1–12. https://doi.org/10.1177/1687814019841460
7. Mittal Y.G., Kamble P., Gote G., Patil Y., Patel A. K., Bernard A., Karunakaran K.P. Mathematical modelling of pattern sublimation in rapid ice investment casting. International Journal of Metalcasting. 2022;16(2):1002–1009. http://dx.doi.org/10.1007/s40962-021-00665-w
8. Kanyo J.E., Schafföner S., Uwanyuze R.S., Leary K.S. An overview of ceramic molds for investment casting of nickel superalloys. Journal of the European Ceramic Society. 2020;40(15):4955–4973. https://doi.org/10.1016/j.jeurceramsoc.2020.07.013
9. Rafique M.M.A., Iqbal J. Modeling and simulation of heat transfer phenomena during investment casting. International Journal of Heat and Mass Transfer. 2009; 52(7–8):2132–2139. http://doi.org/10.1016/j.ijheatmasstransfer.2008.11.007
10. Singh R. Mathematical modeling for surface hardness in investment casting applications. Journal of Mechanical Science and Technology. 2012;26:3625–3629. http://dx.doi.org/10.1007/s12206-012-0854-0
11. Jafari H., Idris M. H., Ourdjini A. Effect of thickness and permeability of ceramic shell mould on in situ melted AZ91D investment casting. Applied Mechanics and Materials. 2014;465–466:1087–1092. http://dx.doi.org/10.4028/www.scientific.net/AMM.465-466.1087
12. Bansode S.N., Phalle V.M., Mantha S. Taguchi approach for optimization of parameters that reduce dimensional variation in investment casting. Archives of Foundry Engineering. 2019;19(1):5–12. https://dx.doi.org/10.24425/afe.2018.125183
13. Pattnaik S., Karunakar D.B., Jha P.K. Developments in investment casting process ‒ A review. Journal of Materials Processing Technology. 2012;212(11):2332–2348. https://doi.org/10.1016/j.jmatprotec.2012.06.003
14. Zhang J., Li K.W., Ye H.W., Zhang D.Q., Wu P.W. Numerical simulation of solidification process for impeller investment casting. Applied Mechanics and Materials. 2011; 80–81:961–964. https://doi.org/10.4028/www.scientific.net/AMM.80-81.961
15. Dong Y.W., Li X.L., Zhao Q., Jun Y., Dao M. Modeling of shrinkage during investment casting of thin walled hollow turbine blades. Journal of Materials Processing Technology. 2017;244:190–203. https://doi.org/10.1016/j.jmatprotec.2017.01.005
16. Rakoczy Ł., Cygan R. Analysis of temperature distribution in shell mould during thinwall superalloy casting and its effect on the resultant microstructure. Archives of Civil and Mechanical Engineering. 2018;18(4):1441–1450. https://doi.org/10.1016/j.acme.2018.05.008
17. Yameng W., Zhigang L. The design of testing methods for strength of ceramic shell mold in investment casting. Proceedings of the Asia-Pacific Conf. on Intelligent Medical 2018 & Int. Conf. on Transportation and Traffic Engineering. 2018;336–341. https://doi.org/10.1145/3321619.3321686
18. Kolczyk J., Zych J. High temperature strength of ceramic moulds applied in the investment casting method. Archives of Foundry Engineering. 2011;11(3):121–124.
19. Anglada E., Meléndez A., Maestro L., Domínguez I. Finite element model correlation of an investment casting process. Materials Science Forum. 2014;797:105–110. http://dx.doi.org/10.4028/www.scientific.net/MSF.797.105
20. Liu C., Sun J., Lai X., He B., Li F. Influence of complex structure on the shrinkage of part in investment casting process. The International Journal of Advanced Manufacturing Technology. 2015;77:1191–1203. https://doi.org/10.1007/s00170-014-6523-y
21. Liu C., Wang F., Jin S., Li F., Lai X. Permafrost analysis methodology (PAM) for ceramic shell deformation in the firing process. International Journal of Metalcasting. 2019;13(4):953–968. http://dx.doi.org/10.1007/s40962-019-00317-0
22. Everhart W.A., Lekakh S.N., Richards V., Chen J., Li H., Chandrashekhara K. Corner strength of investment casting shells. International Journal of Metalcasting. 2013;7:21–27. https://doi.org/10.1007/BF03355541
23. Sabau A.S. Numerical simulation of the investment casting process. Transactions of American Foundry Society. 2005;113:407–417.
24. Zheng K., Lin Y., Chen W., Liu L. Numerical simulation and optimization of casting process of copper alloy water-meter shell. Advances in Mechanical Engineering. 2020;12(5): 1–12. http://dx.doi.org/10.1177/1687814020923450
25. Manzari M.T., Gethin D.T., Lewis R.W. Optimisation of heat transfer between casting and mould. International Journal of Cast Metals Research. 2000;13(4):199–206. https://doi.org/10.1080/13640461.2000.11819402
26. Rafique M.M.A., Shah U. Modeling and simulation of heat transfer phenomenon related to mold heating during investment casting. Engineering. 2020;12(5):291–314. http://dx.doi.org/10.4236/eng.2020.125024
27. Dong Y., Bu K., Zhang D. Numerical simulation of displacement field of solidification process for investment casting. In: 2008 Asia Simulation Conf. – 7th Int. Conf. on System Simulation and Scientific Computing. 2008:715–720. https://doi.org/10.1109/asc-icsc.2008.4675453
28. Upadhya G.K., Das S., Chandra U., Paul A.J. Modelling the investment casting process: a novel approach for view factor calculations and defect prediction. Applied Mathematical Modelling.1995;19(6):354–362. https://doi.org/10.1016/0307-904X(95)90001-O
29. Khan M.A.A., Sheikh A.K. Simulation tools in enhancing metal casting productivity and quality: A review. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture. 2016;230(10):1799–1817. https://doi.org/10.1177/0954405416640183
30. Banerjee S., Sutradhar G. Analysis of casting defects in investment casting by simulation. Advances in Materials, Mechanical and Industrial Engineering: Selected Contributions from the First Int. Conf. on Mechanical Engineering, Jadavpur University, Kolkata, India. Springer International Publishing. 2019:247–271. http://dx.doi.org/10.1007/978-3-319-96968-8_12
31. Evstigneev A.I., Odinokov V.I., Dmitriev E.A., Chernyshоva D.V., Evstigneeva A.A., Ivankova E.P. On the crack resistance of a ceramic shell mold according to smelted models when a spherical steel casting solidifies in it. Liteinoe proizvodstvo. 2022;(9):17–21. (In Russ.).
32. Odinokov V.I., Kaplunov B.G., Peskov A.V., Bakov A.V. Mathematical Modeling of Complex Technological Processes. Moscow: Nauka; 2008:178. (In Russ.).
33.
About the Authors
V. I. OdinokovRussian Federation
Valerii I. Odinokov, Dr. Sci. (Eng.), Prof., Chief Researcher of the Department of Research Activities
27 Lenina Ave., Khabarovsk Territory, Komsomolsk-on-Amur 681013, Russian Federation
A. I. Evstigneev
Russian Federation
Aleksei I. Evstigneev, Dr. Sci. (Eng.), Prof., Chief Researcher of the Department of Research Activities
27 Lenina Ave., Khabarovsk Territory, Komsomolsk-on-Amur 681013, Russian Federation
E. A. Dmitriev
Russian Federation
Eduard A. Dmitriev, Dr. Sci. (Eng.), Assist. Prof., Rector
27 Lenina Ave., Khabarovsk Territory, Komsomolsk-on-Amur 681013, Russian Federation
A. N. Namokonov
Russian Federation
Aleksandr N. Namokonov, Postgraduate
27 Lenina Ave., Khabarovsk Territory, Komsomolsk-on-Amur 681013, Russian Federation
A. A. Evstigneeva
Russian Federation
Anna A. Evstigneeva, Student of the Chair “Applied Mathematics”
27 Lenina Ave., Khabarovsk Territory, Komsomolsk-on-Amur 681013, Russian Federation
D. V. Chernyshova
Russian Federation
Dar’ya V. Chernyshova, Postgraduate of the Chair of Aircraft Engineering
27 Lenina Ave., Khabarovsk Territory, Komsomolsk-on-Amur 681013, Russian Federation
Review
For citations:
Odinokov V.I., Evstigneev A.I., Dmitriev E.A., Namokonov A.N., Evstigneeva A.A., Chernyshova D.V. Stress-strain state of ceramic shell mold during formation of spherical steel casting in it. Part 1. Izvestiya. Ferrous Metallurgy. 2024;67(2):211-218. https://doi.org/10.17073/0368-0797-2024-2-211-218