Перейти к:
Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 1
https://doi.org/10.17073/0368-0797-2024-2-211-218
Аннотация
Задачей настоящего теоретического исследования является определение внешних факторов, при которых сферическая оболочковая форма (ОФ) не будет разрушаться от возникающих в ней температурных напряжений. Сформулирована задача по определению напряженно-деформируемого состояния (НДС) ОФ, заформированной в опорный наполнитель (ОН), при охлаждении в ней затвердевающей шарообразной стальной отливки. Рассматриваемое осесимметричное тело вращения имеет четыре области (жидкий металл, твердый металл, оболочковая форма, опорный наполнитель). Для решения задачи авторы используют уравнение линейной теории упругости, уравнение теплопроводности и апробированный численный метод, согласно которому исследуемая область разбивается системой ортогональных поверхностей на элементы. Для каждого элемента записана система уравнений в разностном виде с учетом осевой симметрии через напряжения и перемещения по граням элемента и длинам дуг ребер, ограничивающих его объем. Уравнение теплопроводности записано в разностном виде из построения теплового баланса для произвольного ортогонального элемента, включающее как среднюю температуру элемента, так и температуры элементов, окружающих его объем. Решение разностного аналога уравнения теплопроводности осуществляется методом «прогонки» по составленной итерационной схеме. Приведен разностный аналог сформулированной системы дифференциальных уравнений линейной теории упругости в виде алгебраической системы уравнений. Представленный алгоритм свертки этой системы позволяет значительно понизить ее ранг.. Приводится общая численная схема и алгоритм решения задачи. Результатом решения являются величины напряжений, перемещений в среднем по граням каждого элемента и средняя температура в элементе.
Ключевые слова
Для цитирования:
Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Намоконов А.Н., Евстигнеева А.А., Чернышова Д.В. Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 1. Известия высших учебных заведений. Черная Металлургия. 2024;67(2):211-218. https://doi.org/10.17073/0368-0797-2024-2-211-218
For citation:
Odinokov V.I., Evstigneev A.I., Dmitriev E.A., Namokonov A.N., Evstigneeva A.A., Chernyshova D.V. Stress-strain state of ceramic shell mold during formation of spherical steel casting in it. Part 1. Izvestiya. Ferrous Metallurgy. 2024;67(2):211-218. https://doi.org/10.17073/0368-0797-2024-2-211-218
Введение
Проведены аналитические [1; 2] и теоретические исследования [3 ‒ 5] по трещиностойкости керамической оболочковой формы (КОФ) после заливки в нее жидкого металла и охлаждения затвердевающей отливки. Исследовалась оболочковая форма (ОФ) в форме стакана, ограниченная сферической и цилиндрической поверхностями. Установлено, что наиболее опасным напряжением, возникающим при охлаждении в ОФ жидкого металла, являются растягивающие нормальные напряжения на наружной поверхности формы, примыкающей к опорному наполнителю (ОН). Найдены оптимальные внешние силовые и температурные воздействия на ОФ, гарантирующие ее стойкость при получении в ней стальной отливки. Кроме того, изучены и предложены новые морфологические структуры ОФ, выдерживающие термические напряжения охлаждающихся в них отливок.
Проведено множество теоретических и экспериментальных исследований по установлению особенностей напряженно-деформированного состояния (НДС) керамической оболочковой формы и получаемых отливок в литье по выплавляемым моделям (ЛВМ) по влиянию на НДС материалов выплавляемых моделей [6; 7], формы и геометрии КОФ [8; 9], толщины стенки формы [10; 11], материала формы [12; 13], геометрии отливок [14 ‒ 16], методов испытаний формы на прочность и пр. [17; 18].
Математическое моделирование таких процессов также представлено в других работах (в частности, методы моделирования [19], методы исследований [20 ‒ 22], исследования с использованием численного моделирования [23 ‒ 25], специальных математических моделей [26 ‒ 28] и программных средств [29; 30]).
Как показали дальнейшие теоретические исследования, на стойкость ОФ большое влияние оказывает их форма, органически связанная с геометрией формирующейся в ней отливки.
Однако работ, в которых рассматриваются процессы моделирования трещиностойкости КОФ в зависимости от количественных и качественных показателей ее НДС при формировании в ней стальной отливки в виде сферы (шара), практически нет. Именно этому процессу посвящена настоящая работа.
Приведено теоретическое исследование получения стальной отливки в ОФ в виде шара. В технике наблюдается огромное многообразие номенклатуры деталей, изготавливаемых в виде шаровой и сферической форм. К ним относятся, в первую очередь, шаровые опоры, которые являются основными узлами в машиностроении и робототехнике.
Первые теоретические результаты рассматриваемого технологического процесса опубликованы в работе [31], где наглядно показано, что НДС в ОФ коренным образом отличается от НДС в цилиндрической ОФ при получении стальной отливки. Однако в работе [31] не рассмотрена математическая модель процесса.
В настоящей работе показано, что качественные заготовки под шаровые опоры можно получать с помощью литья, что намного дешевле, чем обработкой металлов давлением.
Инженерная постановка задачи
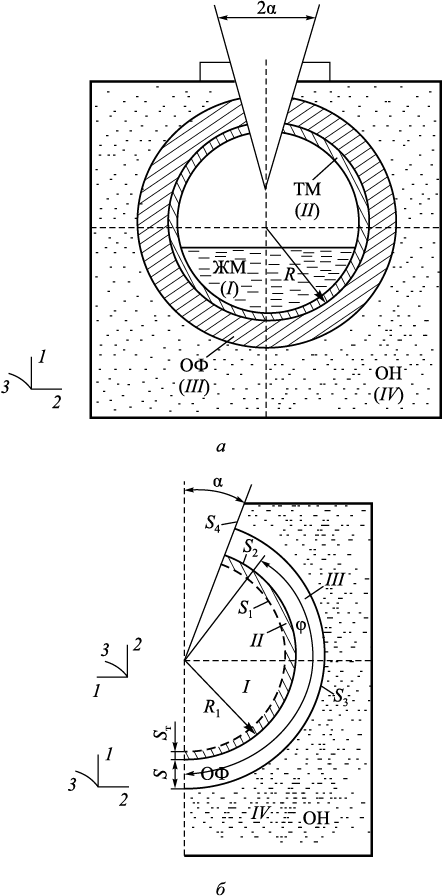
Жидкая сталь разливается в сферическую форму, в которой кристаллизуется путем отвода тепла от стенок ОФ через ОН (рис. 1, а). Сферическая ОФ может быть монолитной или состоять из ряда слоев [1]. При этом каждый слой ОФ может иметь свои физико-механические характеристики. При охлаждении стали в ОФ, вследствие большого температурного градиента, в стенке возникают температурные напряжения, которые при определенных внешних воздействиях могут привести к ее разрушению, а значит, и к браку получаемой стальной отливки. Таким образом, задачей настоящего теоретического исследования является определение внешних факторов, при которых сферическая ОФ не будет разрушаться от возникающих в ней температурных напряжений.
Рис. 1. Общая (а) и расчетная (б) схемы шарообразной ОФ, |
Математическая постановка задачи
Рассматривается осесимметричное тело вращения. Деформируемый материал считается изотропным. Движение принимали медленным.
Имеем четырехкомпонентную систему (рис. 1, б). Деформируемой средой является затвердевший металл (область II) и форма (область III) – изотропные материалы. Процесс нестационарный. Используя теорию упругости и Эйлерову систему координат, запишем для каждой из областей систему уравнений:
‒ для области I:
| \[\begin{array}{c}{\sigma _{11}} = {\sigma _{22}} = {\sigma _{33}} = \sigma = P;\\P = \gamma h;{\rm{ }}\theta = {\alpha _1}\Delta \theta ;\end{array}\] | (1) |
‒ для областей II, III:
| \[\left\{ \begin{array}{l}{\sigma _{ij}} = 0,i;j = 1,2,3;\\{\sigma _{ij}} - \sigma {\delta _{ij}} = 2{G_p}\varepsilon _{ij}^*;{\rm{ }}\varepsilon _{_{ij}}^* = {\varepsilon _{ij}} - \frac{1}{3}\varepsilon {\delta _{_{ij}}};{\rm{ }}\varepsilon = {\varepsilon _{ii}};\\{\varepsilon _{ii}} = 3{k_p}\sigma + 3{\alpha _p}(\theta - \theta _p^*);{\rm{ }}{\varepsilon _{ij}} = 0,5({U_{ij}} + {U_{ji}});\\{C_p}\gamma \frac{{\partial \theta }}{{\partial \tau }} = {\rm{div}}(\lambda {\rm{grad}}\theta );\end{array} \right.\] | (2) |
здесь σij – компоненты тензора напряжений; σ – гидростатическое напряжение; εij – компоненты тензора упругих деформаций; h – высота столба жидкого металла; \({k_p} = \frac{{1 - 2\mu }}{E}\) ‒ коэффициент объемного сжатия; μ ‒ коэффициент Пуаcсона; E – модуль Юнга; Gp – модуль сдвига в среде области p (II, III); αp – коэффициент линейного расширения; a1 – коэффициент температуропроводности в области I; τ – время; θ – температура; Cp – удельная теплоемкость в области p; γ – плотность; \(\theta _p^*\) – начальная температура в области p; λ = λ(θ) – теплопроводность; \({\sigma _{ij,j}} = \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}};{\rm{ }}{u_{i,j}} = \frac{{\partial {u_i}}}{{\partial {x_j}}};\) используется суммирование по повторяющимся индексам.
В соответствии с осевой симметрией рассмотрим меридианное сечение (рис. 1, б).
При условии θм ≤ θк (θм и θк – температуры металла и кристаллизации) в процессе охлаждения жидкого металла его температура определяется толщиной затвердевшего слоя Δi из решения уравнения межфазового перехода [5].
Начальные условия задачи:
Δ|τ = 0 = 0 – отсутствие твердой фазы металла;
\(\theta _I^*\)|τ = 0 = 0 = \(\theta _{\rm{м}}^*\) – температура разливаемого жидкого металла;
\(\theta _{III}^*\)|τ = 0 = θ\(^*\) – начальная температура формы.
Граничные условия задачи (рис. 1, б):
‒ на оси симметрии: U2 = 0; σ21 = 0; qn = 0;
‒ на поверхностях S1 , S3 , S4
| \[\begin{array}{c}{\sigma _{11}}{|_{{S_1}}} = - P;{\rm{ }}{\sigma _{12}}{|_{{S_1}}} = 0;{\rm{ }}{U_1}{|_{{S_3}}} = 0;{\rm{ }}{\sigma _{22}}{|_{{S_4}}} = 0;\\{\sigma _{12}}{|_{{S_3}}} = - \psi \frac{{{U_{ck}}}}{{{U^*}}}con({n_1}{x_1});{\rm{ }}\theta {|_{{S_3}}} = {\theta ^*};\end{array}\] | (3) |
здесь Uck – скольжение материала формы относительно песка; \(U^*\) – нормирующее перемещение; ψ – параметр, характеризующий условия трения между формой и опорным наполнителем.
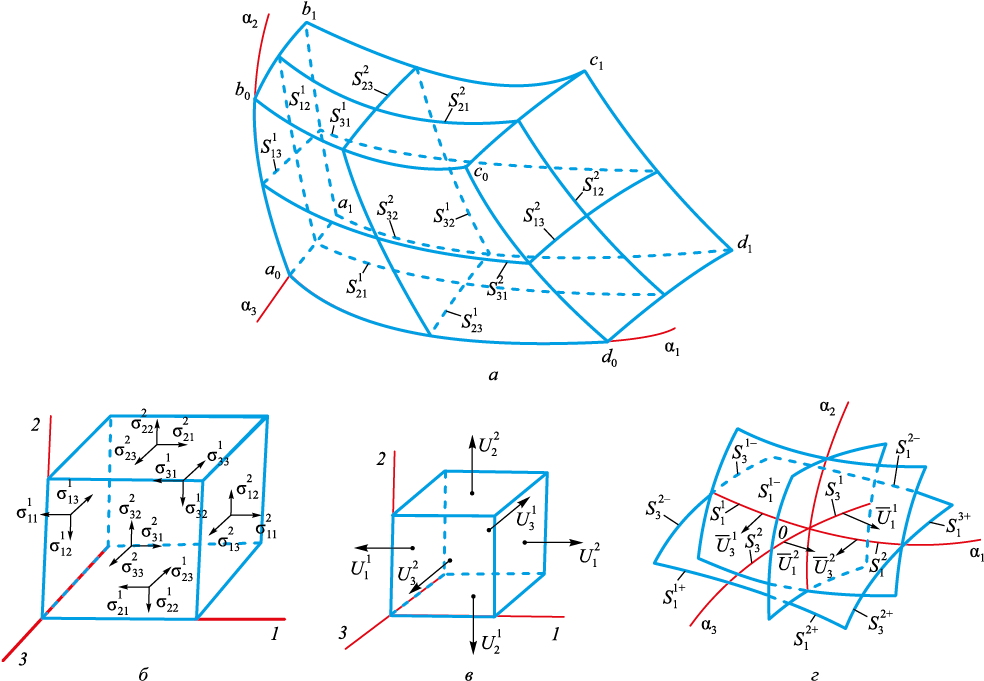
Для решения системы (2) использовался численный метод [32]. Согласно этому методу область деформирования разбивается на конечное число ортогональных криволинейных элементов (рис. 2, а).
Рис. 2. Область деформирования: |
При осевой симметрии имеем σ31 = σ32 = 0; σ13 = σ23 = 0; U3 = 0.
В соответствии с работой [32], уравнения (2) и значения εii с учетом осевой симметрии запишутся:
| \[\begin{array}{c}{S_{13}}\Delta {S_{12}}({\sigma _{11}} - {\sigma _{22}}) + {S_{12}}{S_{13}}({\sigma _{11}} - {\sigma _{33}}) + \\ + 0,5\Delta {\sigma _{11}}{S_{12}}{S_{13}} + 0,5\Delta {\sigma _{12}}{S_{21}}{S_{23}} + \\ + ({S_{21}}\Delta {S_{23}} + 2{S_{23}}\Delta {S_{21}}){\sigma _{21}} = 0;\\{S_{21}}\Delta {S_{23}}({\sigma _{22}} - {\sigma _{33}}) + {S_{23}}{S_{21}}({\sigma _{22}} - {\sigma _{11}}) + \\ + 0,5\Delta {\sigma _{22}}{S_{23}}{S_{21}} + 0,5\Delta {\sigma _{21}}{S_{12}}{S_{13}} + \\ + ({S_{12}}\Delta {S_{13}} + 2{S_{13}}\Delta {S_{12}}){\sigma _{21}} = 0;\end{array}\] | (4) |
| \[\begin{array}{c}{\sigma _{11}} - {\sigma _{22}} = 2{G_p}({\varepsilon _{11}} - {\varepsilon _{22}});\\{\sigma _{22}} - {\sigma _{33}} = 2{G_p}({\varepsilon _{22}} - {\varepsilon _{33}});\end{array}\] | (5) |
| \[{\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _{33}} = 3{k_p}\sigma + 3{\alpha _p}(\theta - \theta _p^*);\] | (6) |
| \[\begin{array}{c}{\varepsilon _{11}} = \frac{{2\Delta {U_1}}}{{{S_{21}}}} + \frac{{2{U_2}}}{{{S_{21}}}}\frac{{\Delta {S_{21}}}}{{{S_{12}}}};\\{\varepsilon _{22}} = \frac{{2\Delta {U_2}}}{{{S_{32}}}} + \frac{{2{U_1}}}{{{S_{12}}}}\frac{{\Delta {S_{12}}}}{{{S_{21}}}};\\{\varepsilon _{33}} = \frac{{2{U_1}}}{{{S_{13}}}}\frac{{\Delta {S_{13}}}}{{{S_{31}}}} + \frac{{2{U_2}}}{{{S_{23}}}}\frac{{\Delta {S_{23}}}}{{{S_{32}}}};\end{array}\] | (7) |
здесь \({U_i} = U_i^1 + U_i^2,{\rm{ }}\Delta {U_i} = U_i^2 - U_i^1,\) (i = 1, 2); \({S_{ij}} = S_{ij}^1 + S_{ij}^2;{\rm{ }}\Delta {S_{ij}} = S_{ij}^2 - S_{ij}^1.\)
Принятая символика описана в работах [1; 7].
Уравнения (4) – (7) записаны с учетом того, что \(\frac{{\partial {U_1}}}{{\partial {x_3}}} = 0,{\rm{ }}\frac{{\partial {\sigma _{3i}}}}{{\partial {x_3}}} = 0;\) i = 1, 2, 3; для тел вращения имеет место ΔS31 = 0; ΔS32 = 0; \(\frac{{\Delta {U_1}}}{{{S_3}}} = 0;{\rm{ }}\frac{{\Delta {U_2}}}{{{S_3}}} = 0;\) U3 = 0; на поверхности x1x3 : \(S_2^ + - S_2^ - = 0;\) на поверхности x2x3 : \(S_2^ + - S_2^ - = 0;\) сдвиговые значения εij (i ≠ j) запишутся для узла (0) (рис. 2, г) в виде
| \[\begin{array}{c}\varepsilon _{12}^0 = \frac{{2\Delta {{\bar U}_2}}}{{{S_1}}} - 0,5{{\bar U}_2}\frac{{S_2^ + - S_2^ - }}{{{S_1}{S_2}}} + \\ + \frac{{2\Delta {{\bar U}_1}}}{{{S_2}}} - 0,5{{\bar U}_1}\frac{{S_1^ + - S_1^ - }}{{{S_1}{S_2}}},\end{array}\] | (8) |
где \({S_i} = S_i^1 + S_i^2;{\rm{ }}\Delta {\bar U_l} = {\bar U_{{l_2}}} - {\bar U_{{l_1}}};{\rm{ }}S_i^ + = S_i^{1 + } + S_i^{2 + };\) \(S_i^ - = S_i^{1 - } + S_i^{2 - };\) \({\bar U_l}\) ‒ среднее от значения Ui по граням элемента.
В работе [32] доказано, что разностный аналог системы (4) – (6) с учетом уравнения (7) при наличии начальных и граничных условий является определимым. Размерность системы (4) – (6) значительно сокращается при осуществлении следующих операций.
1. Разности (σij – σjj) в уравнениях (4) выражаются через формулу (5).
2. Уравнение сохранения массы переписывается в рекуррентной форме с учетом выражений (7) в виде \(U_1^2\) = \(U_1^1\) + [A]; здесь [A] – оператор, не содержащий \(U_1^2\); направление обхода области по x1 (→), по x2 (↑).
3. Определяются сдвиговые выражения εij (i ≠ j) по внутренним узлам сетки в соответствии с формулами (8); i = 1, j = 2.
4. Определяются значения σij (i ≠ j) по внутренним узлам сетки из уравнений состояния \(\sigma _{12}^0 = G_p^0\varepsilon _{12}^0.\)
5. Определяются величины σij по внешним узлам сетки из граничных условий, а на контактных поверхностях – из закона трения.
6. Определяются σij по граням элементов как средние от значений σij в узлах граней.
7. Первое уравнение (4) переписывается в рекуррентном виде \(\sigma _{11}^1\) = \(\sigma _{11}^2\) + [Б]; здесь [Б] – оператор, не содержащий \(\sigma _{11}^1\); направление обхода области по x1 (←), по x2 (↓).
8. Из системы уравнений (второе уравнение в системе (4) и уравнение σ22 – σ11 = 2λ(ε11 – ε22)) определяются значения \(\sigma _{22}^1\) и \(\sigma _{22}^2\) для элемента, составляются уравнения вида \({F_3} = {(\sigma _{22}^2)_{IJ}} - {(\sigma _{22}^1)_{IJ + 1}} = 0\) для внутренних граней (где J – индекс элемента по координате x2 ).
Таким образом, если считать независимыми переменными \(X = \left\{ {{U_2},} \right.{\left. {{\rm{ }}{U_1}} \right|_{{x_1} = 0}},{\left. {{\rm{ }}{\sigma _{11}}} \right|_{{x_1}}} = \left. {x_1^*} \right\},\) то по последовательности (1) ‒ (7) можно определить зависимые переменные через X (\(x_1^*\) ‒ конечное значение координаты x по криволинейной области).
Эквивалентная система уравнений имеет вид
| \[\begin{array}{c}{F_1} = (U_1^2 - U_1^*{\left. ) \right|_{{x_1} = x_1^*}} = 0;\\{F_2} = (\sigma _{11}^1 - \sigma _{11}^*{\left. ) \right|_{{x_1} = 0}} = 0;{\rm{ }}\\{F_3} = 0;\end{array}\] | (9) |
здесь \(U_1^*\) – известные из граничных условий перемещения U1 на границе области (x1 = \(x_1^*\)); \(\sigma _{11}^*\) – известные из граничных условий напряжения σ11 на границе области (x1 = 0).
Уравнений F1 = 0 столько, сколько неизвестных \({\left. {{\sigma _{11}}} \right|_{{x_1} = x_1^*}},\) а уравнений F2 = 0 столько, сколько неизвестных \({\left. {{U_1}} \right|_{{x_1}}}\) = 0.
Коэффициенты и свободные члены новой эквивалентной системы уравнений (9) можно найти с помощью следующей процедуры.
Пусть эквивалентная система уравнений имеет вид
| \[{\bar F_i} = {\alpha _{ij}}{x_j} + {b_i} = 0;{\rm{ }}i,{\rm{ }}j = 1,{\rm{ }}...,{\rm{ }}n.\] | (10) |
Если считать, что все неизвестные равны нулю (xi = 0, i = 1, ..., n), то по вышеприведенной последовательности (1) ‒ (7) и расчете \({\bar F_i}\) по формулам (9) найдем свободные члены новой системы (10):
\[{\bar F_i}^0 = {b_i};{\rm{ }}i = 1,{\rm{ }}...,{\rm{ }}n.\]
Далее находим коэффициенты aij . Для этого считаем xk = 1, xi = 0 (i ≠ k; i = 1, ..., n). По указанной выше последовательности находим значение \(\bar F_i^k\) и aik по следующей формуле:
\[{a_{ik}} = F_i^k - F_i^0,{\rm{ }}i = 1,{\rm{ }}...,{\rm{ }}n.\]
Таким образом, определяется вся матрица aik новой эквивалентной системы, которая решается по стандартной программе. Размерность эквивалентной системы сокращается примерно в 10 раз по сравнению с исходной.
Для решения уравнения теплопроводности используется численный метод [1; 32]. В соответствии с рассматриваемым методом для каждого внутреннего k-го элемента (рис. 2, а) записывается из теплового баланса система теплопроводности в разностном виде с учетом осевой симметрии и строится итерационная процедура, которая с учетом того, что тепловой поток по x3 равен нулю, представляется итерационной формулой:
| \[\begin{array}{c}{\theta _k} = \frac{{\theta _k^* + {t_{12}}\theta _1^ + + {t_{11}}\theta _1^ - + {t_{22}}\theta _2^ + + {t_{21}}\theta _2^ - }}{{1 + {t_{12}} + {t_{11}} + {t_{22}} + {t_{21}}}};\\{t_{12}} = \frac{{2({\lambda _k} + \lambda _1^ + )}}{{{S_{21}} + S_{21}^ + }}F_1^2\frac{{\Delta \tau }}{{{C_k}{\gamma _k}{V_k}}};\\{t_{11}} = \frac{{2({\lambda _k} + \lambda _1^ - )}}{{{S_{21}} + S_{21}^ + }}F_1^1\frac{{\Delta \tau }}{{{C_k}{\gamma _k}{V_k}}};\\{t_{22}} = \frac{{2({\lambda _k} + \lambda _2^ + )}}{{{S_{12}} + S_{12}^ + }}F_2^2\frac{{\Delta \tau }}{{{C_k}{\gamma _k}{V_k}}};\\{t_{21}} = \frac{{2({\lambda _k} + \lambda _2^ - )}}{{{S_{12}} + S_{12}^ - }}F_2^1\frac{{\Delta \tau }}{{{C_k}{\gamma _k}{V_k}}};\\F_i^j = S_{ik}^jS_{ip}^j;{\rm{ }}i \ne k \ne p;{\rm{ }}i,{\rm{ }}k,{\rm{ }}p = 1,2,3;{\rm{ }}j = 1,{\rm{ }}2;\\{V_k} = \frac{{{S_{13}}{S_{12}}({S_{21}} + {S_{31}})}}{{16}};\end{array}\] | (11) |
здесь \(\theta _k^*\) – средняя температура в k-ом элементе в начале временного шага Δτ; λk , θk , Ck , γk – средние теплопроводность, температура, теплоемкость и плотность в k-ом элементе в конце временного шага Δτ; \(\lambda _i^ - ,{\rm{ }}\theta _i^ - \) и \(\lambda _i^ + ,{\rm{ }}\theta _i^ + \), (i = 1, 2) – теплопроводность и температура в элементе, следующим за элементом k по координате xi в отрицательном и положительном направлениях xi ; \(S_{21}^ - = S_{21}^{1 - } + S_{21}^{2 - };\) \(S_{21}^ + = S_{21}^{1 + } + S_{22}^{2 + };\) \(S_{ij}^{1 + }\) (i ≠ j; i, j = 1, 2) и \(S_{ij}^{1 - }\) – длина дуги \(S_{ij}^1\) элемента, следующим за элементом k в положительном и отрицательном направлениях по координате xj .
В работе [32] доказывается сходимость итерационной процедуры (11).
Алгоритм решения задачи
1. Время охлаждения τ\(^*\) разбивается на конечное число шагов: \({\tau ^*} = \sum {\Delta {\tau _n}} ;\) здесь n – номер временного шага.
2. Исследуемая область разбивается на конечное число ортогональных элементов.
3. Задаются начальные и граничные условия по элементам, образующих рассматриваемую область, и константы физико-механических свойств материалов.
4. Вычисляются длины дуг элементов \(S_{ik}^j\) (i, k = 1, 2; i ≠ k; j = 1, 2).
5. Определяется поле температур на временном шаге Δτn численным решением уравнения теплопроводности с использованием итерационной формулы (11) при наличии начальных и граничных условий на рассматриваемом временном шаге.
6. Если температура в области I у поверхности S2 \({\left. \theta \right|_{{S_2}}} \le {\theta _k},\) то вычисляется толщина Δn закристаллизовавшейся корочки [5]. Если \({\left. \theta \right|_{{S_2}}} > {\theta _k},\) то выполняется следующая операция.
7. Решается система уравнений (2) с учетом разностных аналогов (4) – (7) и разработанной методики [1; 32], описанной выше. Определяются поля напряжений σij и перемещений Ui (i, j = 1, 2).
8. Проводится шаг по времени; если \(\sum {\Delta {\tau _n}} < {\tau ^*},\) то выполняется операция 4; если \(\sum {\Delta {\tau _n}} = {\tau ^*}\) – процесс вычисления закончен.
При решении температурной задачи использовали граничные условия первого рода (3). Для определения θм(τ) и θ\(^*\)(τ) воспользуемся экспериментальными данными работы [1]. Аппроксимируя эти величины, получим следующее:
\[\begin{array}{c}{\theta _{\rm{м}}} = 1550 - 1,666\tau - \frac{{\tau (60 - \tau )}}{{10 + {\tau ^2}}};\\\theta \le \tau \le 60{\rm{ c}};\\{\theta ^*} = 20 + 17,3\sqrt \tau ;\end{array}\]
здесь τ – время охлаждения, с.
Время τ не превышает 60 с, так как при τ ≥ 60 с напряжения в ОФ падают и не представляют опасности ее разрушения.
Разработана математическая модель по определению НДС и температуры в ОФ при охлаждении в ней сферической отливки, с использованием которой проведено численное решение задачи по моделированию трещиностойкости сферической ОФ.
Выводы
Предпринята первая теоретическая попытка по формулированию и решению задачи определения внешних факторов, при которых сферическая оболочковая форма не будет разрушаться от возникающих в ней температурных напряжений.
На основе основополагающих уравнений теории упругости и численных методов разработаны численная схема и алгоритм решения задачи.
Предложенная методика моделирования стойкости сферической оболочки к трещинообразованию может быть рекомендована для моделирования на других функциональных оболочках.
Список литературы
1. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И., Свиридов А.В. Математическое моделирование процессов получения отливок в керамические оболочковые формы. Москва: Инновационное машиностроение; 2020:224.
2. Евстигнеев А.И., Одиноков В.И., Дмитриев Э.А., Свиридов А.В., Иванкова Е.П. Влияние внешнего теплового воздействия на напряженное состояние оболочковых форм по выплавляемым моделям. Математическое моделирование. 2021;33(1):63–76. https://doi.org/10.20948/mm-2021-01-05
3. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И. и др. Моделирование и оптимизация выбора свойств материалов и структур оболочковых форм по выплавляемым моделям. Известия вузов. Черная металлургия. 2020;63(9): 742–754. https://doi.org/10.17073/0368-0797-2020-9-742-754
4. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И. Чернышова Д.В., Евстигнеева А.А. Влияние опорного наполнителя и структуры оболочковой формы на ее трещиностойкость. Известия вузов. Черная металлургия. 2022;65(4):285–293. https://doi.org/10.17073/0368-0797-2022-4-285-293
5. Евстигнеев А.И., Дмитриев Э.А., Чернышева Д.В., Одиноков В.И., Евстигнеева А.А., Иванкова Е.П. Моделирование внешнего силового воздействия на стойкость оболочковой формы при заливке в нее стали. Математическое моделирование. 2022;34(5):61–72. https://doi.org/10.20948/mm-2022-05-04
6. Bansode S.N., Phalle V.M., Mantha S.S. Optimization of process parameters to improve dimensional accuracy of investment casting using Taguchi approach. Advances in Mechanical Engineering. 2019;11(4):1–12. https://doi.org/10.1177/1687814019841460
7. Mittal Y.G., Kamble P., Gote G., Patil Y., Patel A. K., Bernard A., Karunakaran K.P. Mathematical modelling of pattern sublimation in rapid ice investment casting. International Journal of Metalcasting. 2022;16(2):1002–1009. http://dx.doi.org/10.1007/s40962-021-00665-w
8. Kanyo J.E., Schafföner S., Uwanyuze R.S., Leary K.S. An overview of ceramic molds for investment casting of nickel superalloys. Journal of the European Ceramic Society. 2020;40(15):4955–4973. https://doi.org/10.1016/j.jeurceramsoc.2020.07.013
9. Rafique M.M.A., Iqbal J. Modeling and simulation of heat transfer phenomena during investment casting. International Journal of Heat and Mass Transfer. 2009;52(7–8):2132–2139. http://doi.org/10.1016/j.ijheatmasstransfer.2008.11.007
10. Singh R. Mathematical modeling for surface hardness in investment casting applications. Journal of Mechanical Science and Technology. 2012;26:3625–3629. http://dx.doi.org/10.1007/s12206-012-0854-0
11. Jafari H., Idris M. H., Ourdjini A. Effect of thickness and permeability of ceramic shell mould on in situ melted AZ91D investment casting. Applied Mechanics and Materials. 2014;465–466:1087–1092. http://dx.doi.org/10.4028/www.scientific.net/AMM.465-466.1087
12. Bansode S.N., Phalle V.M., Mantha S. Taguchi approach for optimization of parameters that reduce dimensional variation in investment casting. Archives of Foundry Engineering. 2019;19(1):5–12. https://dx.doi.org/10.24425/afe.2018.125183
13. Pattnaik S., Karunakar D.B., Jha P.K. Developments in investment casting process ‒ A review. Journal of Materials Processing Technology. 2012;212(11):2332–2348. https://doi.org/10.1016/j.jmatprotec.2012.06.003
14. Zhang J., Li K.W., Ye H.W., Zhang D.Q., Wu P.W. Numerical simulation of solidification process for impeller investment casting. Applied Mechanics and Materials. 2011; 80–81:961–964. https://doi.org/10.4028/www.scientific.net/AMM.80-81.961
15. Dong Y.W., Li X.L., Zhao Q., Jun Y., Dao M. Modeling of shrinkage during investment casting of thin walled hollow turbine blades. Journal of Materials Processing Technology. 2017;244:190–203. https://doi.org/10.1016/j.jmatprotec.2017.01.005
16. Rakoczy Ł., Cygan R. Analysis of temperature distribution in shell mould during thinwall superalloy casting and its effect on the resultant microstructure. Archives of Civil and Mechanical Engineering. 2018;18(4):1441–1450. https://doi.org/10.1016/j.acme.2018.05.008
17. Yameng W., Zhigang L. The design of testing methods for strength of ceramic shell mold in investment casting. Proceedings of the Asia-Pacific Conf. on Intelligent Medical 2018 & Int. Conf. on Transportation and Traffic Engineering. 2018;336–341. https://doi.org/10.1145/3321619.3321686
18. Kolczyk J., Zych J. High temperature strength of ceramic moulds applied in the investment casting method. Archives of Foundry Engineering. 2011;11(3):121–124.
19. Anglada E., Meléndez A., Maestro L., Domínguez I. Finite element model correlation of an investment casting process. Materials Science Forum. 2014;797:105–110. http://dx.doi.org/10.4028/www.scientific.net/MSF.797.105
20. Liu C., Sun J., Lai X., He B., Li F. Influence of complex structure on the shrinkage of part in investment casting process. The International Journal of Advanced Manufacturing Technology. 2015;77:1191–1203. https://doi.org/10.1007/s00170-014-6523-y
21. Liu C., Wang F., Jin S., Li F., Lai X. Permafrost analysis methodology (PAM) for ceramic shell deformation in the firing process. International Journal of Metalcasting. 2019; 13(4):953–968. http://dx.doi.org/10.1007/s40962-019-00317-0
22. Everhart W.A., Lekakh S.N., Richards V., Chen J., Li H., Chandrashekhara K. Corner strength of investment casting shells. International Journal of Metalcasting. 2013;7:21–27. https://doi.org/10.1007/BF03355541
23. Sabau A.S. Numerical simulation of the investment casting process. Transactions of American Foundry Society. 2005;113:407–417.
24. Zheng K., Lin Y., Chen W., Liu L. Numerical simulation and optimization of casting process of copper alloy water-meter shell. Advances in Mechanical Engineering. 2020;12(5): 1–12. http://dx.doi.org/10.1177/1687814020923450
25. Manzari M.T., Gethin D.T., Lewis R.W. Optimisation of heat transfer between casting and mould. International Journal of Cast Metals Research. 2000;13(4):199–206. https://doi.org/10.1080/13640461.2000.11819402
26. Rafique M.M.A., Shah U. Modeling and simulation of heat transfer phenomenon related to mold heating during investment casting. Engineering. 2020;12(5):291–314. http://dx.doi.org/10.4236/eng.2020.125024
27. Dong Y., Bu K., Zhang D. Numerical simulation of displacement field of solidification process for investment casting. In: 2008 Asia Simulation Conf. – 7th Int. Conf. on System Simulation and Scientific Computing. 2008:715–720. https://doi.org/10.1109/asc-icsc.2008.4675453
28. Upadhya G.K., Das S., Chandra U., Paul A.J. Modelling the investment casting process: a novel approach for view factor calculations and defect prediction. Applied Mathematical Modelling. 1995;19(6):354–362. https://doi.org/10.1016/0307-904X(95)90001-O
29. Khan M.A.A., Sheikh A.K. Simulation tools in enhancing metal casting productivity and quality: A review. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture. 2016;230(10):1799–1817. https://doi.org/10.1177/0954405416640183
30. Banerjee S., Sutradhar G. Analysis of casting defects in investment casting by simulation. Advances in Materials, Mechanical and Industrial Engineering: Selected Contributions from the First Int. Conf. on Mechanical Engineering, Jadavpur University, Kolkata, India. Springer International Publishing. 2019:247–271. http://dx.doi.org/10.1007/978-3-319-96968-8_12
31. Евстигнеев А.И., Одиноков В.И., Дмитриев Э.А., Чернышова Д.В., Евстигнеева А.А., Иванкова Е.П. О трещиностойкости керамической оболочковой формы по выплавляемым моделям при затвердевании в ней шарообразной стальной отливки. Литейное производство. 2022;(9):17–21.
32. Одиноков В.И., Каплунов Б.Г., Песков А.В., Баков А.В. Математическое моделирование сложных технологических процессов. Москва: Наука; 2008:178.
Об авторах
В. И. ОдиноковРоссия
Валерий Иванович Одиноков, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27)
А. И. Евстигнеев
Россия
Алексей Иванович Евстигнеев, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27)
Э. А. Дмитриев
Россия
Эдуард Анатольевич Дмитриев, д.т.н., доцент, ректор
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27)
А. Н. Намоконов
Россия
Александр Николаевич Намоконов, аспирант
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27)
А. А. Евстигнеева
Россия
Анна Алексеевна Евстигнеева, студент кафедры «Прикладная математика»
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27)
Д. В. Чернышова
Россия
Дарья Витальевна Чернышова, аспирант кафедры «Авиастроение»
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27)
Рецензия
Для цитирования:
Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Намоконов А.Н., Евстигнеева А.А., Чернышова Д.В. Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 1. Известия высших учебных заведений. Черная Металлургия. 2024;67(2):211-218. https://doi.org/10.17073/0368-0797-2024-2-211-218
For citation:
Odinokov V.I., Evstigneev A.I., Dmitriev E.A., Namokonov A.N., Evstigneeva A.A., Chernyshova D.V. Stress-strain state of ceramic shell mold during formation of spherical steel casting in it. Part 1. Izvestiya. Ferrous Metallurgy. 2024;67(2):211-218. https://doi.org/10.17073/0368-0797-2024-2-211-218