Перейти к:
Внутренние напряжения и их источники в сталях с ОЦК-кристаллической решеткой
https://doi.org/10.17073/0368-0797-2024-2-167-175
Аннотация
Методом просвечивающей дифракционной электронной микроскопии выполнены исследования тонкой структуры сталей промышленного назначения, которые обладают ОЦК-кристаллической решеткой (перлитные, феррито-перлитные и мартенситные). Проанализирована внутренняя структура зерен, определены скалярная плотность дислокаций в различных участках материала, источники внутренних напряжений и их амплитуда. Использование метода, основанного на анализе изгибных экстинкционных контуров, позволяет изучать внутренние напряжения. Изучение внутренних напряжений и их источников проведено на примере рельсовой стали Э76ХФ со структурой пластинчатого перлита после сверхдлительной эксплуатации (пропущенный тоннаж – 1770 млн т брутто). Места проведения исследования металла рельсов: вдоль центральной оси симметрии (поверхность катания) и вдоль радиуса скругления (рабочая выкружка) головки рельса на расстояниях 0, 2 и 10 мм от поверхности. По мере приближения к поверхности головки, независимо от направления исследований (вдоль радиуса скругления выкружки или вдоль оси симметрии) пластинчатый перлит постепенно заменяется на разрушенный с образованием феррито-карбидной смеси и формированием фрагментированной структуры, причем эти процессы более интенсивно протекают в рабочей выкружке. Вдоль всей центральной оси симметрии головки рельса (поверхность катания) имеет место пластический изгиб-кручение кристаллической решетки, вдоль радиуса скругления головки рельса (рабочая выкружка) на расстоянии 10 мм от поверхности – также пластический, а на расстоянии от 0 до 2 мм – упругопластический. Основным источником внутренних моментных (дальнодействующих) напряжений в рельсовой стали является избыточная плотность дислокаций. На примере стали мартенситного класса 34ХН3МФА с использованием матричных уравнений определен тип изгибного экстинкционного контура. При малых степенях пластической деформации экстинкционные контуры являются контурами изгиба или кручения, при больших степенях – контурами смешанного типа.
Ключевые слова
Для цитирования:
Попова Н.А., Никоненко Е.Л., Порфирьев М.А., Крюков Р.Е. Внутренние напряжения и их источники в сталях с ОЦК-кристаллической решеткой. Известия высших учебных заведений. Черная Металлургия. 2024;67(2):161-175. https://doi.org/10.17073/0368-0797-2024-2-167-175
For citation:
Popova N.A., Nikonenko E.L., Porfir’ev M.A., Kryukov R.E. Internal stresses and their sources in steels with BCC lattice. Izvestiya. Ferrous Metallurgy. 2024;67(2):161-175. https://doi.org/10.17073/0368-0797-2024-2-167-175
Введение
Проблема внутренних напряжений в металлах и сплавах находится в центре внимания исследователей уже много лет [1 – 3]. Это объясняется тем, что внутренние напряжения играют важную роль в формировании предела текучести [4 – 6], деформационном упрочнении [7 – 9] и особенно в разрушении кристаллических материалов [10 – 12], а именно, в зарождении [13 – 15] и раскрытии микротрещин [16 – 18]. Велика роль внутренних напряжений в эволюции дефектной структуры при различных видах термической обработки металлов, сплавов и сталей [15; 19; 20]. Кроме того, внутренние напряжения играют значимую роль при фазовых и структурных превращениях [5; 6; 15; 20 – 22]. И, наконец, нельзя не учитывать действие внутренних напряжений при получении объемных наноструктурных материалов [23] методом интенсивной пластической деформации [4; 24 – 26].
Внутренние напряжения классифицируются, прежде всего, по области их локализации. Выделяют макро-, мезо- и микронапряжения. Макронапряжения локализованы во всем образце или в значительной части его объема. Мезоскопические внутренние напряжения локализованы в объемах протяженностью от десятков до сотен микрометров. В поликристаллах мезонапряжения локализованы в объемах одного или нескольких зерен или в части объема зерна. Микроскопические поля напряжений локализованы в участках в несколько микрометров и меньше.
Существующие методы оценки внутренних напряжений можно разделить на две группы: разрушающие и неразрушающие. Разрушающие методы условно могут быть разделены на химические, термические, металлохимические и механические [27]. Применение разрушающих методов для оценки внутренних напряжений приводит к частичному или полному разрушению изделия. Все разрушающие методы обнаружения и измерения внутренних напряжений в изделиях касаются напряжений I рода, которые, в основном, определяют эксплуатационные свойства продукции.
К неразрушающим методам относятся магнитные, оптические и поляризационно-оптические [28]. Эти методы дают возможность измерять упругие деформации внутри детали без изменения ее геометрии.
И неразрушающие, и разрушающие методы являются интегральными. Область усреднения напряжений (I рода) с использованием этих методов составляет сантиметры.
Внутренние напряжения можно определять с помощью рентгеноструктурного анализа (измерение напряжений I и II рода) [29 – 31], который также относится к неразрушающим методам [32 – 34]. Область усреднения напряжений в этом случае значительно уменьшается и составляет миллиметры, но остается по-прежнему большой. Использование рентгеноструктурного анализа позволяет проводить оценку амплитуды мезоскопических внутренних напряжений [35 – 38].
Наиболее информативным методом изучения мезо- и микроскопических полей внутренних напряжений к настоящему моменту является дифракционная электронная микроскопия, которая позволяет регулировать локальность измерения внутренних напряжений в широких пределах (от сотен нанометров до сотен микрометров) [39]. В настоящей работе использован именно метод просвечивающей дифракционной электронной микроскопии.
Величины мезо- и микроскопических внутренних напряжений определяются по картине структуры материала несколькими способами: по радиусу изгиба дислокаций в плоскости скольжения [23]; по расстоянию между дислокациями и параметрами дислокационных скоплений [40]; по расстоянию между активными плоскостями скольжения [40]; по параметрам изгибных экстинкционных контуров [19; 39].
Целью настоящей работы является изучение внутренних напряжений и их источников в ОЦК-сталях методом, основанном на анализе изгибных экстинкционных контуров.
Методика исследования
Проведено изучение образцов сталей промышленного назначения с ОЦК-кристаллической решеткой (перлитные, феррито-перлитные и мартенситные), прошедших термическую обработку и подвергнутых различной пластической деформации (растяжением, сжатием, прокаткой). Исследования выполнены методом просвечивающей дифракционной электронной микроскопии (ПЭМ) на тонких фольгах на электронных микроскопах ЭМ-125К с использованием гониометрической приставки и ЭМ-I25, обладающем более высокой разрешающей способностью. Фольги готовили методом электрополировки с использованием специальных режимов, позволяющих получить большие площади при просмотре в электронном микроскопе. Рабочее увеличение в колонне микроскопа составляло 25 000 крат. В результате проведенных исследований проанализирована внутренняя структура зерен и определена скалярная плотность дислокаций в различных участках материала, выявлены источники внутренних напряжений и определена их амплитуда. Величину скалярной плотности дислокаций определяли методом секущих [39].
Определение внутренних напряжений методом ПЭМ
Незаряженный дислокационный ансамбль (то есть ансамбль без избыточных дислокаций) дает внутреннее напряжение сдвига (полей напряжений, создаваемых дислокационной структурой), определяемое по формуле [2; 6; 13 – 15; 20]
| \[\sigma = m\alpha Gb\sqrt \rho ,\] | (1) |
где m – ориентационный множитель или фактор Шмида [20]; α – параметр, зависящий от типа дислокационного ансамбля (для незаряженного дислокационного ансамбля α = 0,05 ÷ 1,00 [2; 6; 19]); G – модуль сдвига; b – вектор Бюргерса; ρ – скалярная плотность дислокаций.
В случае заряженного дислокационного ансамбля, когда присутствует избыточная плотность дислокаций ρ± = ρ+ – ρ– ≠ 0, создаются внутренние моментные (или дальнодействующие) напряжения. Наличие избыточной плотности дислокаций и, соответственно, внутренние моментные напряжения идентифицируются по наличию в материале изгибных экстинкционных контуров. Эти контуры являются результатом дифракционного контраста, наблюдаемого на электронно-микроскопическом изображении структуры сильно деформированного кристалла.
Изгиб кристаллической решетки может быть [6; 12 – 15; 20; 23]: чисто упругим, создаваемым полями напряжений, накопленными из-за несовместности деформации (например, зерен поликристалла, матрицы материала и недеформируемыми частицами); пластическим, если изгиб создается дислокационными зарядами (то есть избыточной плотностью дислокаций, локализованной в некотором объеме материала); упругопластическим, когда в материале присутствуют оба источника полей.
По наличию в материале изгибных экстинкционных контуров методом ПЭМ можно измерить внутренние (моментные или дальнодействующие) напряжения. Именно их присутствие приводит к изгибу фольги (что соответствует кривизне-кручению кристаллической решетки), если фольга сохраняет форму пластины [39]. Процедура измерения величины внутренних моментных (дальнодействующих) напряжений сводится к определению градиента кривизны фольги (кристаллической решетки):
| \[\chi = \frac{{\partial \varphi }}{{\partial l}},\] | (2) |
где ∂φ = Δφ – изменение ориентировки отражающей плоскости фольги; ∂l = Δl – перемещения изгибного экстинкционного контура.
Величина χ определяется путем смещения экстинкционного контура на Δl при контролируемом угле наклона фольги Δφ в колонне микроскопа с помощью гониометра. Специальными опытами установлено, что ширина контура в величинах разориентировок для ОЦК-сталей составляет ~1° [6; 20]. Это означает, что при повороте гониометра на величину Δφ ≈ 1° изгибный экстинкционный контур смещается на расстояние, равное своей ширине, то есть Δl ≈ l.
Для разделения случаев пластического, упругого и упругопластического изгибов необходимо сравнить скалярную плотность дислокаций (ρ), измеренную в локальном участке вблизи изгибного экстинкционного контура, с избыточной плотностью дислокаций (ρ±), измеренную локально по градиенту разориентировки [20; 23]:
| \[{\rho _ \pm } = \frac{1}{b}\frac{{\partial \varphi }}{{\partial l}} = \frac{\chi }{b}.\] | (3) |
В случае, если в исследуемом участке фольги оказывается ρ ≥ ρ± , то изгиб кристаллической решетки можно считать пластическим. Определенная по формуле (2) амплитуда кривизны-кручения кристаллической решетки χ = χпл , а амплитуда внутренних моментных напряжений, созданных пластическим изгибом,
| \[\sigma _{\rm{д}}^{{\rm{пл}}} = m\alpha Gb\sqrt {{\rho _ \pm }} = m\alpha G\sqrt {b{\chi _{{\rm{пл}}}}} ,\] | (4) |
где α = 0,05 ÷ 0,60 – параметр, зависящий от типа дислокационного ансамбля [23].
Необходимо отметить, что величина α в формуле (4) практически не зависит от исследуемого материала (металл, сплав или сталь) и определяется лишь типом сформировавшейся субструктуры [23].
В случае, если в исследуемом участке фольги вблизи изгибного экстинкционного контура оказывается ρ = 0, то изгиб кристаллической решки чисто упругий. Амплитуда кривизны-кручения кристаллической решетки, определенная по формуле (2), χ = χупр , а амплитуда внутренних моментных напряжений, созданных упругим изгибом, должна быть определена по формуле [20; 23]
| \({\rm{\sigma }}_{\rm{д}}^{\rm{у}} = \;m{{\rm{\alpha }}_{\rm{c}}}Gt\frac{{\partial \phi }}{{\partial \ell }}\; = \;m{{\rm{\alpha }}_{\rm{c}}}Gt{{\rm{\chi }}_{{\rm{упр}}}},\) | (5) |
где αс = 1,0 ÷ 1,5 – коэффициент Струнина [20], рассчитанный для дислокационного ансамбля, составленного из дислокаций одного знака; t – толщина фольги.
Если вблизи изгибного экстинкционного контура оказывается ρ < ρ± , то изгиб кристаллической решетки упругопластический и тогда величина ρ± является условной. В этом случае проводится разделение изгиба кристаллической решетки на пластическую компоненту, для которой ρ = \({\rho '_ \pm }\), и упругую компоненту, для которой \({\rho ''_ \pm }\) = ρ± – \({\rho '_ \pm }\). Амплитуда кривизны кручения кристаллической решетки
| χ = χпл + χупр , | (6) |
где χ рассчитывается по формуле (2), χпл = b\({\rho '_ \pm }\) = bρ и поэтому
| χупр = χ – χпл . | (7) |
В результате амплитуда внутренних моментных (дальнодействующих) напряжений определяется как
| \[{\sigma _{\rm{д}}} = \sigma _{\rm{д}}^{{\rm{пл}}} + \sigma _{\rm{д}}^{\rm{у}},\] | (8) |
где \(\sigma _{\rm{д}}^{{\rm{пл}}}\) определяется по формуле (4), а \(\sigma _{\rm{д}}^{\rm{упр}}\) – по формуле (5):
| \[\sigma = m\alpha G\sqrt {b{\chi _{{\rm{пл}}}}} + m{\alpha _{\rm{c}}}Gt{\chi _{{\rm{упр}}}}.\] | (9) |
Результаты и их обсуждение
Источники внутренних напряжений в ОЦК-сталях
Единичная дислокация уже является источником внутренних напряжений. Поля от отдельных дислокаций простираются на небольшие расстояния, много меньшие, чем расстояния между ближайшими дислокациями [39]. Более эффективными источниками внутренних напряжений являются группы дислокаций: они охватывают весь микроуровень и создают поля значительно большей амплитуды [40]. К таким дислокационным группам относятся, прежде всего, распределенные дислокационные заряды (избыточные дислокации одного знака) [41]. Однако большие группы дислокаций одного знака встречаются редко. Чаще в материале присутствуют неоднородно распределенные дислокации разных знаков с избыточной плотностью дислокаций. Такие образования, несмотря на внутреннее экранирование, создают поля внутренних напряжений [41].
Другой тип дислокационных образований, создающий более значительные внутренние напряжения, это различные дислокационные границы. Как правило, они содержат неравное количество дислокаций разных знаков и могут вводить разориентировку. Их основное отличие заключается в том, что дислокации в границах принадлежат разным плоскостям скольжения, в то время как в дислокационных зарядах дислокации находятся на одной или на близких плоскостях скольжения.
К другим источникам внутренних напряжений относятся границы зерен, стыки зерен, уступы на межзеренных границах [41; 42]. Причиной возникновения этих внутренних напряжений является, прежде всего, несовместность деформации соседних зерен. Такая несовместность присутствует всегда, несмотря на действие аккомодационных систем скольжения. Вторая причина – наличие решеточных дислокаций, вошедших в границы зерен, и зернограничных источников дислокаций. Мощным источником внутренних напряжений являются частичные дисклинации в стыках зерен и в уступах на межфазных границах, то есть стыковые дисклинации [43].
Все перечисленные источники – это источники внутренних напряжений пластического происхождения.
Источниками внутренних напряжений упругого происхождения, которые возникают, в основном, при неоднородной деформации материала, являются, прежде всего, микротрещины [6; 12 – 15; 41]. Еще одним источником внутренних напряжений является бейновская деформация [20], которая возникает в результате искривления кристаллической решетки при фазовом γ → α-превращении в сталях. Такие напряжения возникают и в материалах, упрочненных дисперсными недеформируемыми частицами [23]. В случае частичной релаксации этих полей путем размножения и скольжения дислокаций они приобретают упругопластический характер [12 – 15; 41]. В зависимости от степени их взаимодействия с окружающими дислокационными структурами формирующиеся внутренние напряжения могут быть всех трех типов. В реальных материалах, особенно после значительных деформаций, поля от различных источников суммируются. В результате образуется сложное трехмерное поле внутренних напряжений.
Внутренние напряжения и их источники в рельсовой стали
Изучение внутренних напряжений и их источников после сверхдлительной эксплуатации (пропущенный тоннаж – 1770 млн т брутто) проведено на рельсах из стали Э76ХФ со структурой пластинчатого перлита. Были выполнены исследования металла рельсов вдоль центральной оси симметрии (поверхность катания) и вдоль радиуса скругления (рабочая выкружка) головки рельса на расстояниях 0, 2 и 10 мм от поверхности.
Проведенные исследования показали, что эксплуатация рельсов привела к существенному преобразованию и усложнению структуры, причем более интенсивно вдоль радиуса скругления выкружки. Так, если на расстоянии 10 мм от поверхности катания вдоль оси симметрии объемная доля пластинчатого перлита составляет 95 % и феррито-карбидной смеси (разрушенного перлита) – 5 %, то в поверхностном слое доля пластинчатого перлита – только 45 %, доля феррито-карбидной смеси – 50 %, а также присутствует фрагментированная структура (5 %). Что касается рабочей выкружки, то на расстоянии 10 мм от поверхности вдоль радиуса скругления объемная доля пластинчатого перлита составляет также 95 %, однако в поверхностном слое она уменьшается до 25 %, а доля фрагментированной структуры увеличивается до 25 %. Таким образом, по мере приближения к поверхности головки, независимо от направления исследований (вдоль радиуса скругления выкружки или вдоль оси симметрии), пластинчатый перлит постепенно заменяется на разрушенный с образованием феррито-карбидной смеси и формированием фрагментированной структуры, причем эти процессы более интенсивно протекают в рабочей выкружке.
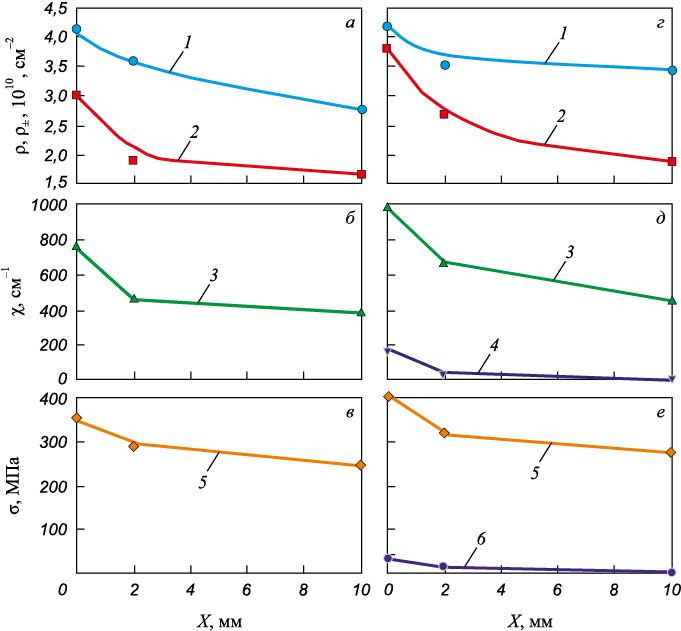
На рис. 1 показаны изменения средних по материалу количественных параметров тонкой структуры по мере приближения к поверхности головки.
Рис. 1. Изменение средних количественных параметров тонкой структуры |
Все характеристики увеличиваются при приближении к поверхности головки рельса. Несколько более интенсивно происходит увеличение скалярной (ρ) и особенно избыточной (ρ±) плотности дислокаций. Однако их поведение внутри различных структурных составляющих различно. Скалярная плотность дислокаций во всем материале независимо от направления исследований (вдоль радиуса скругления выкружки или вдоль оси симметрии) по мере приближения к поверхности увеличивается практически с одинаковой скоростью. Избыточная плотность дислокаций, определяемая из ширины изгибных экстинкционных контуров, вдоль центральной оси симметрии (поверхность катания) во всем материале остается меньше скалярной (ρ > ρ±), то есть имеет место пластический изгиб-кручение кристаллической решетки: χ = χпл и σд = \(\sigma _{\rm{д}}^{{\rm{пл}}}\) (рис. 1, а – в). Вдоль радиуса скругления выкружки в пластинчатом перлите также сохраняется выполнение условия ρ > ρ± , однако в феррито-карбидной смеси и фрагментированной структуре оказывается ρ = ρ± . Это означает, что здесь дислокационная структура полностью поляризована и в этих местах материала имеет место упругопластический изгиб кристаллической решетки: χ = χпл + χупр и \({\sigma _{\rm{д}}} = \sigma _{\rm{д}}^{{\rm{пл}}} + \sigma _{\rm{д}}^{\rm{у}}\). Несмотря на то, что величина упругой составляющей небольшая (рис. 1, д, е), не считаться с такими участками в структуре материала нельзя, так как именно в таких местах наиболее вероятно зарождение разрушения. Таким образом, основным источником внутренних моментных (дальнодействующих) напряжений в рельсовой стали является избыточная плотность дислокаций. Однако присутствуют и другие источники внутренних напряжений, а именно: границы раздела феррита и цементита; границы фрагментов и частицы цементита, расположенные на границах и внутри фрагментов (рис. 2).
Рис. 2. ПЭМ-изображения изгибных экстинкционных контуров (указаны стрелками) |
Влияние пластической деформации на кривизну-кручение кристаллической решетки в ОЦК-стали
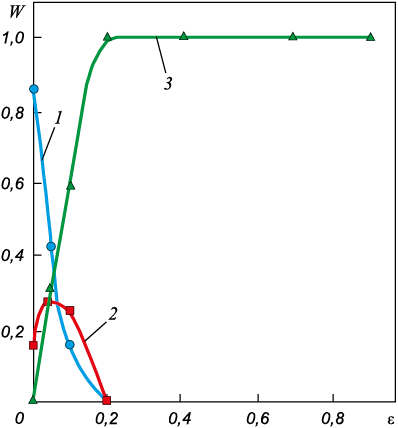
Известно [6; 23], что с развитием деформации нарастает градиент кривизны-кручения по материалу. Это проявляется как в изменении ширины экстинкционных контуров вдоль их длины, так и в их искривлении. Изменяется и тип контуров. В общем случае величина кривизны-кручения кристаллической решетки χ является тензором 2-го ранга [6; 44; 45]. Тензор содержит компоненты кривизны и кручения кристаллической решетки χ. Поэтому, используя матричные уравнения [6], можно определить тип контура. Это было сделано в стали мартенситного класса 34ХНЗМФА. Перед деформацией экстинкционные контуры были либо контурами кривизны (изгиба/наклона) (рис. 3, кривая 1), либо кручения (рис. 3, кривая 2). Причем доля контуров кривизны была преобладающей (до 0,85). Увеличение степени пластической деформации привело к усложнению картины контуров: появляются контуры смешанного типа, доля которых нарастает; при ε ≥ 0,2 все изгибные контуры являются контурами смешанного типа (рис. 3, кривая 3).
Рис. 3. Изменение объемной доли изгибных экстинкционных контуров кривизны (1), |
Выводы
Проведен анализ источников внутренних напряжений, имеющих место в ОЦК-сталях. Показано, что вся совокупность источников может быть условно разделена на источники внутренних напряжений пластического, упругого и упругопластического происхождения.
Проведенный ПЭМ-анализ в рельсах из стали Э76ХФ после пропущенного тоннажа 1770 млн т брутто показал: по мере приближения к поверхности головки рельса пластинчатый перлит постепенно заменяется на разрушенный с образованием феррито-карбидной смеси и фрагментированной структуры, причем этот процесс более интенсивно протекает в рабочей выкружке; вдоль всей центральной оси симметрии головки рельса имеет место пластический изгиб-кручение кристаллической решетки, вдоль радиуса скругления головки рельса на расстоянии до 2 мм – упругопластический; основным источником внутренних моментных напряжений является избыточная плотность дислокаций.
В стали мартенситного класса 34ХН3МФА показано, что при малых степенях деформации экстинкционные контуры являются контурами изгиба или кручения, при больших – все контуры смешанного типа.
Список литературы
1. Koneva N.A., Kozlov E.V., Trishkina L.I. Internal field sources, their screening and the flow stress. Materials Science and Engineering: A. 2001;319-321:156–159. https://doi.org/10.1016/S0921-5093(01)00945-5
2. Конева Н.А., Козлов Э.В. Дислокационная структура и физические механизмы упрочнения металлических материалов. В кн.: Перспективные материалы. Структура и методы исследования (учебное пособие) / Под ред. Д.Л. Мерсона. Тула: ТГУ; Москва: МИСиС; 2006:267–320.
3. Ovid’ko I.A., Valiev R.Z., Zhu Y.T. Review on superior strength and enhanced ductility of metallic nanomaterials. Progress in Materials Science. 2018:94:462–540. https://doi.org/10.1016/j.pmatsci.2018.02.002
4. Закономерности пластической деформации в высокопрочных и нанокристаллических металлических материалах / А.Н. Тюменцев, А.Д. Коротаев, И.А. Дитенберг, Ю.П. Пинжин, В.М. Чернов. Новосибирск: СО РАН Наука; 2018:256.
5. Yang M., Pan Yu., Yuan F., Zhu Yu., Wu X. Back stress strengthening and strain hardening in gradient structure. Materials Research Letters. 2016;4(3):145–151. https://doi.org/10.1080/21663831.2016.1153004
6. Конева Н., Киселева С., Попова Н. Эволюция структуры и внутренние поля напряжений. Аустенитная сталь. Германия: LAP LAMBER Academic Publishing; 2017:156.
7. Kundu A., Field D.P. Geometrically necessary dislocation density evolution in interstitial free steel at small plastic strains. Metallurgical and Materials Transactions A. 2018;49:3274–3282. https://doi.org/10.1007/s11661-018-4693-1
8. Kundu A., Field D.P., Chakraborti P.C. Effect of strain and strain rate on the development of deformation heterogeneity during tensile deformation of a solution annealed 304 LN austenitic stainless steel: An EBSD study. Materials Science and Engineering: A. 2019;773:138854. https://doi.org/10.1016/j.msea.2019.138854
9. Muñoz J.A., Komissarov A. Back stress and strength contributions evolution of a heterogeneous austenitic stainless steel obtained after one pass by equal channel angular sheet extrusion (ECASE). The International Journal of Advanced Manufacturing Technology. 2020;109:607–617. https://doi.org/10.1007/s00170-020-05630-1
10. Ivanov Yu.F., Gromov V.E., Yuriev A.A., Kormyshev V.E., Rubannikova Yu.A., Semin A.P. Deformation strengthening mechanisms of rails in extremely long-term operation. Journal of Materials Research and Technology. 2021;11: 710–718. https://doi.org/10.1016/J.JMRT.2020.12.107
11. Yuriev A.A., Ivanov Yu.F., Gromov V.E., Rubannikova Yu.A., Starostenkov M.D., Tabakov P.Y. Structure and properties of lengthy rails after extreme long-term operation. MRF; 2021;106:193. https://doi.org/10.21741/9781644901472
12. Ivanov Yu.F., Gleser A.M., Kuznetsov R.V., Gromov V.E., Shliarova Yu.A., Semin A.P., Sundeev R.V. Fine structure formation in rails under ultra long-term operation. Materials Letters. 2022;309(4):131378. https://doi.org/10.1016/j.matlet.2021.131378
13. Смирнов А.Н., Козлов Э.В. Субструктура, внутренние поля напряжений и проблема разрушения паропроводов из стали 12Х1МФ. Кемерово: Кузбассвузиздат; 2004:163.
14. Сварка модулированным током. Структурно-фазовое состояние и поля внутренних напряжений в сварных соединениях конструкционных сталей / А.Н. Смирнов, А.Ф. Князьков, В.Л. Князьков и др. Москва: Инновационное машиностроение; Кемерово: Сибирская издательская группа; 2017:328.
15. Смирнов А.Н., Князьков А.Ф., Князьков В.Л. и др. Структурно-фазовое состояние, контроль и испытания сварных соединений аустенитных нержавеющих сталей. Кемерово: Сибирская издательская группа; 2021:248.
16. Panin V.E., Egorushkin V.E. Fundamental role of local curvature of crystal structure in plastic deformation and fracture of solids. Physical Mesomechanics of Multilevel Systems 2014: AIP Conference Proceedings. 2014;1623(1):475–478. https://doi.org/10.1063/1.4898985
17. Панин В.Е., Панин А.В., Елсукова Т.Ф., Попкова Ю.Ф. Фундаментальная роль кривизны кристаллической структуры в пластичности и прочности твердых тел. Физическая мезомеханика. 2014;17(6):7–18.
18. Cattivelli A., Roy M.J., Burke M.G, Dhers J., Lee T.L., Francis J.A. Internal stresses in a clad pressure vessel steel during post weld heat treatment and their relevance to underclad cracking. International Journal of Pressure Vessels and Piping. 2021;193:104448. https://doi.org/10.1016/j.ijpvp.2021.104448
19. Fang X.-Y., Zhang H.-N., Ma D.-W., Wu Z.-J., Huang W. Influence of welding residual stress on subsurface fatigue crack propagation of rail. Engineering Fracture Mechanics. 2022;271:108642. https://doi.org/10.1016/j.engfracmech.2022.108642
20. Эволюция фазового состава, дефектной структуры, внутренних напряжений и перераспределение углерода при отпуске литой конструкционной стали / Э.В. Козлов, Н.А. Попова, О.В. Кабанина, С.И. Климашин, В.Е. Громов. Новокузнецк: изд. СибГИУ; 2007:177.
21. Kassner M.E., Geantil P., Levine L.E. Long range internal stresses in single-phase crystalline materials. International Journal of Plasticity. 2013;45:44–60. https://doi.org/10.1016/j.ijplas.2012.10.003
22. Zhang Y., Yu T., Xu R., Thorborg J., Liu W., Tischler J., Godfrey A., Jensen D.J. Local residual stresses and microstructure within recrystallizing grains in iron. Materials Characterization. 2022;191:112113. https://doi.org/10.1016/j.matchar.2022.112113
23. Glezer A.M., Kozlov E.V., Koneva N.A., Popova N.A., Kurzina I.A. Plastic Deformation of Nanostructured Materials. Boca Raton, London, New York: CRC Press, Taylor & Francis Group; 2017:334. http://dx.doi.org/10.1201/9781315111964
24. Valiev R.Z., Zhilyaev A.P., Langdon T.G. Bulk Nanostructured Materials: Fundamentals and Applications. Hoboken: Wiley/TMS; 2014:440. https://doi.org/10.1002/9781118742679
25. Vinogradov A., Estrin Y. Analytical and numerical approaches to modelling severe plastic deformation. Progress in Materials Science. 2018;95:172–242. https://doi.org/10.1016/j.pmatsci.2018.02.001
26. Wilde G., Divinski S. Grain boundaries and diffusion phenomena in severely deformed materials. Materials Transactions. 2019;60(7):1302–1315. https://doi.org/10.2320/matertrans.MF201934
27. Буркин С.П., Шимов Г.В., Андрюкова Е.А. Остаточные напряжения в металлопродукции. Екатеринбург: изд. Уральского университета; 2015:248.
28. Экспериментальная механика. В 2-х книгах / Пер. с англ.; под ред. А. Кобаяси. Москва: Мир; 1990.
29. Reynolds A.P., Tang W., Gnaupel-Herold T., Prask H. Structure, properties, and residual stress of 304L stainless steel friction stir welds. Scripta Materialia. 2003;48(9):1289–1294. https://doi.org/10.1016/S1359-6462(03)00024-1
30. Cihak U., Staron P., Clemens H., Homeyer J., Stockinger M., Tockner J. Characterization of residual stresses in turbine discs by neutron and high-energy X-ray diffraction and comparison to finite element modeling. Materials Science and Engineering: A. 2006;437(1):75–82. https://doi.org/10.1016/j.msea.2006.04.049
31. Withers P.J. Mapping residual and internal stress in materials by neutron diffraction. Comptes Rendus Physique. 2007; 8(7-8):806–820. https://doi.org/10.1016/j.crhy.2007.09.015
32. Withers P.J., Turski M., Edwards L., Bouchard P.J., Buttle D.J. Recent advances in residual stress measurement. International Journal of Pressure Vessels and Piping. 2008; 85(3):118–127. https://doi.org/10.1016/j.ijpvp.2007.10.007
33. Sekimoto K. Internal stress as a link between macroscale and mesoscale mechanics. In: Chemomechanical Instabilities in Responsive Materials. 2009:241–250. https://doi.org/10.1007/978-90-481-2993-5_10
34. Wong S.L., Dawson P.R. Evolution of the crystal stress distributions in face-centered polycrystals subjected to cyclic loading. Acta Materialia. 2011;59(18):6901–6916. https://doi.org/10.1016/j.actamat.2011.07.042
35. McNelis K.P., Dawson P.R., Miller M.P. A two-scale methodology for determining the residual stresses in polycrystalline solids using high energy X-ray diffraction data. Journal of the Mechanics and Physics of Solids. 2013;61(2):428–449. https://doi.org/10.1016/j.jmps.2012.09.015
36. Demir E., Park J.-S., Miller M.P., Dawson P.R. A computational framework for evaluating residual stress distributions from diffraction-based lattice strain data. Computer Methods in Applied Mechanics and Engineering. 2013;265:120–135. https://doi.org/10.1016/j.cma.2013.06.002
37. Skrotzki W. Deformation heterogeneities in equal channel angular pressing. Materials Transactions. 2019;60(7): 1331–1343. https://doi.org/10.2320/matertrans.MF201926
38. Yildirim C., Jessop C., Ahlström J., Detlefs C., Zhang Y. 3D mapping of orientation variation and local residual stress within individual grains of pearlitic steel using synchrotron dark field X-ray microscopy. Scripta Materialia. 2021;197:113783. https://doi.org/10.1016/j.scriptamat.2021.113783
39. Hirsch P.B., Howrie A., Nicholson R.B., Pashley D.W., Whelan M.J. Electron Microscopy of Thin Crystals. London: Butterworths; 1965:549.
40. Мадер С., Зеегер А., Лейтц К. Деформационное упрочнение и распределение дислокаций в ГЦК металлах. В кн.: Материалы конференции «Структура и механические свойства металлов», Теддингтон, Мидлсекс, 7 – 9 января 1963 г. Москва: Металлургия; 1967;384.
41. Конева Н.А., Тришкина Л.И., Жданов А.Н., Перевалова О.Б., Попова Н.А., Козлова Э.В. Источники полей напряжений в деформированных поликристаллах. Физическая мезомеханика. 2006;9(3):93–102.
42. Громова А.В., Юрьев А.Б., Иванов Ю.Ф., Чинокалов В.Я. Формирование дальнодействующих полей напряжений при волочении проволоки. Известия вузов. Черная металлургия. 2006;49(2):27–31.
43. Рыбин В.В. Закономерности формирования мезоструктур в ходе развития пластической деформации. Вопросы материаловедения. 2002;29(1):11–33.
44. Calcaynotto M., Ponge D., Demir E., Raabe D. Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD. Materials Science and Engineering: A. 2010;527(10-11): 2738–2746. https://doi.org/10.1016/j.msea.2010.01.004
45. Kundu A., Field D.P. Influence of plastic deformation heterogeneity on development of geometrically necessary dislocation density in dual phase steel. Materials Science and Engineering: A. 2016;667:435–443. https://doi.org/10.1016/j.msea.2016.05.022
Об авторах
Н. А. ПоповаРоссия
Наталья Анатольевна Попова, к.т.н., научный сотрудник научно-учебной лаборатории «Наноматериалы и нанотехнологии»
Россия, 634003, Томск, пл. Соляная, 2
Е. Л. Никоненко
Россия
Елена Леонидовна Никоненко, к.ф.-м.н., доцент кафедры физики, химии, теоретической механики, Томский государственный архитектурно-строительный университет; старший преподаватель, Национальный исследовательский Томский политехнический университет
Россия, 634003, Томск, пл. Соляная, 2
Россия, 634050, Томск, пр. Ленина, 30
М. А. Порфирьев
Россия
Михаил Анатольевич Порфирьев, научный сотрудник управления научных исследований
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Р. Е. Крюков
Россия
Роман Евгеньевич Крюков, д.т.н., доцент кафедры металлургии черных металлов
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Рецензия
Для цитирования:
Попова Н.А., Никоненко Е.Л., Порфирьев М.А., Крюков Р.Е. Внутренние напряжения и их источники в сталях с ОЦК-кристаллической решеткой. Известия высших учебных заведений. Черная Металлургия. 2024;67(2):161-175. https://doi.org/10.17073/0368-0797-2024-2-167-175
For citation:
Popova N.A., Nikonenko E.L., Porfir’ev M.A., Kryukov R.E. Internal stresses and their sources in steels with BCC lattice. Izvestiya. Ferrous Metallurgy. 2024;67(2):161-175. https://doi.org/10.17073/0368-0797-2024-2-167-175
JATS XML