Scroll to:
Internal stresses and their sources in steels with BCC lattice
https://doi.org/10.17073/0368-0797-2024-2-167-175
Abstract
The paper studies fine structure of industrial steels with BCC lattice (pearlite, ferrite-pearlite and martensite) using transmission diffraction electron microscopy. The internal structure of the grains was analyzed; the scalar density of dislocations in various parts of the material, the sources of internal stresses and their amplitude were determined. The use of a method based on the analysis of bending extinction contours allowed us to study internal stresses. We analyzed the internal stresses and their sources using the example of 0.76С–Cr–V–Fe rail steel with a lamellar pearlite structure after ultra long-term operation with the tonnage of 1770 million gross tons. The metal of the rails was examined along the central axis of symmetry (rolling surface) and the rounding radius (working fillet) of the railhead at distances of 0, 2 and 10 mm from the surface. As one approaches the head surface, regardless of the research direction (along the fillet rounding radius or along the axis of symmetry), the lamellar pearlite is gradually replaced by destroyed pearlite with formation of a ferrite-carbide mixture and formation of a fragmented structure. These processes occur more intensively in the working fillet. Along the entire central axis of symmetry of the rail head (rolling surface), there is a plastic bending-torsion of the crystal lattice, along the rounding radius of the rail head (working fillet) at a distance of 10 mm from the surface – also plastic, and at a distance from 0 to 2 mm – elastic-plastic. The main source of internal torque (long-acting) stresses in rail steel is the excessive density of dislocations. Using the example of 34CrNi3MoVN steel of the martensitic class, the type of bending extinction contour was determined using mathematical equations. At low degrees of plastic deformation, extinction contours are contours of bending or torsion, at high degrees they are of a mixed type.
Keywords
For citations:
Popova N.A., Nikonenko E.L., Porfir’ev M.A., Kryukov R.E. Internal stresses and their sources in steels with BCC lattice. Izvestiya. Ferrous Metallurgy. 2024;67(2):161-175. https://doi.org/10.17073/0368-0797-2024-2-167-175
Introduction
The investigation of internal stresses in metals and alloys has long captivated researchers [1 – 3] due to their critical role in several mechanical properties and behaviors. Internal stresses significantly influence yield strength [4 – 6], deformation strengthening [7 – 9], and crucially, the fracture of crystalline materials through the initiation [10 – 15] and propagation of microcracks [16 – 18]. They are also vital in the evolution of defect structures during various thermal treatments of metals, alloys, and steels [15; 19; 20], and in phase and structural transformations [5; 6; 15; 20 – 22]. Additionally, internal stresses are indispensable in the production of bulk nanostructured materials created via intensive plastic deformation [4; 24 – 26].
Internal stresses are categorized based on their localization: macro-, meso-, and microstresses. Macrostresses span the entire sample or a substantial part thereof. Mesoscopic internal stresses are localized within volumes ranging from tens to hundreds of micrometers, often confined to one or several grain volumes or part of a grain volume. Microscopic stress fields are confined to areas a few micrometers in size or smaller.
Methods for assessing internal stresses fall into two primary categories: destructive and non-destructive. Destructive methods include chemical, thermal, metallographic, and mechanical approaches [27], which may lead to the partial or complete destruction of the sample. These methods typically assess first-order stresses, which are crucial for determining the operational properties of materials.
Non-destructive techniques encompass magnetic, optical, and polarization-optical methods [28]. These allow for the measurement of elastic deformations within a component without altering its geometry.
Both non-destructive and destructive methods provide an integral assessment of stresses, with stress (first-order stress) averaging over centimeters.
Internal stresses can also be determined using X-ray structural analysis, which measures both first and second-order stresses [29 – 31] and is considered a non-destructive method [32 – 34]. This technique reduces the range of stress averaging to millimeters, although it is still relatively broad. X-ray structural analysis is particularly effective for evaluating the amplitude of mesoscopic internal stresses [35 – 38].
Presently, the most informative method for examining meso- and microscopic internal stress fields is transmission electron diffraction microscopy, which offers precise control over the locality of stress measurements, ranging from hundreds of nanometers to hundreds of micrometers [39]. In this study, internal stresses and their sources in FCC steels were investigated using transmission electron diffraction microscopy with a focus on bending extinction contours.
Measurements of meso- and microscopic internal stresses were derived from the material’s structure, including the radius of curvature of dislocations in the slip plane [23], the spacing between dislocations, the parameters of dislocation clusters [40], and the characteristics of bending extinction contours [19; 39].
The aim of this study is to investigate internal stresses and their sources in FCC steels using a method based on the analysis of bending extinction contours.
Materials and methods
A study was conducted on samples of industrial-purpose steels with a BCC crystal lattice (pearlite, ferrite-pearlite, and martensite), which underwent heat treatment and various plastic deformation processes (stretching, compression, rolling). The research was carried out using transmission diffraction electron microscopy (TEM) on thin foils with EM-125K electron microscopes equipped with a goniometric attachment and EM-I25, which offers higher resolution capabilities. Foils were prepared using the electropolishing method with special modes to obtain larger areas for viewing in the electron microscope. The working magnification in the microscope column was set at 25,000 times. As a result of the conducted research, the internal grain structure was analyzed, and the scalar density of dislocations in different areas of the material was determined. Sources of internal stresses were identified, and their amplitude was measured. The scalar density of dislocations was determined using the intercept method [39].
Assessing internal stresses with TEM
The uncharged dislocation ensemble (i.e., an ensemble without excess dislocations) produces internal shear stress (stress fields created by the dislocation structure), determined by the equation [2; 6; 13 – 15; 20]
| \[\sigma = m\alpha Gb\sqrt \rho ,\] | (1) |
where m is the orientation multiplier or Schmid factor [20]; α is the parameter dependent on the type of dislocation ensemble (for the uncharged dislocation ensemble, α = 0.05 ÷ 1.00 [2; 6; 19]); G is the shear modulus; b is the Burgers vector; ρ is the scalar dislocation density.
In the case of a charged dislocation ensemble, when there is an excess dislocation density ρ± = ρ+ – ρ– ≠ 0, internal moment (or long-range) stresses are generated. The presence of excess dislocation density and, consequently, internal moment stresses are identified by the presence of bending extinction contours in the material. These contours result from diffraction contrast observed in electron microscopic images of a highly deformed crystal.
The bending of the crystal lattice can be [6; 12 – 15; 20; 23]: purely elastic, created by stress fields accumulated due to deformation incompatibility (for example, between grains in a polycrystal, matrix material, and non-deformable particles); plastic, if the bending is created by dislocation charges (i.e. by an excess density of dislocations localized within a certain volume of the material); elastoplastic, when both sources of fields are present in the material.
By observing bending extinction contours using the TEM method, it is possible to measure internal (moment or long-range) stresses. These stresses lead to the bending of the foil, corresponding to the curvature-torsion of the crystal lattice, if the foil retains its plate shape. The procedure for measuring the value of internal moment (long-range) stresses involves determining the curvature gradient of the foil (crystal lattice):
| \[\chi = \frac{{\partial \varphi }}{{\partial l}},\] | (2) |
where ∂φ = Δφ is the change in orientation of the reflecting foil surface; ∂l = Δl is the displacement of the bending extinction contour.
The χ value is determined by shifting the extinction contour by Δl at a controlled angle of inclination of the foil Δφ in the microscope column using a goniometer. Special experiments have shown that for BCC steels, the width of the contour in terms of disorientation is approximately 1° [6; 20]. This indicates that when the goniometer is turned by Δφ ≈ 1°, the bending extinction contour shifts a distance equal to its width, that is Δl ≈ l.
To differentiate between cases of plastic, elastic, and elastoplastic bending, it is necessary to compare the scalar dislocation density (ρ) measured in a local area near the bending extinction contour with the excess dislocation density (ρ±) measured locally based on the disorientation gradient [20; 23]:
| \[{\rho _ \pm } = \frac{1}{b}\frac{{\partial \varphi }}{{\partial l}} = \frac{\chi }{b}.\] | (3) |
If in the investigated area of the foil, ρ ≥ ρ± , then the bending of the crystal lattice can be considered plastic. The amplitude of the curvature-twist of the crystal lattice determined by Eq. (2) is χ = χpl , and the amplitude of internal stresses created by plastic bending is given by
| \[\sigma _{\rm{d}}^{{\rm{pl}}} = m\alpha Gb\sqrt {{\rho _ \pm }} = m\alpha G\sqrt {b{\chi _{{\rm{pl}}}}} ,\] | (4) |
where α = 0.05 ÷ 0.60 is the parameter depending on the type of dislocation ensemble [23].
It should be noted that the value of α in Eq. (4) is practically independent of the material under study (metal, alloy, or steel) and is determined only by the type of substructure formed [23].
If in the investigated area of the foil near the bending extinction contour, ρ = 0, then the bending of the crystal lattice is purely elastic. The amplitude of the curvature-torsion of the crystal lattice, determined by Eq. (2), is χ = χel , and the amplitude of internal moment stresses created by elastic bending should be determined as follows [20; 23]
| \({\rm{\sigma }}_{\rm{d}}^{\rm{el}} = \;m{{\rm{\alpha }}_{\rm{s}}}Gt\frac{{\partial \phi }}{{\partial \ell }}\; = \;m{{\rm{\alpha }}_{\rm{s}}}Gt{{\rm{\chi }}_{{\rm{el}}}},\) | (5) |
where αs = 1.0 ÷ 1.5 is the Strunin coefficient [20], calculated for a dislocation ensemble composed of dislocations of the same sign; t is the foil thickness.
If in the vicinity of the bending extinction contour ρ < ρ± , then the bending of the crystal lattice is elasto-plastic, and in this case, the value of ρ± is conditional. In this case, the bending of the crystal lattice is divided into a plastic component, for which ρ = \({\rho '_ \pm }\), and an elastic component, for which \({\rho ''_ \pm }\) = ρ± – \({\rho '_ \pm }\). The amplitude of the curvature-torsion of the crystal lattice is
| χ = χpl + χel , | (6) |
where χ is calculated by Eq. (2), χpl = b\({\rho '_ \pm }\) = bρ and, thus
| χel = χ – χpl . | (7) |
As a result, the amplitude of internal moment (long-range) stresses is determined as
| \[{\sigma _{\rm{d}}} = \sigma _{\rm{d}}^{{\rm{pl}}} + \sigma _{\rm{d}}^{\rm{el}},\] | (8) |
where \(\sigma _{\rm{d}}^{{\rm{pl}}}\) is determined by Eq. (4), and \(\sigma _{\rm{d}}^{\rm{el}}\) by Eq. (5):
| \[\sigma = m\alpha G\sqrt {b{\chi _{{\rm{pl}}}}} + m{\alpha _{\rm{s}}}Gt{\chi _{{\rm{el}}}}.\] | (9) |
Results and discussion
Sources of internal stresses in BCC steels
A single dislocation is inherently a source of internal stresses. The fields generated by individual dislocations extend only over small distances, much smaller than the distances between the nearest dislocations [39]. However, groups of dislocations are more effective sources of internal stresses as they cover the entire microlevel and create fields of significantly greater amplitude [40]. Such groups primarily consist of distributed dislocation charges (excess dislocations of one sign) [41]. Although large groups of dislocations of one sign are rare, materials more commonly contain unevenly distributed dislocations of different signs with an excess density. Despite internal screening, these formations generate internal stress fields [41].
Another significant type of dislocation formation that induces substantial internal stresses is various dislocation boundaries. Typically, these contain an unequal number of dislocations of different signs and can introduce misorientation. A key characteristic is that the dislocations in the boundaries are from different slip planes, in contrast to dislocation charges where dislocations reside on the same or closely related slip planes.
Other sources of internal stresses include grain boundaries, grain junctions, and steps on intergranular boundaries [41; 42]. The root cause of these stresses is primarily the incompatibility of deformation between neighboring grains. This incompatibility is always present, despite the action of accommodating slip systems. Moreover, lattice dislocations that enter the grain boundaries and sources of dislocations at these boundaries contribute further to internal stresses. Junction dislocations at grain junctions and steps on interphase boundaries are also significant sources of internal stresses [43].
These mentioned sources are primarily responsible for internal stresses of plastic origin.
On the other hand, sources of elastic origin internal stresses, which mainly arise from heterogeneous deformation of the material, include microcracks [6; 12 – 15; 41] and bainitic deformation [20], which occurs due to the distortion of the crystalline lattice during the γ → α phase transformation in steels. These stresses can also arise in materials reinforced with non-deformable dispersed particles [23]. In cases where these fields partially relax through the multiplication and slip of dislocations, they acquire an elastoplastic character [12 – 15; 41]. Depending on the degree of interaction with surrounding dislocation structures, the resultant internal stresses can exhibit all three types. In real materials, especially after significant deformations, fields from different sources combine to form a complex three-dimensional field of internal stresses.
Sources and characteristics of internal stresses in rail steel
The study of internal stresses and their sources after long-term operation (with a passing tonnage of 1770 million tons gross) was conducted on rails made of 0.76С–Cr–V–Fe steel, which has a lamellar pearlite structure. The investigation focused on the rail metal along the central axis of symmetry (rolling surface) and the radius of curvature (working fillet) of the rail head at distances of 0, 2, and 10 mm from the surface.
The research revealed that rail operation led to significant structural transformations and complications, especially along the radius of the rail head. For example, at a distance of 10 mm from the rolling surface along the axis of symmetry, the volumetric fraction of lamellar pearlite was 95 %, and the ferrite-carbide mixture (degraded pearlite) was 5 %. However, in the surface layer, the fraction of lamellar pearlite dropped to 45 %, the ferrite-carbide mixture increased to 50 %, and a fragmented structure emerged (5 %). Similarly, at a distance of 10 mm from the surface along the radius of curvature, the volumetric fraction of lamellar pearlite remained at 95 %. But in the surface layer, it decreased to 25 %, with the fragmented structure also accounting for 25 %. Thus, as one approaches the head surface, regardless of the research direction (along the radius of the rail head or the axis of symmetry), lamellar pearlite gradually transforms into a degraded form, forming a ferrite-carbide mixture and fragmented structure, with these processes being more pronounced in the working fillet.
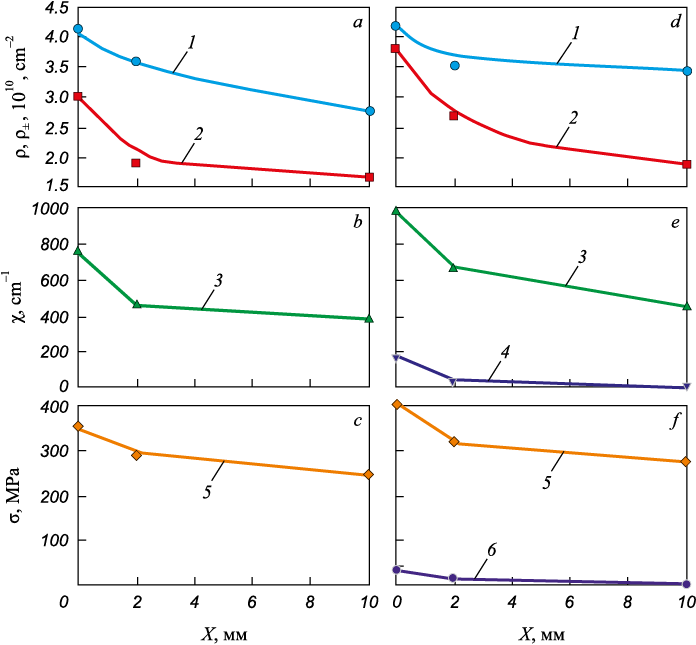
Fig. 1 illustrates the changes in the average quantitative parameters of the fine structure as we approach the head surface.
Fig. 1. Changes in the average quantitative parameters of fine structure |
All characteristics increase as we approach the surface of the rail head, with the scalar (ρ) and especially excess (ρ±) dislocation densities intensifying. However, their behavior varies within different structural components. The scalar dislocation density in the entire material, regardless of the direction of investigation (along the radius of the fillet or along the axis of symmetry), increases almost uniformly as it approaches the surface. The excess dislocation density, determined by the width of the bending extinction contours, remains smaller than the scalar density along the central axis of symmetry (rolling surface), indicating plastic bending-torsion of the crystalline lattice: χ = χpl and σl = \(\sigma _{\rm{d}}^{{\rm{pl}}}\) (Fig. 1, a – c). Along the radius of the fillet, the condition ρ > ρ± , is also met in the lamellar pearlite, but in the ferrite-carbide mixture and fragmented structure ρ = ρ± . This indicates that the dislocation structure is fully polarized in these regions of the material, and elastic-plastic bending of the crystalline lattice occurs: χ = χpl + χel and \({\sigma _{\rm{d}}} = \sigma _{\rm{d}}^{{\rm{pl}}} + \sigma _{\rm{d}}^{\rm{el}}\). Despite the minor magnitude of the elastic component (Fig. 1, e, f ), these areas are critical in the material structure as they are likely initiation points for failure. Thus, excess dislocation density is a primary source of internal momentary (long-range) stresses in rail steel. However, other sources of internal stresses include the ferrite and cementite phase boundaries, as well as boundaries of fragments and cementite particles located at the boundaries and within the fragments (Fig. 2).
Fig. 2. TEM images of bending extinction contours (indicated by arrows) |
Impact of plastic deformation on the curvature–torsion of the crystalline lattice in BCC steel
It is known [6; 23] that with the progression of deformation, the curvature-torsion gradient along the material intensifies. This phenomenon is evidenced both by the variation in the width of extinction contours along their length and by their overall bending. The type of contours also transforms. Generally, the curvature-torsion value of the crystal lattice, χ, is recognized as a second-rank tensor [6; 44; 45]. This tensor encapsulates components of both curvature and torsion of the crystal lattice. Utilizing matrix equations [6], it becomes feasible to categorize the type of contour. This method was applied to the 34C–1Cr–3Ni–1Mo–1V–Fe martensitic steel, where prior to deformation, extinction contours were identified either as curvature (bending/tilting) contours (Fig. 3, curve 1) or torsion contours (Fig. 3, curve 2). The prevalence of curvature contours was significant, accounting for up to 85 % of observations. As the degree of plastic deformation increased, the contour configuration became more complex, with mixed-type contours emerging. When the deformation reached ε ≥ 0.2, all bending contours transitioned to mixed-type contours (Fig. 3, curve 3).
Fig. 3. Change in the volume fraction of bending extinction contours of curvature (1), |
Conclusions
An analysis of the sources of internal stresses in rail steels has been conducted. It has been determined that these sources can be categorized into three types: plastic, elastic, and elastoplastic origin.
TEM analysis of 0.76С–Cr–V–Fe steel rails, which have endured a cumulative gross tonnage of 1770 million tons, revealed significant microstructural transformations as the surface of the rail head is approached. The lamellar pearlite gradually transforms into a structure featuring a ferrite-carbide mixture and fragmented structure. This process is notably more pronounced in the working fillet. Along the entire central axis of symmetry of the rail head, plastic bending-torsion of the crystal lattice is observed, while along the radius of curvature at distances up to 2 mm, the bending-torsion exhibits elastoplastic characteristics. The primary source of internal moment stresses is identified as the excess density of dislocations.
In studies of 34C–1Cr–3Ni–1Mo–1V–Fe martensitic steel, it has been observed that at low degrees of deformation, extinction contours are either bending or torsion contours. However, at higher degrees of deformation, all contours evolve into a mixed type.
References
1. Koneva N.A., Kozlov E.V., Trishkina L.I. Internal field sources, their screening and the flow stress. Materials Science and Engineering: A. 2001;319-321:156–159. https://doi.org/10.1016/S0921-5093(01)00945-5
2. Koneva N.A., Kozlov E.V. Dislocation structure and physical mechanisms of hardening of metal materials. In: Promising Materials. Structure and Methods of Research (Tutorial). Merson D.L. ed. Tula: TGU; Moscow: MISiS; 2006:267–320. (In Russ.).
3. Ovid’ko I.A., Valiev R.Z., Zhu Y.T. Review on superior strength and enhanced ductility of metallic nanomaterials. Progress in Materials Science. 2018:94:462–540. https://doi.org/10.1016/j.pmatsci.2018.02.002
4. Tyumentsev A.N., Korotaev A.D., Ditenberg I.A., Pinzhin Yu.P., Chernov V.M. Patterns of Plastic Deformation in High-Strength and Nanocrystalline Metallic Materials. Novosibirsk: SB RAS Nauka; 2018:256. (In Russ.).
5. Yang M., Pan Yu., Yuan F., Zhu Yu., Wu X. Back stress strengthening and strain hardening in gradient structure. Materials Research Letters. 2016;4(3):145–151. https://doi.org/10.1080/21663831.2016.1153004
6. Koneva N., Kiseleva S., Popova N. Evolution of the Structure and Internal Stress Fields. Austenitic Steel. Germany: LAP LAMBER Academic Publishing; 2017:156. (In Russ.).
7. Kundu A., Field D.P. Geometrically necessary dislocation density evolution in interstitial free steel at small plastic strains. Metallurgical and Materials Transactions A. 2018;49:3274–3282. https://doi.org/10.1007/s11661-018-4693-1
8. Kundu A., Field D.P., Chakraborti P.C. Effect of strain and strain rate on the development of deformation heterogeneity during tensile deformation of a solution annealed 304 LN austenitic stainless steel: An EBSD study. Materials Science and Engineering: A. 2019;773:138854. https://doi.org/10.1016/j.msea.2019.138854
9. Muñoz J.A., Komissarov A. Back stress and strength contributions evolution of a heterogeneous austenitic stainless steel obtained after one pass by equal channel angular sheet extrusion (ECASE). The International Journal of Advanced Manufacturing Technology. 2020;109:607–617. https://doi.org/10.1007/s00170-020-05630-1
10. Ivanov Yu.F., Gromov V.E., Yuriev A.A., Kormyshev V.E., Rubannikova Yu.A., Semin A.P. Deformation strengthening mechanisms of rails in extremely long-term operation. Journal of Materials Research and Technology. 2021;11: 710–718. https://doi.org/10.1016/J.JMRT.2020.12.107
11. Yuriev A.A., Ivanov Yu.F., Gromov V.E., Rubannikova Yu.A., Starostenkov M.D., Tabakov P.Y. Structure and properties of lengthy rails after extreme long-term operation. Materials Research Forum; 2021;106:193. https://doi.org/10.21741/9781644901472
12. Ivanov Yu.F., Gleser A.M., Kuznetsov R.V., Gromov V.E., Shliarova Yu.A., Semin A.P., Sundeev R.V. Fine structure formation in rails under ultra long-term operation. Materials Letters. 2022;309(4):131378. https://doi.org/10.1016/j.matlet.2021.131378
13. Smirnov A.N., Kozlov E.V. Substructure, Internal Stress Fields and the Problem of Destruction of Steam Pipelines Made of 12Kh1MF Steel. Kemerovo: Kuzbassvuzizdat; 2004:163. (In Russ.).
14. Smirnov A.N., Knyaz’kov A.F., Knyaz’kov V.L., etc. Modulated Current Welding. Structural-Phase State and Internal Stress Fields in Welded Joints of Structural Steels. Moscow: Innovatsionnoe mashinostroenie; Kemerovo: Sibirskaya izdatel’skaya gruppa; 2017:328. (In Russ.).
15. Smirnov A.N., Knyaz’kov A.F., Knyaz’kov V.L., etc. Structural-Phase State, Control and Testing of Welded Joints of Austenitic Stainless Steels. Kemerovo: Sibirskaya izdatel’skaya gruppa; 2021:248. (In Russ.).
16. Panin V.E., Egorushkin V.E. Fundamental role of local curvature of crystal structure in plastic deformation and fracture of solids. Physical Mesomechanics of Multilevel Systems 2014: AIP Conference Proceedings. 2014;1623(1):475–478. https://doi.org/10.1063/1.4898985
17. Panin V.E., Panin A.V., Elsukova T.F., Popkova Yu.F. The fundamental role of the curvature of the crystal structure in the plasticity and strength of solids. Fizicheskaya mezomekhanika. 2014;17(6):7–18. (In Russ.).
18. Cattivelli A., Roy M.J., Burke M.G, Dhers J., Lee T.L., Francis J.A. Internal stresses in a clad pressure vessel steel during post weld heat treatment and their relevance to underclad cracking. International Journal of Pressure Vessels and Piping. 2021;193:104448. https://doi.org/10.1016/j.ijpvp.2021.104448
19. Fang X.-Y., Zhang H.-N., Ma D.-W., Wu Z.-J., Huang W. Influence of welding residual stress on subsurface fatigue crack propagation of rail. Engineering Fracture Mechanics. 2022;271:108642. https://doi.org/10.1016/j.engfracmech.2022.108642
20. Kozlov E.V., Popova N.A., Kabanina O.V., Klimashin S.I., Gromov V.E. Evolution of Phase Composition, Defective Structure, Internal Stresses and Carbon Redistribution during Tempering of Cast Structural Steel. Novokuznetsk: SibSIU; 2007:177. (In Russ.).
21. Kassner M.E., Geantil P., Levine L.E. Long range internal stresses in single-phase crystalline materials. International Journal of Plasticity. 2013;45:44–60. https://doi.org/10.1016/j.ijplas.2012.10.003
22. Zhang Y., Yu T., Xu R., Thorborg J., Liu W., Tischler J., Godfrey A., Jensen D.J. Local residual stresses and microstructure within recrystallizing grains in iron. Materials Characterization. 2022;191:112113. https://doi.org/10.1016/j.matchar.2022.112113
23. Glezer A.M., Kozlov E.V., Koneva N.A., Popova N.A., Kurzina I.A. Plastic Deformation of Nanostructured Materials. Boca Raton, London, New York: CRC Press, Taylor & Francis Group; 2017:334. http://dx.doi.org/10.1201/9781315111964
24. Valiev R.Z., Zhilyaev A.P., Langdon T.G. Bulk Nanostructured Materials: Fundamentals and Applications. Hoboken: Wiley/TMS; 2014:440. https://doi.org/10.1002/9781118742679
25. Vinogradov A., Estrin Y. Analytical and numerical approaches to modelling severe plastic deformation. Progress in Materials Science. 2018;95:172–242. https://doi.org/10.1016/j.pmatsci.2018.02.001
26. Wilde G., Divinski S. Grain boundaries and diffusion phenomena in severely deformed materials. Materials Transactions. 2019;60(7):1302–1315. https://doi.org/10.2320/matertrans.MF201934
27. Burkin S.P., Shimov G.V., Andryukova E.A. Residual Stresses in Metal Products. Ekateriburg: izd. Ural’skogo universiteta; 2015:248. (In Russ.).
28. Handbook on Experimental Mechanics. 2nd ed. Kobayashi A. ed. VCH; 1993:1074.
29. Reynolds A.P., Tang W., Gnaupel-Herold T., Prask H. Structure, properties, and residual stress of 304L stainless steel friction stir welds. Scripta Materialia. 2003;48(9):1289–1294. https://doi.org/10.1016/S1359-6462(03)00024-1
30. Cihak U., Staron P., Clemens H., Homeyer J., Stockinger M., Tockner J. Characterization of residual stresses in turbine discs by neutron and high-energy X-ray diffraction and comparison to finite element modeling. Materials Science and Engineering: A. 2006;437(1):75–82. https://doi.org/10.1016/j.msea.2006.04.049
31. Withers P.J. Mapping residual and internal stress in materials by neutron diffraction. Comptes Rendus Physique. 2007; 8(7-8):806–820. https://doi.org/10.1016/j.crhy.2007.09.015
32. Withers P.J., Turski M., Edwards L., Bouchard P.J., Buttle D.J. Recent advances in residual stress measurement. International Journal of Pressure Vessels and Piping. 2008; 85(3):118–127. https://doi.org/10.1016/j.ijpvp.2007.10.007
33. Sekimoto K. Internal stress as a link between macroscale and mesoscale mechanics. In: Chemomechanical Instabilities in Responsive Materials. 2009:241–250. https://doi.org/10.1007/978-90-481-2993-5_10
34. Wong S.L., Dawson P.R. Evolution of the crystal stress distributions in face-centered polycrystals subjected to cyclic loading. Acta Materialia. 2011;59(18):6901–6916. https://doi.org/10.1016/j.actamat.2011.07.042
35. McNelis K.P., Dawson P.R., Miller M.P. A two-scale methodology for determining the residual stresses in polycrystalline solids using high energy X-ray diffraction data. Journal of the Mechanics and Physics of Solids. 2013;61(2):428–449. https://doi.org/10.1016/j.jmps.2012.09.015
36. Demir E., Park J.-S., Miller M.P., Dawson P.R. A computational framework for evaluating residual stress distributions from diffraction-based lattice strain data. Computer Methods in Applied Mechanics and Engineering. 2013;265:120–135. https://doi.org/10.1016/j.cma.2013.06.002
37. Skrotzki W. Deformation heterogeneities in equal channel angular pressing. Materials Transactions. 2019;60(7): 1331–1343. https://doi.org/10.2320/matertrans.MF201926
38. Yildirim C., Jessop C., Ahlström J., Detlefs C., Zhang Y. 3D mapping of orientation variation and local residual stress within individual grains of pearlitic steel using synchrotron dark field X-ray microscopy. Scripta Materialia. 2021;197:113783. https://doi.org/10.1016/j.scriptamat.2021.113783
39. Hirsch P.B., Howrie A., Nicholson R.B., Pashley D.W., Whelan M.J. Electron Microscopy of Thin Crystals. London: Butterworths; 1965:549.
40. Mader S., Zeeger A., Leitts K. Deformation hardening and dislocation distribution in HCC metals. In: Proceedings of the Conf. “Structure and Mechanical Properties of Metals”, Teddington, Middlesex, January 7 – 9, 1963. Moscow: Metallurgiya; 1967:9–41. (In Russ.).
41. Koneva N.A., Trishkina L.I., Zhdanov A.N., Perevalova O.B., Popova N.A., Kozlova E.V. Sources of stress fields in deformed polycrystals. Fizicheskaya mezomekhanika. 2006;9(3):93–102. (In Russ.).
42. Gromova A.V., Yur’ev A.B., Ivanov Yu.F., Chinokalov V.Ya. Formation of long-range stress fields during wire drawing. Izvestiya. Ferrous Metallurgy. 2006;49(2):27–31. (In Russ.).
43. Rybin V.V. Patterns of mesostructure formation during development of plastic deformation. Voprosy materialovedeniya. 2002;29(1):11–33. (In Russ.).
44. Calcaynotto M., Ponge D., Demir E., Raabe D. Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD. Materials Science and Engineering: A. 2010;527(10-11): 2738–2746. https://doi.org/10.1016/j.msea.2010.01.004
45. Kundu A., Field D.P. Influence of plastic deformation heterogeneity on development of geometrically necessary dislocation density in dual phase steel. Materials Science and Engineering: A. 2016;667:435–443. https://doi.org/10.1016/j.msea.2016.05.022
46.
47.
About the Authors
N. A. PopovaRussian Federation
Natal’ya A. Popova, Cand. Sci. (Eng.), Research Associate of the Scientific and Educational Laboratory “Nanomaterials and Nanotechnologies”
2 Solyanaya Sqr., Tomsk 634003, Russian Federation
E. L. Nikonenko
Russian Federation
Elena L. Nikonenko, Cand. Sci. (Phys.-Math.), Assist. Prof. of the Chair of Physics, Chemistry, Theoretical Mechanics, Tomsk State University of Architecture and Building; Senior Lecturer, National Research Tomsk Polytechnic University
2 Solyanaya Sqr., Tomsk 634003, Russian Federation
30 Lenina Ave., Tomsk, 634050, Russian Federation
M. A. Porfir’ev
Russian Federation
Mikhail A. Porfir’ev, Research Associate of Department of Scientific Researches
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
R. E. Kryukov
Russian Federation
Roman E. Kryukov, Dr. Sci. (Eng.), Assist. Prof. of the Chair of Ferrous Metallurgy
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
Review
For citations:
Popova N.A., Nikonenko E.L., Porfir’ev M.A., Kryukov R.E. Internal stresses and their sources in steels with BCC lattice. Izvestiya. Ferrous Metallurgy. 2024;67(2):161-175. https://doi.org/10.17073/0368-0797-2024-2-167-175