Контрольные карты Шухарта – простой, но не лёгкий для применения инструмент анализа данных

Все модели неверны,
Но некоторые полезны.
Джордж Бокс

Введение

Хорошо известно, что контрольные карты Шухарта (ККШ) – это основной инструмент анализа стабильности процессов, используемый практически во всех сферах человеческой деятельности. Они были изобретены Уолтером Шухартом, гением качества, почти 100 лет назад. Две знаменитые книги Шухарта вышли в 1931 и 1939 г. и были переизданы факсимиле Американским Обществом Качества в 1980 и 1986 г. [1; 2]. У. Деминг, друг и соратник Шухарта, написал краткое предисловие к изданию 1939 г., которое заканчивается следующими словами: «Возможно еще полстолетия пройдет, прежде чем вклад доктора Шухарта в систему образования, науку и промышленность будет полностью признан» [2]. В данной работе обсуждаются некоторые проблемы на пути к указанной Демингом цели. Прежде всего, кратко рассмотрим, насколько успешно ККШ распространяются по миру. Затем объясним, почему ККШ – это простой, но совсем не легкий для применения инструмент анализа данных. Для этого будут использованы ранее опубликованные работы авторов и только что полученные новые результаты. В конце будут изложены соображения по дальнейшим исследованиям.

Применение ККШ – текущее состояние

На первый взгляд с применением ККШ все хорошо. Они успешно используются практически повсеместно в различных отраслях (например, в металлургии, автомобильной промышленности, при производстве полупроводников, в авиации, сельском хозяйстве, государственных организациях, здравоохранении, образовании, и т. д.).

ККШ как один из методов статистического управления процессами (SPC) достаточно часто упоминается в литературных источниках [3 – 6], которые включают в себя как давно изданные книги, считающиеся классикой в области SPC, так и достаточно новые издания [7 – 10]. Есть и международные стандарты по ККШ, как, например, [11], и множество информационных страниц в Интернете с советами по применению ККШ.

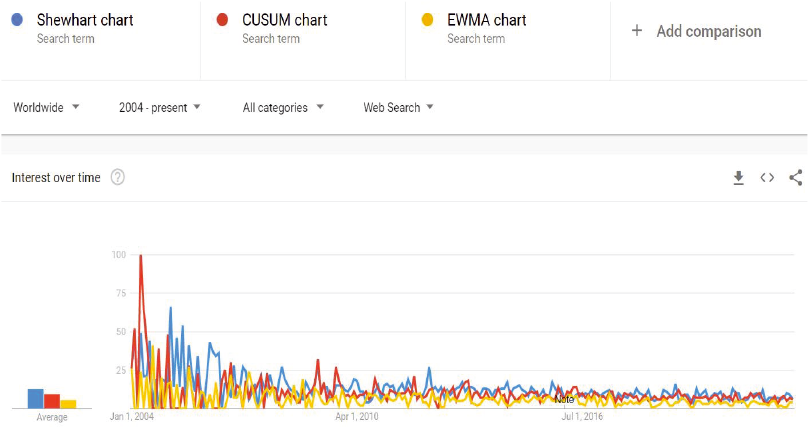
Тем не менее, существуют по меньшей мере две причины, не позволяющие сказать, что в области контрольных карт все в порядке. Первая проблема – это снижение интереса к ККШ среди статистиков и практиков. Об этом свидетельствуют данные, изображенные на рис. 1 и количество публикаций по теме в ведущих журналах. Именно этот вопрос недавно обсуждался в работе [12]. Частично это можно объяснить формально-бюрократическим внедрением ККШ, чего требуют некоторые международные стандарты. Другая проблема – явный недостаток новых исследований в области ККШ, выходящих за рамки традиционных моделей базовых контрольных карт. Речь идет не о разработке новых типов карт, которых и так появляется достаточно много. Имеется в виду расширение областей применения карт за пределы тех допущений, которые традиционно используются в теории ККШ. Вот некоторые редкие примеры таких исследований. В 2011 г. была опубликована работа «Особые причины вариаций и статистические модели: новый подход к старой теме» [13]. Авторы (один из которых является соавтором данной статьи) предложили разделить особые причины вариаций на те, которые вызваны вмешательством, имеющим ту же самую функцию распределения (ФР), что и исходный процесс, и те, которые порождены иной ФР. Первый подход использовался во всех предыдущих публикациях, второй показал, что результирующая оперативная характеристика (вероятность выхода точки за границы карты) может сильно отличаться от описанной во всех учебниках. В 2017 г. была опубликована работа [14], которая поднимала очень важный вопрос о значении порядка следования данных: на самом деле процессов со случайными данными почти не бывает, но вся существующая теория ККШ основана на предположении, что данные процесса полностью случайны. В 2021 г. появилась статья о влиянии кратковременного смещения среднего на поведение ККШ [15]. Было показано, что в условиях кратковременного смещения карта средних может потерять свое преимущество перед картой индивидуальных значений, что противоречит всем руководствам по SPC. Эти три примера – капля в море разнообразных возможностей расширения традиционного подхода к ККШ за счет расширения границ тех допущений, какие уже много десятилетий используются в стандартных моделях.

Настоящая работа продолжает расширять список условий, игнорируемых традиционно. На этот раз откажемся от обычного допущения о нормальном распределении параметров процесса и обсудим ряд последствий этого решения. Кроме того, рассмотрим различные типы особых причин вариабельности и их влияние на применение ККШ.

Влияние отсутствия нормального распределения параметров процесса на работу ККШ

Этот раздел состоит из двух частей. Сначала обсудим, всегда ли результаты измерений распределены нормально. Затем продемонстрируем, как меняются пределы ККШ, когда ФР ненормальна, и опишем наиболее удобный для практиков способ учета этого обстоятельства.

Всегда ли результаты измерений распределены нормально? Таково широко распространенное мнение многих авторов, книг и даже стандартов. Например, в стандарте [11] говорится следующее: «Применение контрольных карт для количественных данных предполагает в данном стандарте, что контролируемая характеристика подчиняется нормальному распределению (распределению Гаусса), причем отклонения от этого распределения влияют на эффективность карт. Коэффициенты, используемые для вычисления контрольных границ, выведены для нормального распределения характеристик. Поскольку обычно контрольные границы используют как эмпирические критерии при принятии решений, разумно малые отклонения от нормальности могут иметь место. В соответствии с центральной предельной теоремой, выборочные средние имеют распределение, приближающееся к нормальному, даже когда отдельные наблюдения не подчиняются нормальному закону. Это обосновывает возможность предположения о нормальности для X-карт даже при объемах выборок столь малых, как 4 или 5 единиц. Если использовать отдельные наблюдения для изучения возможностей процесса, истинное распределение важно. Распределения размахов и стандартных отклонений не являются нормальными, хотя предположение о нормальности использовано при определении коэффициентов для вычисления контрольных границ карт размаха и стандартного отклонения. Небольшие отклонения распределения характеристики процесса от нормального распределения не должны быть препятствием в использовании таких карт, как эмпирической процедуры принятия решений» (курсив авторов).

Но что такое «разумно малые отклонения от нормальности» или «небольшие отклонения»? Эти фразы не дают никакого операционального определения [16] того, какое изменение закона распределения следует считать существенным. Недавние результаты [17] позволили определить эти фразы операционально и дали возможность предложить алгоритм построения ККШ в условиях очевидного отсутствия нормальности ФР.

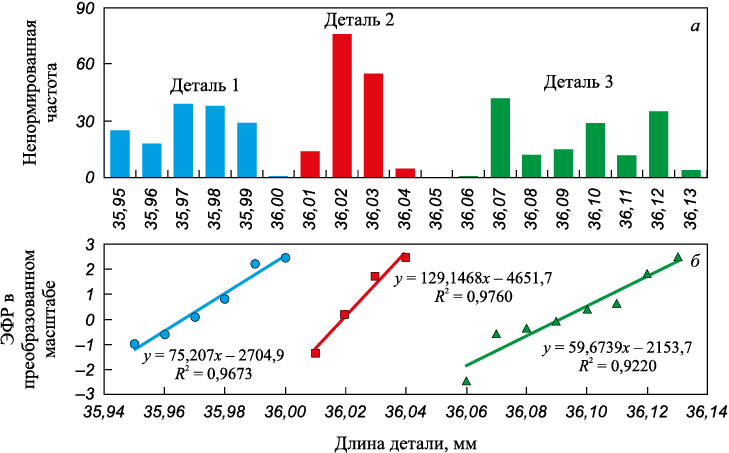
Одна из самых распространенных ошибок относительно универсальности нормального закона – мнение о том, что результаты измерений всегда распределены в соответствии с кривой Гаусса. Чтобы проверить эту гипотезу на практике, были взяты три детали и измерены каждая 150 раз одним и тем же инструментом. Результаты показаны на рис. 2. Все три детали взяты из одного процесса, но из разных точек интервала допуска. ККШ для деталей показали, что у первой и второй детали процессы стабильны, а у третьей число различимых категорий равно трем. Все гистограммы оказались явно ненормальными, и проверка гипотезы о нормальности с помощью процедуры, представленной в работе [18], подтвердила этот вывод. Таким образом, можно утверждать, что результаты повторных измерений могут не подчиняться нормальному закону, как и результаты измерения любых объектов.

Как отсутствие нормальности ФР влияет на коэффициенты ККШ? Существует множество процессов с ФР, заметно отличных от закона Гаусса. Как следует анализировать стабильность таких процессов, учитывая, что единственный инструмент определения стабилен ли процесс – это контрольная карта? Подробный обзор литературы и результаты моделирования асимметричных данных, полученные авторами, приведены в работе [17]. Здесь рассмотрены результаты сравнительного анализа ненормальных данных с помощью традиционного подхода и на базе предложенного в работе [17] алгоритма действий. Традиционный подход основан на процитированном выше утверждении из стандарта [11]. Однако, что скажут факты?

Для начала, были сгенерированы 400 выборок случайных чисел, подчиняющихся экспоненциальному распределению с параметром λ = 0,01 (каждая выборка состояла из 400 точек). Для этого с помощью Excel генерировали случайные числа из равномерной ФР и умножали их логарифмы на (–100), что и дало экспоненциально распределенную выборку данных.

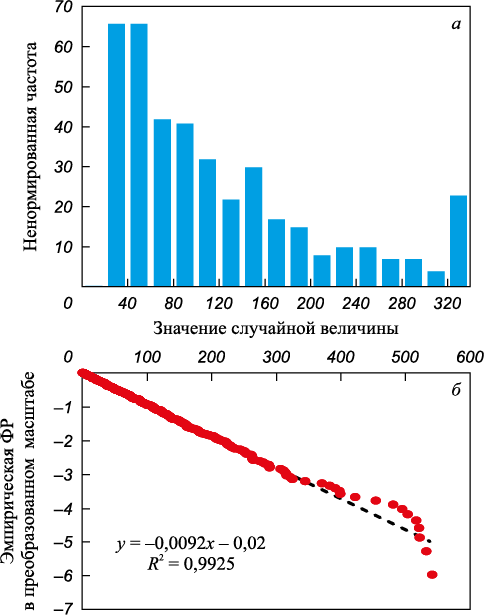
Гистограмма одной из полученных выборок показана на рис. 3, а. На рис. 3, б приведена эмпирическая ФР на вероятностной сетке экспоненциального распределения. Обе части рис. 3 демонстрируют, что распределение точек в выборке близко к экспоненциальному¹. Параметры описательной статистики: среднее = 105,5; стандартное отклонение = 105,0; асимметрия = 1,82; эксцесс = 3,78 (Внимание: Excel 2013 вычисляет избыточный эксцесс); минимальное значение = 0,51; максимальное = 541,4; медиана = 73,9; первая квартиль = 31,1; третья = 142,8; верхний предел жестких выбросов равен 477,87, что позволило выявить восемь точек жестких выбросов (ЖВ)² (они очевидны на рис. 3, б).

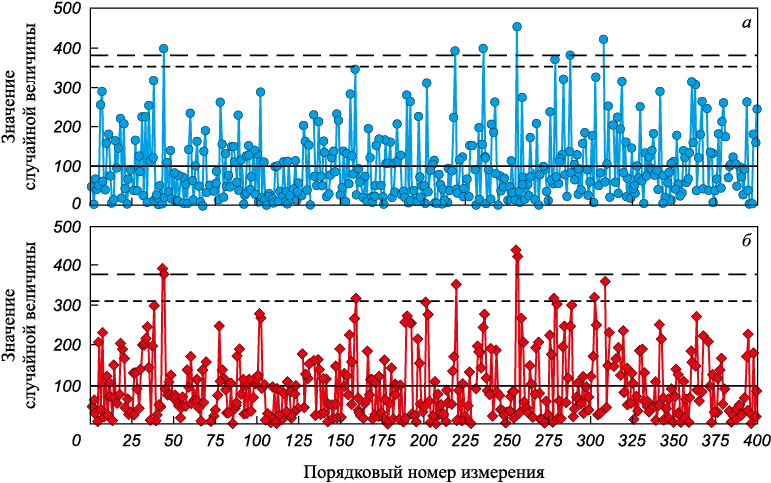
После исключения ЖВ была построена контрольная карта индивидуальных значений и скользящих размахов (x-mR), используя стандартные значения коэффициентов ККШ [19]: E₂ = 2,66; D₄ = 3,27. Полученная x-mR карта приведена на рис. 4. Контрольные пределы этой карты показаны пунктирными линиями. Процесс нестабилен, так как семь точек (1,8 % общего числа) на карте индивидуальных значений (x) и девять точек (2,2 %) на карте скользящих размахов (mR) лежат выше верхнего контрольного предела (ВКП). Однако, согласно результатам работы [17], для экспоненциальной ФР коэффициент d₂ должен быть равен 2,99 вместо 2,66. Рассчитанный по модифицированным коэффициентам предел показан на рис. 4 длинными штрихами. Видно, что теперь на карте x есть только шесть точек, лежащих выше ВКП. Аналогично на карте mR вместо девяти точек имеем только четыре – уменьшение числа сигналов почти вдвое. Таким образом, в данном случае число ложных сигналов уменьшилось на 14 % для карты индивидуальных значений и на 44 % для карты скользящих размахов. Если бы была использована карта не средних, а медиан, результаты были бы такими же.

В качестве второго примера в таблице приведены ежемесячные данные о числе нарушений технологии на большом горно-обогатительном комбинате.

Вопрос: повышенное значение в сентябре – это особая причина вариаций или нет? Или, другими словами, стабилен ли процесс?

Чтобы ответить на этот вопрос, нужно построить карту x-mR. При использовании традиционного подхода к построению ККШ получаем следующие параметры карты: центральная линия (ЦЛ) = 20,7; средний скользящий размах (ССР) = 13,2; ВКП = 55,7. Следовательно, сентябрьское значение лежит выше ВКП. Исходя из этого, можно утверждать, что процесс нестабилен и нужно искать причину вмешательства. Однако этот результат был получен в рамках традиционного похода. Оправдано ли его использование в данном случае?

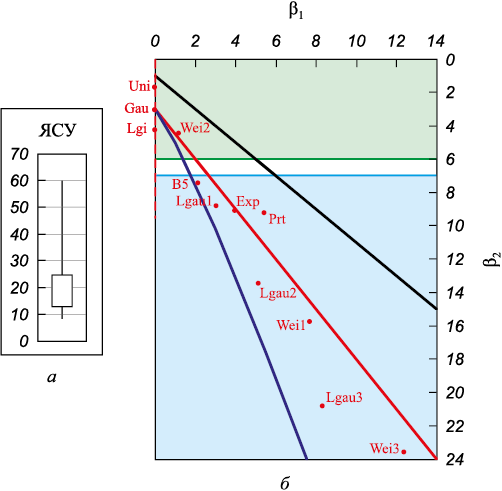
Поскольку объем выборки слишком мал, чтобы строить гистограмму, был построен ящик-с-усами (рис. 5). Из него видно, что данные явно асимметричны. Но значимо ли такое отличие от нормальности? Один из способов ответить на этот вопрос состоит в том, чтобы вычислить значения асимметрии и эксцесса. Excel дает значения 2,0 для асимметрии и 4,7 для эксцесса. Но Excel вычисляет избыточный эксцесс, так что реальное значение эксцесса равно 7,7. В работе [17] для значений эксцесса больше 7,0 в тех случаях, когда не известно, какая ФР соответствует нашим данным, предлагается брать значение коэффициента для ближайшей точки на плоскости кривых Пирсона (рис. 5, б). Для данных из таблицы ближайшая точка – это B5 (ФР Барра). Значение E₂ для этой ФР = 2,81 и скорректированный ВКП = 57,7 [17]. Следовательно, сентябрьское значение остается выше ВКП, и вывод о стабильности процесса не меняется. Но если бы, например, данные были ближе к экспоненциальному распределению (если бы эксцесс оказался вблизи значения 9), то тогда скорректированный коэффициент равнялся бы 2,99, скорректированный ВКП был бы равен 60,1 и процесс оказался бы стабильным (т. е. нет специальных причин вариации на карте).

Эти примеры демонстрируют важную черту ККШ, которую часто упускают многие авторы, и которая редко бывает понята практиками: контрольная карта Шухарта – это инструмент, требующий тесного взаимодействия человека и процесса. Построение ККШ не может быть полностью алгоритмизировано [20]. Правильное применение ККШ требует глубокого понимания специфики процесса и, одновременно, знания теории контрольных карт. Авторы уверены, что отсутст­вие такого симбиоза может быть главной причиной большого числа неудачных применений столь мощного инструмента на практике.

Некоторые мысли о стабильности процессов и сопутствующем анализе

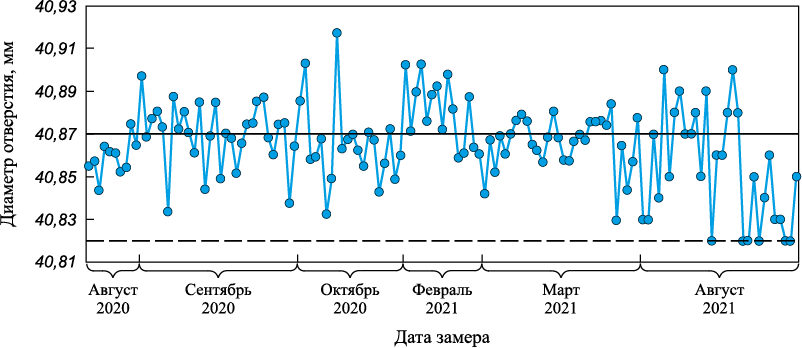
Как уже было отмечено выше, контрольная карта Шухарта – единственный инструмент определения стабильности процесса. Однако могут существовать различные типы нестабильности, которые требуют различной реакции. Рассмотрим процесс, показанный на рис. 6. Это реальный процесс с данными, полученными от одного из машиностроительных заводов РФ. Технология изготовления рассматриваемой детали была постоянна все время наблюдения. Система производства тоже не менялась. Из рис. 6 видно, что процесс производит детали, находящиеся внутри допусков (брак отсутствует), так что потребитель удовлетворен. Но что можно сказать о стабильности процесса? Обсудим ответ сначала с точки зрения инженера, малознакомого с процедурой SPC (будем называть его новичком), а затем с точки зрения опытного в методах SPC пользователя (эксперт).

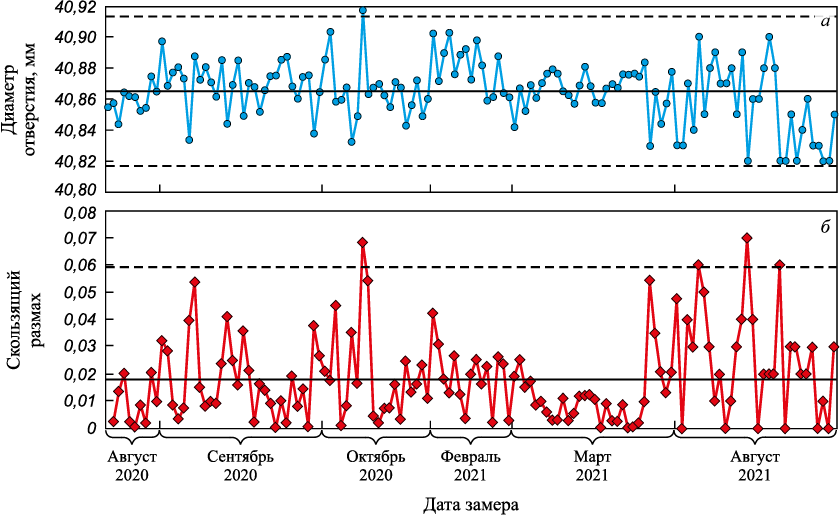
Новичок возьмет все данные без каких-либо сомнений и получит карту x-mR, показанную на рис. 7. ЦЛ будет равна 40,865, ВКП = 40,913, нижний контрольный предел (НКП) = 40,817. Эта карта говорит, что процесс нестабилен (одна точка над ВКП и четыре точки над ВКПсР на карте mR). Или процесс был стабилен в августе и сентябре 2021 г. и в марте 2022 г., но стал нестабилен в октябре 2021 г. и в марте 2022 г. Никаких проблем у новичка не возникнет и с расчетом индекса воспроизводимости процесса (ИВП): C_p будет равно 1,04 (0,1 делим на 6 сигм, сигма = (средний скользящий размах)/d₂). Значение C_p, равное 1,04, соответствует потенциальному уровню несоответствий (УН), равному 0,18 % или выходу годных (PY) = 99,82 %.

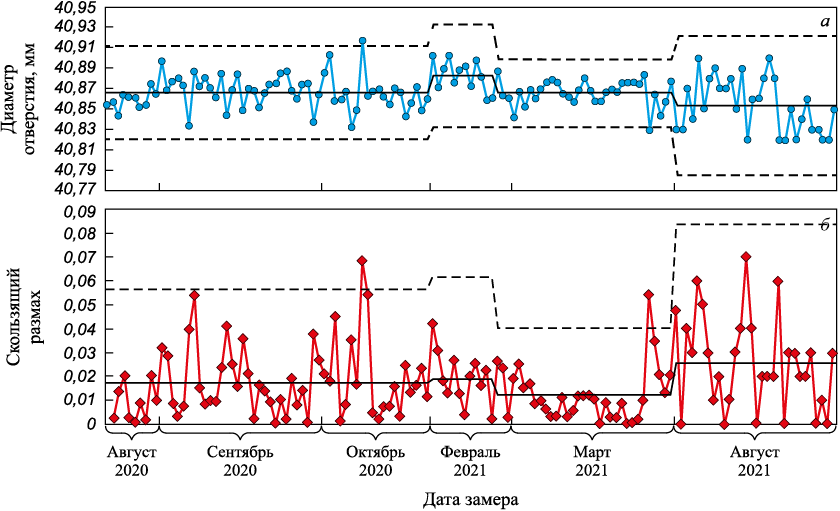
Эксперт скажет, что процесс явно неоднороден и его следует стратифицировать на однородные сегменты. Такая стратификация показана на рис. 8. Видны четыре участка с различными значениями ЦЛ и разными контрольными пределами:

Участок 1: август – октябрь 2020 г.

ЦЛ = 40,8665; ЦЛmR = 0,0173; ВКП = 40,9124; НКП = 40,8206; ВКПmR = 0,0564.

Участок 2: февраль 2021 г.

ЦЛ = 40,8830; ЦЛmR = 0,0189; ВКП = 40,9331; НКП = 40,8329; ВКПmR = 0,0616.

Участок 3: март 2021 г.

ЦЛ = 40,8662; ЦЛmR = 0,0123; ВКП = 40,8990; НКП = 40,8334; ВКПmR = 0,0403.

Участок 4: конец марта и август 2021 г.

ЦЛ = 40,8537; ЦЛmR = 0,0256; ВКП = 40,9218; НКП = 40,7856; ВКПmR = 0,0837.

Значения ИВП для каждого участка будут следующими: участок 1: C_p = 1,09; участок 2: C_p = 1,00; участок 3: C_p = 1,53; участок 4: C_p = 0,73. Если вычислить УН для каждого участка, то полученные значения будут меняться от 4,7 до 27 525 ppm. Разброс очень широкий, поэтому вопросы очевидны:

– какой способ анализа лучше подходит для совершенствования процесса;

– как следует интерпретировать стабильность такого процесса.

Начнем со второго вопроса.

Различные типы нестабильности процессов

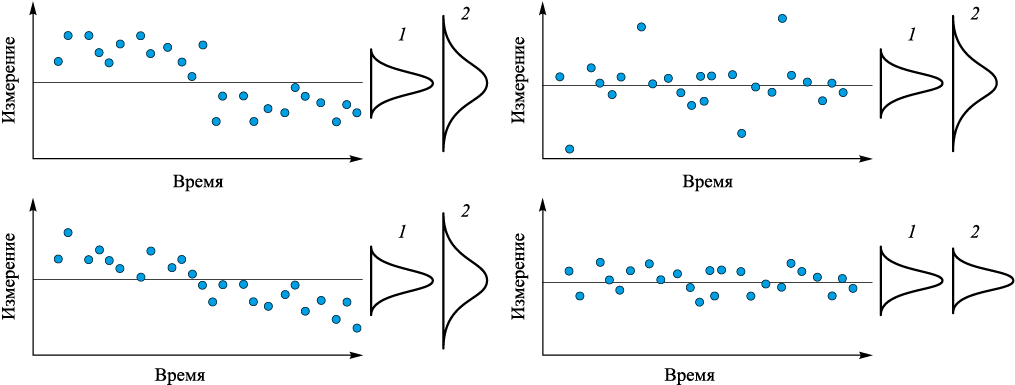
Представляется очевидным, что существуют разные типы нестабильности. Вот как обычный тип был описан доктором Демингом в предисловии к книге Шухарта 1939 г. [2]: «Главная задача контрольных карт – разделить рациональным образом вариацию на две составляющие: (1) собственно системную (доктор Шухарт называл это «случайными причинами»), ответственность менеджмента; и (2) особые причины, которые Деминг назвал «специальными», конкретные для некоторого эфемерного (мимолетного, непродолжительного) события, которые обычно можно выявить и устранить. Процесс находится в статистически управляемом состоянии, когда на него более не влияют специальные причины. Работа процесса, находящегося в статистически управляемом состоянии, предсказуема»³. Рис. 9 воспроизведен из работы [21], где авторы обсуждали различные типы особых причин вариаций, существующие в разных процессах. В трех из четырех картинок можно видеть скачок среднего процесса, выбросы и дрейф среднего. Однако только рисунок с выбросами соответствует «эфемерному событию», которое упоминал Деминг в вышеприведенной цитате. И это не только точка зрения Деминга. В работе [22] У. Вудал дает следующее определение: «Считается, что “общие причины” вариаций возникают благодаря внутренней природе процесса и не могут быть изменены без изменения самого процесса. “Особые причины” вариаций – это необычные удары (толчки, сотрясения) или другие нарушения (сбои, срывы), причины которых можно и нужно устранить».

Очевидно, две левые картинки на рис. 9 демонстрируют изменения процесса вследствие какой-то причины. Но как она называется? Общая или особая? Поскольку общие причины принято считать чем-то «постоянным» (именно этот термин использовал Шухарт в своих книгах [1; 2]) и внутренне присущим собственно процессу, то причины изменения процесса на рис. 9 слева следует считать особыми. Однако они явно отличаются от выбросов и других эфемерных (кратковременных) событий. Поэтому видится целесообразным ввести в рассмотрение различные типы особых (специальных) причин. В работе [13] авторы предложили ввести два типа особых причин вариаций. Слегка изменив формулировки работы [13], авторы предлагают следующие определения:

Определение 1. Особая причина вариаций типа I (Intrinsic внутренняя) не меняет систему, в которой работает процесс (например, не меняет тип основополагающей ФР). Как следствие, вполне естественно считать, что этот тип особых причин принадлежит системе (хотя это не есть необходимое условие).

Определение 2. Особая причина типа X (eXtrinsic – внешняя) изменяет систему, в которой работает процесс (например, изменяет тип основополагающей ФР). Как следствие, вполне естественно считать, что этот тип особой причины не принадлежит системе (хотя это тоже не есть необходимое условие).

Если научное сообщество согласится с предложением авторов, то разница между новичком и экспертом сведется к пониманию разницы между различными типами особых причин. В любом случае, рассматриваемый процесс нестабилен. Однако разные типы нестабильности отличаются друг от друга принципиально. Нестабильность типа I требует поиска коренных причин вмешательства внутри системы. Этот поиск должен осуществляться командой процесса, поскольку именно они досконально и лучше, чем кто-либо другой знают и процесс, и систему в целом. Нестабильность типа X требует поиска коренной причины вне системы. Доктор Деминг часто повторял: «Системой нужно управлять. Система не может управлять сама собой» [23]. Поиск коренных причин в этом случае должно выполнять высшее руководство, ответственное за систему в целом.

Какой вариант анализа более пригоден для улучшения процесса

Ответ понятен – это зависит от цели и состояния процесса. Оба подхода могут оказаться верными для одной ситуации и неверными для другой. Такое заключение возвращает к началу статьи. По сути, ККШ очень просты технически и совсем не просты для реального применения. Формулы, на которых основаны расчеты параметров карт, доступны ученику начальной школы. Однако правильное применение ККШ требует глубокого понимания как анализируемого процесса, так и хорошего знания многочисленных допущений и ограничений, используемых на практике. Кроме того, нужно уметь объединять знания из различных областей деятельности в своей практике. Вот почему возможно наилучший подход к правильному использованию ККШ – командная работа. Авторы согласны с выводом работы [12]: «Чтобы начать движение в сторону реализации мечты Г. Уэллса – “Статистическое мышление когда-нибудь станет такой же необходимостью, как умение читать и писать” – нужно начать внедрение идей статистического мышления в программу начальной школы». Это означает, что обучение базовым основам построения ККШ должно быть включено в школьную программу.

Выводы

Проанализировано текущее состояние дел в области применения ККШ и обнаружено, что несмотря на их повсеместное применение во всем мире, существует много проблем, препятствующих более эффективному использованию этого мощного инструмента на практике. Чтобы уменьшить число таких проблем, предлагается следующее:

– отказаться от допущения о нормальности данных при анализе измерительных систем;

– использовать новые константы при расчете контрольных пределов на ККШ, если данные процесса явно ненормальны;

– использовать новый подход при определении особых причин вариаций.

Эти идеи, при условии их внедрения, будут иметь глубокое влияние на применение ККШ практиками. Они позволят существенно уменьшить число ошибочных решений при анализе реальных данных, т. е. улучшить качество управления соответствующими процессами.

Возможно, самая далеко идущая идея, вытекающая из результатов исследования, может быть сформулирована следующим образом – правильное применение ККШ не может быть полностью алгоритмизировано. Такие операции, как выбор однородных участков процесса, выбор типа карты, выбор длительности фазы 1, выбор правильных коэффициентов для расчета контрольных пределов требуют глубокого знания специфики процесса и дополнительного анализа, например, ФР или порядка следования данных и др. Это знание не может быть встроено в статистические программы заранее, оно рождается в процессе взаимодействия человека, который управляет процессом, и, собственно, самим процессом.

Авторы надеются, что данная статья поможет продвижению простой мысли: контрольная карта Шухарта кажется очень простым инструментом SPC, но это впечатление обманчиво, так как она не может быть использована эффективно без глубокого понимания самого процесса и знания основ теории вариабельности.