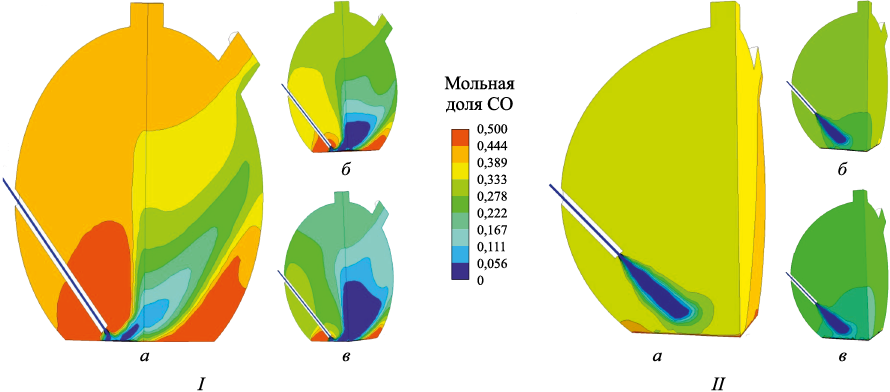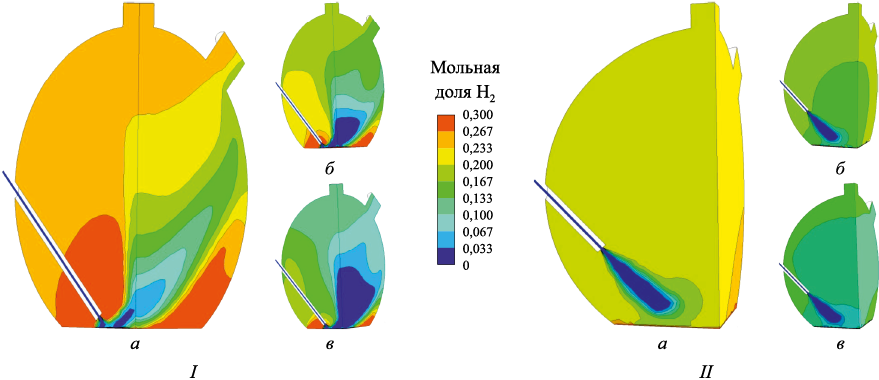Перейти к:
Математическое моделирование газодинамики и дожигания горючих компонентов над расплавом в плавильной печи-газификаторе
https://doi.org/10.17073/0368-0797-2024-1-112-120
Аннотация
Особенности организации технологического процесса и конструкции печи значительно влияют на параметры процессов дожигания, тем самым определяя необходимость построения математической модели зоны дожигания. В данном исследовании проведено моделирование газодинамики, химических реакций, конвективной диффузии и теплообмена в газовой среде над расплавом в экспериментальной плавильной печи-газификаторе при трех различных значениях расхода дутья и двух положениях фурм для дожигания. Получены распределения температур и концентраций продуктов дожигания. При нижнем расположении фурмы процесс дожигания осуществляется в области «отраженной» струи, образуются застойные зоны вокруг фурмы и между отраженной струей и поверхностью расплава, что ухудшает дожигание. При верхнем расположении фурмы дожигание происходит внутри первичной струи, осуществляется интенсивное перемешивание всех компонентов печной атмосферы и дожигание проходит более полно, что приводит к увеличению температуры отходящих газов при увеличении однородности полей температуры и концентраций по сравнению с нижним положением фурмы. Установлено, что при нижнем положении фурмы факел оказывается разомкнутым, его форма существенно зависит от расхода дутья, а объем с ростом расхода дутья увеличивается. При верхнем расположении фурмы факел является замкнутым, с увеличением расхода дутья его форма не изменяется, а объем уменьшается. Для процессов восстановления в шлаковом расплаве предпочтительно верхнее расположение фурмы, в то время как для получения генераторного газа с большим содержанием горючих компонентов на выходе из печи предпочтительно более близкое к поверхности расплава расположение фурмы.
Ключевые слова
Для цитирования:
Ерохов Т.В., Левицкий И.А., Подгородецкий Г.С., Горбунов В.Б. Математическое моделирование газодинамики и дожигания горючих компонентов над расплавом в плавильной печи-газификаторе. Известия высших учебных заведений. Черная Металлургия. 2024;67(1):112-120. https://doi.org/10.17073/0368-0797-2024-1-112-120
For citation:
Erokhov T.V., Levitskii I.A., Podgorodetskii G.S., Gorbunov V.B. Mathematical modeling of gas dynamics and off-gas post-combustion above the melt in a melter-gasifier furnace. Izvestiya. Ferrous Metallurgy. 2024;67(1):112-120. https://doi.org/10.17073/0368-0797-2024-1-112-120
Введение
Высокотемпературные печи с барботажным шлаковым слоем являются наиболее перспективными агрегатами для получения металлов из некондиционного сырья (труднообогатимых руд, железосодержащих отходов) и газификации углей, в том числе и низкосортных. Тепловой баланс процессов восстановления металлов и/или газификации низкосортных углей, протекающих в шлаковом расплаве, поддерживается возвратом тепла в шлаковую ванну от дожигания над шлаком СО и Н2 , образующихся, в свою очередь, в результате совокупности окислительно-восстановительных процессов в шлаковом слое [1 – 3].
Для анализа процессов, происходящих при дожигании газов в металлургических агрегатах, широко распространено математическое моделирование. Так, в работах [4 – 7] рассмотрены вопросы моделирования дожигания в дуговой сталеплавильной печи. Разработка моделей дожигания для кислородного конвертера описана в работе [8], а для его модификаций с донной продувкой инертным газом: AOD конвертера и KOBM конвертера в работах [9 – 11]. Ряд исследований посвящен изучению моделирования дожигания в агрегатах прямого восстановления железа [12 – 15]. Результаты этих работ показывают, что особенности организации технологического процесса и конструкции печи значительно влияют на параметры процессов дожигания, тем самым определяя необходимость построения математической модели зоны дожигания (зоны печи над расплавом) для печей типа Ромелт, печи Ванюкова или барботажных печей иной конструкции с наличием зоны дожигания отходящих газов.
Целью данного исследования является моделирование газодинамики, химических реакций, конвективной диффузии и теплообмена в газовой среде над расплавом в экспериментальной барботажной плавильной печи-газификаторе при различных значениях расхода дутья и положениях фурм для дожигания. Математическое моделирование осуществлялось в среде Ansys Fluent 15.0.7.
Постановка задачи
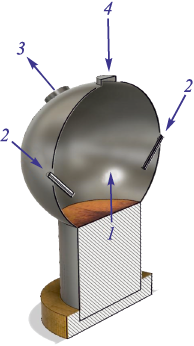
Геометрия рабочего пространства экспериментальной плавильной печи-газификатора схематически представлена на рис. 1.
Рис. 1. Схема экспериментальной плавильной печи-газификатора: |
При штатном режиме работы печи ее цилиндрическая часть 1 заполнена шлаковым расплавом, поверхность которого совпадает с границей цилиндрической и сферической частей. Химические реакции, проходящие в расплаве, происходят под действием дутья, подаваемого через боковые фурмы нижнего ряда (на схеме не показаны, в данной работе не исследуются). В результате этих процессов выделяются газы с высокой температурой, выходящие в надшлаковое пространство, где они дожигаются с помощью обогащенного кислородом дутья, которое подается через две фурмы 2 верхнего ряда, входящие в печь на уровне центра сферической части под углом 45°.
Газообразные продукты дожигания удаляются через два газоотвода 3 (плоскость осей газоотводов и плоскость осей фурм взаимоперпендикулярны).
Основные геометрические параметры конструкции, м, приведены ниже:
Диаметр сферической части печи 3,00
Диаметр цилиндрической части печи 1,80
Внутренний диаметр газоотвода 0,50
Внутренний диаметр входной трубы для сыпучих 0,40
Внутренний диаметр фурмы верхнего ряда 0,02
Внешний диаметр фурмы верхнего ряда 0,10
Основные допущения
Для облегчения расчетной процедуры не учитывалась передача теплоты через твердые стенки (как самой печи, так и фурм), что позволило исключить из рассмотрения области, заполненные твердыми веществами (стенки печи и фурм), ограничив учет их наличия тепловыми граничными условиями.
Поскольку работа посвящена изучению процессов, происходящих в надшлаковом пространстве печи, в качестве расчетной области рассматривалась только та часть рабочего пространства, которая заполнена газовой средой – шар со срезанным сегментом в нижней части и тремя примыкающими к нему небольшими цилиндрическими элементами в верхней части. Она имеет три входных сечения (поверхность расплава и входные сечения фурм дожигания) и два выходных (отверстия газоотводов – окно для подачи сыпучих считается закрытым крышкой).
Поскольку описанная геометрия обладает двумя плоскостями симметрии и не содержит элементов, закручивающих потоки, то и поля моделируемых величин обладают такой же симметрией, что позволяет взять в качестве расчетной области только четверть рабочего пространства, ограниченную плоскостями симметрии.
Соответственно, площади входных и выходных сечений в такой расчетной области станут меньше в 4 раза, и в такое же количество раз должны быть при моделировании уменьшены расходы во входных сечениях по сравнению с реальными.
Геометрия расчетной области была задана в приложении Design Modeler, генерация расчетной сетки и выбор сечений для задания граничных условий выполнены в приложении Ansys Meshing. Затем в приложении Fluent расчетная сетка была преобразована в полиэдрическую, что позволило улучшить показатель ортогональности граней ячеек и уменьшить погрешности, связанные с так называемой схемной диффузией.
При моделировании использованы следующие модели:
– модель диффузионно-конвективного переноса теплоты (решение уравнения энергии);
– k-ε модель турбулентности (в разновидности Realizable со стандартными пристеночными функциями);
– модель переноса компонентов (т. е. решение задачи конвективной диффузии) с учетом химических реакций, происходящих в объеме, причем взаимодействие кинетики и турбулентности принималось в соответствии с моделью Finite-Rate/Eddy-Dissipation.
Последняя из упомянутых моделей учитывает кинетику химических реакций, однако проверяет, какой из процессов – химическое взаимодействие или турбулентный перенос – является лимитирующим. В работах [16 – 19] эта модель применена для изучения горения метана, подаваемого в дутьевую фурму доменной печи.
В соответствии с этой моделью для каждого компонента смеси, заполняющей расчетную область, решается уравнение конвективной диффузии относительно его локальной массовой доли Yi в каждом узле расчетной сетки:
| \[\frac{\partial }{{\partial t}}\left( {{\rm{\rho }}{Y_i}} \right) + \vec \nabla \left( {{\rm{\rho \vec \omega }}{Y_i}} \right) = - \vec \nabla {\vec J_i} + {R_i},\] | (1) |
где ρ – плотность смеси, кг/м3; \({\rm{\vec \omega }}\) – вектор скорости, м/с; Ri – скорость образования i-го компонента в результате химических реакций, кг/(м3·с); \({\vec J_i}\) – плотность диффузионного потока i-го компонента, кг/(м2·с), которая зависит от градиентов концентрации этого компонента и температуры в соответствии с выражением
| \[{\vec J_i} = - \left( {{\rm{\rho }}{D_{i,m}} + \frac{{{{\rm{\mu }}_t}}}{{S{c_t}}}} \right)\vec \nabla {Y_i} - {D_{T,i}}\frac{{\vec \nabla T}}{T},\] | (2) |
где Di, m и DT, i – коэффициенты диффузии и термодиффузии (Соре) для i-го компонента смеси, м2/с, соответственно; Sct – турбулентное число Шмидта, равное по умолчанию 0,7 (\(S{c_t} = \frac{{{{\rm{\mu }}_t}}}{{{\rm{\rho }}{D_t}}},\) где μt – динамический коэффициент турбулентной вязкости, Па·с; Dt – коэффициент турбулентной диффузии, м2/с).
При участии компонента в нескольких реакциях величина Ri получается в результате сложения скоростей образования компонента по всем реакциям \({\hat R_{i,j}}\).
Считая (для упрощения) химические реакции необратимыми, можно записать j-ую реакцию в обобщенном виде следующим образом:
| \[\sum\limits_{i = 1}^N {{{\nu '}_{i,j}}} {{\rm M}_i}\sum\limits_{i = 1}^N {{{\nu ''}_{i,j}}} {{\rm M}_i},\] | (3) |
где N – количество химических компонентов в системе; \({\nu '_{i,j}}\) – стехиометрический коэффициент для i-го реагента в j-ой реакции; \({\nu ''_{i,j}}\) – стехиометрический коэффициент для i-го продукта в j-ой реакции; Mi – символ, обозначающий i-ый компонент; kf, i – константа скорости прямой реакции с номером j.
Для необратимых реакций молярная скорость образования/разрушения i-го компонента в j-ой реакции описывается выражением
| \[{\hat R_{i,j}} = ({{\rm{\nu ''}}_{i,j}} - {{\rm{\nu '}}_{i,j}})\left( {{k_{f,j}}\prod\limits_{l = 1}^N {{{\left[ {{C_{l,j}}} \right]}^{({{{\rm{\eta '}}}_{l,j}} + {{{\rm{\eta ''}}}_{l,j}})}}} } \right),\] | (4) |
где Cl, j – молярная концентрация l-го компонента в j-ой реакции, кмоль/м3; \({\eta '_{l,j}}\) – показатель скорости для l-го компонента в j-ой реакции; \({\eta ''_{l,j}}\) – показатель скорости для l-го продукта в j-ой реакции.
При этом константа прямой реакции с номером j вычисляется по формуле Аррениуса
| \[{k_{f,j}} = {A_j}{T^{{{\rm{\beta }}_j}}}{e^{ - \frac{{{E_j}}}{{RT}}}},\] | (5) |
где Aj – предэкспоненциальный показатель (в соответствующих единицах, зависящих от порядка реакции); βj – показатель степени для температуры (безразмерная величина); Ej – энергия активации для реакции (Дж/кмоль); R = 8,31 – универсальная газовая постоянная (Дж/(кмоль·К)).
В данном исследовании учитывали только две реакции горения – для водорода и монооксида углерода. Уравнения реакций и их параметры (частично взятые из базы данных Ansys Fluent) представлены в табл. 1.
Таблица 1. Значения кинетических констант для рассматриваемых реакций [20]
|
Во входных сечениях для дутья и горючих газов задавались температура, массовый расход и входные характеристики турбулентности (гидравлический диаметр и уровень турбулентных пульсаций), а в выходном сечении – разрежение, а также температура и характеристики турбулентности для внешней среды, примыкающей к выходному сечению (табл. 2).
Таблица 2. Граничные условия, задаваемые при расчете
|
Решение задачи осуществлялось в два этапа: сначала для решения уравнений газодинамики применяли метод SIMPLE, а для остальных уравнений – схемы первого порядка, затем продолжали расчет, используя сопряженный решатель для давления и импульса и схемы второго порядка для остальных переменных.
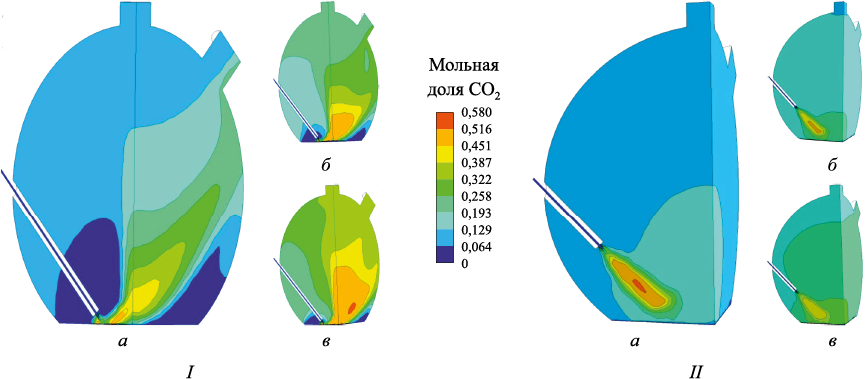
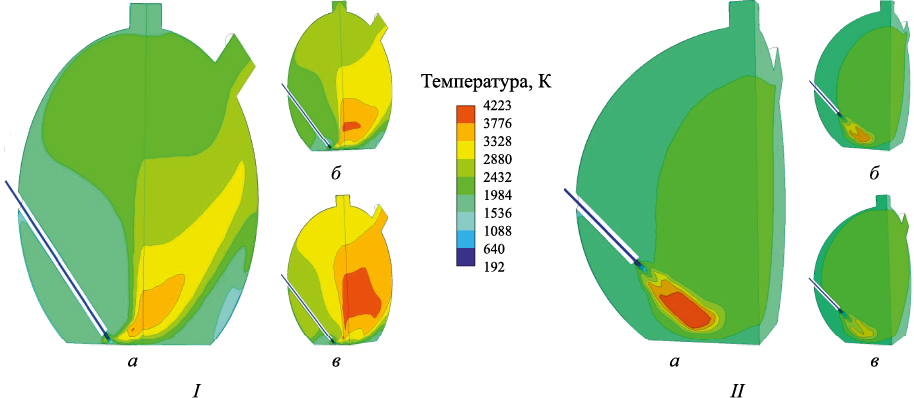
Результаты расчетов, представленные на рис. 2 – 5, получены для трех значений расхода дутья \(\dot M\)д: 0,03919 кг/с (а), 0,07838 кг/с (б), 0,11757 кг/с (в) (для получения истинных значений на полнообъемной модели их надо умножить на четыре) и двух положений фурмы относительно поверхности расплава: нижнего I (расстояние до поверхности расплава 0,1 м) и верхнего II (расстояние до поверхности расплава 0,7 м).
Рис. 2. Поле мольной доли CO для двух вариантов расположения фурмы (I, II)
Рис. 3. Поле мольной доли H2 для двух вариантов расположения фурмы (I, II)
Рис. 4. Поле мольной доли CO2 для двух вариантов расположения фурмы (I, II)
Рис. 5. Поле мольной доли H2O для двух вариантов расположения фурмы (I, II) |
Как видно из рис. 2 – 5, с увеличением расхода дутья концентрации дожигаемых компонентов (CO и H2 ) вполне предсказуемо уменьшаются, а концентрации продуктов (CO2 и H2O) закономерно возрастают. Однако при этом существенное влияние как на распределение компонентов, так и на достигаемые экстремальные значения их концентраций оказывает расположение фурмы.
При нижнем расположении фурмы «работает» фактически только «отраженная» от поверхности расплава струя дутья, внутри которой достигаются максимальные значения концентраций продуктов дожигания. Максимальные концентрации дожигаемых компонентов сохраняются в области, прилегающей к фурме выше сопла и в наиболее отдаленной от сопла области, прилегающей к поверхности расплава под «отраженной» струей.
Для варианта с поднятой фурмой происходит более интенсивное перемешивание дутья с остальными компонентами атмосферы надшлакового пространства, причем основная часть процессов перемешивания и дожигания происходит в области до столкновения струи с поверхностью расплава. Область максимальных концентраций продуктов дожигания образуется внутри первичной струи дутья, уже размываясь к поверхности расплава. При этом экстремальные значения этих концентраций менее выражены, чем при нижнем расположении фурмы, вследствие лучшего перемешивания и отсутствия застойных зон. Таким образом, при верхнем положении дутьевой фурмы достигается более полное дожигание, что подтверждается составом отходящих газов в выходных сечениях печи, а также характером температурного поля, полностью соответствующего полю концентрации продуктов сгорания (рис. 6). Из вышеизложенного следует, что при необходимости получения генераторного газа с большим содержанием горючих компонентов технологический процесс необходимо вести с нижним расположением фурмы, тогда как технологический процесс восстановления более эффективен при большей высоте расположения устья фурмы над расплавом.
Рис. 6. Температурное поле для двух вариантов расположения фурмы (I, II) |
Как видно на рис. 6, с увеличением расхода дутья размер высокотемпературной области для случая опущенной фурмы растет, а для случая поднятой – уменьшается.
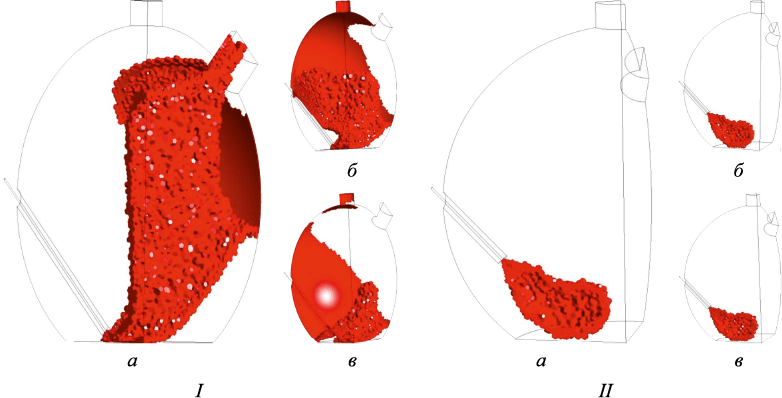
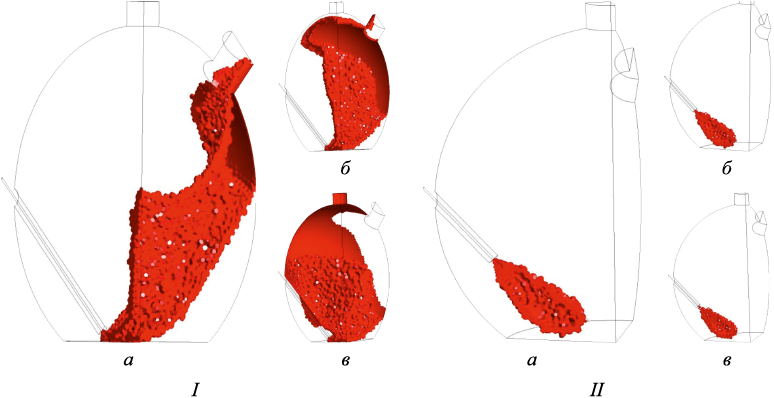
Ansys Fluent обладает инструментом для визуализации результатов расчета Isovolume, позволяющим строить трехмерные поверхности, соответствующие заданному значению какой-либо величины, поле которой вычисляется при решении задачи. Выбрав в качестве такой величины температуру, можно попытаться визуализировать такое понятие, как область факела. На рис. 7, 8 представлены изообъемы, построенные для температур 2200 и 2600 К соответственно.
Рис. 7. Изообъемы для температуры 2200 К при двух вариантах расположения фурмы (I, II)
Рис. 8. Изообъемы для температуры 2600 К при двух вариантах расположения фурмы (I, II) |
Как видно из представленных данных, для поднятой фурмы (фурмы в верхнем положении) факел является замкнутым, его форма с увеличением расхода не изменяется, а объем, ограниченный изоповерхностью, сокращается. Для нижнего положения фурмы увеличение расхода дутья существенно влияет на конфигурацию области струи, «отраженной» от поверхности расплава. При этом объем, ограниченный изоповерхностью, увеличивается – происходит более значительное рассеяние «отраженной» струи. Последнее дает избыточный тепловой поток на группу кессонов (охлаждаемых панелей), что является нежелательным явлением при ведении технологического процесса.
Выводы
В среде Ansys Fluent 15.0.7 численно исследован процесс дожигания в надшлаковом пространстве горючих компонентов (CO, H2 ), выделяющихся на поверхности ванны экспериментальной плавильной печи-газификатора. Изучено влияние расхода обогащенного кислородом дутья и положения фурм для его подачи на процесс дожигания (состав и температуру отходящих газов, конфигурацию факела, поля температуры и концентраций компонентов в атмосфере печи).
Установлено, что при нижнем расположении фурмы (расстояние от сопла до расплава 0,1 м) процесс дожигания осуществляется в области «отраженной» струи. Образуются застойные зоны вокруг фурмы и между отраженной струей и поверхностью расплава, что ухудшает дожигание. При верхнем расположении фурмы (расстояние от сопла до расплава 0,7 м) дожигание проходит внутри первичной струи, происходит интенсивное перемешивание всех компонентов печной атмосферы. Дожигание осуществляется более полно, что приводит к увеличению температуры отходящих газов при увеличении однородности полей температуры и концентраций по сравнению с нижним положением фурмы.
Установлено, что при нижнем положении фурмы факел оказывается разомкнутым, его форма существенно зависит от расхода дутья, а объем с ростом расхода дутья увеличивается. При верхнем расположении фурмы факел является замкнутым, с увеличением расхода дутья его форма не изменяется, а объем уменьшается.
Для процессов восстановления в шлаковом расплаве предпочтительно верхнее расположение фурмы, в то время как для получения генераторного газа с большим содержанием горючих компонентов на выходе из печи предпочтительно более близкое к поверхности расплава расположение фурмы (при котором, однако, существует опасность перегрева некоторых групп кессонов, что может негативно сказываться на состоянии конструкции печи и иных параметрах технологического процесса).
Список литературы
1. Роменец В.А., Валавин В.С., Усачев А.Б., Карабасов Ю.С. и др. Процесс Ромелт. Москва: МИСиС, ИД «Руда и Металлы»; 2005:400.
2. Баласанов А.В., Лехерзак В.Е., Роменец В.А., Усачев А.Б. Газификация угля в шлаковом расплаве. Москва: «Институт Стальпроект»; 2008:288.
3. Подгородецкий Г.С., Горбунов В.Б., Агапов Е.А., Ерохов Т.В., Козлова O.Н. Проблемы и перспективы утилизации золошлаковых отходов ТЭЦ. Часть 2. Известия вузов. Черная металлургия. 2018;61(7):557–563. https://doi.org/10.17073/0368-0797-2018-7-557-563
4. Li Y., Fruehan R.J. Computational fluid-dynamics simulation of postcombustion in the electric-arc furnace. Metallurgical and Materials Transactions B. 2003;34(3):333–343. https://doi.org/10.1007/s11663-003-0079-9
5. Arzpeyma N., Ersson M., Jönsson P.G. Mathematical modeling of postcombustion in an electric arc furnace (EAF). Metals. 2019;9(5):547. https://doi.org/10.3390/met9050547
6. Gruber J.C., Echterhof T., Pfeifer H. Investigation on the influence of the arc region on heat and mass transport in an EAF freeboard using numerical modeling. Steel Research International. 2016;87(1):15–28. https://doi.org/10.1002/srin.201400513
7. Tang X., Kirschen M., Abel M., Pfeifer H. Modelling of EAF off-gas post combustion in dedusting systems using CFD methods. Steel Research International. 2003;74(4):201–210. https://doi.org/10.1002/srin.200300182
8. Doh Y., Chapelle P., Jardy A., etc. Toward a full simulation of the basic oxygen furnace: Deformation of the bath free surface and coupled transfer processes associated with the post-combustion in the gas region. Metallurgical and Materials Transactions B. 2013;44(3):653–670. https://doi.org/10.1007/s11663-013-9817-9
9. Tang Y., Fabritius T., Härkki J. Mathematical modeling of the argon oxygen decarburization converter exhaust gas system at the reduction stage. Applied Mathematical Modelling. 2005;29(5):497–514. https://doi.org/10.1016/j.apm.2004.09.011
10. Song Z., Ersson M., Jönsson P. A study of post-combustion in an AOD flue. Steel Research International. 2014;85(7): 1173–1184. https://doi.org/10.1002/srin.201300307
11. Gou H., Irons G.A., Lu W.K. Mathematical modeling of postcombustion in a KOBM converter. Metallurgical and Materials Transactions B. 1993;24(1):179–188. https://doi.org/10.1007/BF02657884
12. Panjkovic V., Truelove J., Ostrovski O. Analysis of performance of an iron-bath reactor using computational fluid dynamics. Applied Mathematical Modelling. 2002;26(2): 203–221.https://doi.org/10.1016/S0307-904X(01)00056-7
13. Shin M.K., Lee S.D., Joo S.H., Yoon J.K. A numerical study on the combustion phenomena occurring at the post combustion stage in bath-type smelting reduction furnace. ISIJ International. 1993;33(3):369–375. https://doi.org/10.2355/isijinternational.33.369
14. Becker-Lemgau U., Tacke K.-H. Mathematical model for post combustion in smelting reduction. Steel Research. 1996;67(4):27–137. https://doi.org/10.1002/srin.199605469
15. Shinotake A., Takamoto Y. Combustion and heat transfer mechanism in iron bath smelting reduction furnace. Metallurgical Research & Technology. 1993;90(7–8):965–974. https://doi.org/10.1051/metal/199390070965
16. Левицкий И.А., Радюк А.Г., Титлянов А.Е., Сидорова Т.Ю. Влияние способа подачи природного газа на газодинамику и теплообмен в воздушной фурме доменной печи. Известия вузов. Черная металлургия. 2018;61(5):357–363. https://doi.org/10.17073/0368-0797-2018-5-357-363
17. Горбатюк С.М., Тарасов Ю.С., Левицкий И.А., Радюк А.Г., Титлянов А.Е. Влияние керамической вставки с завихрителем на газодинамику и теплообмен в воздушной фурме доменной печи. Известия вузов. Черная металлургия. 2019;62(5):337–344. https://doi.org/10.17073/0368-0797-2019-5-337-344
18. Албул С.В., Кобелев О.А., Радюк А.Г., Титлянов А.Е., Левицкий И.А. Влияние расхода и температуры природного газа на процессы, происходящие в воздушной фурме доменной печи с теплоизолирующей вставкой в дутьевом канале. Известия вузов. Черная металлургия. 2022;65(11):778–785. https://doi.org/10.17073/0368-0797-2022-11-778-785
19. Radyuk A.G., Gorbatyuk S.M., Tarasov Yu.S., Titlyanov A.E., Aleksakhin A.V. Improvements to mixing of natural gas and hot-air blast in the air tuyeres of blast furnaces with thermal insulation of the blast duct. Metallurgist. 2019;63(5–6):433–440. https://doi.org/10.1007/s11015-019-00843-6
20. Milewski J., Swirski K., Santarelli M., Leone P. Advanced Methods of Solid Oxide Fuel Cell Modeling. London, UK: Springer; 2011:201. https://doi.org/10.1007/978-0-85729-262-9
Об авторах
Т. В. ЕроховРоссия
Тимофей Витальевич Ерохов, ассистент кафедры энергоэффективных и ресурсосберегающих промышленных технологий
Россия, 119049, Москва, Ленинский пр., 4
И. А. Левицкий
Россия
Игорь Анисимович Левицкий, к.т.н., доцент кафедры энергоэффективных и ресурсосберегающих промышленных технологий
Россия, 119049, Москва, Ленинский пр., 4
Г. С. Подгородецкий
Россия
Геннадий Станиславович Подгородецкий, к.т.н.
Россия, 119049, Москва, Ленинский пр., 4
В. Б. Горбунов
Россия
Владислав Борисович Горбунов, к.т.н., Заместитель директора НОЦ «Инновационные металлургические технологии»
Россия, 119049, Москва, Ленинский пр., 4
Рецензия
Для цитирования:
Ерохов Т.В., Левицкий И.А., Подгородецкий Г.С., Горбунов В.Б. Математическое моделирование газодинамики и дожигания горючих компонентов над расплавом в плавильной печи-газификаторе. Известия высших учебных заведений. Черная Металлургия. 2024;67(1):112-120. https://doi.org/10.17073/0368-0797-2024-1-112-120
For citation:
Erokhov T.V., Levitskii I.A., Podgorodetskii G.S., Gorbunov V.B. Mathematical modeling of gas dynamics and off-gas post-combustion above the melt in a melter-gasifier furnace. Izvestiya. Ferrous Metallurgy. 2024;67(1):112-120. https://doi.org/10.17073/0368-0797-2024-1-112-120