Перейти к:
Параметрическая модель трехвалкового узла мини-стана радиально-сдвиговой прокатки
https://doi.org/10.17073/0368-0797-2023-3-376-386
Аннотация
В статье рассмотрены основные конструктивные особенности мини-станов радиально-сдвиговой прокатки (РСП), их наиболее распространенные типоразмеры. Описан обобщенный алгоритм проектирования таких станов с применением современных CAD систем. Перечислены основные подходы к методологии программного адаптивного проектирования моделей в инжиниринге, приведены их особенности и различия. В частности, рассмотрены методологии горизонтального моделирования, моделирования с явными ссылками и устойчивого моделирования. Описана методика виртуальных пережимов, приведена основная геометрическая схема пространственного положения валков продольного профиля. Полученные в результате расчетов данные закодированы и сведены в таблицы. Приведенные формулы использованы при параметрическом проектировании валкового узла трехвалкового стана РСП на примере типоразмера «30-70» в программной среде Autodesk Inventor. Полученная параметрическая модель, используя классические формулы методики виртуальных пережимов, позволяет автоматически перестраивать очаг деформации для новых исходных параметров. Разработанная модель применима для трехвалковых станов, имеющих углы раскатки рабочих валков δ = 5 – 15° и углы подачи β = 18 – 22°. Приведены эскизы и эпюры построенной модели для различных углов раскатки – 5, 10 и 15°. При увеличении угла раскатки заметно значительное увеличение конусности валка. Обозначен вектор будущих исследований по доработке и совершенствованию полученной программной модели. Дальнейшие исследования по доработке параметрической модели будут включать в себя расширение набора имеющихся параметров для добавления в компьютерную модель станины и валковых узлов, включая опоры, подушки, крышки, нажимное и уравновешивающее устройство и т. д.
Ключевые слова
Для цитирования:
Троицкий Д.В., Гамин Ю.В., Галкин С.П., Будников А.С. Параметрическая модель трехвалкового узла мини-стана радиально-сдвиговой прокатки. Известия высших учебных заведений. Черная Металлургия. 2023;66(3):376-386. https://doi.org/10.17073/0368-0797-2023-3-376-386
For citation:
Troitskii D.V., Gamin Yu.V., Galkin S.P., Budnikov A.S. Parametric model of a three-roll unit of radial-shear rolling mini-mill. Izvestiya. Ferrous Metallurgy. 2023;66(3):376-386. https://doi.org/10.17073/0368-0797-2023-3-376-386
Введение
Современные трехвалковые мини-станы радиально-сдвиговой прокатки (РСП) отличаются относительно простой схемой конструкции, основанной на рациональных углах подачи (18 – 22°) и раскатки (не более 10 – 12°) [1]. Как правило, они собираются под выпуск конкретного сортамента, который определяется типоразмерами стана и его конструктивными особенностями. При этом такое оборудование сохраняет разнообразие полноразмерных станов и обладает высокой мобильностью и компактностью. Мини-станы винтовой прокатки в достаточной степени соответствуют современным требованиям к бережливому производству [2] и позволяют использовать инновационные методы РСП, повышающие свойства материала в длинномерных объемах путем интенсивной пластической деформации [3; 4]. Так, например, для чистого магния показано значительное повышение механических свойств за счет изменения микроструктуры при трехвалковой винтовой прокатке [5]. В работах [6; 7] описано формирование градиентной структуры и повышение свойств для аустенитной нержавеющей стали AISI 321. Технологические возможности мини-станов РСП протестированы на титановых прутках на предмет соответствия требованиям нормативной документации (НМД) [8].
Например, существует трехвалковый прошивной мини-стан «30-80», предназначенный для горячей прошивки заготовок в гильзу с дном [9 – 11]. В качестве нажимного устройства использовано клиновое устройство, а валки имеют конструктивно заданные углы подачи и раскатки. Особенностью мини-стана является его мобильность, компактность и отсутствие необходимости монтажа на силовом фундаменте.
Также на большом количестве производственных предприятий и научных организаций успешно работают трехвалковые мини-станы винтовой прокатки типоразмера «14-40» [1; 12]. Подробный обзор основных конструкций и характеристик трехвалковых мини-станов РСП представлен авторами в работе [1]. Данные мини-станы нового типа отличают пониженная металлоемкость, достаточно низкие энергозатраты и значительная простота эксплуатации по сравнению с мелкосортными станами продольной прокатки, что делает их привлекательными для предприятий малого и среднего бизнеса, работающих в области металлургии и машиностроения.
Ранее авторами [13 – 15] разработан новый системный подход к созданию конструкций клетей на основе единой конструкторско-технологической системы «деформация металла – конструкция стана», обеспечивающей получение изделий с заданными характеристиками.
В основу новых конструкций клетей положены следующие принципы: использование станины закрытого типа, расположение рабочих валков при постоянных углах подачи и раскатки, вывод исполнительного механизма установки валков из-под прямого действия усилия прокатки. Это упростило не только конструкцию мини-стана, но и условия его эксплуатации.
Как правило, проектирование таких станов начинают от очага деформации, в котором задаются основные геометрические профили валков и прокатываемой заготовки. Учитывая большое количество существующих типоразмеров станов РСП, а также необходимость проектирования уникального оборудования под конкретный запрос заказчика, при проектировании целесообразно использовать возможности параметризации, которые существуют в большинстве современных CAD систем. Благодаря им можно значительно сократить затраченное время на проектирование компьютерных моделей, а также их последующий рефакторинг и исключение ошибок проектирования.
Современные CAD системы обладают большими встроенными возможностями по параметризации. Они позволяют создавать широкий набор параметров, которые могут быть статическими (как значение), расчетными (выраженные в виде математических формул, которые, в свою очередь, могут использовать статические параметры) или ссылочными (когда параметр ссылается на действительное значение имеющейся геометрии, чтобы быть использованным в иных геометрических узлах). CAD системы позволяют привязывать строящуюся геометрию к созданным параметрам любого вида и, таким образом, создавать семантические связи между узлами проектируемого оборудования.
Немаловажную роль при этом имеют выбор и использование подходящей методологии проектирования. Она позволяет выработать единый подход к построению ассоциативных связей и формированию параметрических зависимостей между отдельными узлами [16]. Это позволяет формализовать методы, используемые в параметрическом моделировании, приблизить дизайн к изначальному замыслу инженера [17], достичь стандартизации и внутренней согласованности программной модели; тем самым сократить затраченное на разработку время, а также максимизировать возможности по дальнейшему повторному использованию уже созданных ранее деталей и узлов. Использование подходящей и хорошо продуманной методологии позволяет изменять и вносить модификации в модели в значительно более короткий срок, чем при использовании неформального подхода [18; 19]. Развитие методологий проектирования напрямую связано с развитием CAD систем и их вовлечением в прикладные задачи инженерного дизайна. По большому счету, они представляют собой обобщенный инженерный опыт группы исследователей, нацеленный на увеличение гибкости и валидности проектируемых моделей [20]. Некорректная неформализованная методология негативно влияет на общее качество модели и затраченное на проектирования время [21]. Известны случаи, когда правильно выбранная методология, примененная в прикладной задаче MDO (Multidisciplinary design optimization – многопрофильная оптимизация дизайна), помогала добиться значительных результатов в авиастроении [22].
Существуют три известные формализованные методологии построения компьютерных моделей, которые ставят своими целями придание модели бóльшей гибкости для дальнейшего повторного использования и изменения, сокращение времени на разработку и модификацию, а также повышение общей устойчивости модели.
Методология горизонтального моделирования (The Horizontal Modeling Methodology) – это стратегия моделирования, запатентованная Delphi Technologies [23]. Она позволяет сократить количество критических ошибок, появляющихся в результате внесения изменений в модель за счет устранения зависимостей внутри имеющейся геометрии и параметров. Так, данные ошибки могут появляться в результате использования классической вертикальной древовидной структуры элементов, которая является неотъемлемой частью любой CAD системы. Вместо этого методология предлагает устранить/минимизировать количество таких зависимостей, а вместо них ссылаться на исходные элементы, неподверженные никаким изменениям – базовые плоскости и центр системы координат. Таким образом, вертикальная древовидная структура будет превращена в горизонтальную.
Методология моделирования с явными ссылками (The Explicit Reference Modelling – ERM) была предложена в работе [18]. Она призвана минимизировать количество зависимостей и ограничений в модели, связанных с текущей геометрией (которая склонна меняться под действием изменений всей модели), и заменить их ссылочными объектами, которые могут представлять собой или ссылаться на объекты вспомогательной геометрии. При этом, в отличие от методологии горизонтального моделирования, данная методология ставит перед собой задачу сохранения глобального замысла параметрического подхода.
Методология устойчивого моделирования [24] была предложена в работе [25] и фокусируется на создании устойчивых моделей с широкими возможностями повторного использования узлов и элементов. Она предлагает оптимизировать зависимости parent–child и структурировать древовидную структуру элементов более понятным образом.
Описанные методологии обладают своими преимуществами и недостатками, которые проявляются в зависимости от характера построенной модели. Основным критерием работоспособности параметрической модели является возможность адаптироваться к изменениям, внесенным в ее элементы. Работоспособность предложенных методологий проанализирована на примере различных сценариев оптимизации дизайна модели, включающей автоматическую генерацию большого количества геометрических вариаций и узлов [26].
В данной работе рассмотрено параметрическое моделирование валкового узла с использованием обобщенного алгоритма проектирования очага деформации трехвалкового стана РСП в программной среде Autodesk Inventor.
Постановка задачи и методы исследования
Геометрия пространственного положения валков продольного профиля
Для построения и расчета геометрии пространственного положения валков продольного профиля используется методика виртуальных пережимов, разработанная и предложенная для расчетов мини-станов РСП [13]. Данная методика основана на инвариантных соотношениях геометрии станов РСП с учетом изменения виртуальных углов подачи и раскатки вдоль оси очага деформации. Она позволяет выполнять эффективную параметризацию габаритных размеров валков и очага деформации [14]. Методика использует схему, представленную на рис. 1, а, где:
– З – рассматриваемое сечение заготовки радиусом rP с центром в точке О;
– В – сечение валка радиусом RP с центром в точке ОВ , контактирующее в точке F с сечением заготовки З;
– Ol и CL – оси прокатки (заготовки, очага деформации) и валка соответственно;
– GGB – общий перпендикуляр (эксцентриситет) длиной Е к осям валка и прокатки, т. е. \(\angle \)OGGB = \(\angle \)CGBG = 90°;
– ОС – перпендикуляр к оси прокатки длиной Р, пересекающий ось валка, т. е. \(\angle \)СOG = 90°. В станах барабанного типа лежит на оси барабана;
– β, δ, γ – углы подачи, раскатки и скрещивания соответственно.
Рис. 1. Схема взаимного расположения осей валка CL и прокатки Оl (a) |
Ряд используемых понятий – технологический пережим, геометрический пережим, конструктивная схема предложены в работах [27; 28]. Согласно методике, определение профиля валка по заданному профилю очага деформации сводится к расчету радиуса сечения валка, которое будет находиться в контакте с сечением заготовки известного радиуса ri и расположенным на известном расстоянии Δli по оси прокатки от технологического пережима (от точки О) (рис. 1, б).
Расчет калибровки валка по очагу деформации
Далее рассмотрим расчет по методике на примере определения радиуса валка в крайних сечениях очага деформации при исходных данных для стана типоразмера «30-70» (табл. 1). Диаметр валка в пережиме выбирается, исходя из возможности получения минимального калибра без пересечения поверхностей валков. Для определения максимально возможного диаметра валка в пережиме с учетом углов подачи, раскатки и зазора между валками существует формула [29]
| \[D_{\rm{в}}^{\max } = \frac{{d_{\rm{к}}^{\min } - \frac{\Delta }{{\cos \varphi }}}}{k},\] | (1) |
где \(D_{\rm{в}}^{\max }\) – максимально возможный диаметр валка в пережиме, мм; \(d_{\rm{к}}^{\min }\) – минимальный диаметр калибра в пережиме, мм; Δ – зазор между соседними валками, мм; φ – угол наклона образующей входного конуса валка, град.; k – коэффициент, связывающий диаметр валка с диаметром калибра.
Таблица 1. Исходные данные для примера расчета
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коэффициент связи k включает в себя такие параметры, как угол подачи β, раскатки δ, количество рабочих валков и может быть определен по формуле
| \[k = \frac{{\cos \delta - 0,87\sqrt {0,75\cos {\delta ^2} + 0,25\cos {\beta ^2}} }}{{\cos \delta \sqrt {0,57\cos {\delta ^2} + 0,19\cos {\beta ^2}} }}.\] | (2) |
В дальнейшем данное условие проверяется с помощью анализа интерференции тел в CAD системе.
Полученных в результате расчета данных достаточно для построения калибровки валков по трем сечениям. Результаты расчета сведены в табл. 2.
Таблица 2. Результаты расчета параметров калибровки по трем сечениям
| |||||||||||||||||||||||||||||||
Аналогичные расчеты калибровки валкового узла можно производить по большему количеству сечений для более высокой точности. Расчет каждого сечения в таком случае идентичен изложенному выше. По приведенному алгоритму возможно создать таблицу калибровки валка с требуемым шагом для нарезания на станках с числовым программным управлением.
Основные результаты исследования
В качестве основы для данного проектирования выбрана методология моделирования с явными ссылками. Все расчетные параметры из табл. 1 и 2 внесены в качестве пользовательских параметров в модели Autodesk Inventor. Данные параметры являются расчетными и определяются напрямую в программной среде Autodesk Inventor.
Все использованные параметры закодированы в переменные из двух символов (латинская буква и цифра), что позволяет значительно облегчить процедуру расчета в программной среде Autodesk Inventor:
– параметры X используются в качестве основных исходных данных для расчета модели;
– параметры A используются для определения параметров технологического и геометрического пережимов;
– параметры B используются для определения параметров виртуального пережима в сечении 1 входа в очаг деформации;
– параметры C используются для определения параметров виртуального пережима в сечении 2 выхода из очага деформации.
Полный перечень параметров представлен в табл. 3.
Таблица 3. Таблица кодирования параметров
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Для проверки корректности построенной модели используются параметры X1, X2, A2, B5, B6, C5 и C7. Для них справедливо отношение
| cosX1 cosX2 = cosB5 cosB6 = cosC5 cosC7 = cosA2. | (3) |
Для построения очага деформации в программной модели используется 3D-эскиз. Явные параметры этого эскиза при этом ссылаются на созданные пользовательские параметры. При корректно выстроенных зависимостях и заполненных исходных данных (X) модель будет иметь 0 степеней свободы на 3D-эскизе, т. е. построенный вариант геометрии является единственным возможным при заданных параметрах. Удаление какого-либо из исходных параметров (X) будет добавлять модели очага степени свободы.
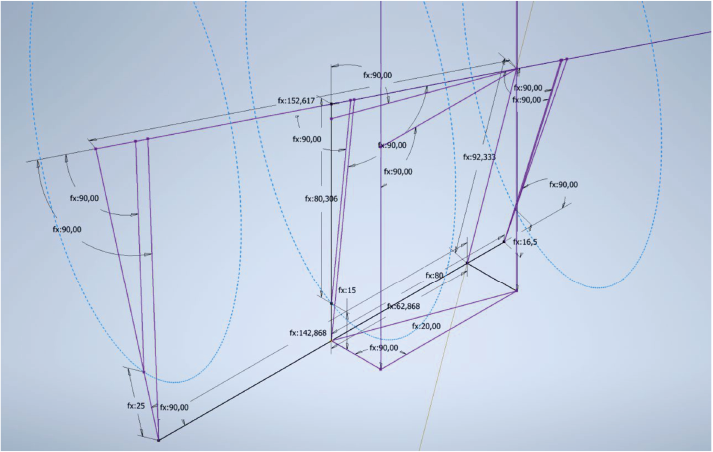
Построенная схема взаимного положения осей валка и прокатки представлена на рис. 2.
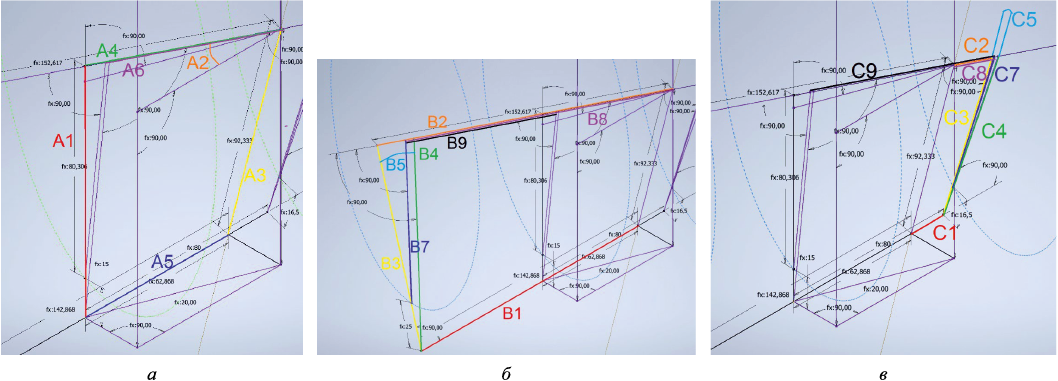
На рис. 3 представлены параметры A, B, C, используемые для построения геометрического и технологического пережимов валка.
Рис. 2. Адаптивная схема взаимного положения осей валка и прокатки (β = 20°, δ = 5°)
Рис. 3. Параметры, используемые для построения геометрических пережимов: А (а); В (б); С (в) |
Построение очага деформации в системе происходит от технологического пережима на оси прокатки, который является общим центром координат модели O. Далее следует провести ось прокатки, проходящую через центр координат модели. По ней определяется расстояние l между технологическим и геометрическим пережимами по оси прокатки (параметр A5), чтобы получить отрезок OG. От точки O, в свою очередь, проводится вспомогательная прямая, перпендикулярная отрезку OG. По ней от точки O последовательно откладывается радиус прутка в пережиме rP и радиус валка в пережиме RP (параметры X4 и X3 соответственно), чтобы получить точку C. Отрезок CGB (А4) в таком случае будет совпадать с осью валка. После этого с помощью перпендикуляров от отрезка OG следует построить угол подачи β (параметр X1). Далее проводится вспомогательная прямая из вершины угла β и параллельная отрезку ОС. После этого получаем точку GB , проведя эксцентриситет E (параметр А3) от точки G до пересечения с построенной вспомогательной прямой. Остальные виртуальные пережимы строятся аналогичным образом.
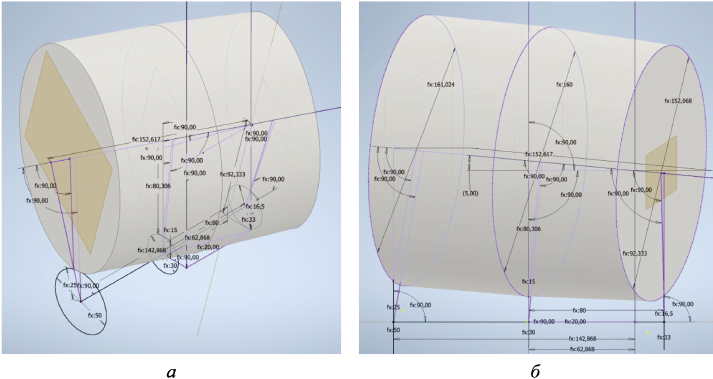
На рис. 4 – 6 представлены модели построенного валка-бочки для разных типоразмеров станов с помощью параметрической модели.
Рис. 4. Адаптивная модель построенного валка-бочки типоразмера «30-70» с углом раскатки δ = 5°:
Рис. 5. Адаптивная модель построенного валка-бочки типоразмера «30-70» с углом раскатки δ = 10°:
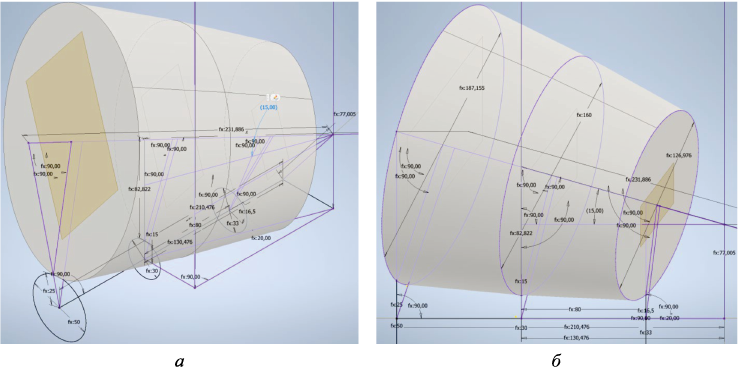
Рис. 6. Адаптивная модель построенного валка-бочки типоразмера «30-70» с углом раскатки δ = 15°: |
Полученный в результате проектирования очаг деформации и валок могут использоваться для построения трехвалкового узла мини-стана и моделей детали валка. Разработанная модель применима для трехвалковых станов, имеющих углы раскатки рабочих валков δ = 5 ÷ 15° и углы подачи β = 18 ÷ 22°.
Особенностями таких моделей являются быстрое построение и перестроение валковых соединений с помощью параметризации. Используя универсальные модульные соединения между отдельными параметрами каждой модели и узлами мини-стана, можно значительно сократить затраченное на проектирование стана время. Построенная модель при этом будет обладать достаточными критериями для качественного выпуска продукции требуемого сортамента, от которой зависят исходные параметры модели X.
На рис. 7 представлен очаг деформации, составленный из трех валков. Очаг деформации можно получить с помощью кругового массива, или создав сборку, позиционируя валки вокруг эскиза прокатываемого прутка под углом 120° и на заданный угол раскатки и подачи.
Рис. 7. Параметрическая модель очага деформации: валковое соединение, построенное с помощью метода параметризации (а); очаг деформации, полученный массивом круговых элементов (б) |
Метод параметризации способствует ускорению проектирования валковых соединений и прокатных станов, сокращая трудозатраты инженера на ручную корректировку деталей и отношений между узлами.
Выводы
Применение параметризируемого алгоритма проектирования значительно облегчает задачу инженера по созданию компьютерной модели. Так, метод построения очага деформации в зависимости от радиусов прокатываемой заготовки, валка, угла подачи и угла раскатки позволяет оперативно получить трехмерную модель калибровки валка и очаг деформации, на основании которого далее можно подобрать остальные конструктивные узлы стана.
Разработан алгоритм проектирования очага деформации в зависимости от настраиваемых параметров, которые используются при параметризации в CAD системе. В основе алгоритма заложена методика виртуальных пережимов, которая позволяет использовать инвариантные соотношения геометрии валков РСП применительно к требуемым параметрам технологического пережима – диаметрам валка и прутка, углам подачи и раскатки вдоль оси прокатки и/или оси валка.
Методология моделирования с явными ссылками использована при создании компьютерной модели валкового соединения стана типоразмера «30-70» с параметризируемыми характеристиками, которые можно изменять в зависимости от целевого назначения стана и выбранной конструкции. Построенная модель является адаптивной и позволяет быстро определять габаритные размеры и пространственное положение валков и очага деформации мини-стана.
Дальнейшая работа будет направлена на разработку адаптивной параметрической модели, включающей сборочный узел валковых узлов (вал и бочка рабочего валка, подшипниковые опоры, подушки), нажимное устройство и станины.
Список литературы
1. Галкин С.П., Гамин Ю.В., Алещенко А.С., Романцев Б.А. Современное развитие элементов теории, технологии и мини-станов радиально-сдвиговой прокатки. Черные металлы. 2021;(12). https://doi.org/10.17580/chm.2021.12.09
2. Галкин С.П. Технология и мини-станы радиально-сдвиговой прокатки – оптимальная техника для создания бережливого производства. Сталь. 2014;(1):39–42.
3. Naizabekov A., Lezhnev S., Arbuz A., Panin E., Koinov T. Simulation of radial-shear rolling of austenitic stainless steel AISI-321. Journal of Chemical Technology and Metallurgy. 2019;54(5):1086–1094.
4. Arbuz A., Kawalek A., Ozhmegov K., Panin E., Magzhanov M., Lutchenko N., Yurchenko V. Obtaining an equiaxed ultrafine-grained state of the longlength bulk zirconium alloy bars by extralarge shear deformations with a vortex metal flow. Materials. 2023;16(3):1062. https://doi.org/10.3390/ma16031062
5. Mashekov S., Smailova G., Alshynova A., Uderbayeva A., Sembaev N., Zhauyt A. Structure formation of aluminum alloy D16 while rolling bars in the radial shear mill. Metalurgija. 2020;59(2):195–198.
6. Diez M., Kim H.-E., Serebryany V., Dobatkin S., Estrin Y. Improving the mechanical properties of pure magnesium by three-roll planetary milling. Materials Science and Engineering: A. 2014;612:287–292. https://doi.org/10.1016/j.msea.2014.06.061
7. Naizabekov A., Lezhnev S., Panin E. Formation of a gradient structure in austenitic stainless steel AISI 321 by radial-shear rolling. Solid State Phenomena. 2021;316:246–251. https://doi.org/10.4028/www.scientific.net/ssp.316.246
8. Негодин Д.А., Галкин С.П., Харитонов Е.А., Карпов Б.В., Харьковский Д.Н., Дубовицкая И.А., Патрин П.В. Тестирование технологии радиально-сдвиговой прокатки и предпроектный выбор мини-станов для гибкого производства титановых прутков малых сечений в условиях АО ЧМЗ. Металлург. 2018;(11):40–46.
9. Mishin I., Naydenkin E., Ratochka I., Lykova O., Vinokurov V., Manisheva A. Effect of radial shear rolling and aging on the structure and mechanical properties of titanium alloy VT35. AIP Conference Proceedings. 2020;2310(1):020206. https://doi.org/10.1063/5.0034081
10. Shatalov R., Medvedev V., Bogdanov S. Development and use of an electromagnetic unit for controlling the mechanical properties along the steel vessel height at the exit from a rolling–pressing line. Russian Metallurgy (Metally). 2022;2022(6):628–633. https://doi.org/10.1134/S0036029522060210
11. Shatalov R., Medvedev V. Effect of deformed workpiece temperature inhomogeneity on mechanical properties of thin-walled steel vessels during treatment in a rolling and pressing line. Metallurgist. 2019;63(1–2):176–182. https://doi.org/10.1007/s11015-019-00807-w
12. Stefanik A., Szota P., Mróz S. Analysis of the effect of rolling speed on the capability to produce bimodal-structure AZ31 alloy bars in the three-high skew rolling mill. Archives of Metallurgy and Materials. 2020;65(1):329–335. https://doi.org/10.24425/amm.2020.131734
13. Галкин С.П., Фадеев В.А., Гусак А.Ю. Методика виртуальных пережимов для расчета мини-станов радиально-сдвиговой (винтовой) прокатки. Производство проката. 2016;(2):27–35.
14. Галкин С.П., Фадеев В.А., Гусак А.Ю. Сопоставительный анализ геометрии мини-станов радиально-сдвиговой (винтовой) прокатки. Производство проката. 2015;(12):19–25.
15. Белевич А.В., Гончарук А.В., Даева Е., Романцев Б.А. Исследование технологических и конструктивных параметров рабочих клетей винтовой прокатки с помощью современных конечно-элементных систем. Известия вузов. Черная металлургия. 2002;45(9):32–35.
16. Company P., Naya F., Contero M., Camba D.J. On the role of geometric constraints to support design intent communication and model reusability. Computer-Aided Design & Applications. 2020;17(1):61–76. https://doi.org/10.14733/cadaps.2020.61-76
17. Otey J., Company P., Contero M, Camba D.J. Revisiting the design intent concept in the context of mechanical CAD education. Computer-Aided Design & Applications. 2018;15(1):47–60. https://doi.org/10.1080/16864360.2017.1353733
18. Bodein Y., Rose B., Caillaud E. Explicit reference modeling methodology in parametric CAD system. Computers in Industry. 2014;65(1):136–147. https://doi.org/10.1016/j.compind.2013.08.004
19. Camba J.D., Contero M., Company P. Parametric CAD modeling: An analysis of strategies for design reusability. Computer-Aided Design. 2016;74:18–31. https://doi.org/10.1016/j.cad.2016.01.003
20. Cheng Z., Ma Y. A functional feature modeling method. Advanced Engineering Informatics. 2017;33:1–15. https://doi.org/10.1016/j.aei.2017.04.003
21. Aranburu A., Justel D., Contero M., Camba J.D. Geometric variability in parametric 3D models: Implications for engineering design. Procedia CIRP. 2022;109:383–388. https://doi.org/10.1016/j.procir.2022.05.266
22. Amadori K., Tarkian M., Ölvander J., Krus P. Flexible and robust CAD models for design automation. Advanced Engineering Informatics. 2012;26(2):180–195. https://doi.org/10.1016/j.aei.2012.01.004
23. Landers D.M., Khurana P. Horizontally-structured CAD/CAM modeling for virtual concurrent product and process design. Patent no. US6775581B2 USA. 10.08.2004.
24. Resilient Modeling Strategy. 2018; URL: https://www.resilientmodeling.net (Дата обращения: 15.12.2022)
25. Gebhard R. A resilient modeling strategy. Solid Edge University 2013. Siemens; 2013.
26. Aranburu A., Cotillas J., Justel D., Contero D., Camba D.J. How does the modeling strategy influence design optimization and the automatic generation of parametric geometry variations? Computer-Aided Design. 2022;151:103364. https://doi.org/10.1016/j.cad.2022.103364
27. Миронов Ю.М. Геометрические параметры процесса косой прокатки. Производство труб. 1962;(6):37–46.
28. Тетерин П.К. Теория поперечно-винтовой прокатки. Москва: Металлургия; 1971:386.
29. Будников А.С. Совершенствование процессов раскатки и калибрования труб в трехвалковых станах винтовой прокатки: Дисс. … канд. техн. наук. Москва: 2020:147.
Об авторах
Д. В. ТроицкийРоссия
Даниил Владимирович Троицкий, аспирант кафедры «Обработка металлов давлением»
Россия, 119049, Москва, Ленинский пр., 4
Ю. В. Гамин
Россия
Юрий Владимирович Гамин, к.т.н., доцент кафедры «Обработка металлов давлением»
Россия, 119049, Москва, Ленинский пр., 4
С. П. Галкин
Россия
Сергей Павлович Галкин, д.т.н., профессор кафедры «Обработка металлов давлением»
Россия, 119049, Москва, Ленинский пр., 4
А. С. Будников
Россия
Алексей Сергеевич Будников, к.т.н., доцент кафедры «Обработка металлов давлением»
Россия, 119049, Москва, Ленинский пр., 4
Рецензия
Для цитирования:
Троицкий Д.В., Гамин Ю.В., Галкин С.П., Будников А.С. Параметрическая модель трехвалкового узла мини-стана радиально-сдвиговой прокатки. Известия высших учебных заведений. Черная Металлургия. 2023;66(3):376-386. https://doi.org/10.17073/0368-0797-2023-3-376-386
For citation:
Troitskii D.V., Gamin Yu.V., Galkin S.P., Budnikov A.S. Parametric model of a three-roll unit of radial-shear rolling mini-mill. Izvestiya. Ferrous Metallurgy. 2023;66(3):376-386. https://doi.org/10.17073/0368-0797-2023-3-376-386