Перейти к:
Исследование теплового режима рабочих валков стана горячей прокатки с целью повышения точности расчета температур поверхностей их бочек
https://doi.org/10.17073/0368-0797-2023-3-283-289
Аннотация
Тепловой режим бочки рабочего валка непрерывного стана горячей прокатки – значимый фактор технологии, который влияет на качество формы стальной полосы, ее поперечное сечение, стойкость рабочих валков. Достоверный расчет параметров температурного режима позволяет определить форму теплового профиля и наилучшую профилировку поверхности бочки валка, добиться уменьшения дефектов планшетности готового проката. Наиболее распространенной является балансная модель теплового режима валка, точность которой в значительной степени определяется теплофизическими постоянными, в частности коэффициентами теплообмена валков: контактного – с полосой и конвективного – с охлаждающей водой. Имеются различные сведения о значениях и методах расчета этих коэффициентов, но большинство из них не учитывают наличие пауз в ритме прокатки чистовой группы клетей, длительность которых значительна. Отсутствие учета этого фактора влечет за собой существенные ошибки в расчетах теплового режима бочки валка. Проведен пассивный эксперимент, в ходе которого с помощью термопары измерены температуры поверхностей бочек рабочих валков в нескольких точках по их длине сразу же после вывалки. Также определены параметры прокатки стальных полос перед перевалкой: коэффициенты ритма прокатки, обжатия полосы в клетях, расходы воды на охлаждение валков и некоторые другие параметры. В результате получено эмпирическое уравнение для расчета коэффициента контактного теплообмена, учитывающее основные факторы технологии, в том числе длительность пауз в ритме прокатки. Использование уточненных коэффициентов для расчета температур бочки валка значительно повысило точность прогнозирования теплового режима, в частности теплового профиля рабочего валка, по значениям параметров прокатки.
Ключевые слова
Для цитирования:
Шалаевский Д.Л. Исследование теплового режима рабочих валков стана горячей прокатки с целью повышения точности расчета температур поверхностей их бочек. Известия высших учебных заведений. Черная Металлургия. 2023;66(3):283-289. https://doi.org/10.17073/0368-0797-2023-3-283-289
For citation:
Shalaevskii D.L. Investigation of thermal mode of hot-rolling mill working rolls in order to improve the accuracy of calculating the thermal profile of their barrels’ surface. Izvestiya. Ferrous Metallurgy. 2023;66(3):283-289. https://doi.org/10.17073/0368-0797-2023-3-283-289
Введение
Проблеме исследования теплового профиля бочки рабочего валка непрерывного стана прокатки стальных полос уделяется достаточное внимание в периодической литературе, что говорит об актуальности рассматриваемого вопроса. В работе [1] изложена методика теплового расчета валков широкополосного стана горячей прокатки (ШПСГП), основанная на уравнениях теплового баланса рабочих и опорных валков с учетом их теплообмена друг с другом, полосой, охлаждающей водой и окружающей средой. Точность модели в большей степени будет определяться значениями коэффициентов теплообмена, которые в свою очередь рассчитываются по эмпирическим формулам. В качестве недостатка модели можно отметить невысокую точность учета пауз в ритме прокатки. Учет пауз предлагается осуществлять путем простого умножения доли машинного времени в ритме прокатки на расчетную величину температуры поверхности бочки. При значительных паузах в ритме прокатки расчет по предложенной методике приводит к ошибочным результатам. В качестве достоинства упомянутой модели можно отметить ее относительную простоту использования, достаточную обоснованность и высокий потенциал для совершенствования.
В исследовании [2] рассмотрена упрощенная методика расчета теплового профиля рабочих валков стана горячей прокатки. Методика основана на точном решении уравнения теплопроводности и измерении распределения температуры вдоль бочки рабочих валков после вывалки.
В докладе [3] представлен опыт изменения конструкции коллекторов системы охлаждения с целью снижения температур бочки рабочих валков до допустимого уровня. В указанном докладе, однако, отсутствует теоретическое обоснование выбранного принципа реконструкции и возможность распространения аналогичного принципа на конструкцию систем охлаждения других прокатных станов.
Решение проблемы прогнозирования теплового профиля поверхности бочки рабочего валка является важным, так как этот тепловой профиль может оказать значительное влияние на форму поперечного сечения полосы и качество ее формы [4]. Опыт расчетов показывает, что для этой цели могут быть применены результаты уже упомянутой работы [3], адаптированные для условий рабочих клетей конкретного стана с учетом реальной длительности пауз во время прокатки.
Проблема прогнозирования теплового состояния бочки прокатных валков широкополосных станов поднимается в большом количестве научных трудов.
В работе [5] приведены результаты численного моделирования температурного режима полосы. Исследование проводилось в стационарном режиме. Рабочие валки были представлены в виде двух полых цилиндров, получающих теплоту за счет контакта с заготовкой и охлаждаемых за счет конвекции на ее внешней поверхности и поверхности осевого отверстия. В работе определена зависимость теплового поведения валка от скорости вращения цилиндра и условий теплообмена с окружающей средой.
В публикации [6] представлены результаты исследования нестационарного теплового поля валка в различные моменты времени его работы. Принималось, что теплообмен происходит только по поверхности валка. Полученная по результатам изысканий модель теплового поля позволяет предсказывать температуру в любой точке объема исследуемого валка.
В статье [7] описывается математическая модель, которая в режиме реального времени позволяет рассчитать температуру и тепловое расширение рабочих валков полосовых станов горячей прокатки. Эти результаты используются в экспертной системе, которая управляет подачей охлаждающей воды на бочки рабочих валков.
В исследовании [8] определен коэффициент теплопередачи при горячей прокатке алюминиево-магниевых сплавов на лабораторном стане. Температура раската измерялась с помощью термопар, размещенных внутри материала. Путем обратного расчета по модели получены значения коэффициента в диапазонах от 200 до 450 кВт/(м2ꞏ°C).
В работе [9] авторы разработали конечно-разностную модель для моделирования тепловых расширений рабочих валков CVC при горячей прокатке полосы. При моделировании учитывалось влияние тепловыделения, возникающего в результате деформации и трения полосы, а также конвективного теплообмена с окружающей средой.
Прогнозирование распределения температуры в рабочих валках в процессе горячей прокатки слябов имеет большое значение для проектировщиков стана. В работе [10] проведена оценка зависимости температуры валков и коэффициентов теплообмена в условиях горячей прокатки. С помощью дифференциального уравнения теплопроводности цилиндра получена модель нестационарного теплового режима, позволившая с достаточной точностью оценить температуры рабочих валков.
В работе [11] исследованы дефекты поверхности бочки рабочих валков, вызванные температурными напряжениями. Термические повреждения бочек рабочих валков стана горячей прокатки изучены с использованием лабораторной испытательной установки в условиях, соответствующих условиям первых клетей. Исследования выполнены для валков, изготовленных из двух марок стали: быстрорежущей инструментальной и высокоуглеродистой хромистой. Разработана модель, основанная на методе конечных элементов, для прогнозирования распределения температуры по объему прокатного валка.
В материалах статьи [12] представлен подход на основе метода конечных элементов для анализа термомеханического поведения материала валков при горячей прокатке полосы.
В работе [13] изучено влияние теплового режима прокатных валков на износ поверхности их бочки.
В исследовании [14] предпринята попытка изучения распределения температурного поля в прокатном валке при его взаимодействии с полосой в процессе холодной прокатки. По результатам применения метода конечных элементов предложена методология моделирования неоднородного теплового потока на границе раздела бочка валка – полоса.
В монографии [15] выполнен обзор известных математических моделей теплового режима и охлаждения валков широкополосных станов горячей прокатки. Представлена методика расчета системы охлаждения валков. Описана процедура адаптации расчетных моделей и методик к параметрам действующего стана.
Постановка задачи и методы исследования
Распределение температуры поверхности бочки рабочих валков в большинстве случаев имеет симметричный относительно середины бочки характер. Отмечается [1], что на длине, равной около 2/3 средней ширины полосы, в середине бочки температура почти одинаковая. На участках у кромки полосы температура поверхности бочки несколько снижается, а у торцов бочки эта температура лишь на несколько градусов выше температуры воды, подаваемой на охлаждение. Таким образом, для точного прогнозирования теплового профиля бочки рабочего валка необходимо знать достоверные температуры бочки в ее середине. Определить эти температуры позволяет ряд существующих моделей теплового поля.
Известна балансная модель [16; 17], которая позволяет определить интересующие температуры поверхности бочки рабочих валков в ее середине в клетях «кварто».
Данная модель основана на использовании уравнений теплового баланса бочек рабочего и опорного валков, составленных из допущения, что усредненное температурное поле за отрезок времени, равный ритму прокатки, остается неизменным. Таким образом, все получаемое количество тепловой энергии передается далее контактным теплообменом опорному валку и конвективным теплообменом охлаждающей воде или окружающей среде.
Схема тепловых потоков в радиальной плоскости валков в клети «кварто» представлена на рис. 1. Согласно рис. 1 и описанному принципу теплового обмена валков друг с другом, с охлаждающей водой и окружающей средой, тепловой баланс при описанном квазистационарном режиме может быть представлен двумя уравнениями:
– для рабочего валка:
| \[{Q_{\rm{р}}} - Q_{{\rm{охл.р}}}^{{\rm{вх}}} - Q_{{\rm{охл.р}}}^{{\rm{вых}}} - {Q_{{\rm{оп}}}} = 0;\] | (1) |
– для опорного валка:
| \[{Q_{{\rm{оп}}}} - {Q_{{\rm{ох.оп}}}} - {Q_{{\rm{окр.оп}}}} = 0.\] | (2) |
Рис. 1. Схема тепловых потоков в клети «кварто»: |
В этих уравнениях использованы следующие обозначения количества теплоты: Qр – поступившей в рабочий валок от полосы путем контактного и (частично) лучистого теплообмена; \(Q_{{\rm{охл.р}}}^{{\rm{вх}}}\) и \(Q_{{\rm{охл.р}}}^{{\rm{вых}}}\) – отведенной от рабочего валка охлаждающей водой с входной и выходной сторон рабочей клети; Qоп – переданной от рабочего валка к опорному путем контактного теплообмена; Qохл.оп – отведенной от опорного валка охлаждающей жидкостью; Qокр.оп – отданной опорным валком окружающей среде (воздуху).
После подстановки в представленные уравнения составляющих теплового баланса они могут быть сведены к системе двух линейных уравнений относительно неизвестных средних температур рабочего и опорного валков tср.р.i , tср.оп.i :
\[\left. \begin{array}{r}{A_1}{t_{\rm{р}}} + {B_1}{t_{{\rm{оп}}}} = {D_1};\\{A_2}{t_{\rm{р}}} + {B_2}{t_{{\rm{оп}}}} = {D_2}.\end{array} \right\}\]
Коэффициентами системы обозначены выражения:
\[\left. \begin{array}{r}{A_1} = {\alpha _{{\rm{кт}}{\rm{.р}}}}{l_{{\rm{c}}i}} + \frac{{\pi - {\varphi _4} - {\varphi _1}}}{2}{D_{{\rm{р}}i}}\alpha _{1{\rm{р}}i}^{{\rm{вх}}} + \\ + \frac{{\pi - {\varphi _2}}}{2}{D_{{\rm{р}}i}}\alpha _{1{\rm{р}}i}^{{\rm{вых}}} + {\alpha _{{\rm{кт}}{\rm{.оп}}}}{b_{{\rm{оп}}{\rm{.}}i}};\\{A_2} = {B_1} = - {\alpha _{{\rm{кт}}{\rm{.оп}}}}{b_{{\rm{оп}}{\rm{.}}i}};\\{B_2} = \frac{{{\varphi _5}}}{2}{D_{{\rm{оп}}{\rm{.}}i}}{\alpha _{1{\rm{оп}}}} + {\alpha _{{\rm{кт}}{\rm{.оп}}}}{b_{{\rm{оп}}{\rm{.}}i}} + (2\pi - {\varphi _5})\frac{{{D_{{\rm{оп}}{\rm{.}}i}}}}{2}{\alpha _{{\rm{окр}}{\rm{.оп}}}};\\{D_1} = {\alpha _{{\rm{кт}}{\rm{.р}}}}{l_{{\rm{c}}i}}{t_{\rm{п}}} + \frac{{\pi - {\varphi _4} - {\varphi _1}}}{2}{D_{{\rm{р}}i}}\alpha _{1{\rm{р}}i}^{{\rm{вх}}}{t_{{\rm{охл}}.1}} + \\ + \frac{{\pi - {\varphi _2}}}{2}{D_{{\rm{р}}i}}\alpha _{1{\rm{р}}i}^{{\rm{вых}}}{t_{{\rm{охл}}.1}};\\{D_2} = \frac{{{\varphi _5}}}{2}{D_{{\rm{оп}}{\rm{.}}i}}{\alpha _{1{\rm{оп}}}}{t_{{\rm{охл}}.1}} + (2\pi - {\varphi _5})\frac{{{D_{{\rm{оп}}{\rm{.}}i}}}}{2}{\alpha _{{\rm{окр}}{\rm{.оп}}}}{t_{{\rm{окр}}}}.\end{array} \right\}\]
В этих формулах приняты следующие обозначения входящих величин:
– коэффициенты теплоотдачи контактным теплообменом: αкт.р – от полосы к рабочему валку; αкт.оп – от рабочего валка к опорному;
– коэффициенты теплоотдачи конвективным теплообменом: \(\alpha _{1{\rm{р}}i}^{{\rm{вх}}}\), \(\alpha _{1{\rm{р}}i}^{{\rm{вых}}}\) – от рабочих валков к охлаждающей воде на входной и выходной сторонах рабочей клети; α1оп – от опорных валков к охлаждающей воде; αокр.оп – от опорных валков к воздуху (размерность всех коэффициентов теплоотдачи Вт/(м2ꞏ°C));
– углы по окружностям бочек рабочего и опорных валков, ограничивающих зоны с разными коэффициентами теплоотдачи: φ1 – φ5 в радианах (рис. 1);
– остальные величины: Dрi , Dопi – диаметры в середине бочки рабочего и опорного валков i-й клети, м; lci – длина очага деформации i-й клети, м (вычисляется заранее в модели усилия прокатки, изложенной выше); bопi – ширина площадки упругого контакта между рабочим и опорным валками, м (вычисляется по формуле Герца из теории упругости); tохл – температура охлаждающей воды, подаваемой на валки, °С; tвыхi – температура полосы на выходе из очага деформации i-й клети (рассчитывается заранее по формулам частной модели температуры полосы, изложенной выше); tокр – температура окружающей среды (воздуха), °С.
Решение системы уравнений теплового баланса рабочего и опорного валков может быть найдено методом Крамера в виде:
| \[\left. \begin{array}{r}{t_{\rm{р}}} = \frac{{{B_2}{D_1} - {B_1}{D_2}}}{{{A_1}{B_2} - {A_2}{B_1}}};\\{t_{{\rm{оп}}}} = \frac{{{A_1}{D_2} - {A_2}{D_1}}}{{{A_1}{B_2} - {A_2}{B_1}}}.\end{array} \right\}\] | (3) |
Наиболее важными параметрами, влияющими на достоверность расчета температур валков, являются теплофизические постоянные – коэффициенты контактного и конвективного теплообменов: αкт.р , αкт.оп , \(\alpha _{1{\rm{р}}i}^{{\rm{вх}}}\), \(\alpha _{1{\rm{р}}i}^{{\rm{вых}}}\), α1оп , αокр.оп .
Расчетные формулы для определения коэффициентов конвективного теплообмена и конкретные значения этих коэффициентов \(\alpha _{1{\rm{р}}i}^{{\rm{вх}}}\), \(\alpha _{1{\rm{р}}i}^{{\rm{вых}}}\), α1оп , αокр.оп представлены в работах [16; 17]. Так, коэффициенты конвективного теплообмена опорного валка и охлаждающей воды, опорного валка и окружающей среды по данным этих работ составят соответственно: α1оп = 1500 Вт/(м2ꞏ°С); αокр.оп = 400 Вт/(м2ꞏ°С), а коэффициент контактного теплообмена опорного валка и рабочего αкт.оп = 40 кВт/(м2ꞏ°С).
Коэффициент конвективного теплообмена рабочего валка и охлаждающей воды может быть определен по формуле [17]
| α1р.вх ≈ α1р.вых = 21V11 + 21 000pохл – 0,04\(V_{11}^2\) – 71\(p_{{\rm{охл}}}^2\) – 14 590, Вт/(м2·°С), | (4) |
где V11 – плотность облива поверхности бочки по ширине полосы \(\left( {{V_{11}} = \frac{V}{{{\varphi _3}R{b_{\rm{п}}}}}} \right)\), м3/(с·м2), V – суммарный расход воды, подаваемой на рабочие валки i-й клети, м3/с; bп – ширина полосы, м); pохл – давление воды в системе охлаждения при подаче на поверхность рабочих валков, атм.
Коэффициент контактного теплообмена валка и полосы αкт.р , очевидно, будет зависеть от:
– длины очага деформации, определяемой опосредовано контактными напряжениями;
– продолжительности контакта полосы и бочки валка в ритме прокатки, которая может быть выражена коэффициентом ритма прокатки: \({K_{{\rm{ритма}}}} = \frac{{{\tau _{\rm{м}}}}}{{{\tau _{\rm{м}}} + {\tau _{\rm{п}}}}}\) (τм – машинное время работы стана, с; τп – время пауз, когда в очаге деформации нет полосы, с);
– диаметра бочки валка (диаметр бочки валка в условиях конкретного стана и клети будет неизменным);
– наличия окалины между материалом полосы и поверхностью валка.
Стоит отметить, что достоверное определение коэффициента контактного теплообмена αкт.р в значительной степени определит точность расчета температуры рабочего валка и зависящих от него параметров теплового режима.
Выражение для αкт.р может быть найдено на основании опытных данных, содержащих значения технологических и энергосиловых параметров процесса прокатки и конструктивных параметров клети, а также результаты опытного определения температур поверхности бочки валка.
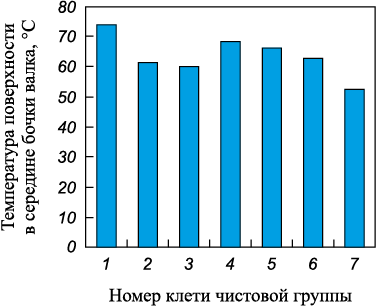
Подобные исходные данные для определения коэффициента αкт.р для условий непрерывной чистовой группы клетей широкополосного стана горячей и холодной прокатки были определены из ряда источников [16 – 18]. Температуры поверхностей бочек рабочих валков, указанные в литературных источниках, измерялись с помощью термопары сразу после извлечения рабочих валков из клети. Гистограммы распределения температур в середине длины бочек рабочих валков по клетям чистовой группы широкополосного стана 2000 представлены на рис. 2.
Рис. 2. Температуры поверхностей бочек рабочих валков |
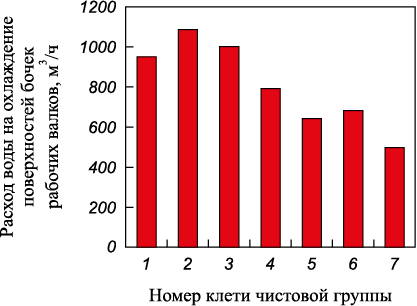
Из приведенных данных можно увидеть тенденцию по снижению температур бочек рабочих валков от первой клети чистовой группы к последней, что может быть объяснено уменьшением температуры полосы в этих клетях. Исключение представляют вторая и третья клети, в которых, как следует из рис. 3, средние значения расходов воды, подаваемой на поверхности бочек валков, являются наибольшими в сравнении с расходами воды в других клетях.
Рис. 3. Расходы воды на охлаждение поверхностей бочек |
Для определения уравнения, с помощью которого может быть найден коэффициент контактного теплообмена поверхности рабочего валка и поверхности полосы, были подобраны значения упомянутых коэффициентов, использование которых в балансной модели теплового режима обеспечит минимальное расхождение измеренных и расчетных температур. Далее методом регрессионного анализа определено наилучшее уравнение, которое обеспечит расчет коэффициента αкт.р , проведена оценка значимости влияющих факторов и адекватности найденного выражения.
Результаты исследования и их обсуждение
Методами регрессионного анализа экспериментальных данных получено уравнение, позволяющее определять коэффициент контактного теплообмена рабочих валков и стальной полосы в очагах деформации рабочих клетей чистовой группы ШПСГП. Уравнение имеет следующий вид:
αкт.р = 6,6 pсрi + 103(70,7Kритма – 48,2\(K_{{\rm{ритма}}}^2\) – 22,75), Вт/(м2·°С),
где pсрi – среднее контактное давление в очаге деформации; Kритма – коэффициент ритма прокатки.
Диапазоны изменения значений параметров, по которым определялось выражение для расчета αкт.р , составляли: Kритма = 0,46 – 0,90 б/р; pсрi = 200 – 600 МПа.
В представленное уравнение включены только значимые факторы, установленные критерием Стьюдента t и уровнем значимости α.
Адекватность модели коэффициента теплообмена проверена с помощью критерия Фишера. Проверка достоверности балансной модели валков с использованием найденного уравнения для коэффициента уравнений αкт.р на статистически значимом массиве данных показала, что средняя погрешность расчета величин tср.рi (расхождения между измеренными и рассчитанными значениями) составила 8,01 %, максимальная – 16,7 %, минимальная – 1,53 %, показатель R2 = 0,87.
Таким образом, найденное выражение для коэффициента контактного теплообмена, благодаря достоверности, позволяет использовать балансную модель для поиска теплового профиля валков рабочих клетей НШПСГП в расчетах (например, поперечного профиля или плоскостности готовой полосы или наилучшей формы исходной профилировки поверхности бочки рабочего валка) [19]. Также такой подход может быть использован для оценки поперечного профиля холоднокатаных полос [20].
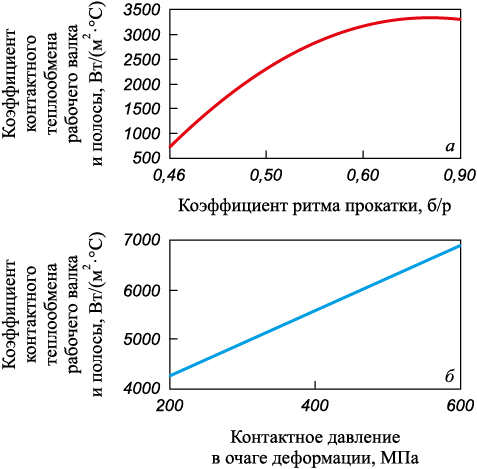
Опытные данные в сочетании с найденной зависимостью позволили оценить уровень влияния ритма прокатки и контактного давления на интенсивность теплообмена рабочего валка и полосы (рис. 4). Коэффициент ритма прокатки и контактное давление, изменяющиеся в допустимых технологией диапазонах, способны существенно изменить коэффициент контактного теплообмена и, следовательно, поменять тепловой профиль валка. Наиболее значимое влияние на теплообмен полосы и поверхности бочки рабочего валка оказывает ритм прокатки. Это влияние особенно сильно проявляется при коэффициенте ритма прокатки менее 0,6.
Рис. 4. Влияние факторов прокатки на коэффициент контактного теплообмена |
Выводы
Тепловой режим бочки рабочего валка стана горячей прокатки – значимый фактор технологии, который влияет на качество формы стальной полосы, ее поперечное сечение и стойкость рабочих валков. Достоверный расчет параметров температурного режима позволит определить форму теплового профиля и наилучшую профилировку поверхности бочки валка, добиться уменьшения дефектов планшетности готового проката. Наиболее распространенной является балансная модель теплового режима валка, точность которой в значительной степени определяется теплофизическими постоянными, в частности коэффициентами теплообмена валков: контактного – с полосой и конвективного – с охлаждающей водой. В литературе встречаются различные сведения о значениях и методах расчета этих коэффициентов, но большинство из них не учитывают наличие пауз в ритме прокатки чистовой группы клетей, которые имеют большую продолжительность. Отсутствие учета этого фактора влечет за собой значительные ошибки в расчетах теплового режима бочки валка.
Проведен пассивный эксперимент, в ходе которого с помощью термопары измерены температуры поверхности бочки рабочих валков в нескольких точках по их длине сразу же после вывалки. Также определены параметры прокатки стальных полос перед перевалкой: коэффициенты ритма прокатки, обжатия полосы в клетях, расходы воды на охлаждение валков и некоторые другие параметры. В результате получено эмпирическое уравнение для расчета коэффициента контактного теплообмена, учитывающее основные факторы технологии, в том числе длительность пауз в ритме прокатки. Использование уточненных выражений для поиска теплофизических коэффициентов, необходимых для расчета температур бочки валка, значительно повысит точность прогнозирования теплового режима.
Установлено, что коэффициент ритма прокатки и контактное давление, изменяющиеся в допустимых технологией диапазонах, способны существенно изменить коэффициент контактного теплообмена и, следовательно, поменять тепловой профиль бочки. Причем наиболее значимое влияние на теплообмен полосы и поверхности бочки рабочего валка оказывает ритм прокатки. Это влияние особенно сильно проявляется при коэффициенте ритма прокатки менее 0,6.
Список литературы
1. Гарбер Э.А., Хлопотин М.В., Трайно А.И., Попов Е.С., Савиных А.Ф. Моделирование теплового режима валков широкополосного стана горячей прокатки для определения эффективных режимов их охлаждения. Металлы. 2009;(3):34–47.
2. Бельский С.М., Мазур И.П., Астахов А.А. Упрощенная методика вычисления тепловой профилировки рабочих валков стана горячей прокатки. Производство проката. 2018;(2):3–6.
3. Антонюк В.В., Федин А.Г., Мустафин В.А., Дема Р.Р., Платов С.И., Амиров Р.Н., Колдин А.В. Харченко М.В. Опыт настройки и управления тепловым состоянием рабочих валков широкополосного стана 2000 горячей прокатки ПАО «Магнитогорский металлургический комбинат». Материалы ХI Международного конгресса прокатчиков. Том 2. 2017.
4. Гарбер Э.А., Мишнев П.А., Шалаевский Д.Л., Палигин Р.Б., Михеева И.А., Болобанова Н.Л. Новые методы моделирования и уменьшения неплоскостности стальных полос при горячей прокатке на широкополосных станах. Материалы Международного научного семинара «Научно-технический прогресс в металлургии – 2013». 2014:70–82.
5. Hamraoui M. Thermal behaviour of rollers during the rolling process. Applied Thermal Engineering. 2009;29(11–12): 2386–2390. https://doi.org/10.1016/j.applthermaleng.2008.12.013
6. Johnson R.E., Keanini R.G. An asymptotic model of work roll heat transfer in strip rolling. International Journal of Heat and Mass Transfer. 1995;41(6–7):871–879. https://doi.org/10.1016/S0017-9310(97)00175-0
7. Campos A.M., Garcia D.F., Usamentiaga R., de Abajo N., Gonzalez J.A. Real time model for the intelligent control of cooling systems for hot strip mill work rolls. 26th Annual Conference of the IEEE. 2000. https://doi.org/10.1109/IECON.2000.972272
8. Hlady C.O., Brimacombe J.K., Samarasekera I.V., Hawbolt E.B. Heat transfer in the hot rolling of the metal. Metallurgical and Material Transactions B. 1995;26:1019–1027. https://doi.org/10.1007/BF02654104
9. Zhang X.M., Yiang Z.Y., Tieau A.K., Liu X.N., Wang G.D. Numerical modeling of the thermal deformation of CVC work rolls in hot strip rolling. Journal of Material Processing Technology. 2002;130–131:219–223. https://doi.org/10.1016/S0924-0136(02)00736-7
10. Serajzadeh S., Karemi Taheri A., Mucciardi F. Unsteady state work-roll temperature distribution during continuous hot slab rolling. International Journal of Mechanical Sciences. 2002;44(12):2447–2462. https://doi.org/10.1016/S0020-7403(02)00179-0
11. Mercado-Solis R.D., Talamantes-Silva J., Beynon J.H., Hernandes-Rodrigues M.A.L. Modelling surface thermal damage to mill rolls. Wear. 2007;263(17–20):1560–1567. https://doi.org/10.1016/j.wear.2006.12.062
12. Hwang S.M., Sun C.G., Ryoo S.R., Kwak W.J. An itegrated FE process model for prevision analysis of the thermo-mechanical behaviours of rolls and strip in hot strip rolling. Computer Methods in Applied Mechanics and Engeneering. 2002;191:4015–4033. https://doi.org/10.1016/S0045-7825(02)00298-0
13. Kotrbacek P., Horsky J., Raudensky M., Pohanka M. Experimental study of heat transfer in hot rolling. Revue de Métallurgie. 2006;103(7–8):333–341. https://doi.org/10.1051/metal:2006134
14. Arif A.F., Khan O., Zubair S.M. Prediction of roll temperature with a non-uniform heat flux at tool and workpiece interface. Heat and Mass Transfer. 2004;41(1):75–94. https://doi.org/10.1007/s00231-004-0508-6
15. Гарбер Э.А. Моделирование и совершенствование теплового режима и профилировок валков: Монография. Череповец: ЧГУ; Москва: Теплотехник; 2013:114.
16. Гарбер Э.А., Хлопотин М.В., Савиных А.Ф., Кожевников А.В., Голованов А.В., Смирнов В.С. Промышленные испытания усовершенствованных профилировок рабочих валков на широкополосном стане горячей прокатки. Производство проката. 2008;(4):18–22.
17. Гарбер Э.А., Хлопотин М.В., Попов Е.С., Савиных А.Ф., Голованов А.В. Повышение эффективности охлаждения валков широкополосного стана горячей прокатки с использованием адаптивных математических моделей теплового баланса. Производство проката. 2009;(4):12–24.
18. Гарбер Э.А. Станы холодной прокатки. Москва: Черметинформация; 2004.
19. Гарбер Э.А., Мишнев П.А., Шалаевский Д.Л., Палигин Р.Б., Михеева И.А., Болобанова Н.Л. Моделирование и уменьшение неплоскостности полос при горячей прокатке на стадии настройки широкополосного стана. Производство проката. 2014;(3):7–13.
20. Шалаевский Д.Л., Корепина К.П. Исследование влияния поперечного профиля холоднокатаных полос на возникновение дефектов планшетности. Черные металлы. 2022;(3):56–59.
Об авторе
Д. Л. ШалаевскийРоссия
Дмитрий Леонидович Шалаевский, к.т.н., доцент кафедры металлургии, машиностроения и технологического оборудования
Россия, 162600, Вологодская обл., Череповец, пр. Луначарского, 5
Рецензия
Для цитирования:
Шалаевский Д.Л. Исследование теплового режима рабочих валков стана горячей прокатки с целью повышения точности расчета температур поверхностей их бочек. Известия высших учебных заведений. Черная Металлургия. 2023;66(3):283-289. https://doi.org/10.17073/0368-0797-2023-3-283-289
For citation:
Shalaevskii D.L. Investigation of thermal mode of hot-rolling mill working rolls in order to improve the accuracy of calculating the thermal profile of their barrels’ surface. Izvestiya. Ferrous Metallurgy. 2023;66(3):283-289. https://doi.org/10.17073/0368-0797-2023-3-283-289