Scroll to:
Investigation of thermal mode of hot-rolling mill working rolls in order to improve the accuracy of calculating the thermal profile of their barrels’ surface
https://doi.org/10.17073/0368-0797-2023-3-283-289
Abstract
Thermal mode of the working roll barrel in a hot-rolling mill is a significant technological factor that affects the steel strip quality, its cross section, and durability of working rolls. A reliable calculation of the temperature mode parameters makes it possible to determine the thermal profile shape and the best profiling of the roll barrel surface, as well as to reduce defects in steel strip flatness. The most common is the balance model of roll thermal mode. Its accuracy is largely determined by thermophysical constants, in particular, the heat transfer coefficients of the rolls: contact – with the strip and convective – with cooling water. There are various data on the values and methods for calculating these coefficients, but most of them do not take into account the presence of pauses in rolling rhythm of the finishing group of stands, the duration of which is significant. Failure to take this factor into account entails significant errors in calculations of the thermal mode. A passive experiment was carried out, during which surface temperatures of the working rolls’ barrels were measured using a thermocouple at several points along their length immediately after they fell out. Also, the parameters of steel strip rolling before roll change were determined: rolling rhythm coefficients, strip reduction in stands, water consumption for cooling rolls and some others. As a result, an empirical equation was obtained for calculating the contact heat transfer coefficient, taking into account the main technological factors. The use of refined coefficients for calculating the temperatures of the roll barrel significantly increased the accuracy of predicting the thermal mode, in particular, the thermal profile of the working roll, based on values of the rolling parameters.
Keywords
For citations:
Shalaevskii D.L. Investigation of thermal mode of hot-rolling mill working rolls in order to improve the accuracy of calculating the thermal profile of their barrels’ surface. Izvestiya. Ferrous Metallurgy. 2023;66(3):283-289. https://doi.org/10.17073/0368-0797-2023-3-283-289
Introduction
Numerous studies have been conducted on the temperature profiles of roll body in continuous rolling mills. Garber E. et al. [1] proposed a thermal analysis approach for broad-strip hot rolling mill rolls. Their method incorporated heat balance equations for work rolls (WR) and backup rolls (BR) considering heat exchange between the rolls, strip, cooling water, and the environment. The accuracy of their simulation heavily relied on empirically estimated heat transfer coefficients. However, a disadvantage of their model was the insufficient consideration of rolling downtime. To address this, the fraction of operating time during the lead time was multiplied by the roll body temperature, leading to significant errors during extended downtime. Despite this limitation, the simulation model was relatively simple, valid to a certain extent, and had potential for improvement.
Bel’skii S. et al. [2] employed a simplified model to estimate the temperature profile of hot-rolling work rolls. They obtained an exact solution for the thermal conductivity equation and measured the temperature distribution along the roll body after rolling.
Antonyuk V. et al. [3] introduced a new design for cooling system headers aimed at reducing the work roll body temperature to an acceptable level. However, their study lacked any theoretical analysis of the proposed upgrade, and it remained unclear whether the design could be applied to cooling systems of other rolling mills.
Garber E. et al. [4] demonstrated the significant impact the roll body temperature profile on the accuracy of strip cross-section shape [4]. The model presented in [3] could be applied with adjustments specific to the rolling mill and actual downtime.
Several studies have focused on temperature profiles in broad-strip rolling mill.
Hamraoui M. et al. [5] simulated the strip temperature distribution in the steady-state mode, representing work rolls as heated hollow cylinders in contact with the strip and cooled by convection on the outer and axial hole surface. They proposed a model linking roll temperature to its rotation speed and heat exchange with the environment.
Johnson R. et al. [6] investigated the unsteady thermal field of the roll at different time intervals, assuming heat transfer solely on the roll surface. Their resulting thermal field model enabled temperature prediction at any point within the roll body.
Campos A. et al. [7] developed a real-time simulation model to estimate the temperature and thermal expansion of hot-rolling mill work rolls. Additionally, they designed an intelligent system to control the cooling water flow rate for work rolls.
Hlady C. et al. [8] determined the heat transfer coefficient for hot rolling of aluminum-magnesium alloys in a laboratory mill. They placed thermocouples inside the rolling strip and obtained coefficient values ranging from 200 to 450 kW/(m2·°C) through inverse modeling.
Zhang X. et al. [9] created a finite-difference model to simulate the thermal expansions of CVC work rolls during hot strip rolling. Their simulation considered heat release resulting from strip deformation and friction, as well as convective heat exchange with the environment.
Prediction of temperature distribution in work rolls holds great importance for mill designers. Serajzadeh S. et al. [10] estimated the temperature and heat transfer coefficients of hot-rolling roll. By utilizing the differential equation of thermal conductivity for cylinders, they derived a nonstationary thermal model which provided reasonably accurate estimates of work roll temperature.
Mercado-Solis R. et al. [11] examined surface defects in work roll bodies caused by temperature stress. They studied heat damage to hot-rolling mill work rolls using a test bench that simulated the first stands. Two steel grades were tested: high-speed tool steel and high-carbon chromium steel. Their FEM model predicted temperature distribution across the roll volume.
Hwang S. et al. [12] presented a FEM approach to analyze the thermal and mechanical behavior of hot strip rolls.
Kotrbacek P. et al. [13] conducted a study on the impact of roll temperature on roll body wear.
Arif A. et al. [14] examined the temperature distribution in the work roll when it comes into contact with the strip during cold rolling. They proposed a FEM approach to simulate the inhomogeneous heat flow at the interface between the roll body and strip.
In his monograph, Garber E. [15] provided a comprehensive review of existing simulation models for cooling broad-strip rolling mill rolls. The monograph also includes an analysis of the roll cooling system and discusses the adaptation of simulation models to specific rolling mill.
Problem statement. Materials and methods
In most cases, the temperature distribution across the surface of WR body is symmetric relative to the roll body’s midline. This symmetry is maintained up to approximately two-thirds of the average strip width [1]. The roll surface temperature experiences a slight decrease towards the strip edges, while the roll ends are only a few degrees hotter than the cooling water. To predict the temperature profile, it is necessary to determine the actual temperature at the middle of the roll body. This temperature can be obtained using available temperature distribution models.
The heat balance model [16; 17] utilized to calculate the temperature at the middle of the roll body surface in 4-high mill stands.
This model employs thermal balance equations for the WR and BR, assuming that the average temperature field over the rolling lead time remains constant. According to this model, the entire heat energy generated is transferred through contact heat exchange to the backup roll and through convective heat exchange to either the cooling water or the environment.
Fig. 1 illustrates the heat flows in the radial plane of the rolls for a 4-high mill stand. Based on Fig. 1 and the aforementioned patterns of roll-to-roll, roll-to-cooling water, and roll-to-environment heat exchange, the quasi-stationary heat balance can be represented by the following two equations:
– for the work roll:
| \[{Q_{\rm{wr}}} - Q_{{\rm{wr.cool}}}^{{\rm{in}}} - Q_{{\rm{wr.cool}}}^{{\rm{out}}} - {Q_{{\rm{br}}}} = 0;\] | (1) |
– for the backup roll:
| \[{Q_{{\rm{br}}}} - {Q_{{\rm{br.cool}}}} - {Q_{{\rm{br.env}}}} = 0.\] | (2) |
Fig. 1. Scheme of heat flows in the “quarto” stand: |
In these equations, the heat amounts are defined as follows: Qwr represents the heat supplied to the WR from the strip through contact and partially radiant heat exchange; \(Q_{{\rm{wr.cool}}}^{{\rm{in}}}\) and \(Q_{{\rm{wr.cool}}}^{{\rm{out}}}\) denote the amounts of heat removed from the WR by the cooling water at the inlet and outlet of the stand; Qbr represents the heat transferred from the WR to BR through contact heat exchange; Qbr.cool represents the heat removed by the cooling water from the backup roll; Qbr.env represents the heat released by the backup roll to the environment (air).
By substituting the heat balance components in the equations above they are reduced to a system of two linear equations in the unknown average temperatures of the WR (tavg.wr.i ) and BR (tavg.br.i ):
\[\left. \begin{array}{r}{A_1}{t_{\rm{wr}}} + {B_1}{t_{{\rm{br}}}} = {D_1};\\{A_2}{t_{\rm{wr}}} + {B_2}{t_{{\rm{br}}}} = {D_2}.\end{array} \right\}\]
The coefficients of the system of equations are expressed as follows:
\[\left. \begin{array}{r}{A_1} = {\alpha _{{\rm{cont.hr}}{\rm{.wr}}}}{l_{{\rm{s}}i}} + \frac{{\pi - {\varphi _4} - {\varphi _1}}}{2}{D_{{\rm{wr}}i}}\alpha _{1{\rm{wr}}i}^{{\rm{in}}} + \\ + \frac{{\pi - {\varphi _2}}}{2}{D_{{\rm{wr}}i}}\alpha _{1{\rm{wr}}i}^{{\rm{out}}} + {\alpha _{{\rm{cont.hr}}{\rm{.br}}}}{b_{{\rm{br}}{\rm{.}}i}};\\{A_2} = {B_1} = - {\alpha _{{\rm{cont.hr}}{\rm{.br}}}}{b_{{\rm{br}}{\rm{.}}i}};\\{B_2} = \frac{{{\varphi _5}}}{2}{D_{{\rm{br}}{\rm{.}}i}}{\alpha _{1{\rm{br}}}} + {\alpha _{{\rm{cont.hr}}{\rm{.br}}}}{b_{{\rm{br}}{\rm{.}}i}} + (2\pi - {\varphi _5})\frac{{{D_{{\rm{br}}{\rm{.}}i}}}}{2}{\alpha _{{\rm{br}}{\rm{.env}}}};\\{D_1} = {\alpha _{{\rm{cont.hr}}{\rm{.wr}}}}{l_{{\rm{s}}i}}{t_{\rm{s}}} + \frac{{\pi - {\varphi _4} - {\varphi _1}}}{2}{D_{{\rm{wr}}i}}\alpha _{1{\rm{wr}}i}^{{\rm{in}}}{t_{{\rm{cool}}.1}} + \\ + \frac{{\pi - {\varphi _2}}}{2}{D_{{\rm{wr}}i}}\alpha _{1{\rm{wr}}i}^{{\rm{out}}}{t_{{\rm{cool}}.1}};\\{D_2} = \frac{{{\varphi _5}}}{2}{D_{{\rm{оп}}{\rm{.}}i}}{\alpha _{1{\rm{оп}}}}{t_{{\rm{cool}}.1}} + (2\pi - {\varphi _5})\frac{{{D_{{\rm{br}}{\rm{.}}i}}}}{2}{\alpha _{{\rm{br}}{\rm{.env}}}}{t_{{\rm{env}}}}.\end{array} \right\}\]
The input values for the system of equations are as follows:
– contact heat transfer coefficients: αcont.ht.wr strip to WR; αcont.ht.br WR to BR;
– convective heat transfer coefficients: \(\alpha _{1{\rm{wr}}i}^{{\rm{in}}}\), \(\alpha _{1{\rm{wr}}i}^{{\rm{out}}}\) WR to cooling water at the stand inlet and outlet; α1br BR to the cooling water; αbr.env BR to the air (all the heat transfer coefficients are in W/(m2ꞏ°C));
– φ1 to φ5 are the WR and BR circumference angles in radians which define sectors with different heat transfer coefficients (refer Fig. 1);
– other values: Dwri , Dbri mid-body diameters of the i\(^{\rm{th}}\) stand WR and BR, m; lsi length deformation area for the i\(^{\rm{th}}\) stand, m (pre-estimated using the rolling force model); bbri width of the elastic contact area between the WR and BR, m (estimated using the Hertzian equations from elasticity theory); tcool temperature of the cooling water supplied to the rolls, °C; touti strip temperature as it leaves the deformation area of the i\(^{\rm{th}}\) stand (pre-estimated with the partial strip temperature model); tenv ambient (air) temperature, °C.
The WR and BR heat balance equations were solved using Cramer’s rule:
| \[\left. \begin{array}{r}{t_{\rm{wr}}} = \frac{{{B_2}{D_1} - {B_1}{D_2}}}{{{A_1}{B_2} - {A_2}{B_1}}};\\{t_{{\rm{br}}}} = \frac{{{A_1}{D_2} - {A_2}{D_1}}}{{{A_1}{B_2} - {A_2}{B_1}}}.\end{array} \right\}\] | (3) |
The reliability of roll temperature estimation depends on the contact and convective heat transfer coefficients: αcont.ht.wr , αcont.ht.br , \(\alpha _{1{\rm{wr}}i}^{{\rm{in}}}\), \(\alpha _{1{\rm{wr}}i}^{{\rm{out}}}\), α1br , αbr.env .
Garber E. et al. [16; 17] presented equations for the \(\alpha _{1{\rm{wr}}i}^{{\rm{in}}}\), \(\alpha _{1{\rm{wr}}i}^{{\rm{out}}}\), α1br , αbr.env coefficients. The convective heat transfer coefficients between BR and cooling water, and BR and environment (air) in these papers are: α1br = 1500 W/(m2ꞏ°С); αbr.env = 400 W/(m2ꞏ°С), the contact heat transfer coefficient between WR and BR αcont.ht.br = 40 kW/(m2ꞏ°С).
The equation for the convective heat transfer coefficient between WR and cooling water is given by [17]
| α1wr.in ≈ α1wr.out = 21V11 + 21,000pcool – 0.04\(V_{11}^2\) – 71\(p_{{\rm{cool}}}^2\) – 14,590, W/(m2·°С), | (4) |
where V11 is the water spraying intensity over the roll body width \(\left( {{V_{11}} = \frac{V}{{{\varphi _3}R{b_{\rm{s}}}}}} \right)\), m3/(s·m2), V is the total volume of water supplied to the WRs of the i\(^{\rm{th}}\) stand, m3/s; bs is the strip width, m); pcool is the WR cooling water pressure, atm.
The roll-to-strip contact heat transfer coefficient αcont.ht.wr depends on:
– the length of the deformation area, which in turn is determined by the contact stress;
– the roll body-to-strip contact period expressed as the downtime ratio: \({K_{{\rm{dr}}}} = \frac{{{\tau _{\rm{lt}}}}}{{{\tau _{\rm{lt}}} + {\tau _{\rm{dr}}}}}\) (τlt is the lead time, s; τdr is the downtime when there is no strip in the deformation area, s);
– the roll body diameter (assumed constant for the specific rolling mill and stand);
– the presence of slag between the strip and the roll surface.
It is important to emphasize that the accuracy of the αcont.ht.wr contact heat transfer coefficient will greatly influence the accuracy of work roll temperature estimation and other temperature-dependent process properties.
The determination of αcont.ht.wr can be achieved by utilizing experimental data of process variables, stand properties, and experimental studies of roll body surface temperature.
Papers [16 – 18] provide such input data for calculating the αcont.ht.wr coefficient in the finishing stands of a broad-strip cold and hot rolling mill. The literature reports temperatures of work roll body surfaces that are measured using thermocouples immediately after the work rolls are removed from the stand. Fig. 2 illustrates bar graphs depicting the temperature distribution in the middle of the WR body for the finishing stand of the 2000 model broad-strip rolling mill.
Fig. 2. Temperatures of the working rolls barrels’ surfaces |
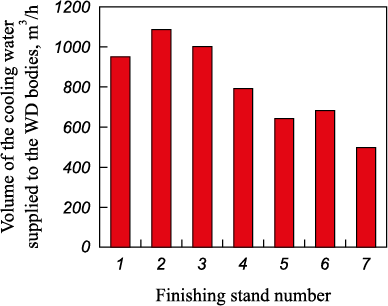
Fig. 2 indicates that the roll body temperature generally decreases from the first stand to the last finishing stand. This can be attributed to the lower strip temperature in these stands. However, the second and third stands deviate from this trend. Fig. 3 demonstrates that the average flow rates of water supplied to the roll body surfaces are highest compared to the flow rates in the other stands.
Fig. 3. Water consumption for cooling the working rolls barrels’ |
To derive an analytic equation for the WR-to-strip contact heat exchange coefficient we determined the coefficient values that minimize the discrepancy between measured and estimated temperatures using the heat balance model. Subsequently, they selected the most suitable equation for αcont.ht.wr and validated its performance.
Results and discussion
We conducted regression analysis on the experimental data to develop an equation for the WR-to-strip contact heat exchange coefficient in the deformation areas of the finishing stands in the broad-strip rolling mill. The resulting equation is as follows:
αcont.ht.wr = 6.6 pavgi + 103(70.7Kdr – 48.2\(K_{{\rm{dr}}}^2\) – 22.75), W/(m2·°С),
where pavgi represents the average contact pressure at the center of deformation; Kdr denotes the downtime ratio.
The ranges of the values used to establish the expression for αcont.ht.wr are as follows: Kdr = 0.46 – 0.90; pavgi = 200 – 600 MPa.
The equation includes significant factors which were determined based on the results of Student’s t-test with an α significance level.
To validate the equation for the heat transfer coefficient, Fisher’s criterion was employed. Both the heat balance model and the αcont.ht.wr equation were validated using a statistically significant dataset. The average tavg.wri (discrepancy between the estimated and measured value) was 8.01 %. The maximum discrepancy was 16.7 %, the minimum was 1.53 %, and R2 = 0.87.
Consequently, the expression for the contact heat transfer coefficient can be considered reliable. The heat balance model can be utilized to estimate the roll temperature profile and other properties, such as the dimensions of the strip cross-section or the optimal shape of the WR body, in broad-strip rolling mills [19]. This approach can also be applied to estimate the cross-section shape of cold-rolled strips [20].
Based on the experimental data and the equation for the WR-to-strip contact heat exchange coefficient, we conducted an analysis to estimate the impact of the downtime ratio and contact pressure on the heat exchange intensity between the WR and strip (Fig. 4). The results depicted in Fig. 4 indicate that the downtime ratio and contact pressure, when within the acceptable ranges, can exert a significant influence on the contact heat transfer coefficient and, consequently, the heat profile of the roll. Specifically, the downtime ratio demonstrates the most substantial effect on the WR-to-strip heat exchange, particularly when the downtime ratio falls below 0.6.
Fig. 4. Influence of rolling factors on the coefficient of contact heat transfer |
Conclusions
The roll body temperature plays a crucial role in hot rolling processes as it impacts various aspects such as the shape and dimensions of the rolled steel and the lifespan of the roll itself. To achieve an accurate estimation of the roll temperature and obtain its temperature profile, it is essential to employ a reliable heat balance model. This model enables the determination of the optimal shape of the roll body and aids in minimizing flatness defects. The accuracy of the heat balance model heavily relies on the constants associated with heat transfer coefficients. In the context of roll temperature estimation, there are two types of heat transfer that are of particular importance: contact heat transfer between the roll and the strip, and convective heat transfer between the roll and the cooling water. The available literature sources provide diverse values and equations for the contact and convective heat transfer coefficients in roll temperature analysis. However, many of these sources overlook the impact of long breaks during the operation of the finishing stand. As a result, significant errors can arise in the analysis of roll temperature.
To address this issue, we conducted measurements of the actual roll body temperature at multiple points along the roll length using thermocouple immediately after rolling. Additionally, we collected data on various rolling process variables, such as downtime ratio, reduction ratio for each stand, cooling water flow rate, and others, prior to the transfer of the steel strip. Based on these measurements and process variable values, we derived an empirical equation for the contact heat transfer coefficient that incorporates the key process variables, including the downtime ratio. By utilizing these refined coefficients, we significantly improved the accuracy of the roll temperature profile obtained from the process variable values.
Our findings indicate that the downtime ratio and contact pressure, when within acceptable ranges, exert a substantial influence on the contact heat transfer coefficient and, consequently, the heat profile of the roll body. Particularly, the downtime ratio exhibits the most significant impact on the heat exchange between the work roll and the strip, especially when the downtime ratio is below 0.6.
References
1. Garber E.A., Khlopotin M.V., Traino A.I., Popov E.S., Savinykh A.F. Simulation of the thermal conditions of rolls in a wide-strip hot-rolling mill to determine their effective cooling conditions. Russian Metallurgy (Metally). 2009;(3):208–219.
2. Bel’skii S.M., Mazur I.P., Astakhov A.A. Simplified computational procedure of thermal profiling of working rolls of hot-rolling mill. Proizvodstvo prokata. 2018;(2):3–6. (In Russ.).
3. Antonyuk V.V., Fedin A.G., Mustafin V.A., Dema R.R., Platov S.I., Amirov R.N., Koldin A.V. Kharchenko M.V. Setting up and controlling the thermal state of working rolls in the 2000 wide-strip hot-rolling mill of PJSC “Magnitogorsk Iron and Steel Works”. In: Proceedings of the XI Int. Congress of Rollers. Vol. 2. 2017. (In Russ.).
4. Garber E.A., Mishnev P.A., Shalaevskii D.L., Paligin R.B., Mikheeva I.A., Bolobanova N.L. New methods for modeling and reducing the non-flatness of steel strips during hot rolling on wide-strip mills. In: Proceedings of the Int. Sci. Seminar “Scientific and Technological Progress in Metallurgy – 2013”. 2014:70–82. (In Russ.).
5. Hamraoui M. Thermal behaviour of rollers during the rolling process. Applied Thermal Engineering. 2009;29(11–12): 2386–2390. https://doi.org/10.1016/j.applthermaleng.2008.12.013
6. Johnson R.E., Keanini R.G. An asymptotic model of work roll heat transfer in strip rolling. International Journal of Heat and Mass Transfer. 1995;41(6–7):871–879. https://doi.org/10.1016/S0017-9310(97)00175-0
7. Campos A.M., Garcia D.F., Usamentiaga R., de Abajo N., Gonzalez J.A. Real time model for the intelligent control of cooling systems for hot strip mill work rolls. 26th Annual Conference of the IEEE. 2000. https://doi.org/10.1109/IECON.2000.972272
8. Hlady C.O., Brimacombe J.K., Samarasekera I.V., Hawbolt E.B. Heat transfer in the hot rolling of the metal. Metallurgical and Material Transactions B. 1995;26:1019–1027. https://doi.org/10.1007/BF02654104
9. Zhang X.M., Yiang Z.Y., Tieau A.K., Liu X.N., Wang G.D. Numerical modeling of the thermal deformation of CVC work rolls in hot strip rolling. Journal of Material Processing Technology. 2002;130–131:219–223. https://doi.org/10.1016/S0924-0136(02)00736-7
10. Serajzadeh S., Karemi Taheri A., Mucciardi F. Unsteady state work-roll temperature distribution during continuous hot slab rolling. International Journal of Mechanical Sciences. 2002;44(12):2447–2462. https://doi.org/10.1016/S0020-7403(02)00179-0
11. Mercado-Solis R.D., Talamantes-Silva J., Beynon J.H., Hernandes-Rodrigues M.A.L. Modelling surface thermal damage to mill rolls. Wear. 2007;263(17–20):1560–1567. https://doi.org/10.1016/j.wear.2006.12.062
12. Hwang S.M., Sun C.G., Ryoo S.R., Kwak W.J. An itegrated FE process model for prevision analysis of the thermo-mechanical behaviours of rolls and strip in hot strip rolling. Computer Methods in Applied Mechanics and Engeneering. 2002;191:4015–4033. https://doi.org/10.1016/S0045-7825(02)00298-0
13. Kotrbacek P., Horsky J., Raudensky M., Pohanka M. Experimental study of heat transfer in hot rolling. Revue de Métallurgie. 2006;103(7–8):333–341. https://doi.org/10.1051/metal:2006134
14. Arif A.F., Khan O., Zubair S.M. Prediction of roll temperature with a non-uniform heat flux at tool and workpiece interface. Heat and Mass Transfer. 2004;41(1):75–94. https://doi.org/10.1007/s00231-004-0508-6
15. Garber E.A. Modeling and Improvement of Thermal Mode and Forming of Rolls: Monograph. Cherepovets: ChSU; Moscow: Teplotekhnik; 2013:114. (In Russ.).
16. Garber E.A., Khlopotin M.V., Savinykh A.F., Kozhevnikov A.V., Golovanov A.V., Smirnov V.S. Industrial tests of improved crowning of work rolls in wide-strip hot rolling mill. Proizvodstvo prokata. 2008;(4):18–22. (In Russ.).
17. Garber E.A., Khlopotin M.V., Popov E.S., Savinykh A.F., Golovanov A.V. Improving the efficiency of cooling rolls in a wide-strip hot rolling mill using adaptive mathematical models of heat balance. Proizvodstvo prokata. 2009;(4):12–24. (In Russ.).
18. Garber E.A. Cold Rolling Mills. Moscow: Chermetinformatsiya; 2004. (In Russ.).
19. Garber E.A., Mishnev P.A., Shalaevskii D.L., Paligin R.B., Mikheeva I.A., Bolobanova N.L. Modeling and reduction of strips non-flatness during hot rolling at the stage of setting up a wide-strip mill. Proizvodstvo prokata. 2014;(3):7–13. (In Russ.).
20. Shalaevskii D.L., Korepina K.P. Influence of cross profile of cold rolled strips on occurrence of flatness defects. Chernye metally. 2022;(3):56–59. (In Russ.).
About the Author
D. L. ShalaevskiiRussian Federation
Dmitrii L. Shalaevskii, Cand. Sci. (Eng.), Assist. Prof. of the Chair of Metallurgy, Mechanical Engineering and Technological Equipment
5 Lunacharskogo Ave., Cherepovets, Vologda Region 162600, Russian Federation
Review
For citations:
Shalaevskii D.L. Investigation of thermal mode of hot-rolling mill working rolls in order to improve the accuracy of calculating the thermal profile of their barrels’ surface. Izvestiya. Ferrous Metallurgy. 2023;66(3):283-289. https://doi.org/10.17073/0368-0797-2023-3-283-289