Calculation of temperature and thermoelastic stresses in strikers during production of hollow steel billets in a unit of combined casting and deformation. Part 2

Introduction

The main and most heavily loaded elements of a unit of combined casting and deformation are the strikers [1; 2]. During the working stroke, they simultaneously compress the wall of a steel hollow shell and move it in the casting direction. In this process, combined stresses arise in the strikers during the working stroke due to the compression force and the thermal load [3 – 5]. Therefore, a relevant problem is to substantiate the selection of the striker material that ensures the ability to withstand cyclic loading under the combined action of mechanical and thermoelastic stresses [6 – 8].

To calculate the stress state of the striker in the unit, its temperature field was first determined based on solving the unsteady thermal conductivity equation with the corresponding initial and boundary conditions [9 – 11].

The outer and inner diameters of the hollow billet made of 09G2S steel are 100 and 60 mm, respectively. The angular speed of the eccentric shafts was taken as 40 min^–1. At this speed, the contact time of the striker with the wall of the hollow billet during the working stroke is 0.375 s, and the pause time is 1.125 s. The temperature of the hollow billet in the striker entry zone is 1200 °С [12 – 14].

The geometry of the striker with dimensions is given in [9]. Iterative calculations showed that, to ensure a temperature of 350 °C on the striker contact surface at a heat transfer coefficient of 2000 W/(m²·K), the heat flux density is 4.6 MW/m² [15].

It was established that, under the action of heat flow during compression of the hollow billet wall by the strikers, the temperature on the striker contact surface lies in the range of 370 – 451 °C. Subsequently, during idle operation with water cooling, the temperature of the striker contact surface decreases and falls within the range of 289 – 370 °С.

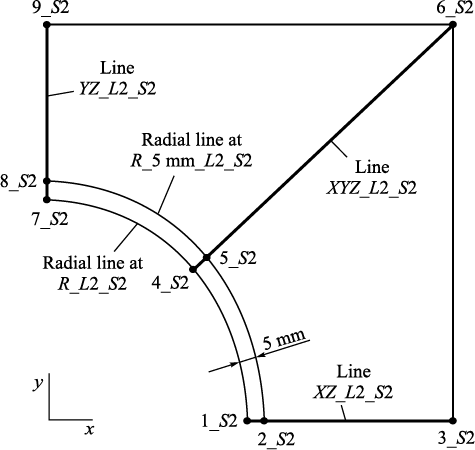
Based on the obtained temperature fields, thermoelastic stresses in the strikers of the unit were determined by the finite element method using the ANSYS package [16] (with elements of the calculation methodologies described in [16 – 18]). The finite element size in the deformation zone and in the calibrating sections of the strikers was taken as 1 mm. By symmetry, the calculation was performed for one half of the striker shown in Fig. 1 [9]. The calculation results for radial (SR), tangential (Sθ), axial (SZ), and equivalent (SEQV) thermoelastic stresses are presented only for the characteristic lines XZ_L2_S2, XYZ_L2_S2, and R_L2_S2 and for the points of section 2 associated with the striker contact surface (Fig. 1).

The Table presents the values of thermoelastic stresses at the points of the characteristic lines of section 2 under the action of heat flow (HF) and during water cooling (WC).

Fig. 2 shows the patterns of thermoelastic stress distribution in the strikers along the characteristic line R_L2_S2.

Let us consider the distribution of thermoelastic stresses in the strikers along the characteristic lines of section 2 (Fig. 1), where the maximum compressive stresses arise during compression of the wall of the steel hollow billet. Thus, at point 1_S2 of the XZ_L2_S2 line, which passes along the axis of symmetry of the striker caliber, at the contact surface, the maximum compressive axial stresses SZ reach −703 MPa (Fig. 2, Table).

During idle operation with water cooling, compressive thermoelastic stresses Sθ and SR at the striker contact surface at point 1_S2 are significantly lower and amount to −58 and −191 MPa, respectively (Fig. 2, Table).

It should be noted that along the XYZ_L2_S2 line, the compressive thermoelastic stresses Sθ and SZ at the striker contact surface during compression of the hollow billet wall are quite high; at point 4_S2, they are −381 and −652 MPa, respectively (Fig. 2, Table).

During idle operation, at the striker contact surface at point 4_S2, the tangential stresses Sθ are tensile, with a maximum value of 148 MPa, while the axial stresses SZ are compressive, with a value of –142 MPa. However, through the striker thickness, the axial stresses initially increase to –312 MPa, then decrease, change sign, and become tensile, reaching a maximum value of 141 MPa (see Table).

Let us consider the distribution of thermoelastic stresses along the radius of the striker contact surface (line R_L2_S2, Fig. 1).

During compression of the hollow billet wall, at point 1_S2 of the striker contact surface, the thermoelastic stresses Sθ and SZ are compressive, amounting to –589 and –703 MPa, respectively. Along the radius, they decrease and at point 4_S2 become –381 and –652 MPa, while at point 7_S2 they are –59 and –63 MPa, respectively (Fig. 2, Table).

During idle operation, at point 1_S2 of the striker contact surface, compressive thermoelastic stresses Sθ and SZ arise with values of –58 and –191 MPa, respectively. Further along the radius of the striker contact surface, at point 7_S2, they become tensile, reaching 25 and 341 MPa, respectively (Fig. 1, Table).

As a result of the study, it was established that the temperature of the striker contact surface during compression of the steel hollow billet wall can reach 451 °C. At this temperature, the compressive thermoelastic stresses at the striker contact surface reach 703 MPa.

The calculated values of thermoelastic stresses correlate well with the results obtained in similar studies using the QForm analysis software system [19].

Considering the above, the strikers of the unit of combined casting and deformation for producing steel hollow billets should be manufactured from 4Kh4VMFS steel. This is a die steel with increased resistance to heat checking and high wear resistance. The conditional yield strength of the steel at a temperature of 500 °C is 1309 MPa, which significantly exceeds the maximum thermoelastic stresses caused by the thermal load [20]. This steel is also used for manufacturing tooling for high-speed machine forging and upsetting on horizontal forging machines.

Conclusions

A procedure has been developed for calculating thermoelastic stresses in calibrated strikers of a unit of combined casting and deformation during the production of steel hollow pipe billets. The magnitudes and patterns of thermoelastic stress distribution in three sections of the calibrated striker during the production of steel hollow billets in a unit of combined casting and deformation have been determined. It has been established that the maximum compressive thermoelastic stresses at the striker contact surface reach 703 MPa. It is proposed that the strikers of the unit of combined casting and deformation for producing steel hollow billets be manufactured from 4Kh4VMFS steel, whose yield strength at a temperature of 500 °C is 1309 MPa.