Влияние кольцевых швов на напряженно-деформированное состояние в цилиндрической керамической оболочковой форме при затвердевании в ней стальной отливки

А. И. Евстигнеев; В. И. Одиноков; Д. В. Чернышова; А. А. Евстигнеева; Э. А. Дмитриев

doi:10.17073/0368-0797-2025-6-613-620

Влияние кольцевых швов на напряженно-деформированное состояние в цилиндрической керамической оболочковой форме при затвердевании в ней стальной отливки

А. И. Евстигнеев, В. И. Одиноков, Д. В. Чернышова, А. А. Евстигнеева, Э. А. Дмитриев

https://doi.org/10.17073/0368-0797-2025-6-613-620

Полный текст:

PDF (Rus) PDF (Eng) HTML (Eng) HTML XML (Eng) XML

сгенерировать QR код

Содержание

Перейти к:

Аннотация

При кристаллизации жидкого металла в оболочковой литейной форме на ее поверхностях возникают значительные нормальные напряжения: на внутренней – сжимающие, на наружной – растягивающие. Особенно ярко они проявляются в начальный момент времени охлаждения. Это может привести к повреждению литейной формы, а значит, и к повреждению кристаллизующейся металлической отливки. Снизить уровень напряженно-деформированного состояния в поверхностных слоях можно с помощью нанесения на внешнюю и внутреннюю поверхности специальных кольцевых (температурных) выточек (швов). В настоящей работе сформулирована и решена задача по влиянию температурных швов во внутренних и внешних слоях оболочковой формы (ОФ) на уровень её напряженно-деформированного состояния (НДС) при кристаллизации стальной отливки. В качестве параметра стойкости ОФ к трещинообразованию приняты нормальные напряжения σ₂₂, σ₃₃, возникающие как на внутренней, так и внешней поверхностях ОФ в начальный момент заливки металла и охлаждения стальной отливки. Рассматривается осесимметричная задача для цилиндрической керамической ОФ. На основе сформулированной целевой функции приведен алгоритм решения задачи с использованием уравнений линейной теории упругости, уравнения теплопроводности и апробированного численного метода. В результате решения задачи определено минимальное количество и места расположения выточек на внутренней и внешней поверхности ОФ, обеспечивающих уменьшение нормальных напряжений. Результаты решения задачи представлены в виде эпюр напряжений по сечениям рассматриваемой области. Дан анализ полученных результатов стойкости ОФ к трещинообразованию. Даны рекомендации по использованию результатов работы в различных научно-технических областях.

Ключевые слова

литье по выплавляемым моделям, оболочковая форма, напряженное состояние, температурный шов, трещиностойкость, алгоритм определения напряжений

Для цитирования:

Евстигнеев А.И., Одиноков В.И., Чернышова Д.В., Евстигнеева А.А., Дмитриев Э.А. Влияние кольцевых швов на напряженно-деформированное состояние в цилиндрической керамической оболочковой форме при затвердевании в ней стальной отливки. Известия высших учебных заведений. Черная Металлургия. 2025;68(6):613-620. https://doi.org/10.17073/0368-0797-2025-6-613-620

For citation:

Evstigneev A.I., Odinokov V.I., Chernyshova D.V., Evstigneeva A.A., Dmitriev E.A. Effect of annular seams on stress-strain state in cylindrical ceramic shell mold during solidification of a steel casting in it. Izvestiya. Ferrous Metallurgy. 2025;68(6):613-620. https://doi.org/10.17073/0368-0797-2025-6-613-620

Введение

Литье по выплавляемым моделям остается одной из самых востребованных технологий получения отливок высокой геометрической сложности с сохранением требуемой точности.

Недостатком этого метода литья является высокий процент брака оболочковых форм (ОФ), что связано с образованием микро- или макротрещин в них, их частичным или полным разрушением в процессе формообразования, а, главным образом, на технологических операциях (прокаливании, заливки их расплавом в начальной стадии охлаждения отливки) из-за неравномерного нагрева по толщине литейной ОФ. Такая низкая стойкость ОФ связана с повышенным уровнем напряженно-деформированного состояния (НДС) в них. Для снижения влияния таких воздействий в производстве применяют различные технологические решения.

Вопросам исследования НДС литейных многослойных оболочковых форм посвящены работы как отечественных, так и зарубежных исследователей. Так, в работах [1; 2] отражено влияние формы и геометрии ОФ, в работах [3; 4] – толщины стенки ОФ, в работах [5; 6] – материала формы, а в работах [7 – 9] – геометрии отливки. Отечественные исследования, посвященные рассматриваемой проблеме, представлены в работах [10 – 13]. Аналогичные проблемы изучались и при литье в кокиль [14; 15].

Настоящая работа является продолжением исследований авторов по трещиностойкости керамической ОФ по выплавляемым моделям при получении в ней металлических отливок. В ранних работах авторов с помощью математического моделирования изучалось НДС цилиндрических ОФ при заливке их жидким металлом. В результате теоретического анализа были найдены оптимальные физические параметры материала ОФ и ее морфологической структуры, оказывающие решающее влияние на трещиностойкость. Эти исследования легли в основу разработанных новых видов (типов, образцов) ОФ, по которым получены патенты РФ на изобретения (№ 2743439, № 2763359) и др.

В основу теоретических исследований авторов положен численный метод [16], с помощью которого решаются задачи в следующей постановке: жидкий металл заливается в многослойную ОФ, в которой он затвердевает в виде отливок; в процессе охлаждения отливки определяется НДС и температура в сечениях ОФ.

На начальном этапе исследования проводились на отливке в виде цилиндра со сферическим закруглением в данной части, что имитирует модель отливки в виде стояка в ОФ.

Дальнейшие теоретические исследования цилиндрических ОФ были связаны с установлением влияния силового воздействия опорного наполнителя (ОН) и параметров межслойного трения в ОФ на ее НДС [17; 18], по результатам которых также получены патенты (№ 2769192, № 2788296).

Как показал производственный опыт контроля стойкости литейных форм, наиболее непредсказуемой формой получаемой отливки является сферическая или шарообразная. Для таких ОФ определен оптимальный угол их охвата опорным наполнителем и его влияние на уровень НДС в ОФ [19].

Математическое моделирование таких процессов с использованием численных методов представлено в зарубежных работах [20 – 22], а моделирование НДС в затвердевающей отливке – в работах [23; 24].

Поиск новых технологических решений по снижению критического уровня НДС в ОФ позволил предложить новую конструкцию литейной керамической ОФ [25], основанную на известном методе снижения параметров термических напряжений в отливках за счет применения так называемых «ребер жесткости» [26].

Выявлено повышение стойкости сферической литейной ОФ за счет наличия на внутренней поверхности формы кольцевых (температурных) швов или выточек. Повышение стойкости при наличии таких швов установлено и в металлических литейных формах.

Отметим, что при заливке стали в ОФ сферической геометрии внутренние нормальные напряжения в сечении полностью сжимающие, причем довольно большой величины, в связи с чем теоретические исследования сводились к поиску условий, способствующих уменьшению (по модулю) этих напряжений. Наиболее эффективной оказалась конструкция литейной формы с кольцевыми швами в облицовочном слое [25]. В литейных формах цилиндрической конфигурации наибольшую опасность представляют растягивающие нормальные напряжения на поверхности соприкосновения формы с ОН.

В настоящей работе рассматривается литейная керамическая форма с цилиндрическим участком и теоретически анализируется влияние температурных швов не только на внешнем слое ОФ, но и на внутренней ее поверхности. Рассматривается «жесткий» вариант литейной формы: монослойная керамическая с постоянным модулем сдвига.

Математическая постановка задачи

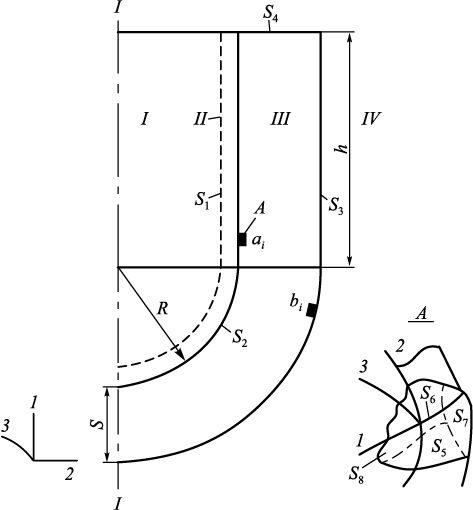
Рассматривается осесимметричное тело вращения (рис. 1), имеющее жидкую фазу (металл) (I), затвердевающую корочку (II), оболочковую форму (III), опорный наполнитель (IV), круговые выточки a_i на поверхности облицовочного слоя (поверхности S₂) и круговые выточки b_i на поверхности соприкосновения формы (III) с опорным наполнителем (IV) (поверхности S₃).

Рис. 1. Расчетная схема системы с указанием поверхности к граничным условиям задачи:
S₁ – поверхность контакта жидкого и затвердевшего металла;
S₂ – внутренняя поверхность контакта затвердевшего металла и керамической формы;
S₃ – внешняя поверхность контакта керамической формы с опорным наполнителем;
I – жидкий металл; II – корочка затвердевшего металла;
III – оболочковая форма; IV – опорный наполнитель;
R – радиус сферической части ОФ; h – высота цилиндрической части ОФ

Пусть А – конечное множество круговых выточек a_i на поверхности S₂; A = {a_i, i = 1, ..., n}; В – конечное множество круговых выточек b_i на поверхности S₃; B = {b_k, k = 1, ..., m}. Положим, C = A \( \cup \) B. Как следует из многочисленных работ авторов, опасными напряжениями при заливке стали в ОФ являются σ₂₂, σ₃₃. Причем при охлаждении стали в ОФ с цилиндрическими участками опасными являются растягивающие напряжения σ₂₂ на поверхности S₃, а при охлаждении стали в ОФ сферической конфигурации опасными являются сжимающие напряжения σ₃₃ на поверхности S₂.

Сформулируем задачу.

Требуется найти такое наименьшее количество выточек А на поверхности S₂ ОФ и количество выточек В на поверхности S₃, а также их геометрическое расположение, чтобы при охлаждении металла в литейной форме (ЛФ) наибольшие (по модулю) напряжения в области Q при τ = τ^* не превышали заданных ограничений:

\[\begin{array}{c}\left| {{\sigma _{33}}} \right| < 55{\rm{ МПа}};\\{\sigma _{22}} < 20{\rm{ МПа}},\end{array}\]

(1)

здесь Q – область меридианного сечения; τ^* – максимальное время охлаждения, после которого температура по области Q начинает выравниваться и нормальные напряжения σ₂₂, σ₃₃ начинают уменьшаться (по модулю).

Значение τ^* определим из функции

\[F = \max \left| {{\sigma _{33}}(\tau ,Q)} \right|,\]

(2)

при ограничении τ ≤ 60 с.

Для определения F запишем систему уравнений в декартовой системе координат для каждой из подобластей (рис. 1), используя линейную теорию упругости:

– область I:

\[\begin{array}{c}{\sigma _{11}} = {\sigma _{22}} = {\sigma _{33}} = \sigma = {P_1};\\{P_1} = - \gamma h;{\rm{ }}\dot \theta = {a_1}\Delta \theta ;\end{array}\]

(3)

– области II, III:

\[\left\{ \begin{array}{l}{\sigma _{ij,j}} = 0,{\rm{ }}i,j = 1,{\rm{ }}2,{\rm{ }}3;\\{s_{ij}} - \sigma {\delta _{ij}} = 2{G_p}\varepsilon _{ij}^*;{\rm{ }}\varepsilon _{ij}^* = {\varepsilon _{ij}} - \frac{1}{3}\varepsilon {\delta _{ij}};{\rm{ }}\varepsilon = {\varepsilon _{ii}};\\{\varepsilon _{ii}} = 3{k_p}\sigma + 3{\alpha _p}\left( {\theta - \theta _p^*} \right);{\rm{ }}{\varepsilon _{ij}} = 0,5\left( {{U_{i,j}} + {U_{j,i}}} \right);\\{C_p}\gamma \frac{{\partial \theta }}{{\partial \tau }} = {\rm{div}}(\lambda {\rm{grad}}\theta ),\end{array} \right.\]

(4)

где σ_ij – компоненты тензора напряжений; σ – гидростатическое напряжение; ε_ij – компоненты тензора упругих деформаций; h – высота столба жидкого металла; \({k_p} = \frac{{1 - 2\mu }}{E}\) – коэффициент объемного сжатия; μ – коэффициент Пуассона; E – модуль Юнга; G_p(θ) – модуль сдвига в области p (p = II, III); α_p – коэффициент линейного расширения; a₁ – коэффициент температуропроводности в области (I); τ – время; θ – температура; C_p – удельная теплоемкость в области (p); γ – удельный вес; \(\theta _p^*\) – начальная температура в области (p); λ = λ (θ) – коэффициент теплопроводности; используется суммирование по повторяющимся индексам.

В процессе охлаждения жидкого металла при условии, что температура металла θ_м ≤ θ_к (θ_к – температура кристаллизации), определяется толщина затвердевшего слоя Δ_i из решения уравнения межфазового перехода.

Начальные условия задачи:

\({\left. \Delta \right|_{\tau = 0}} = 0\) – отсутствие твердой фазы металла;

\({\left. {\theta _I^*} \right|_{\tau = 0}} = \theta _{\rm{м}}^*\) – температура разливаемого жидкого металла;

\({\left. {\theta _{III}^*} \right|_{\tau = 0}} = {\theta ^*}\) – начальная температура формы.

Граничные условия задачи в ортогональных координатах (рис. 1):

– для осесимметричной задачи

\[\begin{array}{c}{U_3} = 0;{\rm{ }}{\sigma _{31}} = {\sigma _{32}} = 0;{\rm{ }}{\varepsilon _{13}} = {\varepsilon _{23}} = 0;\\\frac{{\partial {u_i}}}{{\partial {x_3}}} = 0;{\rm{ }}\frac{{\partial {\sigma _{3i}}}}{{\partial {x_3}}} = 0,{\rm{ }}i = 1,{\rm{ }}2,{\rm{ }}3;\end{array}\]

(5)

– на оси симметрии

U₂ = 0; σ₂₁ = 0; q_n = 0; θ = θ_м;

– на поверхностях S₁, S₃, S₄

\[\begin{array}{c}{\left. {{\sigma _{11}}} \right|_{{S_1}}} = - P;{\rm{ }}{\left. {{\sigma _{12}}} \right|_{{S_1}}} = 0;{\rm{ }}{\left. {{U_1}} \right|_{{{S'}_3}}} = 0;{\left. {{\rm{ }}{\sigma _{21}}} \right|_{{S_4}}} = 0;\\{\left. {{\sigma _{22}}} \right|_{{S_4}}} = 0;{\rm{ }}{\left. {{\sigma _{11}}} \right|_{{{S''}_3}}} = 0;{\rm{ }}\\{\left. {{\sigma _{12}}} \right|_{{{S'}_3}}} = - \psi \frac{{{U_{{\rm{ск}}}}}}{{{U^*}}}{\tau _s}\cos ({n_1}{x_1});{\rm{ }}\\{\left. \theta \right|_{{S_3}}} = {\theta ^*};{\rm{ }}{\left. \theta \right|_{{S_2}}} = {\theta _{\rm{м}}},\end{array}\]

(6)

где U_ск – перемещение материала формы при скольжении относительно ОН (песка), U^* – нормирующее перемещение; ψ – параметр, характеризующий условия трения между формой и опорным наполнителем; τ_s – условный предел текучести при сдвиге; q_n – тепловой поток.

При решении температурной задачи использовались граничные условия первого рода. Для определения θ_м(τ) и θ^*(τ) воспользуемся данными работы [27]:

\[\begin{array}{c}{\theta _{\rm{м}}} = \theta _{\rm{м}}^* - \frac{\tau }{{{\tau _1}}}{\theta _1};\\0 < \tau < 60{\rm{ c}};\\{\theta ^*} = {\theta _0}\left( {1 + \sqrt {\frac{\tau }{{{\tau _2}}}} } \right),\end{array}\]

(7)

здесь τ – время охлаждения, с; \(\theta _{\rm{м}}^*\) = 1550 °С; θ₁ = 100 °C; θ₀ = 20 °С; θ^* – температура на поверхности S₃; τ₁ = 60 с; τ₁ = 1 с.

Время τ не превышает 60 с, так как при τ ≥ 60 с напряжения в ОФ не представляют опасности разрушения.

Примем модуль сдвига ОФ

G_ф = 2960 кг/мм².

(8)

Алгоритм решения системы (4) при граничных условиях (5) – (7) подробно описан в работе [27].

Расчет показал следующее:

F = –65,6 МПа; τ^x = 21,65 с.

(9)

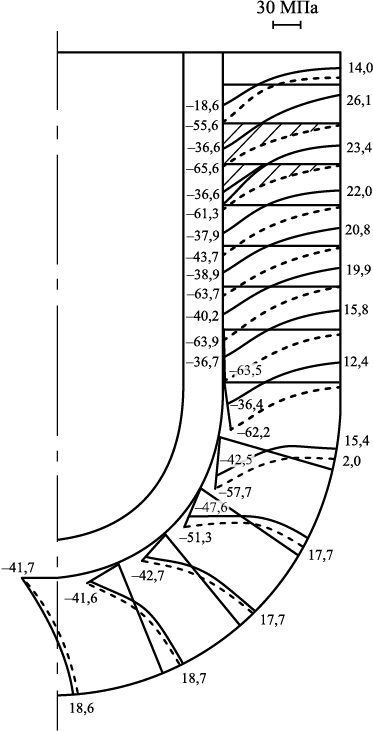
Результат решения приведен на рис. 2 в виде эпюр по сечению рассматриваемой оболочки. Напряжения σ₂₂, σ₃₃ весьма значимы. На облицовочном слое σ₂₂, σ₃₃ отрицательны и достигают значительной величины на цилиндрической части ОФ, причем |σ₃₃| > |σ₂₂| в 1,5 раза. На сферической части σ₂₂ и σ₃₃ меньше отличаются, но, приближаясь к цилиндрической области, разница между ними весьма значительна. На наружном слое (контакте с опорным наполнителем) напряжения σ₂₂ положительны. Причем на сферической части примерно одинаковой величины, а на цилиндрической – возрастают к верхней части формы. Напряжения σ₃₃ на этой поверхности (поверхность S₃) сопоставимы с напряжением σ₂₂ в сферической части и практически равны нулю на цилиндрической. Из рис. 2 видим, что напряжения σ₃₃, σ₂₂ при заливке стали в керамическую форму значительно превосходят (по модулю) ограничения (1).

Рис. 2. Эпюры напряжений σ₂₂ () и σ₃₃ () по сечению ОФ

Зная значения τ^* (9), перейдем к решению поставленной задачи. Рассматривается процесс охлаждения стали в керамической форме с температурными швами (круговыми выточками). В отличие от предыдущей задачи сечение Q представляет многосвязную область. Начальные и граничные условия во многом совпадают с предыдущей задачей. Граничные условия (6) дополняются (рис. 1):

\[{\left. {({\sigma _{22}} = {\sigma _{21}})} \right|_{{S_i}}} = 0,{\rm{ }}i = 5,{\rm{ }}6;{\left. {{\rm{ }}({\sigma _{11}} = {\sigma _{12}})} \right|_{{S_i}}} = 0,{\rm{ }}i = 7,{\rm{ }}8;\]

(10)

Выполняется также соотношение (7) при принятом значении модуля сдвига (8).

Алгоритм решения задачи

1. Задаются геометрические размеры области, конечное время охлаждения τ^*, геометрические размеры выточек и их начальные координаты на S₂, S₃: a_i(0), b_i(0). Время охлаждения τ^* разбивается на конечное число шагов: \({\tau ^*} = \sum {\Delta {\tau _n}} \) (где n – номер временного шага).

2. Исследуемая область разбивается системой ортогональных поверхностей на конечное число элементов.

3. Вычисляются длины дуг элементов \(S_{ij}^k\) (i, k = 1, 2, 3; i ≠ k; j = 1, 2).

4. Задаются начальные и граничные условия по элементам, образующим рассматриваемую область (5), (6), (10), и константы физико-механических свойств материалов.

5. Определяется поле температур на временном шаге Δτ_n численным решением уравнения теплопроводности с использованием итерационной формулы [27], при наличии начальных и граничных условий на данном временном шаге. Наличие выточек при решении температурной задачи не учитывалось.

6. Если выполняется условие \({\left. \theta \right|_{{S_2}}} \le {\theta _{\rm{}}}\) области (I) у поверхности S₂, то вычисляется толщина закристаллизовавшейся корочки Δ_n.

7. Решается система уравнений (3), (4) с учетом граничных условий (6), (10), разностных аналогов и разработанной методики с использованием программы «Одиссей»¹. Определяются поля напряжений σ_ij и перемещений U_i (i, j = 1, 2).

8. На поверхности S₃ проводится оценка прилегания формы к ОН по каждому элементу: если \({\left. {{\sigma _{11}}} \right|_{{S_3}}} > 0 \Rightarrow {\sigma _{11}} = 0,{\rm{ }}{\sigma _{12}} = 0\), проводится переназначение граничных условий и выполняется операция 7.

9. Проводится шаг по времени. По формулам (7) уточняются граничные условия решения температурной задачи. Если \(\sum {\Delta {\tau _n}} < {\tau ^*}\), то выполняется операция 5. Если \(\sum {\Delta {\tau _n}} = {\tau ^*}\), то выполняется операция 10.

10. По области Q анализируются значения σ₃₃, σ₂₂ и выбираются наибольшие (по модулю) значения, превосходящие ограничения (1). Формируются матрицы \([{\bar \sigma _{22}}],{\rm{ }}[{\bar \sigma _{33}}]\). Если ограничения (1) выполняются, то следует операция 12.

11. Из матрицы \([{\bar \sigma _{22}}],{\rm{ }}[{\bar \sigma _{33}}]\) выбираются наибольшие, и в этих сечениях выполняются выточки. Выполняется операция 7.

12. Процесс расчета заканчивается.

Результаты решения задачи

Геометрические параметры: S = 5 мм; R = 20 мм; h = 50 мм.

Временные интервалы Δτ_n: 0,01, 0,02, 0,03, 0,04, 0,05, 0,1, 0,2, 0,3, 0,4, 0,5, 2, 5, 5, 5, 3, 3, 5, 5, 5, 5 с.

Приняты следующие физические параметры разливаемой стали при θ > 1000 °C (\(\theta _{\rm{м}}^*\) = 1550 °С) [27]:

G = 1000 кг/мм²; α = 12·10^–6 град^–1;

λ = 0,0298 Вт/(мм·°C);

L = 270·10³ Дж/кг (скрытая теплота плавления);

C = 444 Дж/(кг·°C); γ = 7,80·10^–6 кг/мм³; θ_к = 1450 °C.

Физические свойства керамической формы:

G = 2960 кг/мм²; α = 0,51·10^–6 град^–1;

λ = 0,000812 Вт/(мм·°C);

C = 840 Дж/(кг·°C); γ = 2,0·10^–6 кг/мм³.

Размеры выточек: a_i = 1×2 мм, b_i = 1×3 мм.

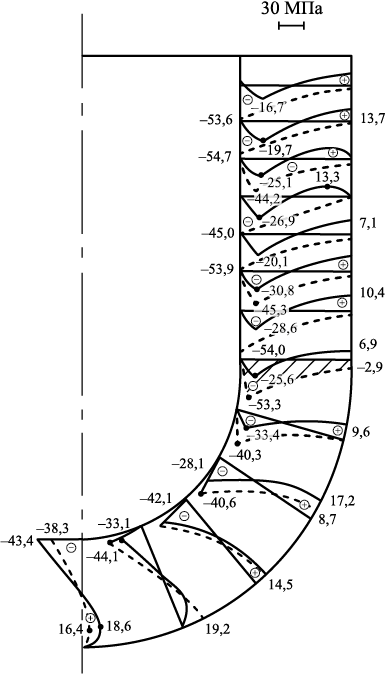
Расчет по приведенному выше алгоритму показал следующие значения: F = 5; a_i = 2; b_i = 3; геометрическое местоположение выточек (a_i, b_i) и температуры в сечении (x₂ = 0) показаны на рис. 3. Полученные результаты по напряжениям σ₃₃, σ₂₂ приведены на рис. 4.

Рис. 3. Расчетная схема системы с группой выточек
на облицовочном и наружном слоях ОФ

Рис. 4. Эпюры напряжений σ₂₂ () и σ₃₃ () по сечению ОФ

Видим, что все максимальные значения напряжений σ₃₃ (по модулю) и растягивающие напряжения σ₂₂ отвечают заданным ограничениям (1), хотя и очень близки в некоторых сечениях к граничным величинам.

Выводы

Поставлена и решена осесимметричная задача по оптимизации процесса охлаждения стальной отливки в керамической форме, имеющей цилиндрический и сферический участки и температурные кольцевые вырезы.

Показана эффективность нанесения на литейную форму кольцевых выточек на наружную и внутреннюю поверхности, соприкасающиеся с охлажденным металлом.

Полученные результаты могут быть полезны при исследованиях других технологических процессов, проведении прочностных расчетов и решении оптимизационных задач.

Список литературы

1. Kanyo J.E., Schafföner S., Uwanyuze R.Sh., Leary K.S. An overview of ceramic molds for investment casting of nickel superalloys. Journal of the European Ceramic Society. 2020;40(15):4955–4973. https://doi.org/10.1016/j.jeurceramsoc.2020.07.013

2. Rafique M.M.A., Iqbal J. Modeling and simulation of heat transfer phenomena during investment casting. International Journal of Heat and Mass Transfer. 2009;52(7-8):2132–2139. http://doi.org/10.1016/j.ijheatmasstransfer.2008.11.007

3. Singh R. Mathematical modeling for surface hardness in investment casting applications. Journal of Mechanical Science and Technology. 2012;26:3625–3629. http://dx.doi.org/10.1007/s12206-012-0854-0

4. Jafari H., Idris M.H., Ourdjini A. Effect of thickness and permeability of ceramic shell mould on in situ melted AZ91D investment casting. Applied Mechanics and Materials. 2014;465-466:1087–1092. http://dx.doi.org/10.4028/www.scientific.net/AMM.465-466.1087

5. Bansode S.N., Phalle V.M., Mantha S. Taguchi approach for optimization of parameters that reduce dimensional variation in investment casting. Archives of Foundry Engineering. 2019;19(1):5–12. https://dx.doi.org/10.24425/afe.2018.125183

6. Pattnaik S., Karunakar D.B., Jha P.K. Developments in investment casting process ‒ A review. Journal of Materials Processing Technology. 2012;212(11):2332–2348. https://doi.org/10.1016/j.jmatprotec.2012.06.003

7. Zhang J., Li K.W., Ye H.W., Zhang D.Q., Wu P.W. Numerical simulation of solidification process for impeller investment casting. Applied Mechanics and Materials. 2011; 80-81:961–964. https://doi.org/10.4028/www.scientific.net/AMM.80-81.961

8. Dong Y.W., Li X.L., Zhao Q., Yang J., Dao M. Modeling of shrinkage during investment casting of thin walled hollow turbine blades. Journal of Materials Processing Technology. 2017;244:190–203. https://doi.org/10.1016/j.jmatprotec.2017.01.005

9. Rakoczy Ł., Cygan R. Analysis of temperature distribution in shell mould during thin-wall superalloy casting and its effect on the resultant microstructure. Archives of Civil and Mechanical Engineering. 2018;18(4):1441–1450. https://doi.org/10.1016/j.acme.2018.05.008

10. Голенков Ю.В., Рыбкин В.А., Юсипов Р.Ф. Силовое взаимодействие опорного материала с оболочкой формы при литье по выплавляемым моделям. Литейное производство. 1988;(2):14–15.

11. Шпиндлер С.С., Неуструев А.А., Церельман Н.М. Определение термического сопротивления контакта отливка-форма при литье по выплавляемым моделям. Известия вузов. Черная металлургия. 1986;29(9):97–100.

12. Васин Ю.П., Лонзингер В.А. Расчет термостойкости оболочек при литье по выплавляемым моделям. Литейное производство. 1987;(2):19–21.

13. Тимофеев Г.И., Огорельцев В.П., Черепнин А.Ю. Влияние температурного фактора на напряженно-деформированное состояние оболочковой формы. Известия вузов. Черная металлургия. 1990;33(8):69–71.

14. Голофаев А.Н. Расчет напряженно-деформированного состояния кокилей методом конечных элементов. Литейное производство. 1983;(5):16.

15. Дембовский В.В. Численное моделирование процессов формирования отливок в металлических формах. Литейное производство. 1992;(6):31–32.

16. Математическое моделирование сложных технологических процессов / В.И. Одиноков, Б.Г. Каплунов, А.В. Песков, А.В. Баков. Москва: Наука; 2008:178.

17. Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Чернышова Д.В., Евстигнеева А.А. Влияние опорного наполнителя и структуры оболочковой формы на ее трещиностойкость. Известия вузов. Черная металлургия. 2022;65(4):285–293. https://doi.org/10.17073/0368-0797-2022-4-285-293

18. Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Чернышова Д.В., Евстигнеева А.А. Морфологическое строение оболочковой формы по выплавляемым моделям. Известия вузов. Черная металлургия. 2022;65(10):740–747. https://doi.org/10.17073/0368-0797-2022-10-740-747

19. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И., Намоконов А.Н., Чернышова Д.В., Евстигнеева А.А. Моделирование напряженно-деформированного состояния и оптимизация угла охвата сферической оболочковой формы опорным наполнителем. Прикладная механика и техническая физика. 2025;66(1(389)):189–196. https://doi.org/10.15372/PMTF202415455

20. Sabau A.S. Numerical simulation of the investment casting process. Transactions of American Foundry Society. 2005;113:407–417.

21. Zheng K., Lin Y., Chen W., Liu L. Numerical simulation and optimization of casting process of copper alloy water-meter shell. Advances in Mechanical Engineering. 2020;12(5): 1–12. http://dx.doi.org/10.1177/1687814020923450

22. Manzari M.T., Gethin D.T., Lewis R.W. Optimisation of heat transfer between casting and mould. International Journal of Cast Metals Research. 2000;13(4):199–206. https://doi.org/10.1080/13640461.2000.11819402

23. Огородникова О.М. Напряженно-деформированное состояние металла в эффективном интервале кристаллизации. Литейное производство. 2012;(9):21–24.

24. Десницкая Л.В., Десницкий В.В., Матвеев И.А. Учет напряженно-деформированного состояния кристаллизующихся стальных отливок в технологии их производства. Литейное производство. 2019;(4):6–8.

25. Патент RU № 2828801 РФ, МПК B22C 9/04 (2006.01), B22C 9/08 (2006.01). Литейная многослойная оболочковая форма / В.И. Одиноков, А.И. Евстигнеев, Э.А. Дмитриев, А.А. Евстигнеева, Д.В. Чернышова, Ю.И. Ткачева, А.Н. Намоконов. Заявл. 05.03.2024; опубл. 21.10.2024. Бюл. № 30.

26. Литейное производство: Учебник для металлургических специальностей вузов: под общ. ред А.М. Михайлова. Москва: Машиностроение; 1987:256.

27. Математическое моделирование процессов получения отливок в керамические оболочковые формы / В.И. Одиноков, Э.А. Дмитриев, А.И. Евстигнеев, В.И. Свиридов. Москва: Инновационное машиностроение; 2020:221.