Перейти к:
Вязкость жидких сплавов кобальта с кремнием и бором: эксперимент и расчет
https://doi.org/10.17073/0368-0797-2025-5-517-525
Аннотация
Методом крутильных колебаний проведены исследования температурных (до 1700 °С) и концентрационных зависимостей вязкости жидких бинарных сплавов кобальта с кремнием и бором. Температурные зависимости вязкости жидкого кобальта и его расплавов с кремнием и бором (до 54 ат. % металлоида) имеют монотонный характер без каких-либо особенностей и хорошо описываются уравнением Аррениуса. Совпадение политерм вязкости, полученных в режиме нагрева и охлаждения, а также линейная зависимость логарифма вязкости от обратной абсолютной температуры в переохлажденной области свидетельствуют о сохранении структуры жидкого сплава. Микронеоднородное строение расплавов Co – Si и Co – B (до 54 ат. % металлоида), связанное с образованием микрогруппировок на основе силицидов и боридов кобальта с более прочными внутренними связями, приводит к сложному виду концентрационных зависимостей их вязкости и энергии активации вязкого течения. В статье авторы обсуждают прогностические возможности уравнений Козлова-Романова-Петрова и Kaptay для описания концентрационных зависимостей вязкости жидких сплавов типа металл–металлоид. Рассмотрены особенности, связанные с применением этих уравнений к системам, в которых один из компонентов сплава (в данном случае бор в системе Co – B) при температурах расчета находится в твердом состоянии. Показано, что корректным способом решения проблемы является использование значения вязкости жидкого бора при его температуре плавления в качестве входного параметра для расчета изотерм вязкости расплавов системы Co – B. Уравнения Козлова-Романова-Петрова и Kaptay отличаются только коэффициентами перед энтальпией смешения расплава, физический смысл которых обсуждается в работе. Уравнение Козлова-Романова-Петрова может быть рекомендовано для прогнозирования концентрационных зависимостей вязкости жидких сплавов кобальта с кремнием и бором.
Ключевые слова
Для цитирования:
Олянина Н.В., Бельтюков А.Л., Ладьянов В.И. Вязкость жидких сплавов кобальта с кремнием и бором: эксперимент и расчет. Известия высших учебных заведений. Черная Металлургия. 2025;68(5):517-525. https://doi.org/10.17073/0368-0797-2025-5-517-525
For citation:
Olyanina N.V., Beltyukov A.L., Ladyanov V.I. Viscosity of liquid alloys of cobalt with silicon and boron: Experiment and calculation. Izvestiya. Ferrous Metallurgy. 2025;68(5):517-525. https://doi.org/10.17073/0368-0797-2025-5-517-525
Введение
Вязкость является важным физическим свойством жидкости, которое определяется межчастичным взаимодействием и связано с ее структурой. Поэтому вязкость часто используется для изучения строения высокотемпературных металлических расплавов. Особенно это актуально для систем металл–металлоид, для которых прямые дифракционные исследования проведены только на отдельных сплавах [1] или с небольшим перегревом над линией ликвидуса [2], а из-за смешения металлических и ковалентных типов связи использование методов моделирования для этих систем является до сих пор сложной задачей [3; 4].
Значения вязкости жидкости как физического свойства необходимы для многих металлургических процессов, связанных с жидким состоянием вещества [5 – 7]. Для прогнозирования вязкости многокомпонентных жидких сплавов используются уравнения, в частности уравнения Козлова-Романова-Петрова [8] и Kaptay [9], полученные с использованием термодинамического подхода. Необходимыми входными данными в уравнениях являются значения вязкости жидких чистых компонентов, которые составляют расплав, и энтальпии образования жидкого сплава. Указанные уравнения, согласно работе [10], хорошо прогнозируют концентрационные зависимости вязкости жидких сплавов с разными диаграммами состояния. Однако апробация проведена в основном на системах типа металл–металл. В состав же многих перспективных материалов входят металлоиды, а также элементы с высокой температурой плавления, такие как бор, тантал, ниобий. Наличие тугоплавких элементов затрудняет их применение к таким системам, поскольку расчет вязкости проводится при температурах, когда эти элементы находятся в твердом состоянии.
В настоящей работе представлены результаты экспериментальных исследований вязкости жидких сплавов систем Co – Si и Co – B и проведен анализ применимости уравнений Козлова-Романова-Петрова и Kaptay для прогнозирования их концентрационной зависимости.
Материалы и методика измерения
Лигатуры Со – Si и Со – B (54 ат. % металлоида) выплавляли в вакуумной печи сопротивления сплавлением порошка кобальта марки ПК-1у по ГОСТ 9721–79 (массовое содержание кобальта не менее 99,35 %; основные примеси, мас. %: менее 0,2 Fe; 0,4 Ni; 0,02 Si и C; 0,04 Cu) с монокристаллическим кремнием (99,9999 мас. % Si) или аморфным бором по ТУ 113–12–132–83 (94 мас. % В; основные примеси, мас. %: 0,23 Fe; 0,1 Si) в корундовом тигле при давлении 10–2 Па, температуре 1550 °С и выдержке 20 мин. Образцы необходимого состава получали сплавлением кобальта марки К0 по ГОСТ 123–2008 (массовое содержание кобальта не менее 99,98 %; основные примеси, мас. %: менее 0,003 Fe; менее 0,005 Ni и C; до 0,001 Si, Cu, Mg, Zn и Al) и лигатур Со – Si или Со – B в печи вискозиметра до проведения измерения по вязкости.
Кинематическую вязкость (ν) жидких сплавов измеряли на автоматизированной установке [11] методом затухающих крутильных колебаний тигля с расплавом в варианте Швидковского [12]. Эксперименты проводили в защитной атмосфере гелия марки А с предварительным вакуумированием рабочей камеры до давления 10–2 Па. Измерения вязкости осуществляли в режиме нагрева и последующего охлаждения со ступенчатым изменением температуры с шагом 20 – 30 °С после изотермических выдержек на каждой температуре в течение 10 мин. Исследования проводили в цилиндрических тиглях из Al2O3 с двумя торцевыми поверхностями трения (дно тигля и крышка на поверхности расплава). Для создания второй торцевой поверхности в тигель поверх образца устанавливали крышку с внешним диаметром на 0,5 – 0,8 мм меньше внутреннего диаметра тигля. Конструкция крышки [13; 14] позволяет ей свободно перемещаться вдоль вертикальной оси тигля и двигаться вместе с ним при возникновении крутильных колебаний подвесной системы. Применение двух торцевых поверхностей трения позволяет учесть неопределенности, которые вносят в расчет вязкости возможность образования оксидной пленки на поверхности расплава [13; 15] и эффект смачивания жидким металлом стенок тигля (наличие мениска) [16; 17]. Перед проведением измерений вязкости образцы подвергались переплаву при 1680 °С в течение 10 мин. Это позволяет исключить влияние на результаты измерения необратимых процессов, обусловленных сплавлением исходных шихтовых материалов. Общая ошибка определения вязкости для доверительной вероятности 0,95 не превышает 4 % при ошибке единичного эксперимента 1,5 %. Расчет ошибок проведен по методике, описанной в работе [11].
Для вычисления динамической вязкости (η) использовались литературные данные по плотности [18 – 20].
Уравнения для расчета вязкости
Уравнение Козлова-Романова-Петрова [8] было выведено в рамках теории осцилляторных жидкостей путем соотнесения колебательных движений атомов со свободной энергией раствора с помощью приближения Эйнштейна и имеет следующий вид:
| \[\ln \eta = {x_1}\ln {\eta _1} + {x_2}\ln {\eta _2} - \frac{{\Delta H}}{{3RT}},\] | (1) |
где η и ηi – динамическая вязкость расплава и его чистых компонентов (i = 1, 2) соответственно; xi – мольная доля компонента i в сплаве; ΔH – интегральная энтальпия образования (смешения) расплава; R – универсальная газовая постоянная; T – абсолютная температура.
Уравнение Kaptay [9] является модификацией уравнения Эйринга [21] на многокомпонентные сплавы и имеет следующий вид:
| \[\eta = \frac{{h{N_A}}}{{\sum\limits_{i = 1}^2 {\left( {{x_i}{V_i}} \right)} + {V^E}}}\exp \left( {\frac{{\sum\limits_{i = 1}^2 {\left( {{x_i}\Delta G_i^*} \right)} - \alpha \Delta H}}{{RT}}} \right),\] | (2) |
где Vi – молярный объем чистого компонента i в жидком состоянии (Vi = Mi /ρi , где ρi – плотность чистого компонента i в жидком состоянии, Mi – молярная масса компонента i в сплаве); VE – избыточный молярный объем при образовании сплава, которым для упрощения пренебрегаем; α = 0,155 ± 0,015 – параметр, полученный из отношения энергии активации вязкого течения чистых жидких металлов к их энергии когезии при температуре плавления; \(\Delta G_i^*\) – свободная энергия активации вязкого течения чистого компонента i в жидком состоянии, которая рассчитывается по измеренной вязкости чистого компонента i при определенной температуре по следующей формуле:
\[\Delta G_i^* = RT\ln \left( {\frac{{{\eta _i}{V_i}}}{{h{N_A}}}} \right).\]
Результаты работы и их обсуждение
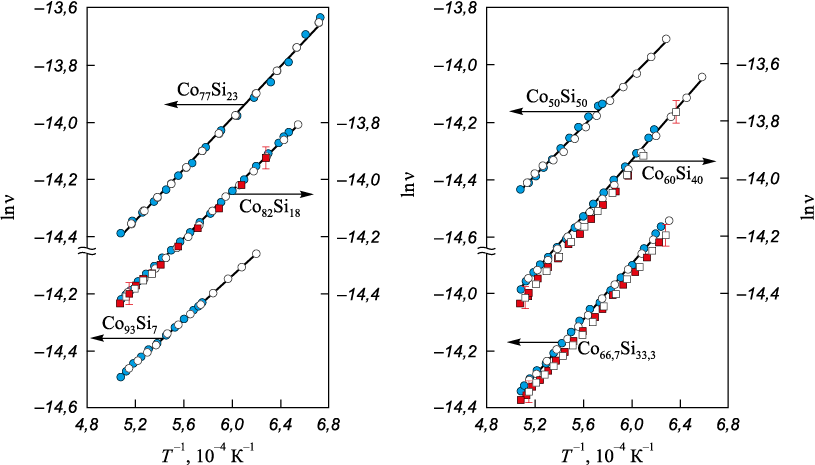
Проведены исследования кинематической вязкости расплавов систем Co – B (37 составов) и Co – Si (24 состава) в интервале от 0 до 54 ат. % металлоида. Типичные температурные зависимости вязкости представлены на рис. 1, 2. Политермы вязкости не имеют каких-либо особенностей и хорошо аппроксимируются уравнением Аррениуса:
| \[\nu = A\exp \left( {\frac{{{E_a}}}{{RT}}} \right),\] | (3) |
где А – постоянная; Еа – энергия активации вязкого течения. При повторных экспериментах полученные данные воспроизводятся в пределах погрешности измерения (рис. 2). Отсутствие различий в значениях вязкости, полученных в режиме нагрева и охлаждения, а также линейная зависимость логарифма вязкости от обратной абсолютной температуры в переохлажденной области свидетельствуют о сохранении структуры жидкого сплава в исследованном интервале температур.
Рис. 1. Политермы вязкости в координатах lnν – T –1 расплавов системы Co – B (ат. %)
Рис. 2. Политермы вязкости в координатах lnν – T –1 расплавов системы Co – Si (ат. %) |
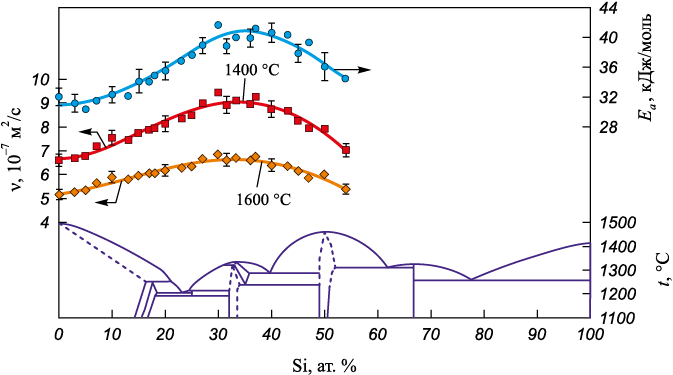
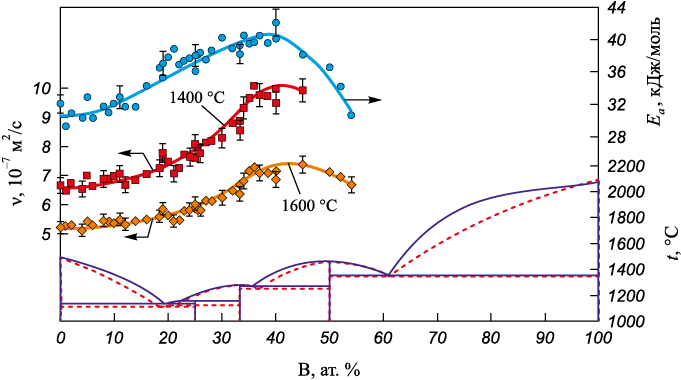
По полученным температурным зависимостям вязкости были рассчитаны концентрационные зависимости вязкости жидких сплавов систем Со – Si и Co – B (рис. 3, 4). Изотермы вязкости и энергии активации вязкого течения жидких сплавов кобальта с кремнием и бором имеют немонотонный куполообразный вид, что является косвенным подтверждением структурных изменений, происходящих в расплаве при изменении содержания металлоида. Наличие максимума на концентрационной зависимости вязкости обусловлено образованием атомных микрогруппировок из атомов разного сорта, упорядоченных предположительно по типу химических соединений [22].
Рис. 3. Концентрационные зависимости кинематической вязкости и энергии активации
Рис. 4. Концентрационные зависимости кинематической вязкости и энергии активации |
Поскольку максимум на изотерме вязкости системы Со – Si совпадает с существованием силицида Сo2Si на диаграмме состояния, то, вероятно, в расплавах при содержании 30 – 35 ат. % Si реализуется упорядочение по типу этого соединения. При содержании кремния менее 30 и более 35 ат. % расплавы имеют микронеоднородное строение, т. е. при содержании кремния менее 30 ат. % в расплаве, кроме микрогруппировок типа соединения Сo2Si, присутствуют области, состоящие преимущественно из атомов кобальта, а при содержании кремния более 35 ат. % – микрогруппировки с большим содержанием кремния, например, типа соединения СoSi.
Вязкость расплавов системы Co – B в области составов от 0 до 20 ат. % В мало изменяется с содержанием бора, что, по-видимому, связано с реализацией в расплаве ближнего упорядочения по типу твердого раствора. Рост значений ν и Еа при увеличении содержания бора в расплаве выше 20 ат. % также обусловлен образованием атомных микрогруппировок из атомов разного сорта, упорядоченных предположительно по типу химического соединения. Однако в данной системе корреляции между максимумом изотерм вязкости и стехиометрией соединений на диаграмме состояния не наблюдается.
Монотонный экспоненциальный характер политерм вязкости без гистерезиса, а также сохранение вида изотермы вязкости при нагреве указывают на отсутствие существенных изменений структуры расплавов при их нагреве. Можно полагать, что атомные микрогруппировки типа силицидов и боридов кобальта сохраняются в расплаве во всем исследованном интервале температур.
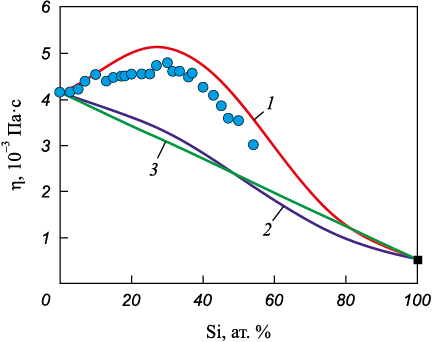
На рис. 5 приведены результаты расчетов концентрационной зависимости вязкости расплавов системы Co – Si. Необходимые данные по энтальпии смешения расплава и значение вязкости жидкого кремния взяты из работ [26; 27]. Из рис. 5 видно, что уравнение Козлова-Романова-Петрова прогнозирует не только близкие к экспериментальным данным значения вязкости, но и куполообразное поведение вязкости с концентрацией. Максимальное отклонение рассчитанных значений от экспериментальных составляет +11 %.
Рис. 5. Результаты расчета концентрационной зависимости |
Уравнение (2) было приведено к следующему виду:
| \[\ln \eta = {x_1}\ln {\eta _1} + {x_2}\ln {\eta _2} - \frac{{(0,155 \pm 0,015)\Delta H}}{{3RT}}.\] | (4) |
Для этого использовалось разложение lnVi = Vi – 1 и VE = 0. Пренебрежение избыточным молярным объемом при образовании сплава было реализовано в работе [8] при выводе уравнения Козлова-Романова-Петрова. Таким образом, уравнения Козлова-Романова-Петрова и Kaptay имеют схожий вид, различаясь лишь коэффициентом перед ΔH. При выводе уравнения (1) предполагалось, что в первом приближении основным движением атомов в металлическом расплаве остаются простые трехмерные колебания, поэтому коэффициент перед ΔH равен 1/3. В уравнении Kaptay коэффициент равен 1/6,5 и может быть получен, если учесть кроме трех колебательных степеней свободы еще и три вращательные степени для нелинейной молекулы. При выводе уравнения (2) предполагалось, что только малая доля энергии когезии (энтальпии) тратится во время вязкого течения, поэтому параметр α равен ΔZ/Z, где ΔZ – число разорванных связей во время вязкого течения, Z – среднее координационное число для расплава. Таким образом, ΔZ/Z = 1/3 согласно уравнению Козлова-Романова-Петрова, ΔZ/Z = 1/6,5 согласно уравнению Kaptay. Авторы работы [28] пришли к выводу, что при движении плотноупакованной жидкости (Z = 12) разрываются три связи, т. е. ΔZ/Z = 3/12 = 1/4. Полученный коэффициент близок к коэффициенту, который был получен в уравнении Козлова-Романова-Петрова и это уравнение наилучшим образом прогнозирует концентрационную зависимость вязкости расплавов системы Co – Si (рис. 5). Полученные результаты также согласуются с тем, что жидкий кобальт и расплавы Co – Si (до 40 ат. % Si), согласно дифракционным исследованиям [2], имеют плотную упаковку атомов.
При проведении расчета концентрационной зависимости вязкости расплавов системы Co – B возникли две проблемы, связанные с очень высокой температурой плавления (tm ~ 2075 °C) второго чистого компонента, т. е. бора, по отношению к температуре, при которой проводится расчет. Первая заключается в выборе значений динамической вязкости чистого бора (ηB ) и его плотности (ρB ), необходимой при вычислении молярного объема сплава. Возможно два варианта ее разрешения: первый вариант – ηB и ρB присвоить значения вязкости и плотности жидкого бора при его температуре плавления, т. е. ηB = (2,6 ± 0,3)·10–3 Па·с [29], ρB = 2170 ± 43 кг/м3 [30]; второй вариант – экстраполировать по уравнению (3) политерму вязкости [29] и линейным уравнением политерму плотности [30] жидкого бора до температуры 1627 °C, при которой рассчитывается изотерма бинарной системы (переохлажденный жидкий бор), тогда ηB = (10 ± 1)·10–3 Па·с и ρB = 2285 ± 46 кг/м3. Вторая проблема заключается в выборе концентрационной зависимости энтальпии смешения (ΔН) расплавов системы Co – B со стандартными состояниями «кристаллический бор – жидкий кобальт» [31], либо «жидкий переохлажденный бор – жидкий кобальт» [32].
Результаты варьирования значений динамической вязкости бора и энтальпии смешения на прогностические возможности уравнений представлены на рис. 6. Применение при вычислении изотерм вязкости для переохлажденного до 1627 °C жидкого бора приводит к неправильному ходу аддитивной зависимости вязкости системы Co – B (рис. 6, в, г). Поскольку расплавы Co – B характеризуются сильным взаимодействием между атомами разного сорта [33], в данной системе следует ожидать положительное отклонение изотермы вязкости от аддитивной зависимости, соответствующей идеальному раствору. Использование при расчете концентрационных зависимостей значения вязкости жидкого бора при его температуре плавления дает корректную аддитивную зависимость вязкости по отношению к изотерме, полученной в эксперименте (рис. 6, а, б). Такой подход может быть полезен и для других систем, в которых компоненты имеют существенные отличия в значениях температуры плавления.
Рис. 6. Результаты расчета концентрационной зависимости |
Из рис. 6 видно, что наиболее близкое совпадение рассчитанных изотерм вязкости с экспериментальной получено при использовании в расчетах значений вязкости жидкого бора при его температуре плавления и энтальпии смешения со стандартным состоянием «кристаллический бор – жидкий кобальт» (рис. 6, а). При этом уравнение Kaptay дает хорошее согласие с экспериментом до 20 ат. % B, а уравнение Козлова-Романова-Петрова в области от 40 до 54 ат. %. Отклонение от эксперимента прогнозированных значений вязкости по уравнению Kaptay составляет –16 %, а по уравнению Козлова-Романова-Петрова +17 %.
Несмотря на все трудности в выборе значений параметров для расчета концентрационных зависимостей вязкости расплавов системы Co – B, уравнения Козлова-Романова-Петрова и Kaptay прогнозируют вполне реальные значения вязкости. Предлагается применять эти уравнения для прогнозирования изотерм вязкости жидкой системы, поскольку они имеют простой вид, а необходимые параметры можно найти в соответствующих справочниках.
Выводы
Проведены исследования методом крутильных колебаний кинематической вязкости жидкого кобальта и его бинарных расплавов с кремнием и бором в широких температурном (до 1700 °С) и концентрационном (от 0 до 54 ат. % металлоида) интервалах.
Температурные зависимости вязкости жидкого кобальта и его бинарных расплавов с кремнием и бором с содержанием металлоида до 54 ат. %, полученные в режиме нагрева и охлаждения, совпадают (гистерезис отсутствует), имеют монотонный характер и хорошо описываются уравнением Аррениуса. Экспоненциальный характер поведения политерм вязкости указывает на сохранение структуры жидких сплавов как в жидком, так и в переохлажденном состояниях.
Концентрационные зависимости вязкости и энергии активации вязкого течения расплавов системы Co – Si и Co – B имеют сложный немонотонный куполообразный вид с максимальными значениями при 35 ат. % Si и 40 ат. % В. Немонотонный характер изотерм указывает на структурные изменения, происходящие в расплаве при изменении его состава.
Впервые проведены расчеты концентрационных зависимостей вязкости высокотемпературных расплавов систем типа металл –металлоид по уравнениям с термодинамическими величинами. Установлено, что концентрационную зависимость вязкости расплавов систем Co – Si и Co – B наилучшим способом прогнозирует уравнение Козлова-Романова-Петрова с максимальным отклонением от экспериментальных данных на 11 и 17 % соответственно. Предложен способ применения таких уравнений для прогнозирования изотерм вязкости жидкой системы, компоненты которой обладают существенно различными температурами плавления.
Список литературы
1. Gruner S., Marczinke J., Hennet L., Hoyer W., Cuello G.J. On the atomic structure of liquid Ni–Si alloys: A neutron diffraction study. Journal of Physics: Condensed Matter. 2009;21(38):385403. http://doi.org/10.1088/0953-8984/21/38/385403
2. Роик А.С., Сокольский В.Э., Казимиров В.П. Рентгенодифракционное исследование структуры расплавов системы Co-Si. Расплавы. 2003;(6):69–69.
3. Wang H.P., Wei B. Thermophysical property of undercooled liquid binary alloy composed of metallic and semiconductor elements. Journal of Physics D: Applied Physics. 2008;42(3):035414. http://doi.org/10.1088/0022-3727/42/3/035414
4. Sun H., Zhang C., Tang L., Wang R., Xia W., Wang C.Z. Molecular dynamics simulation of Fe-Si alloys using a neural network machine learning potential. Physical Review B. 2023;107(22):224301. https://doi.org/10.1103/PhysRevB.107.224301
5. Ravi K.R., Pillai R.M., Amaranathan K.R., Pai B.C., Chakraborty M. Fluidity of aluminum alloys and composites: A review. Journal of Alloys and Compounds. 2008;456(1-2): 201–210. https://doi.org/10.1016/j.jallcom.2007.02.038
6. Parthiban R., Stoica M., Kaban I., Kumar R., Eckert J. Viscosity and fragility of the supercooled liquids and melts from the Fe–Co–B–Si–Nb and Fe–Mo–P–C–B–Si glass-forming alloy systems. Intermetallics. 2015;66:48–55. https://doi.org/10.1016/j.intermet.2015.06.016
7. Shi R., Luo A.A. Applications of CALPHAD modeling and databases in advanced lightweight metallic materials. Calphad. 2018;62:1–17. https://doi.org/10.1016/j.calphad.2018.04.009
8. Козлов Л.Я., Романов Л.М., Петров Н.Н. Прогнозирование вязкости многокомпонентных металлических расплавов. Известия вузов. Черная металлургия. 1983;26(3):7–11.
9. Kaptay G. A new equation to estimate the concentration dependence of the viscosity of liquid metallic alloys from the heat of mixing data. In: Proceedings of microCAD 2003 conference, Section C: Metallurgy, March 6–7, 2003, Miskolc. Miskolc: University of Miskolc; 2003:23–28.
10. Gąsior W. Viscosity modeling of binary alloys: Comparative studies. Calphad. 2014;44:119–128. https://doi.org/10.1016/j.calphad.2013.10.007
11. Бельтюков А.Л., Ладьянов В.И. Автоматизированная установка для определения кинематической вязкости металлических расплавов. Приборы и техника эксперимента. 2008;(20):155–161.
12. Швидковский Е.Г. Некоторые вопросы вязкости расплавленных металлов. Москва: Гостехиздат; 1955:208.
13. Олянина Н.В., Бельтюков А.Л., Гончаров О.Ю., Ладьянов В.И. Влияние поверхностной пленки на результаты измерения вязкости расплава Co83B17 методом крутильных колебаний. Расплавы. 2012;(2):83–90.
14. Beltyukov A., Olyanina N., Ladyanov V. The viscosity of liquid Co-Si-B alloys. Journal of Molecular Liquids. 2019;281:204–215. https://doi.org/10.1016/j.molliq.2019.02.064
15. Бельтюков А.Л., Ладьянов В.И., Олянина Н.В. Об особенностях измерения вязкости металлических расплавов методом крутильных колебаний. Расплавы. 2009;(6): 19–27.
16. Олянина Н.В., Бельтюков А.Л., Ладьянов В.И. О вязкости жидких сплавов кобальта с бором и кремнием. Химическая физика и мезоскопия. 2019;21(1):55–64. https://doi.org/10.15350/17270529.2019.1.8
17. Бельтюков А.Л., Олянина Н.В., Ладьянов В.И. Особенности измерения вязкости металлических расплавов методом крутильных колебаний. Расплавы. 2016;(2):176–184.
18. Штернер С.Р., Довгопол С.П. Плотность, электросопротивление и ближний порядок расплавов Co-B и Ni-B. Украинский физический журнал. 1983;28(6):858–861.
19. Тавадзе Ф.Н., Байрамашвили И.А., Хантадзе Д.В. Поверхностное натяжение и строение расплавленных боридов железа, кобальта и никеля. ДАН СССР. 1965;162(1):67–69.
20. Гельд П.В., Гертман Ю.М. Плотности жидких сплавов кремния с кобальтом и никелем. Физика металлов и металловедение. 1961;12(1):47–50.
21. Глесстон С., Лейдлер К., Эйринг Г. Теория абсолютных скоростей реакций: кинетика химических реакций, вязкость, диффузия и электрохимические явления. Пер. с англ. Москва: Иностранная литература; 1948:583.
22. Вилсон Д.Р. Структура жидких металлов и сплавов. Пер. с англ. Москва: Металлургия; 1972:247.
23. Ishida K., Nishizawa T., Schlesinger M.E. The Co-Si (cobalt-silicon) system. Journal of Phase Equilibria. 1991;12(5): 578–586. https://doi.org/10.1007/BF02645074
24. Du Y., Schuster J., Chang Y.A., Jin Z., Huang B.Y. A thermodynamic description of the B-Co system: Modeling and experiment. International Journal of Materials Research. 2002;93(11):1157–1163. https://doi.org/10.1515/ijmr-2002-0198
25. Liao P.K., Spear K.E. The B-Co (boron-cobalt) system. Bulletin of Alloy Phase Diagrams. 1988;9(4):452–457. https://doi.org/10.1007/BF02881866
26. Chart T.G. Thermochemical data for transition metal-silicon systems. High Temperatures-High Pressures. 1973;5(3): 241–252.
27. Sato Y., Kameda Y., Nagasawa T., Sakamoto T., Moriguchi S., Yamamura T., Waseda Y. Viscosity of molten silicon and the factors affecting measurement. Journal of Crystal Growth. 2003;249(3–4):404–415. https://doi.org/10.1016/S0022-0248(02)02153-X
28. Takahira N. Influence of enthalpy changes on the temperature dependency of the viscosity of pure liquid metals. ISIJ International. 2015;55(10):2247–2251. https://doi.org/10.2355/isijinternational.ISIJINT-2015-214
29. Okada J.T., Ishikawa T., Watanabe Yu., Paradis P.F., Watanabe Ya., Kimura K. Viscosity of liquid boron. Physical Review B. 2010;81(14):140201(R). https://doi.org/10.1103/PhysRevB.81.140201
30. Paradis P.F., Ishikawa T., Yoda S. Noncontact density measurements of liquid, undercooled, and high temperature solid boron. Applied Physics Letters. 2005;86(15):151901. https://doi.org/10.1063/1.1900954
31. Franke P., Neuschütz D. B-Co (boron-cobalt). In: Thermodynamic Properties of Inorganic Materials. Binary systems. Part 2: Elements and Binary Systems from B-C to Cr-Zr. Berlin: Springer Materials; 2004;19B2:1-3. https://doi.org/10.1007/10757405_3
32. Witusiewicz V.T. Thermodynamic properties of liquid alloys of 3d transition metals with metalloids (silicon, carbon and boron). Journal of Alloys and Compounds. 1994;203: 103–116. https://doi.org/10.1016/0925-8388(94)90720-X
33. Мудрый С.И. Структура расплавов системы Co-B. Неорганические материалы. 1998;34(1):43–44.
Об авторах
Н. В. ОлянинаРоссия
Наталья Владимировна Олянина, к.ф.-м.н., научный сотрудник
Россия, 426067, Удмуртская Республика, Ижевск, ул. им. Татьяны Барамзиной, 34
А. Л. Бельтюков
Россия
Анатолий Леонидович Бельтюков, к.ф.-м.н., ведущий научный сотрудник
Россия, 426067, Удмуртская Республика, Ижевск, ул. им. Татьяны Барамзиной, 34
В. И. Ладьянов
Россия
Владимир Иванович Ладьянов, д.ф.-м.н., главный научный сотрудник, руководитель научного центра металлургической физики и материаловедения
Россия, 426067, Удмуртская Республика, Ижевск, ул. им. Татьяны Барамзиной, 34
Рецензия
Для цитирования:
Олянина Н.В., Бельтюков А.Л., Ладьянов В.И. Вязкость жидких сплавов кобальта с кремнием и бором: эксперимент и расчет. Известия высших учебных заведений. Черная Металлургия. 2025;68(5):517-525. https://doi.org/10.17073/0368-0797-2025-5-517-525
For citation:
Olyanina N.V., Beltyukov A.L., Ladyanov V.I. Viscosity of liquid alloys of cobalt with silicon and boron: Experiment and calculation. Izvestiya. Ferrous Metallurgy. 2025;68(5):517-525. https://doi.org/10.17073/0368-0797-2025-5-517-525
JATS XML