Scroll to:
Viscosity of liquid alloys of cobalt with silicon and boron: Experiment and calculation
https://doi.org/10.17073/0368-0797-2025-5-517-525
Abstract
The temperature (up to 1700 °C) and concentration dependences of the viscosity of liquid binary alloys of cobalt with silicon and boron were studied using an oscillating-cup method. The viscosity polytherms of liquid cobalt and its melts with silicon and boron (up to 54 at. % of the metalloid) are monotonous character without any anomalies and are well described by the Arrhenius equation. Coincidence of the viscosity polytherms obtained in the heating and cooling modes and linear dependence of the viscosity logarithm on the inverse absolute temperature in the supercooled region indicate the preservation of the liquid alloy structure. Microheterogeneous structure of Co – Si and Co – B melts (up to 54 at. % metalloid), associated with the formation of microgroups based on silicides and borides of cobalt with stronger internal bonds, leads to a complex form of concentration dependences of their viscosity and activation energy of viscous flow. The prognostic capabilities of the Kozlov-Romanov-Petrov and Kaptay equations for describing the concentration dependences of the viscosity of liquid metal-metalloid alloys are discussed. Features associated with the application of these equations to the systems in which one of the alloy components (in this case, boron in the Co – B system) is in the solid state at the calculation temperatures are considered. It is shown that the correct way to solve the problem is to use the viscosity value of liquid boron at its melting point as an input parameter for calculating the viscosity isotherms of the Co – B melts. The Kozlov-Romanov-Petrov and Kaptay equations differ only in the coefficients before the melt mixing enthalpy, the physical meaning of which is discussed in the paper. The Kozlov-Romanov-Petrov equation can be recommended for predicting the concentration dependences of the viscosity of liquid alloys of cobalt with silicon and boron.
Keywords
For citations:
Olyanina N.V., Beltyukov A.L., Ladyanov V.I. Viscosity of liquid alloys of cobalt with silicon and boron: Experiment and calculation. Izvestiya. Ferrous Metallurgy. 2025;68(5):517-525. https://doi.org/10.17073/0368-0797-2025-5-517-525
Introduction
Viscosity is an important physical property of a liquid, governed by interparticle interactions and linked to its structure. It is therefore widely used to probe the structure of high-temperature metallic melts. This is especially relevant for metal-metalloid systems, for which direct diffraction studies have been performed only for individual alloys [1] or at small superheatings above the liquidus line [2]; moreover, the coexistence of metallic and covalent bonding makes the use of modeling methods for these systems a persistent challenge [3; 4].
Accurate viscosity values are needed for many metallurgical processes involving the liquid state [5 – 7]. To predict the viscosity of multicomponent liquid alloys, thermodynamic-based equations are used, in particular the Kozlov–Romanov–Petrov equation [8] and the Kaptay equation [9]. The required input data for these equations are the viscosities of the pure liquid components that form the melt and the melt mixing enthalpy. According to [10], these equations predict the concentration dependences of viscosity well across systems with different phase diagrams. However, validation has mostly been carried out for metal–metal systems. Many advanced materials, by contrast, contain metalloids as well as high-melting elements such as boron, tantalum, and niobium. The presence of refractory elements complicates the application of these equations, because calculations are performed at temperatures at which these elements are in the solid state.
In the present work, experimental measurements of the viscosity of liquid alloys in the Co – Si and Co – B systems are reported, and the applicability of the Kozlov–Romanov–Petrov and Kaptay equations for predicting their concentration dependence is analyzed.
Materials and methods
Co – Si and Co – B master alloys (54 at. % metalloid) were produced in a vacuum resistance furnace by alloying cobalt powder grade PK-1u per GOST 9721–79 (cobalt content ≥99.35 wt. %; principal impurities, wt. %: <0.2 Fe; 0.4 Ni; 0.02 Si and C; 0.04 Cu) with single-crystal silicon (99.9999 wt. % Si) or amorphous boron per TU 113–12–132–83 (94 wt. % B; principal impurities, wt. %: 0.23 Fe; 0.1 Si) in a corundum crucible at a pressure of 10–2 Pa, a temperature of 1550 °C, and a 20-min hold. Samples of the required composition were then obtained by alloying cobalt grade K0 per GOST 123–2008 (cobalt content ≥99.98 wt. %; principal impurities, wt. %: <0.003 Fe; <0.005 Ni and C; up to 0.001 Si, Cu, Mg, Zn, and Al) with the Co – Si or Co – B master alloys in the viscometer furnace immediately prior to viscosity measurements.
The kinematic viscosity (ν) of the liquid alloys was measured on an automated setup [11] using the oscillating-cup method in the Shvidkovsky modification [12]. Experiments were carried out in a protective helium atmosphere (grade A) after evacuating the chamber to a pressure of 10–2 Pa. Viscosity was measured on heating and subsequent cooling, with stepwise temperature increments of 20 – 30 °C following 10-min isothermal holds at each temperature step. Measurements were carried out in cylindrical Al2O3 crucibles with two opposing end-face friction surfaces (the crucible bottom and a lid resting on the melt surface). To create the second end-face surface, a lid with an outer diameter 0.5 – 0.8 mm smaller than the crucible’s inner diameter was placed on the sample. The lid design [13; 14] allows free translation along the crucible’s vertical axis and co-oscillation with the crucible during torsional oscillations of the suspension system. Using two end-face friction surfaces helps account for uncertainties in viscosity calculations arising from potential oxide-film formation on the melt surface [13; 15] and from wetting of the crucible walls by the liquid metal (meniscus effects) [16; 17]. Prior to viscosity measurements, the samples were remelted at 1680 °C for 10 min to eliminate irreversible processes associated with alloying of the initial charge materials. The total error of viscosity determination at the 0.95 confidence level does not exceed 4 %, with a single-measurement error of 1.5 %; error analysis followed the procedure in [11].
Dynamic viscosity (η) was obtained using literature density data [18 – 20].
Equations for calculating viscosity
The Kozlov–Romanov–Petrov equation [8] was derived within the framework of the theory of oscillatory liquids by relating atomic vibrational motions to the free energy of the solution using the Einstein approximation, and has the following form:
| \[\ln \eta = {x_1}\ln {\eta _1} + {x_2}\ln {\eta _2} - \frac{{\Delta H}}{{3RT}},\] | (1) |
where η and ηi are the dynamic viscosity of the melt and of its pure components (i = 1, 2), respectively; xi is the mole fraction of component i in the alloy; ΔH is the integral mixing enthalpy of the melt; R is the universal gas constant; T is the absolute temperature.
The Kaptay equation [9] is a modification of Eyring’s equation [21] for multicomponent alloys and has the following form:
| \[\eta = \frac{{h{N_A}}}{{\sum\limits_{i = 1}^2 {\left( {{x_i}{V_i}} \right)} + {V^E}}}\exp \left( {\frac{{\sum\limits_{i = 1}^2 {\left( {{x_i}\Delta G_i^*} \right)} - \alpha \Delta H}}{{RT}}} \right),\] | (2) |
where Vi is the molar volume of pure component i in the liquid state (Vi = Mi /ρi , where ρi is the density of pure component i in the liquid state, Mi is the molar mass of component i in the alloy); V E is the excess molar volume upon alloy formation, which is neglected for simplicity; α = 0.155 ± 0.015 is a parameter obtained from the ratio of the activation energy of viscous flow of pure liquid metals to their cohesive energy at the melting temperature; \(\Delta G_i^*\) is the free energy of activation of viscous flow of pure component i in the liquid state, which is calculated from the measured viscosity of the pure component at a given temperature by the following expression:
\[\Delta G_i^* = RT\ln \left( {\frac{{{\eta _i}{V_i}}}{{h{N_A}}}} \right).\]
Results and discussion
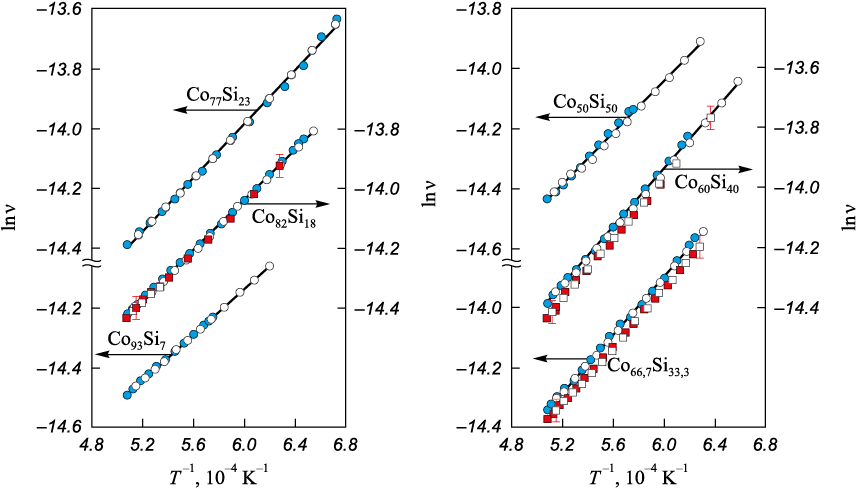
The kinematic viscosity of melts in the Co – B (37 compositions) and Co – Si (24 compositions) systems was investigated over the range from 0 to 54 at. % metalloid. Typical viscosity polytherms are shown in Figs. 1 and 2. The viscosity polytherms exhibit no anomalies and are well approximated by the Arrhenius equation:
| \[\nu = A\exp \left( {\frac{{{E_a}}}{{RT}}} \right),\] | (3) |
where А is a constant; Еа is the activation energy of viscous flow. In repeated experiments, the measured data are reproduced within the measurement error (Fig. 2). The absence of differences between viscosities obtained on heating and on cooling, together with the linear dependence of lnν on the inverse absolute temperature in the supercooled region, indicates preservation of the liquid alloy structure over the temperature range studied.
Fig. 1. Viscosity polytherms in lnν – T –1 coordinates of the Co – B (at. %) melts in heating (
Fig. 2. Viscosity polytherms in lnν – T –1 coordinates of the Co – Si (at. %) melts |
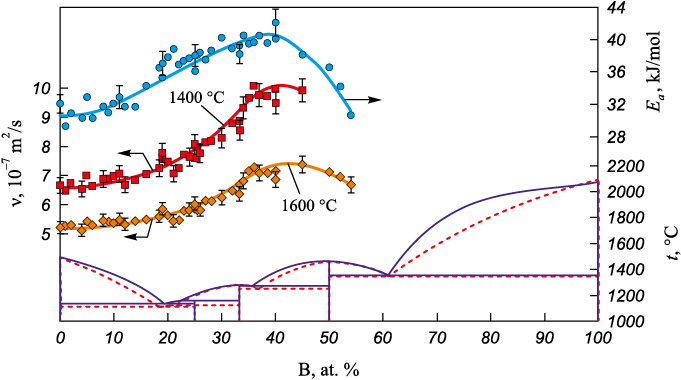
Based on the obtained viscosity polytherms, the concentration dependences for the liquid alloys of the Co – Si and Co – B systems were calculated (Figs. 3, 4). The isotherms of viscosity and of the activation energy of viscous flow for cobalt – silicon and cobalt – boron melts are nonmonotonic and dome-shaped, providing indirect evidence of structural rearrangements in the melt as the metalloid content varies. The maximum in the viscosity–composition curve is attributed to the formation of atomic microgroups composed of unlike atoms, presumably ordered in the manner of intermetallic compounds [22].
Fig. 3. Concentration dependences of kinematic viscosity and activation energy of viscous
Fig. 4. Concentration dependences of a kinematic viscosity and activation energy |
Because the maximum on the viscosity isotherm of the Co – Si system coincides with the presence of Co2Si on the phase diagram, melts containing 30 – 35 at. % Si are likely to exhibit Co2Si-type ordering. At silicon contents below 30 at. % and above 35 at. %, the melts are microheterogeneous: below 30 at. % Si they contain, in addition to Co2Si-type microgroups, regions dominated by cobalt atoms, whereas above 35 at. % Si they contain silicon-richer microgroups, for example of the CoSi type.
In the Co – B system, the viscosity changes little over 0 – 20 at. % B, which likely reflects short-range order consistent with a solid-solution–like arrangement in the melt. At boron contents above 20 at. %, both ν and Еа increase, attributable to the formation of atomic microgroups of unlike atoms, presumably ordered in the manner of a compound. However, in this system no correlation is observed between the maxima of the viscosity isotherms and the stoichiometries of compounds on the phase diagram.
The monotonic, exponential character of the viscosity polytherms without hysteresis, together with retention of the viscosity-isotherm shape on heating, indicates that no substantial structural changes occur during heating. This suggests that microgroups of cobalt silicides and borides persist throughout the temperature range investigated.
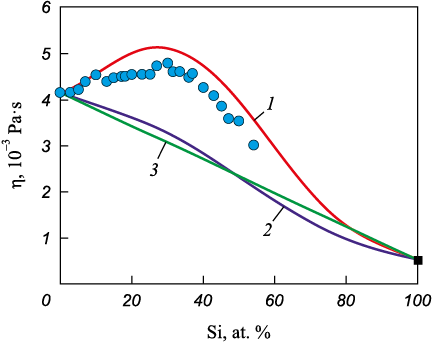
Fig. 5 presents the results of calculating the concentration dependence of viscosity for Co – Si melts. The required data on the mixing enthalpy of the melt and the viscosity of liquid silicon were taken from [26; 27]. As seen in Fig. 5, the Kozlov–Romanov–Petrov equation predicts not only viscosity values close to the experimental data but also the observed dome-shaped concentration behavior. The maximum deviation of the calculated from the experimental values is +11 %.
Fig. 5. Calculation results for concentration dependence of dynamic viscosity (η) |
Equation (2) was recast into the following form by using the expansion lnVi = Vi – 1 and setting VE = 0:
| \[\ln \eta = {x_1}\ln {\eta _1} + {x_2}\ln {\eta _2} - \frac{{(0.155 \pm 0.015)\Delta H}}{{3RT}}.\] | (4) |
Neglect of the excess molar volume upon alloy formation was also employed in [8] when deriving the Kozlov–Romanov–Petrov equation. Thus, the Kozlov–Romanov–Petrov and Kaptay equations have similar forms and differ only in the coefficient before ΔH. In deriving Equation (1), it was assumed, to first approximation, that atomic motion in a metallic melt is dominated by simple three-dimensional vibrations; hence the coefficient in front of ΔH equals 1/3. In the Kaptay equation the coefficient is 1/6.5, which follows if, in addition to three vibrational degrees of freedom, three rotational degrees of freedom of a nonlinear molecule are considered. In the derivation of Equation (2), only a small fraction of the cohesive energy (enthalpy) was assumed to be expended during viscous flow; therefore, α = ΔZ/Z, where ΔZ is the number of broken bonds during viscous flow and Z is the average coordination number of the melt. Accordingly, ΔZ/Z = 1/3 for the Kozlov–Romanov–Petrov model and ΔZ/Z = 1/6.5 for the Kaptay model. Reference [28] concluded that in a close-packed liquid (Z = 12) three bonds are broken during flow, i.e., ΔZ/Z = 3/12 = 1/4. This coefficient is close to that implied by the Kozlov–Romanov–Petrov equation, which indeed provides the best prediction of the concentration dependence of viscosity for Co – Si melts (Fig. 5). These findings are also consistent with diffraction data [2] indicating that liquid cobalt and Co – Si melts (up to 40 at. % Si) possess a close-packed atomic structure.
When calculating the concentration dependence of viscosity for the Co – B system, two issues arise due to the very high melting temperature (tm ≈ 2075 °C) of the second pure component, boron, relative to the calculation temperature. The first concerns the choice of the dynamic viscosity (ηB ) and density (ρB ) of pure boron required to compute the molar volume of the melt. Two approaches are possible: assign to ηB and ρB the values for liquid boron at its melting point, namely ηB = (2.6 ± 0.3)·10–3 Pa·s [29] and ρB = 2170 ± 43 kg/m3 [30]; or extrapolate the viscosity polytherm of liquid boron using Equation (3) [29] and extrapolate the density polytherm linearly [30] to 1627 °C, the temperature at which the binary isotherm is calculated (supercooled liquid boron), yielding ηB = (10 ± 1)·10–3 Pa·s and ρB = 2285 ± 46 kg/m3. The second issue is the choice of the concentration dependence of the mixing enthalpy (ΔН) for Co – B melts with the standard states taken as either “crystalline boron – liquid cobalt” [31] or “liquid supercooled boron – liquid cobalt” [32].
The effects of varying the dynamic viscosity of boron and the mixing enthalpy on the predictive capability of the equations are shown in Fig. 6. Using properties of supercooled liquid boron at 1627 °C in the viscosity-isotherm calculations yields an incorrect additive (ideal solution) trend for the viscosity of the Co – B system (Fig. 6, c, d). Because Co – B melts exhibit strong unlike-atom interactions [33], a positive deviation of the viscosity isotherm from the additive dependence expected for an ideal solution is anticipated. In contrast, using the viscosity of liquid boron at its melting point as an input yields an additive trend consistent with the experimentally determined isotherm (Fig. 6, a, b). This approach should also be useful for systems whose components have markedly different melting temperatures.
Fig. 6. Calculation results for concentration dependence |
As seen in Fig. 6, the closest agreement between calculated and experimental viscosity isotherms is obtained when the viscosity of liquid boron at its melting point is combined with the mixing enthalpy referenced to the standard states “crystalline boron – liquid cobalt” [31] (Fig. 6, a). Under these conditions, the Kaptay equation reproduces the data up to 20 at. % B, whereas the Kozlov–Romanov–Petrov equation performs better in the 40 – 54 at. % B range. The deviations from experiment are –16 % for the Kaptay equation and +17 % for the Kozlov–Romanov–Petrov equation.
Despite the difficulties in choosing parameter values for calculating the concentration dependences of viscosity in the Co – B system, both the Kozlov–Romanov–Petrov and Kaptay equations predict physically reasonable viscosity values. Given their simple form and the availability of the required parameters in standard data sources, these equations are recommended for predicting viscosity isotherms of liquid systems.
Conclusions
The kinematic viscosity of liquid cobalt and its binary melts with silicon and boron was measured by the oscillating-cup method over wide temperature (up to 1700 °C) and composition (0 – 54 at. % metalloid) ranges.
The resulting viscosity polytherms, obtained on heating and on cooling, coincide (no hysteresis), are monotonic, and are well described by the Arrhenius equation. Their exponential character indicates preservation of the liquid alloy structure in both liquid and supercooled states.
The concentration dependences of viscosity and of the activation energy of viscous flow for Co – Si and Co – B melts are nonmonotonic and dome-shaped, with maxima at 35 at. % Si and 40 at. % B, respectively – signatures of composition-driven structural changes in the melt.
For the first time, concentration dependences of viscosity of high-temperature metal–metalloid melts were calculated using thermodynamic-based equations. The Kozlov–Romanov–Petrov equation provides the best overall prediction for the Co – Si and Co – B systems, with maximum deviations from experiment of 11 and 17 %, respectively. A practical procedure is proposed for predicting viscosity isotherms in liquid systems whose components have substantially different melting temperatures.
References
1. Gruner S., Marczinke J., Hennet L., Hoyer W., Cuello G.J. On the atomic structure of liquid Ni–Si alloys: A neutron diffraction study. Journal of Physics: Condensed Matter. 2009;21(38):385403. http://doi.org/10.1088/0953-8984/21/38/385403
2. Roik A.S., Sokol’skii V.E., Kazimirov V.P. X-ray differaction investigation moltem Co-Si system. Rasplavy. 2003;(6): 69–69. (In Russ.).
3. Wang H.P., Wei B. Thermophysical property of undercooled liquid binary alloy composed of metallic and semiconductor elements. Journal of Physics D: Applied Physics. 2008;42(3):035414. http://doi.org/10.1088/0022-3727/42/3/035414
4. Sun H., Zhang C., Tang L., Wang R., Xia W., Wang C.Z. Molecular dynamics simulation of Fe-Si alloys using a neural network machine learning potential. Physical Review B. 2023;107(22):224301. https://doi.org/10.1103/PhysRevB.107.224301
5. Ravi K.R., Pillai R.M., Amaranathan K.R., Pai B.C., Chakraborty M. Fluidity of aluminum alloys and composites: A review. Journal of Alloys and Compounds. 2008;456(1-2): 201–210. https://doi.org/10.1016/j.jallcom.2007.02.038
6. Parthiban R., Stoica M., Kaban I., Kumar R., Eckert J. Viscosity and fragility of the supercooled liquids and melts from the Fe–Co–B–Si–Nb and Fe–Mo–P–C–B–Si glass-forming alloy systems. Intermetallics. 2015;66:48–55. https://doi.org/10.1016/j.intermet.2015.06.016
7. Shi R., Luo A.A. Applications of CALPHAD modeling and databases in advanced lightweight metallic materials. Calphad. 2018;62:1–17. https://doi.org/10.1016/j.calphad.2018.04.009
8. Kozlov L.Ya., Romanov L.M., Petrov N.N. Prediction of viscosity of multicomponent metallic melts. Izvestiya. Ferrous Metallurgy. 1983;26(3):7–11. (In Russ.).
9. Kaptay G. A new equation to estimate the concentration dependence of the viscosity of liquid metallic alloys from the heat of mixing data. In: Proceedings of microCAD 2003 conference, Section C: Metallurgy, March 6–7, 2003, Miskolc. Miskolc: University of Miskolc; 2003:23–28.
10. Gąsior W. Viscosity modeling of binary alloys: Comparative studies. Calphad. 2014;44:119–128. https://doi.org/10.1016/j.calphad.2013.10.007
11. Bel’tyukov A.L., Lad’yanov V.I. An automated setup for determining the kinematic viscosity of metal melts. Instruments and Experimental Techniques. 2008;51:304–310. https://doi.org/10.1134/S0020441208020279
12. Shvidkovsky E.G. Certain Problems of Molten Metals Viscosity. Moscow: Gostekhizdat; 1955:208. (In Russ.).
13. Olyanina N.V., Bel’tyukov A.L., Goncharov O.Yu., Lad’yanov V.I. Influence of surface film on results of measuring the viscosity of Co83B17 melt by method of torsional vibrations. Rasplavy. 2012;(2):83–90. (In Russ.).
14. Beltyukov A., Olyanina N., Ladyanov V. The viscosity of liquid Co-Si-B alloys. Journal of Molecular Liquids. 2019;281:204–215. https://doi.org/10.1016/j.molliq.2019.02.064
15. Bel’tyukov A.L., Lad’yanov V.I., Olyanina N.V. About of characteristic properties of measurement of stickiness metallic melts by method of torsional vibration. Rasplavy. 2009;(6):19–27. (In Russ.).
16. Olyanina N.V., Beltyukov A.L., Ladyanov V.I. Viscosity of liquid alloys of cobalt with boron and silicon. Chemical Physics and Mesoscopy. 2019;21(1):55–64. (In Russ.). https://doi.org/10.15350/17270529.2019.1.8
17. Bel’tyukov A.L., Olyanina N.V., Lad’yanov V.I. Torsional vibration measurement of the viscosity of a metallic melt. Russian Metallurgy (Metally). 2016;2016:156–161. https://doi.org/10.1134/S0036029516020026
18. Shterner S.R., Dovgopol S.P. Density, electric resistance and short-range order of Co-B and Ni-B melts. Ukrainskii fizicheskii zhurnal. 1983;28(6):858–861. (In Russ.).
19. Tavadze F.N., Bairamashvili I.A., Khantadze D.V. Surface tension and structure of molten borides of iron, cobalt and nickel. Soviet Physics Doklady. 1965;162(1):67–69. (In Russ.).
20. Geld P.V., Gertman Yu.M. Densities of liquid alloys of silicon with cobalt and nickel. Physics of Metals and Metallography. 1961;12(1):47–50. (In Russ.).
21. Glasstone S., Laidler K. L., Eyring H. The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena. New York; London: McGraw-Hill; 1941:611.
22. Wilson J.R. The structure of liquid metals and alloys. Metallurgical Reviews. 1965;10(1):381–590. http://dx.doi.org/10.1179/mtlr.1965.10.1.381
23. Ishida K., Nishizawa T., Schlesinger M.E. The Co-Si (cobalt-silicon) system. Journal of Phase Equilibria. 1991;12(5): 578–586. https://doi.org/10.1007/BF02645074
24. Du Y., Schuster J., Chang Y.A., Jin Z., Huang B.Y. A thermodynamic description of the B-Co system: Modeling and experiment. International Journal of Materials Research. 2002;93(11):1157–1163. https://doi.org/10.1515/ijmr-2002-0198
25. Liao P.K., Spear K.E. The B-Co (boron-cobalt) system. Bulletin of Alloy Phase Diagrams. 1988;9(4):452–457. https://doi.org/10.1007/BF02881866
26. Chart T.G. Thermochemical data for transition metal-silicon systems. High Temperatures-High Pressures. 1973;5(3): 241–252.
27. Sato Y., Kameda Y., Nagasawa T., Sakamoto T., Moriguchi S., Yamamura T., Waseda Y. Viscosity of molten silicon and the factors affecting measurement. Journal of Crystal Growth. 2003;249(3–4):404–415. https://doi.org/10.1016/S0022-0248(02)02153-X
28. Takahira N. Influence of enthalpy changes on the temperature dependency of the viscosity of pure liquid metals. ISIJ International. 2015;55(10):2247–2251. https://doi.org/10.2355/isijinternational.ISIJINT-2015-214
29. Okada J.T., Ishikawa T., Watanabe Yu., Paradis P.F., Watanabe Ya., Kimura K. Viscosity of liquid boron. Physical Review B. 2010;81(14):140201(R). https://doi.org/10.1103/PhysRevB.81.140201
30. Paradis P.F., Ishikawa T., Yoda S. Noncontact density measurements of liquid, undercooled, and high temperature solid boron. Applied Physics Letters. 2005;86(15):151901. https://doi.org/10.1063/1.1900954
31. Franke P., Neuschütz D. B-Co (boron-cobalt). In: Thermodynamic Properties of Inorganic Materials. Binary systems. Part 2: Elements and Binary Systems from B-C to Cr-Zr. Berlin: Springer Materials; 2004;19B2:1-3. https://doi.org/10.1007/10757405_3
32. Witusiewicz V.T. Thermodynamic properties of liquid alloys of 3d transition metals with metalloids (silicon, carbon and boron). Journal of Alloys and Compounds. 1994;203: 103–116. https://doi.org/10.1016/0925-8388(94)90720-X
33. Mudryi S.I. Structure of Co-B melts. Inorganic Materials. 1998;34(1):43–44. (In Russ.).
About the Authors
N. V. OlyaninaRussian Federation
Natalia V. Olyanina, Cand. Sci. (Phys.–Math.), Research Associate
34 Tatyana Baramzina Str., Izhevsk, Udmurtian Republic 426067, Russian Federation
A. L. Beltyukov
Russian Federation
Anatoly L. Beltyukov, Cand. Sci. (Phys.–Math.), Leading Researcher
34 Tatyana Baramzina Str., Izhevsk, Udmurtian Republic 426067, Russian Federation
V. I. Ladyanov
Russian Federation
Vladimir I. Ladyanov, Dr. Sci. (Phys.–Math.), Chief Researcher, Head of Scientific Center for Metallurgical Physics and Materials Science
34 Tatyana Baramzina Str., Izhevsk, Udmurtian Republic 426067, Russian Federation
Review
For citations:
Olyanina N.V., Beltyukov A.L., Ladyanov V.I. Viscosity of liquid alloys of cobalt with silicon and boron: Experiment and calculation. Izvestiya. Ferrous Metallurgy. 2025;68(5):517-525. https://doi.org/10.17073/0368-0797-2025-5-517-525