Перейти к:
Моделирование и оптимизация влияния температурных швов на напряженно-деформированное состояние сферических металлических литейных форм
https://doi.org/10.17073/0368-0797-2025-4-372-382
Аннотация
Задачей настоящего теоретического исследования является оценка влияния кольцевых температурных швов на внутренней поверхности литейной металлической сферической формы на уровень напряженно-деформированного состояния (НДС) в ней при кристаллизации стальной отливки. Специфика данного технологического процесса состоит в геометрической форме (сфера) литейной модели, когда кристаллизующийся металл создает во внутренней поверхности литейной формы (в первые мгновения) значительные сжимающие напряжения, которые усиливаются кривизной формы: внутренний слой формы, нагреваясь, пытается увеличиться в объеме, но этому препятствуют не только более холодные внешние слои, но и кривизна самого поверхностного слоя. Рассматриваются два варианта применения литейной формы: со швами и без них. Формулируется задача оптимизации конструктивных параметров температурных швов (выточек) от величины возникающих в литейной форме нормальных напряжений в начальной стадии кристаллизации стальной отливки. При решении задачи используются уравнения линейной теории упругости, уравнения теплопроводности и апробированный численный метод. Приведена численная схема и разработанный алгоритм решения задачи. Оценка трещиностойкости проводится по величине нормальных напряжений в металлической сферической форме. Найденные в результате решения тестовой задачи оптимальные конструктивные варианты (схемы) литейной сферической металлической формы зависят от расположения температурных швов в оболочковой форме, значений напряжений в них в условиях целевой функции min-max и разработанного алгоритма. Результаты решения задачи представлены графически в виде эпюр напряжений и температур по исследуемой области в разных сечениях и временах охлаждения ОФ и нарастающей корочки металла. Дан анализ полученных результатов стойкости металлической сферической литейной формы.
Ключевые слова
Для цитирования:
Евстигнеев А.И., Чернышова Д.В., Одиноков В.И., Дмитриев Э.А., Евстигнеева А.А., Колошенко Ю.Б., Потянихин Д.А. Моделирование и оптимизация влияния температурных швов на напряженно-деформированное состояние сферических металлических литейных форм. Известия высших учебных заведений. Черная Металлургия. 2025;68(4):372-382. https://doi.org/10.17073/0368-0797-2025-4-372-382
For citation:
Evstigneev A.I., Chernyshova D.V., Odinokov V.I., Dmitriev E.A., Evstigneeva A.A., Koloshenko Yu.B., Potyanikhin D.A. Modeling and optimization of the effect of temperature seams on stress-strain state of spherical metal casting molds. Izvestiya. Ferrous Metallurgy. 2025;68(4):372-382. https://doi.org/10.17073/0368-0797-2025-4-372-382
Введение
Металлические литейные формы широко применяются в литейном производстве в различных методах литья, например, при литье в кокиль, центробежном литье, литье под давлением, непрерывном литье, жидкой штамповке и др. Основным недостатком этих методов литья является малая долговечность работы металлических форм вследствие внешних силовых и температурных воздействий на них. Такие воздействия приводят к повышенному уровню напряженно-деформированного состояния (НДС) в формах, которые могут разрушаться, или к нарушению геометрии формы от возникающих температурных напряжений. Для снижения такого влияния в производстве применяют различные технологические и конструктивные решения.
Как показывает анализ литературных источников и производственный опыт, на стойкость литейных форм большое влияние оказывает геометрия получаемой в ней отливки. Наиболее непредсказуемой (с точки зрения стойкости литейной формы) является сферическая (шарообразная) форма отливки.
В действующем литейном производстве шарообразных отливок применяются различные типы литейных форм, а именно, разовые песчано-глинистые, керамические и разъемные металлические. Такие литейные формы подвергаются различным внешним силовым и температурным воздействиям, которые могут приводить к разрушению форм или сокращению их работоспособности.
Авторами работы [1] высказано теоретическое предположение и найдено принципиально новое технологическое решение1 по повышению стойкости сферической керамической оболочковой формы (ОФ) за счет выполнения на ее внутренней поверхности температурных швов. Идея такого технологического решения найдена в результате анализа известного в литейном производстве метода снижения термических напряжений в отливках за счет использования так называемых «ребер жесткости» [2], а в рассматриваемом случае – температурных швов (выточек). Температурный шов представляет собой кольцевую выточку на внутренней поверхности литейной ОФ.
Эволюция НДС металлической литейной формы при литье в кокиль рассматривается в работах [3; 4].
Расчет НДС кокилей осуществляется методом конечных элементов [3] в два этапа: решение задачи теплопроводности и решение задачи упруго-пластической деформации с использованием найденных температурных полей. Расчетные данные позволили спроектировать и внедрить в производство новые, более стойкие чугунные изложницы меньшей массы.
В работе [4] представлены данные по численному моделированию процессов формирования отливок в металлических формах. В качестве методической основы численного моделирования принят метод конечных разностей в варианте явной разностной схемы. Для реализации метода численного моделирования явлений теплопереноса в рассматриваемой системе тел использовалась прямоугольная пространственная сетка в пределах поддона. Шаги сетки в пределах формирующейся отливки, а также для стенки формы и слоя утеплителя сочетались с теплофизическими свойствами поддона для обеспечения условий гомохромности. Устойчивость расчета сохранялась благодаря принятому шагу по времени \(\bar \Delta \)τ ≤ 30 с, при котором число Фурье не превышает своего граничного значения. Задача решалась как двумерная.
Результаты моделирования НДС в затвердевающей стальной отливке [5; 6] позволили спрогнозировать образование в ней трещин, развитие которых зависит не только от температурных полей и связанных с ними тепловых напряжений и деформаций, но и от локализации усадочной пористости.
В работе [7] получено общее выражение, позволяющее рассчитать усадку и термические напряжения в упруго-пластическом диске, обусловленные круговым источником тепла, для произвольного нелинейного закона упрочнения, а также рассчитать упругую разгрузку упруго-пластического диска.
В работе [8] изучены упруго-пластические и остаточные напряжения в толстостенном сферическом сосуде под внешним гидростатическим давлением. В результате исследований был разработан процесс, позволяющий создавать благоприятные остаточные напряжения при сжатии во внутренней части цилиндрических и сферических сосудов.
Предметом работы [9] была функционально-градиентная полая сфера со сферической изотропией, подверженная внутреннему давлению. Целью работы являлась реализация благоприятного распределения напряжений в полой сфере, подверженной внутреннему давлению, для пластичного и хрупкого поведения материала.
В работе [10] рассмотрена переходная термоупругая задача, включающая многослойный полый цилиндр с кусочно-степенной неоднородностью из-за асимметричного нагрева с его поверхностей. Было исследовано влияние функциональной градации на термические напряжения.
Решалась численная задача в программном комплексе ANSYS Mechanical для двухслойной толстостенной сферической оболочки при температурно-силовом воздействии [11].
Решение задачи для напряжений и смещений в толстой сферической оболочке, подверженной внутренним и внешним нагрузкам давления, представлено в работе [12].
На основе теории плоской упругости определены компоненты смещения и напряжения в толстостенных сферических сосудах высокого давления, изготовленных из неоднородных материалов, подвергающихся внутреннему и внешнему давлению [13]. Исследуется влияние неоднородности материала на упругие деформации и напряжения.
Оптимизация конструкции для трехслойного цилиндра с термоусадкой из разных материалов, подвергающегося очень высокому давлению, исследовалась в работе [14].
В работе [15] проведено моделирование осесимметричной многослойной оболочки. Решена задача о плоской деформации для цилиндра, окруженного кольцевыми слоями. Показано численное решение для изучения зависимости распределения остаточных напряжений от свойств материала в процессе охлаждения.
В работе [16] исследовано влияние величины угла охвата поверхности сферической керамической ОФ опорным наполнителем (ОН) на уровень НДС в ней при получении стальной шарообразной отливки. Сформулирована задача по оптимизации стойкости сферической керамической ОФ от угла охвата ее ОН при затвердевании и охлаждении в ней стальной шарообразной отливки в условиях целевой функции min – max. Оценка трещиностойкости ОФ проводилась по величине нормальных напряжений в ней.
Для теоретического моделирования процесса эволюции НДС в форме на начальном этапе процесса охлаждения использованы уравнения линейной теории упругости, уравнения теплопроводности и апробированный численный метод [17], который широко применяется для решения других задач подобного рода.
Моделирование и оптимизация смежных вопросов в других различных процессах исследовались в работах [18; 19].
Целью работы [18] является создание эффективного численного алгоритма решения осесимметричных обратных задач проектирования средств тепловой маскировки (многослойных сферических маскировочных оболочек) и анализ результатов проведенных вычислительных экспериментов. В качестве процедуры численной оптимизации при решении данных задач применен оптимизационный метод роя частиц, предложенный в работе [20].
В работе [19] исследуется вопрос о пластической неустойчивости тонкостенного сферического сосуда из материала с пластической ортотропией, нагруженного внутренним импульсным давлением. С использованием программного обеспечения Mathematica установлено влияние скорости деформации и параметра пластической ортотропии на значение деформации, при котором возникает неустойчивость.
В настоящей работе анализируется стойкость сферической металлической литейной формы при кристаллизации в ней стальной отливки, а именно, развивается найденное ранее для керамических сферических ОФ технологическое решение уменьшения величины нормальных напряжений (по модулю) в сечении сферической ОФ путем упорядоченного расположения в ней выточек. Решается задача по нахождению оптимальной конструкции металлической формы сферической конфигурации, способной выдержать температурный перепад на начальном этапе процесса охлаждения при заливке в нее жидкой стали. Стойкость формы такой конфигурации имеет большое значение при изготовлении шарообразных отливок, применяемых в многочисленных конструкциях и имеющих высокие требования к точности изготовления.
Математическая постановка задачи
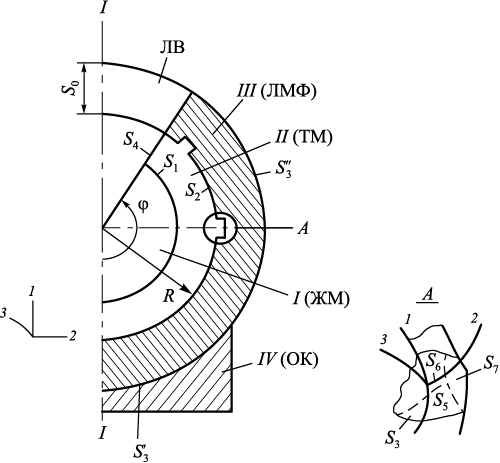
Рассматривается осесимметричное тело вращения (рис. 1), имеющее в меридианном сечении: I – жидкую фазу (сталь); II – твердую фазу (закристаллизовавшийся металл); III – литейную металлическую форму с кольцевыми выточками на внутренней поверхности; IV – опорную конструкцию (ОК). Форма разъемная с внутренними кольцевыми выточками. Жидкий металл заливается в полость литейной формы сверху через литниковую воронку (ЛВ). Вид А – эскиз круговой выточки во внутреннем слое формы с соответствующими поверхностями, по которым будут установлены граничные условия.
Рис. 1. Расчетная схема системы с указанием поверхности к граничным условиям задачи: |
Представленная ниже расчетная схема адекватно соответствует реальному технологическому процессу получения сферической стальной отливки в металлической форме.
Поскольку решается задача Коши, то физический фактор отвода тепла при охлаждении может быть осуществлен любым известным технологическим способом, например, естественным или принудительным охлаждением и т. п.
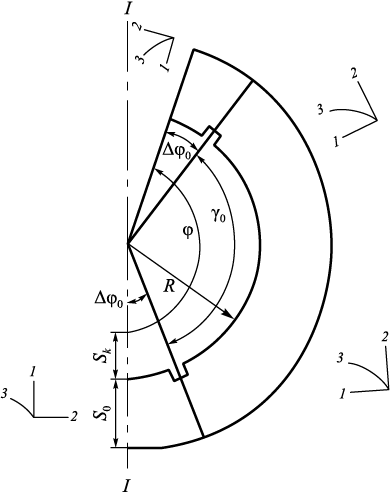
Рассмотрим вариант с двумя выточками на внутренней поверхности формы (рис. 2). Требуется найти такое рациональное их расположение на внутренней поверхности, чтобы наибольшие (по модулю) значения нормальных напряжений σ22 были бы минимальны.
Рис. 2. Схема системы I (ЖМ) – II (ТМ) – III (ЛМФ) к оптимизации конструкции |
Для этого условия целевая функция будет иметь вид:
| \[F = \min \left| {{\sigma _{22}}(\gamma )} \right|\max \left| {{\sigma _{22}}\left( {{{\left. Q \right|}_{{S_2}}},\tau } \right)} \right|\] | (1) |
при ограничениях
| \[\begin{array}{c}0 \le {\gamma _0} \le 120^\circ ;\\0 < \tau \le 15{\rm{ c}};\end{array}\] | (2) |
здесь Q – площадь меридианного сечения формы.
Ограничение по τ взято из решения подобной задачи, когда при охлаждении жидкого металла в форме без выточек напряжения σ22 , σ33 по сечениям уменьшаются по модулю уже при τ > 10 с. Ограничение по углу раствора γ0 следует из условия, что уменьшение сжимающих напряжений σ22 при наличии выточки распространяется на ограниченную область.
Центральную роль в задаче занимает решение системы уравнений линейной теории упругости на временном шаге \(\bar \Delta {\tau _n}\).
Используя уравнения линейной теории упругости, запишем для каждой из областей систему уравнений в декартовой системе координат:
‒ область I (жидкий металл):
| \[\begin{array}{c}{\sigma _{11}} = {\sigma _{22}} = {\sigma _{33}} = \sigma = - {P_1};\\\dot \theta = {a_1}\Delta \theta ;\end{array}\] | (3) |
‒ области II, III (закристаллизовавшийся твердый металл, форма):
| \[\left\{ \begin{array}{l}{\sigma _{ij,j}} = 0,{\rm{ }}i;\\{\sigma _{ij}} - \sigma {\delta _{ij}} = 2{G_p}\varepsilon _{ij}^*;{\rm{ }}\varepsilon _{ij}^* = {\varepsilon _{ij}} - \frac{1}{3}\varepsilon {\delta _{ij}};\\\varepsilon = {\varepsilon _{ii}};\\{\varepsilon _{ii}} = 3{k_p}\sigma + 3{\alpha _p}\left( {\theta - \theta _p^*} \right);\\{\varepsilon _{ij}} = 0,5\left( {{U_{i,j}} + {U_{j,i}}} \right);\\\dot \theta = {a_p}\Delta \theta ,\end{array} \right.\] | (4) |
где Ui – перемещения; εij – деформации; σ – гидростатическое напряжение; p = I, II, III – рассматриваемые области; Gp(θ) – модуль сдвига в области p (p = II, III); Gp (p = II, III) – модуль сдвига металла (p = II) и формы (p = III); δij – символ Кронекера; kp – коэффициенты объемного сжатия; αp – коэффициенты линейного расширения (p = II, III); ap – коэффициенты температуропроводности (p = I, II, III); θ – текущая температура; τ – время; \(\theta _p^*\) – начальные температуры в области p = I, II, III; P1 – давление в области I; \({a_p} = \frac{{{\lambda _p}}}{{{c_p}{\gamma _p}}};\) λp – коэффициент теплопроводности; cp – коэффициент теплоемкости; γp – удельный вес; Δ – оператор Лапласа.
В процессе охлаждения жидкого металла при условии, что θм ≤ θк (где θм – температура металла; θк – температура кристаллизации), определяется толщина затвердевшего слоя из решения межфазового перехода:
| \[\frac{{d{\theta _1}}}{{dn}}{\lambda _1} - \frac{{d{\theta _2}}}{{dn}}{\lambda _2} = \frac{{dx}}{{d\tau }}L\rho ;\] | (5) |
где θ1 и θ2 – температура твердой и жидкой фаз; λ1 и λ2 – коэффициент теплопроводности твердой и жидкой фазы; L – скрытая теплота плавления; ρ – плотность твердой фазы; x – текущая толщина корочки затвердевшего металла; n – нормаль к границе двух фаз.
Если предположить, что температура в твердой фазе по толщине δxn изменяется по линейному закону и градиент температуры в жидкой фазе равен нулю, то решение уравнения (5) дает следующую зависимость для определения толщины закристаллизовавшейся корочки δxn на временном шаге \(\bar \Delta {\tau _n}\) [21]:
| \[\delta {x_n} = C\sqrt \tau ;{\rm{ }}C = \sqrt {\frac{{2\bar \Delta {\theta _1}{\lambda _1}}}{{\rho L}}} ,\] | (6) |
здесь \(\bar \Delta {\theta _1}\) – перепад температур в твердой фазе вблизи фронта кристаллизации.
Начальные условия задачи (3), (4):
– \({\left. {\delta x} \right|_{\tau = 0}} = 0\) – отсутствие твердой фазы металла;
– \({\left. {{\theta _1}} \right|_{\tau = 0}} = {\theta _0}\) – температура разливаемого жидкого металла (1500 °С);
– \({\left. {\theta _3^*} \right|_{\tau = 0}} = {\theta ^*}\) – начальная температура формы (20 °С).
Начальные значения напряжений равны нулю.
Решение системы (3), (4) осуществляется в ортогональной системе координат. Задача осесимметричная:
U3 = 0; σ31 = σ32 = 0; ε31 = ε32 = 0.
Граничные условия задачи (3, 4) (рис. 1):
– на оси симметрии
U2 = 0; σ21 = 0; qп = 0;
– на поверхностях S1 – S8
| \[\begin{array}{c}{\left. {{\sigma _{11}}} \right|_{{S_1}}} = - {P_1};{\rm{ }}{\left. {{\sigma _{12}}} \right|_{{S_i}}} = 0{\rm{ }}(i = 1,{\rm{ }}5,{\rm{ }}6);\\{\left. {{\sigma _{11}}} \right|_{{{S''}_3}}} = 0;{\rm{ }}{\left. {{\sigma _{11}}} \right|_{{S_i}}} = 0{\rm{ }}(i = 5,{\rm{ }}6);\\{\left. {{\sigma _{12}}} \right|_{{S_3}}} = 0;{\rm{ }}{\left. {{\sigma _{22}}} \right|_{{S_i}}} = 0{\rm{ }}(i = 7,{\rm{ }}8);\\{\left. {{U_1}} \right|_{{{S'}_3}}} = 0;{\rm{ }}{\left. {{U_2}} \right|_{{S_4}}} = 0;{\rm{ }}{\left. {{\sigma _{21}}} \right|_{{S_i}}} = 0{\rm{ }}(i = 4,{\rm{ }}7,{\rm{ }}8);\\{\left. \theta \right|_{{S_1}}} = {\theta _0};{\rm{ }}{\left. \theta \right|_{{S_3}}} = {\theta ^*},\end{array}\] | (7) |
где qп – тепловой поток; \({S_3} = {S'_3} + {S''_3}\) – поверхности соприкосновения формы с опорной конструкцией и свободной поверхностью.
Для решения системы уравнений (3), (4) с граничными условиями (7) использован численный метод, описанный в работе [17] и примененный в исследованиях [21; 22] и др. Рассматриваемая область разбивается системой ортогональных поверхностей на элементы конечных размеров, для каждого элемента записывается система (3), (4) в разностной форме через значения напряжений и перемещений по граням элементов и длин дуг ребер, образующих элемент, которая решается с учетом начальных и граничных условий по разработанной в работе [17] методике и составленному алгоритму. Результаты решения: напряжения и перемещения по граням каждого элемента и средняя температура по каждому элементу на временном шаге. Численное решение задачи осуществлялось с использованием разработанной программы и программного комплекса «Одиссей»2.
Разностный аналог уравнения теплопроводности для ортогонального элемента строится из теплового баланса [17] и включает среднюю температуру по элементу и температуры окружающих его элементов, а также длины дуг, образующих ортогональные элементы. Численное решение этой системы уравнений осуществляется методом прогонки.
Алгоритм решения задачи
Решение задачи (1) с условиями (2) осуществляется согласно нижеописанному алгоритму.
1. Исследуемая область разбивается на конечное число ортогональных элементов; задаются геометрические размеры S и R.
2. Время охлаждения τ* = 15 с при решении задачи (1) с условиями (2) разбивается на конечное число шагов: τ* = \(\sum {\bar \Delta {\tau _n}} ,\) где n – номер временного шага.
3. Задаются физико-механические свойства материалов: жидкой и кристаллизующейся стали, формы.
4. Задаются геометрические размеры выточек \(\bar \Delta {\varphi _0}\), φ, γ0 .
5. Задается шаг по изменению текущего параметра γ: \(\bar \Delta \gamma \).
6. Задаются начальные и граничные условия по элементам, образующим рассматриваемую область, и областям, образующих выточки.
7. Вычисляются длины дуг элементов, образующих конкретную область.
8. Определяется поле температур на временном шаге \(\bar \Delta {\tau _n}\) численным решением уравнения теплопроводности при наличии начальных и граничных условий на данном временном шаге.
9. Если в области I у поверхности S2 температура \({\left. \theta \right|_{{S_2}}}\) ≤ θк , то вычисляется толщина закристаллизовавшейся корочки по формуле (6); следует перестройка сетки с операции 7. Если \({\left. \theta \right|_{{S_2}}}\) > θк , то выполняется операция 10.
10. Решается система уравнений (4) (исключая уравнения теплопроводности) по методике, описанной в работе [17]. Определяются поля напряжений σij и перемещений Ui (i, j = 1, 2, 3).
11. По области Q на поверхности S2 находится максимальное (по модулю) напряжение σ22 и заносится в матрицу \({\left\{ {{\sigma _2}} \right\}^\prime }\).
12. Производится шаг по времени. Если \(\sum {\bar \Delta {\tau _n}} \) < τ*, то выполняется операция 8. Если \(\sum {\bar \Delta {\tau _n}} \) = τ*, то выполняется операция 13.
13. Из матрицы \({\left\{ {{\sigma _2}} \right\}^\prime }\) находится значение σ22 = max\({\left\{ {{\sigma _2}} \right\}^\prime }\) и заносится в матрицу \({\left\{ {{\sigma _2}} \right\}^{\prime \prime }}\).
14. Производится шаг γn = γn – 1 – \(\bar \Delta \gamma \); τ = 0. Если γn = 0, то следует операция 15, если γn > 0, следует операция 6.
15. Из матрицы \({\left\{ {{\sigma _2}} \right\}^{\prime \prime }}\) выбирается значение \(\overline {{\sigma _{22}}} = \min {\left\{ {{\sigma _3}} \right\}^\prime }\) и соответствующие ему время τ и угол γ.
16. Окончание решение задачи.
Результаты исследования и их обсуждение
Геометрические параметры формы: S0 = 50 мм, R = 20 мм, φ = 150°.
Временные интервалы: \({\bar \Delta {\tau _n}}\): 0,01; 0,02; 0,03; 0,04; 0,05; 0,1; 0,2; 0,3; 0,4; 0,5; 2,0; 5,0; 6,0; 8,0; 9,0 с; P1 = 1 кг/cм2.
Разбиение области N1×N2 = 13×20.
Как показали расчеты, разбивка области на 13×20 элементов по первой и второй координатной оси у формы без выточек вполне пригодна для анализа проводимых расчетов. Аналогично и у формы с выточками, разбивка на 13×20 элементов по тем же координатным осям тоже вполне оправдана.
Параметры разливаемой стали при θ > 1000 °C (\(\theta _{\rm{м}}^*\) = 1000 °C):
G2 = 104 МПа; α1, 2 = 12·10–6 °С‒1; λ = 0,0298 Вт/(мм·°C); L1 = 270·103 Дж/кг (скрытая теплота плавления); C1, 2 = 444 Дж/(кг·°C); γ1 = 7,80·10–6 кг/мм3; θк = 1450 °C. | (8) |
Физические свойства металлической формы такие же, как и в (8), но
\[{G_3} = 81{\rm{ }}000\left[ {1 - 1,2{{\left( {\frac{Q}{{1000}}} \right)}^2}} \right]{\rm{МПа}}{\rm{.}}\] | (9) |
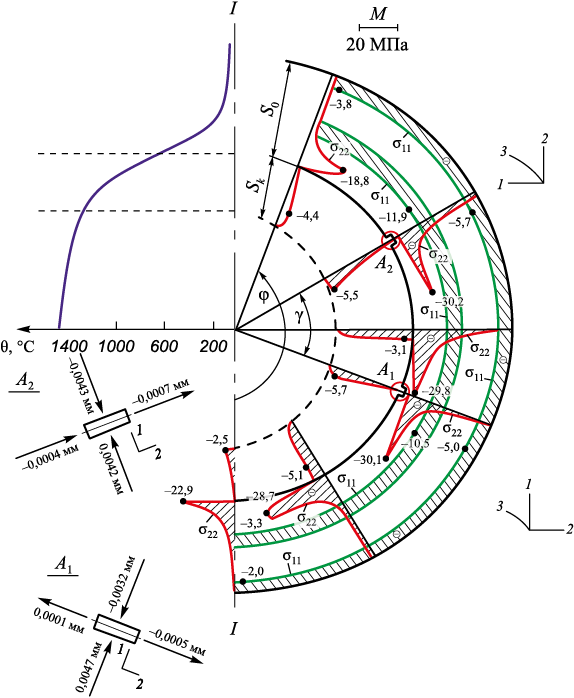
Начальные значения процесса оптимизации \(\bar \Delta {\varphi _0}\) = 23°, γ0 = 104°; размеры выточек A1 , A2 (7,1×2,6) мм в направлении осей 1 и 2 (рис. 3). Размеры выточек соответствуют размерам элементов сетки.
Рис. 3. Эпюры нормальных напряжений σ11 , σ22 и перемещений U1 , U2 |
В результате расчетов по приведенному выше алгоритму получено:
F = 29,8 МПа; γ = 60°; τ = 8,6 с. | (10) |
На рис. 3 приведены эпюры σ11 , σ22 и перемещения U1 , U2 по граням выточек A1 , A2 в форме. Видим, что по внутренним углам выточек A1 , A2 имеют место концентраторы напряжений σ22 , соответственно равные –30,1 и –30,2 МПа, которые несколько выше (по модулю), чем найденное значение F. Для сравнения на рис. 4 приведены эпюры напряжений σ22 , МПа, по сечению формы, не имеющей выточек; время то же – 8,6 с. Напряжение σ33 не приведено, так как оно примерно равно напряжению σ22 с разницей ±1 %.
Рис. 4. Эпюры нормальных напряжений σ22 по сечению формы |
Видна существенная разница по напряжениям σ22 .
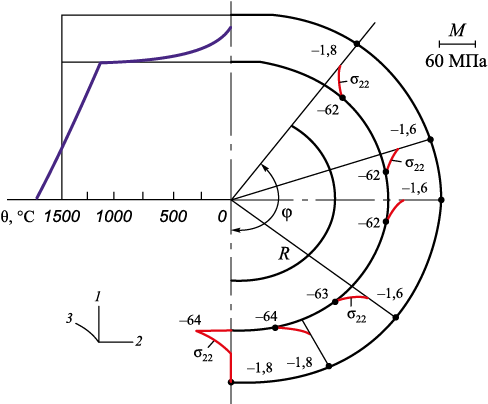
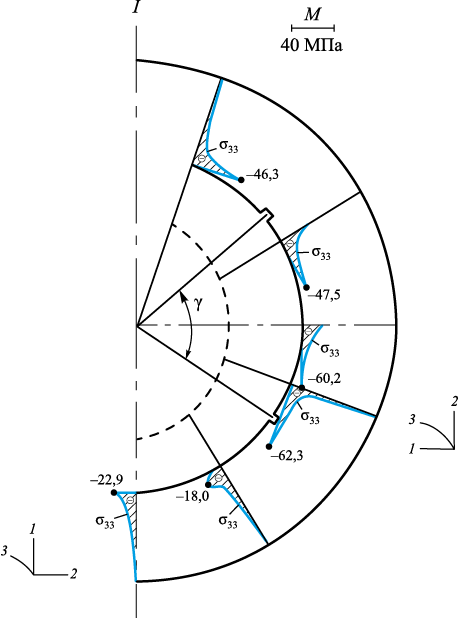
На рис. 5 приведены эпюры напряжений σ33 для найденных параметров (10).
Рис. 5. Эпюры нормальных напряжений σ33 в форме |
Хотя напряжения σ33 по многим сечениям уменьшились (по модулю), но на большом участке сжимающие напряжения довольно значительны (более 60 МПа). Следовательно, необходимо было оптимизацию вести как по σ22 , так и по σ33. Напряжение σ22 было взято, так как выточки в форме как бы прорезают их значительные значения на поверхности S3 в момент начального процесса охлаждения (рис. 4), не влияя на осевую симметрию. По всей видимости, для глобального снижения сжимающих напряжений σ22 и σ33 необходимо делать в форме дополнительные выточки, перпендикулярные заданным.
Но это уже другая задача (не осесимметричная), с другими уравнениями и другими граничными условиями.
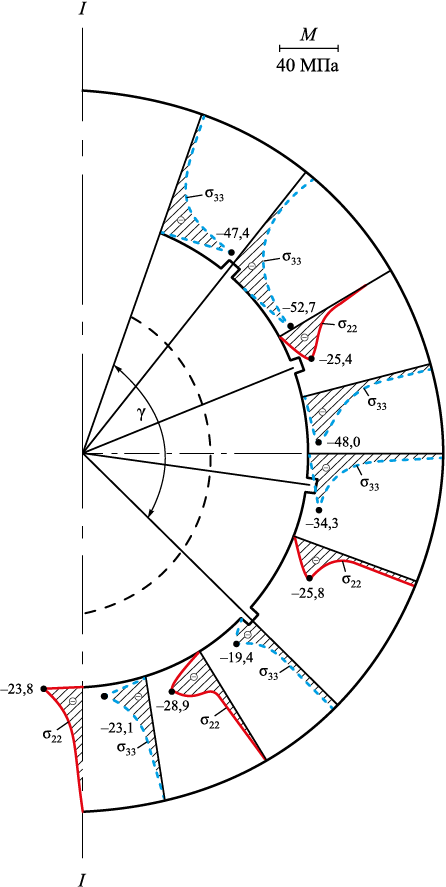
В рамках настоящей работы проведена попытка понизить (по модулю) напряжения σ33 , введя дополнительные выточки на поверхности S2 . По результатам полученного решения (10) следует, что выточки расположены на поверхности S2 симметрично по углу φ с углом раствора γ (рис. 2). При этом наибольшие (по модулю) напряжения σ33 как раз имеют место внутри раствора угла γ (рис. 5). Введем дополнительно еще две выточки на поверхности S2 внутри найденного угла γ. Проведем расчет НДС оболочечной стальной формы с заданными четырьмя выточками на поверхности S2 по приведенному выше алгоритму до τ = 8,6 с. Алгоритм значительно упрощается, так как расположение выточек фиксировано и время охлаждения задано. На рис. 6 приведены результаты расчета σ22 и σ33 по сечению формы на конец временного шага τ* = 8,6 с. Наблюдаем значительное снижение (по модулю) напряжений σ22 , а также снижение (по модулю) напряжений σ33 .
Рис. 6. Эпюры расчетных значений нормальных напряжений |
Таким образом, новизной настоящей работы является постановка задачи по установлению расположения температурных швов как технологически важных областей, так и значений напряжений в сферической металлической форме в условиях целевой функции min–max, а также алгоритм решения.
Предложенные методика, алгоритм моделирования и оптимизации стойкости сферических металлических форм к трещинообразованию могут быть использованы при численном решении других задач для различных функциональных оболочек.
Выводы
Поставлена и решена задача оптимизации конструктивных параметров температурных швов в сферической металлической литейной форме при заливке в нее расплавленного металла. При анализе НДС выявлены конструктивные особенности литейной металлической формы сферической конфигурации.
Наличие температурных швов на поверхности соприкосновения внутренней части формы с жидким металлом значительно снижает влияние возникающих температурных напряжений в первые моменты охлаждения отливки.
Определены рациональные области расположения температурных швов в ОФ и значения напряжений в них в условиях целевой функции min-max и разработанного алгоритма решения.
Список литературы
1. Евстигнеев А.И., Дмитриев Э.А., Одиноков В.И., Чернышова Д.В., Евстигнеева А.А., Иванкова Е.П. О трещиностойкости керамической оболочковой формы по выплавляемым моделям при затвердевании в ней шарообразной стальной отливки. Литейное производство. 2022;(9):17–21.
2. Литейное производство: Учебник для металлургических специальностей вузов / А.М. Михайлов, Б.В. Бауман, Б.Н. Благов и др. Москва: Машиностроение; 1987:256.
3. Голофаев А.Н. Расчет напряженно-деформированного состояния кокилей методом конечных элементов. Литейное производство. 1983;(5):16.
4. Дембовский В.В. Численное моделирование процессов формирования отливок в металлических формах. Литейное производство. 1992;(6):31–32.
5. Огородникова О.М. Напряженно-деформированное состояние металла в эффективном интервале кристаллизации. Литейное производство. 2012;(9):21–24.
6. Десницкая Л.В., Десницкий В.В., Матвеев И.А. Учет напряженно-деформированного состояния кристаллизующихся стальных отливок в технологии их производства. Литейное производство. 2019;(4):6–8.
7. Gamer U. On the elastic-plastic deformation of a sphere subjected to As spherically symmetrical temperature field. Journal of Thermal Stresses. 1988;11(3):159–173. https://doi.org/10.1080/01495738808961930
8. Kholdi M., Loghman A., Ashrafi H., Arefi M. Analysis of thick-walled spherical shells subjected to external pressure: Elastoplastic and residual stress analysis. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications. 2019;234(1):146442071988295. https://doi.org/10.1177/1464420719882958
9. Güven U. On stress distributions in functionally graded isotropic spheres subjected to internal pressure. Mechanics Research Communications. 2001;28(3):277–281. https://doi.org/10.1016/s0093-6413(01)00174-4
10. Ootao Y., Ishihara M. Transient thermoelastic analysis for a multilayered hollow cylinder with piecewise power law nonhomogeneity due to asymmetric surface heating. Acta Mechanica. 2014;225(10):2903–2922. https://doi.org/10.1007/s00707-014-1204-3
11. Saiyan S.G., Paushkin A.G. Development and verification of the two-layer thick-walled spherical shell’s finite element model under temperature and force exposure. IOP Conference Series: Materials Science and Engineering. 2020;913(3):032058. https://doi.org/10.1088/1757-899X/913/3/032058
12. Miller G.K. Stresses in a spherical pressure vessel undergoing creep and dimensional changes. International Journal of Solids and Structures. 1995;32(14):2077–2093. https://doi.org/10.1016/0020-7683(94)00197-5
13. Karami K., Abedi M., Zamani Nejad M., Lotfian M.H. Elastic analysis of heterogeneous thick-walled spherical pressure vessels with parabolic varying properties. Frontiers of Mechanical Engineering. 2012;7(4):433–438. https://doi.org/10.1007/s11465-012-0336-1
14. Abdelsalam O.R. Design optimization for a three-layers shrink-fitted pressure vessel exposed to very high pressure. IOP Conference Series: Materials Science and Engineering. 2019;610:012077. https://doi.org/10.1088/1757-899x/610/1/012077
15. Vitucci G., Mishuris G. Analysis of residual stresses in thermoelastic multilayer cylinders. Journal of the European Ceramic Society. 2016;36(9):2411–2417. https://doi.org/10.1016/j.jeurceramsoc.2015.12.003
16. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И., Намоконов А.Н., Чернышова Д.В., Евстигнеева А.А. Моделирование напряженно-деформированного состояния и оптимизация угла охвата сферической оболочковой формы опорным наполнителем. Прикладная механика и техническая физика. 2025;(1):189–196. https://doi.org/10.15372/PMTF202415455
17. Математическое моделирование сложных технологических процессов / В.И. Одиноков, Б.Г. Каплунов, А.В. Песков, А.В. Баков. Москва: Наука; 2008:178.
18. Алексеев Г.В., Левин В.А., Терешко Д.А. Моделирование и оптимизация в задачах проектирования сферических слоистых тепловых оболочек. Прикладная механика и техническая физика. 2019;60(2):158–168. https://doi.org/10.15372/PMTF20190213
19. Чзан Ю., Цзинь Ч., Пан М. Пластическая неустойчивость сферического сосуда высокого давления из ортотропного материала, нагруженного внутренним импульсным давлением. Прикладная механика и техническая физика. 2022;63(2):192–196. https://doi.org/10.1134/S0021894422020183
20. Алексеев Г.В., Соболева О.В., Терешко Д.А. Задачи идентификации для стационарной модели массопереноса. Прикладная механика и техническая физика. 2008;49(4(290)):24–35.
21. Евстигнеев А.И., Дмитриев Э.А., Чернышова Д.В., Одиноков В.И., Евстигнеева А.А., Иванкова Е.П. Моделирование внешнего силового воздействия на стойкость оболочковой формы при заливке в нее стали. Математическое моделирование. 2022;34(5):61–72. https://doi.org/10.20948/mm-2022-05-04
22. Евстигнеев А.И., Одиноков В.И., Дмитриев Э.А., Свиридов А.В., Иванкова Е.П. Влияние внешнего теплового воздействия на напряженное состояние оболочковых форм по выплавляемым моделям. Математическое моделирование. 2021;33(1):63–76. https://doi.org/10.20948/mm-2021-01-05
Об авторах
А. И. ЕвстигнеевРоссия
Алексей Иванович Евстигнеев, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Д. В. Чернышова
Россия
Дарья Витальевна Чернышова, аспирант кафедры «Авиастроение»
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
В. И. Одиноков
Россия
Валерий Иванович Одиноков, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Э. А. Дмитриев
Россия
Эдуард Анатольевич Дмитриев, д.т.н., доцент, ректор
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
А. А. Евстигнеева
Россия
Анна Алексеевна Евстигнеева, магистрант кафедры «Прикладная математика»
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Ю. Б. Колошенко
Россия
Юлия Борисовна Колошенко, старший преподаватель кафедры «Авиастроение»
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Д. А. Потянихин
Россия
Дмитрий Андреевич Потянихин, к.ф.-м.н., доцент кафедры «Авиастроение»
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Рецензия
Для цитирования:
Евстигнеев А.И., Чернышова Д.В., Одиноков В.И., Дмитриев Э.А., Евстигнеева А.А., Колошенко Ю.Б., Потянихин Д.А. Моделирование и оптимизация влияния температурных швов на напряженно-деформированное состояние сферических металлических литейных форм. Известия высших учебных заведений. Черная Металлургия. 2025;68(4):372-382. https://doi.org/10.17073/0368-0797-2025-4-372-382
For citation:
Evstigneev A.I., Chernyshova D.V., Odinokov V.I., Dmitriev E.A., Evstigneeva A.A., Koloshenko Yu.B., Potyanikhin D.A. Modeling and optimization of the effect of temperature seams on stress-strain state of spherical metal casting molds. Izvestiya. Ferrous Metallurgy. 2025;68(4):372-382. https://doi.org/10.17073/0368-0797-2025-4-372-382