Перейти к:
Расчет температуры и термоупругих напряжений в бойках при получении стальных полых заготовок на установке совмещенного литья и деформации. Часть 1
https://doi.org/10.17073/0368-0797-2025-4-366-371
Аннотация
В статье решается задача определения температуры калиброванных бойков установки совмещенного литья и деформации при получении стальных полых заготовок. Авторы обосновывают актуальность определения температурных полей и термоупругих напряжений в калиброванных бойках при обжатии стенки полой заготовки и на холостом ходу при охлаждении бойков водой, приводят прочностные и теплофизические свойства стали, из которой изготовлены бойки. Показана геометрия бойка для получения полой заготовки за один проход. Приводятся исходные данные для расчета температурного поля бойка установки совмещенного литья и деформации при получении полых заготовок, а также представлены температурные граничные условия для расчета температурных полей бойков. Статья описывает граничные условия для определения температуры бойка и значения теплового потока и эффективного коэффициента теплоотдачи. Результаты расчета температурных полей были выполнены в четырех сечениях для характерных линий и точек, расположенных на контактной поверхности бойка и в приконтактном слое на глубине 5 мм от рабочей поверхности. Размеры сетки конечных элементов приведены для использования при расчете температурного поля бойков. Температурное поле бойков с буртами определялось на основе решения уравнения нестационарной теплопроводности с соответствующими начальными и граничными условиями. Представлены величины и закономерности распределения температуры в калиброванном бойке при обжатии стенки полой заготовки и на холостом ходу при получении за один проход полой заготовки на установке совмещенного литья и деформации.
Ключевые слова
Для цитирования:
Лехов О.С., Билалов Д.Х. Расчет температуры и термоупругих напряжений в бойках при получении стальных полых заготовок на установке совмещенного литья и деформации. Часть 1. Известия высших учебных заведений. Черная Металлургия. 2025;68(4):366-371. https://doi.org/10.17073/0368-0797-2025-4-366-371
For citation:
Lekhov O.S., Bilalov D.Kh. Calculation of temperature and thermoelastic stresses in strikers during production of hollow steel billets in a unit of combined casting and deformation. Part 1. Izvestiya. Ferrous Metallurgy. 2025;68(4):366-371. https://doi.org/10.17073/0368-0797-2025-4-366-371
Введение
Технология получения стальных полых заготовок на трубных заводах отличается высокими капитальными, энергетическими и эксплуатационными затратами, поскольку включает литье сплошных круглых заготовок на горизонтальных машинах непрерывной разливки стали, их нагрев в печах и прошивку на прессах или валковых прошивочных станах. Следует отметить, что это оборудование в основном зарубежного исполнения и в условиях антироссийских санкций его поставки могут быть прекращены. В связи с этим разработана отечественная установка совмещенного процесса непрерывного литья и деформации, которая успешно заменяет зарубежное оборудование, ее можно использовать для получения стальных полых заготовок за один проход [1 ‒ 3]. Наиболее нагруженными элементами установки при получении полых заготовок являются калиброванные бойки, которые во время рабочего хода одновременно обжимают стенку полой заготовки и вытягивают ее из кристаллизатора. При этом в калиброванных бойках возникают суммарные напряжения от усилия обжатия и температурной нагрузки, которые снижают стойкость бойков. Для обоснованного выбора конструктивных параметров и материала калиброванных бойков необходимо определить их напряженное состояние при получении полых заготовок на установке совмещенного литья и деформации. Для этого необходимо определить температурное поле и термоупругие напряжения в бойках при обжатии стенки полой заготовки [4 ‒ 6].
В настоящей работе приведена методика расчета температурных полей и термоупругих напряжений в бойках установки совмещенного литья и деформации. Материал трубной заготовки – сталь марки 09Г2С; внутренний и наружный диаметры трубной заготовки 60 и 100 мм соответственно. Угловая скорость эксцентриковых валов 40 об/мин. При такой скорости время контакта бойка при рабочем ходе составляет 0,375 с, время паузы – 0,375·3 = 1,125 с. Температура трубной заготовки в зоне входа в боек 1200 °С, а после выхода из бойков 1000 °С.
Материал бойка – сталь инструментальная штампованная 4Х4ВМФС. Для расчета для этой стали в интервале температур от 20 до 700 °С принимали модуль упругости Е, плотность ρ, теплопроводность λ, теплоемкость с, коэффициент линейного расширения α и предел текучести σт [2].
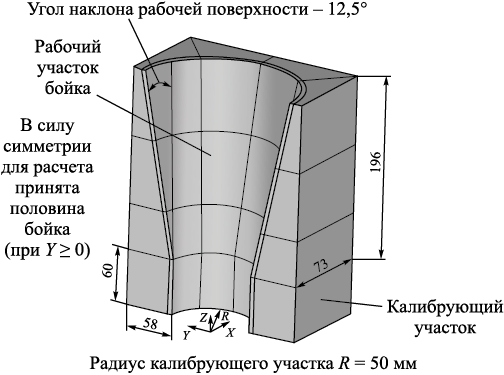
Геометрия бойка с размерами представлена на рис. 1.
Рис. 1. Геометрия бойка с размерами |
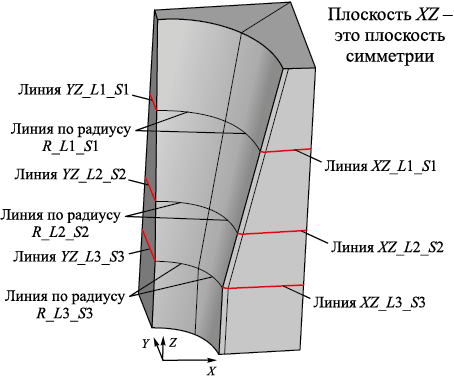
В силу симметрии расчет выполняли для половины бойка (рис. 2). Приведена часть видимых линий, для которых будут ниже приведены результаты расчета
Рис. 2. Геометрия половины бойка (часть видимых линий) |
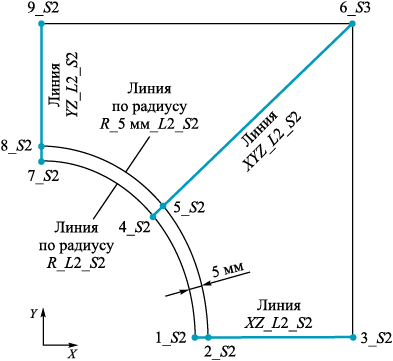
Результаты расчета температур и напряжений приведены для трех сечений (1, 2 и 3), в каждом сечении результаты представлены для пяти линий. Положение сечений, линий для каждого сечения, а также точек, через которые проходят линии по этим сечениям, представлены на рис. 3. В табл. 1 приведены наименования всех линий, а также указаны точки, через которые проходят эти линии.
Рис. 3. Положение точек и линий в сечении 2
Таблица 1. Наименования линий для трех сечений, точки,
| ||||||||||||||||||||||||||||||||||||||||||
Расчеты теплового и напряженного состояний бойков для каждой тепловой нагрузки (граничных условий теплообмена), заданных теплофизических и механических свойств материала бойков, а также геометрии бойков выполняли в следующей последовательности:
1. При принятом тепловом элементе SOLID 70, заданных граничных условиях теплообмена и теплофизических параметрах (плотности, теплопроводности, теплоемкости) материала бойка определяли квазиустановившееся температурное поле бойка в конце обжатия и в конце паузы [7 ‒ 9].
2. При принятом структурном элементе SOLID 185, модуле упругости и коэффициенте Пуассона, а также температурном поле в конце рабочего хода (из решения задачи на первом этапе) определяли термонапряженное состояние бойка в конце рабочего хода в направлении длины бойка [10 ‒ 12].
Температурное поле бойков определяется на основе решения уравнения нестационарной теплопроводности с соответствующими начальными и граничными условиями с использованием пакета ANSYS [10]:
| \[c{\rm{\rho }}\frac{{dT}}{{dt}} = \sum\limits_{i = 1}^3 {\frac{\partial }{{\partial {x_i}}}} \left( {\lambda \frac{{\partial T}}{{\partial {x_i}}}} \right),\] | (1) |
Все коэффициенты принимаем в зависимости от температуры бойков.
Начальное условие для функции T(\(\vec X\), t) имеет вид:
| \[T(\vec X,{\rm{ }}t) = {T_0}(\vec X).\] | (2) |
Начальная температура бойков 20 °С.
Для рабочей поверхности бойка граничные условия второго рода
| \[{\left. {{\rm{\lambda }}\frac{{\partial T}}{{\partial n}}} \right|_S}(t) = q,\] | (3) |
где q – плотность теплового потока от металла очага деформации.
В период паузы для рабочей поверхности бойка граничные условия третьего рода имеют вид
| \[\lambda \frac{{\partial T}}{{\partial n}} = - {\alpha _1}(T - {T_{\rm{к}}}),\] | (4) |
где α1 – эффективный коэффициент теплоотдачи на рабочую поверхность во время паузы; Тк = 60 °С – температура воды, подающейся на рабочую поверхность бойков во время паузы.
На торце бойка, задней стенке, сверху и снизу бойка граничные условия третьего рода имеют вид
| \[\lambda \frac{{\partial T}}{{\partial n}} = - {\alpha _2}(T - {T_{\rm{в}}}),\] | (5) |
где α2 – коэффициент теплоотдачи при охлаждении задней стенки, верха и низа бойка водой или воздухом в зависимости от варианта расчета; Тв = 60 °С – температура окружающей среды со стороны торца бойка, задней стенки, верха и низа бойка.
В такой постановке одним из допущений является то, что при расчете температурных полей бойков пренебрегаем тепловым потоком от излучаемого металла [13 ‒ 15].
Уравнения (1) – (5) образуют начальную краевую задачу определения нестационарного поля температур для бойков установки совмещенного процесса непрерывного литья и деформации [16 ‒ 18].
Такая схема определения температуры и термоупругих напряжений в бойках установки методом конечных элементов реализована в одном из модулей пакета ANSYS [19; 20].
Значения температур во всех точках линий приведены в табл. 2.
Таблица 2. Значения температур во всех точках линий |
| Сечение 1 | Сечение 2 | Сечение 3 | ||||||
| Точка | Температура, °С | Точка | Температура, °С | Точка | Температура, °С | |||
| ОХЛ | ТР | ОХЛ | ТР | ОХЛ | ТР | |||
| 1_S1 | 370 | 451 | 1_S2 | 365 | 445 | 1_S3 | 354 | 435 |
| 2_S1 | 392 | 392 | 2_S2 | 386 | 386 | 2_S3 | 373 | 373 |
| 3_S1 | 370 | 370 | 3_S2 | 350 | 350 | 3_S3 | 310 | 310 |
| 4_S1 | 368 | 448 | 4_S2 | 360 | 441 | 4_S3 | 348 | 429 |
| 5_S1 | 389 | 389 | 5_S2 | 381 | 381 | 5_S3 | 366 | 366 |
| 6_S1 | 344 | 344 | 6_S2 | 330 | 330 | 6_S3 | 285 | 285 |
| 7_S1 | 304 | 385 | 7_S2 | 294 | 375 | 7_S3 | 289 | 370 |
| 8_S1 | 314 | 314 | 8_S2 | 302 | 302 | 8_S3 | 295 | 295 |
| 9_S1 | 286 | 286 | 9_S2 | 252 | 252 | 9_S3 | 221 | 221 |
| Примечание. ОХЛ и ТР ‒ температура в конце паузы и в конце рабочего хода. | ||||||||
Анализ результатов расчета
От воздействия теплового потока во время обжатия заготовки температура контактной поверхности бойка составляет 370 ‒ 451 °С (результаты представлены только для части бойка между сечениями 1 – 3, табл. 1, точки 7_S3 и 1_S1). Максимум температуры находится в сечении 1 на плоскости симметрии бойка. Далее на холостом ходу при охлаждении бойка водой температура контактной поверхности бойка снижается и находится в диапазоне 289 ‒ 370 °С (точки 7_S3 и 1_S1). Максимум температуры находится в сечении 1 на плоскости симметрии бойка.
На глубине 5 мм температуры в конце контакта и в конце паузы при квазиустановившемся режиме одинаковые и зависят только от места положения, диапазон температур 295 ‒ 392 °С (точки 8_S3 и 2_S1). Максимум температуры находится в сечении 1 на плоскости симметрии бойка.
Характер изменения температур как по толщине бойка, так и по радиусу подобен. Максимум температур в контакте и в паузе на рабочей поверхности бойка и на глубине 5 мм находится в части бойка, расположенной ближе к кристаллизатору; к калибрующему участку температура снижается. Изменение температуры по радиусу: максимум на плоскости симметрии; снижение к боковой поверхности бойка.
Температура бойка по толщине уменьшается, на поверхности со стороны суппорта составляет 285 ‒ 370 °С (точки 6_S3 и 3_S1). Со стороны боковой поверхности бойка температура составляет 221 ‒ 286 °С (точки 9_S3 и 9_S1).
Выравнивание температур наступает на глубине 2 мм от контактной поверхности бойка, что имеет место как по толщине бойка, так и по его радиусу.
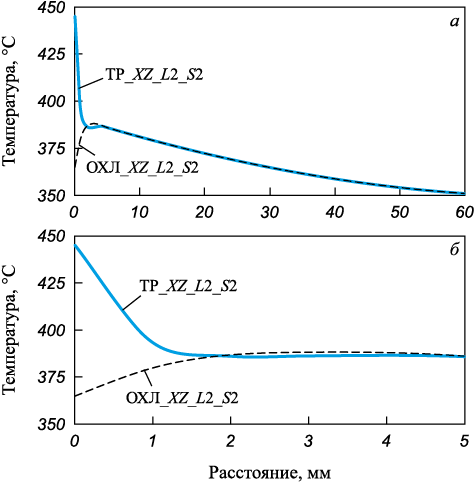
На рис. 4 и 5 показано распределение температуры по характерным линиям калиброванного бойка в сечении 2 при обжатии заготовки и на холостом ходу при охлаждении бойка водой. Следует отметить, что температуры в характерных точках сечений 1 и 2 бойка отличаются незначительно (табл. 2).
Рис. 4. Характер температур вдоль линии XZ_L2_S2
Рис. 5. Характер температур вдоль линии R_L2_S2 |
Выводы
Разработана методика расчета температурных полей и термоупругих напряжений в калиброванных бойках установки совмещенного литья и деформации при получении стальных трубных заготовок. Определено распределение температур по характерным линиям калиброванного бойка при обжатии заготовки и на холостом ходу при охлаждении бойка водой. Установлено, что от воздействия теплового потока во время обжатия заготовки температура контактной поверхности бойка составляет 370 – 451 °С.
Список литературы
1. Лехов О.С., Михалев А.В. Установка совмещенного процесса непрерывного литья и деформации для производства листов из стали для сварных труб. Теория и расчет. Екатеринбург: изд. УМЦ УПИ; 2017:151.
2. Лехов О.С., Михалев А.В., Шевелев М.М. Напряжения в системе бойки – полоса при получении листов из стали на установке непрерывного литья и деформации. Екатеринбург: изд. УМЦ УПИ; 2018:125.
3. Лехов О.С., Билалов Д.Х. Технологические возможности установок совмещенных процессов непрерывного литья и деформации для производства металлопродукции. Производство проката. 2016;(7):24–26.
4. Хлопонин В.Н., Косырева М.В., Косяк А.С. Влияние системы охлаждения на тепловые условия работы поверхностного слоя валка. В кн.: Труды МИСиС. Вып. 100. Москва: изд. МИСиС; 1977:90–93.
5. Боли Б., Уэйнер Дж. Теория температурных напряжений. Москва: Мир; 1976:349.
6. Лехов О.С. Исследование напряженно-деформированного состояния системы валки – полоса при прокатке широкополочной балки в клетях универсально-балочного стана. Сообщение 2. Известия вузов. Черная металлургия. 2014;57(12):15–19. https://doi.org/10.17073/0368-0797-2014-12-15-19
7. Кушнер В.С., Верещака А.С., Схиртладзе А.Г., Негров Д.А. Технологические процессы в машиностроении Ч. II. Обработка металлов давлением и сварочное производство. Омск: изд. ОмГТУ; 2005:200.
8. Буланов Л.В., Карлинский С.Е., Волегова В.Е. Долговечность роликов МНЛЗ при наружном и внутреннем охлаждении. В кн.: Надежность крупных машин. Сб. науч. тр. НИИтяжмаш. Свердловск: изд. НИИтяжмаш; 1990:126–132.
9. Лыков А.В. Теория теплопроводности. Москва: Высшая школа, 1967:600.
10. ANSYS. Structural Analysis Guide. Rel. 15.0.
11. Matsumia Т., Nakamura Y. Mathematical model of slab bulging during continuous casting. In: Applied Mathematical, and Physical Models in Iron and Steel Industry: Proceedings of the 3rd Process. Tech. Conf., Pittsburgh, Pa, 28-31 March 1982. New York; 1982:264–270.
12. Takashima Y., Yanagimoto I. Finite element analysis of flange spread behavior in H-beam universal rolling. Steel Research International. 2011;82(10):1240–1247. https://doi.org/10.1002/srin.201100078
13. Kobayashi S., Oh S.-I., Altan T. Metal Forming and Finite-Element Method. New York: Oxford University Press; 1989:377.
14. Karrech A., Seibi A. Analytical model of the expansion in of tubes under tension. Journal of Materials Processing Technology. 2010;210:336–362.
15. Kazakov A.L., Spevak L.F. Numeral and analytical studies of nonlinear parabolic equation with boundary conditions of a special form. Applied Mathematical Modelling. 2013; 37(10-13):6918–6928. https://doi.org/10.1016/j.apm.2013.02.026
16. Jansson N. Optimized sparse matrix assembly in finite element solvers with one-sided communication. In: High Performance Computing for Computational Science – VECPAR 2012. Berlin, Heidelberg: Springer; 2013:128–139.
17. Park C.Y., Yang D.Y. A study of void crushing in large forgings II. Estimation of bonding efficiency by finite-element analysis. Journal of Materials Processing Technology. 1997;72(1):32-41.
18. Sorimachi K., Emi T. Elastoplastic stress analysis of bulging as a major cause of internal cracks in continuously cast slabs. Tetsu-to-Hagane. 1977;63(8):1297–1304. https://doi.org/10.2355/tetsutohagane1955.63.8_1297
19. Marciniak Z., Duncan J.L., Hu S.J. Mechanics of Sheet Metal Forming. Oxford: Butterworth-Heinemann Elsevier Ltd.; 2002:228.
20. Fujii H., Ohashi T., Hiromoto T. On the formation of the internal cracks in continuously cast slabs. Tetsu-to-Hagane. 1978;18(8): 510–518. https://doi.org/10.2355/tetsutohagane1955.62.14_1813
Об авторах
О. С. ЛеховРоссия
Олег Степанович Лехов, д.т.н., профессор кафедры инжиниринга и профессионального обучения в машиностроении и металлургии
Россия, 620012, Екатеринбург, ул. Машиностроителей, 11
Д. Х. Билалов
Россия
Дамир Харасович Билалов, доцент кафедры инжиниринга и профессионального обучения в машиностроении и металлургии
Россия, 620012, Екатеринбург, ул. Машиностроителей, 11
Рецензия
Для цитирования:
Лехов О.С., Билалов Д.Х. Расчет температуры и термоупругих напряжений в бойках при получении стальных полых заготовок на установке совмещенного литья и деформации. Часть 1. Известия высших учебных заведений. Черная Металлургия. 2025;68(4):366-371. https://doi.org/10.17073/0368-0797-2025-4-366-371
For citation:
Lekhov O.S., Bilalov D.Kh. Calculation of temperature and thermoelastic stresses in strikers during production of hollow steel billets in a unit of combined casting and deformation. Part 1. Izvestiya. Ferrous Metallurgy. 2025;68(4):366-371. https://doi.org/10.17073/0368-0797-2025-4-366-371
JATS XML