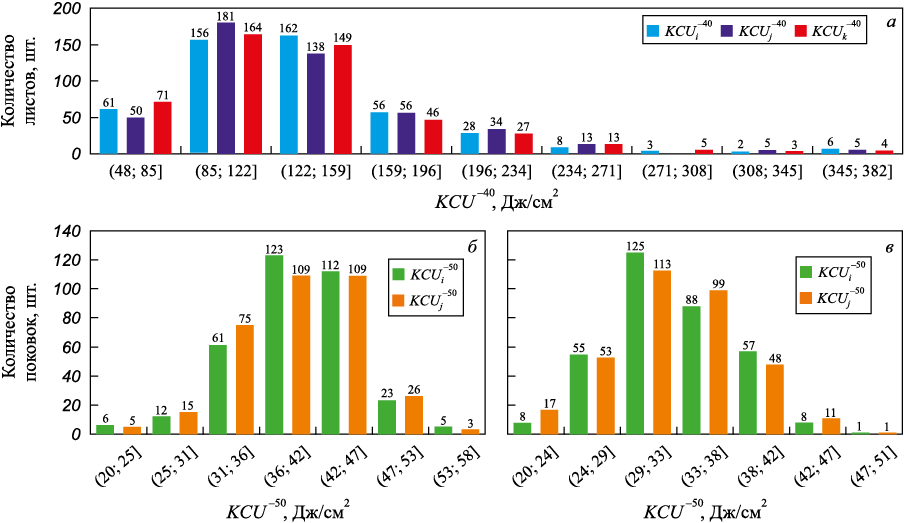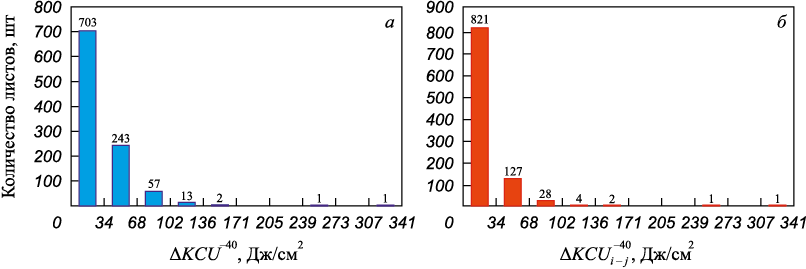O возможных последствиях, вызванных уменьшением количества образцов при приемо-сдаточных испытаниях единицы металлопродукции для оценки ее качества

Введение

Производство стали – сложный и многоступенчатый процесс, каждый этап которого хорошо оснащен средствами измерения и сбора информации. Уровень качества металлопродукции, в зависимости от ее назначения, обычно контролируется на основе определения ее механических свойств, оценки структуры и изломов. Объективность оценки важна также для решения обратной задачи: определения связи свойств со структурой, выделения критических параметров структуры, определяющих разброс качества металла, и выработки на этой основе технологических рекомендаций, направленных на повышение его однородности [1 – 2]. В этой связи, в частности, все больше применяются современные IT: нейросети, алгоритмы Big Data, машинного обучения и т. п. для обработки больших массивов данных производственного контроля процесса и продукта [3 – 6].

Логичен интерес к развитию методов оценки качества металлопродукции, особенно в связи с теми возможностями, которые появляются при цифровизации измерений структур и изломов, проведении и обработке результатов экспериментов [7 – 8]. Например, несмотря на десятилетние наработки в практике механических испытаний, не до конца ясно, как различие в количестве образцов при проведении приемо-сдаточных испытаний металлопродукции может сказаться на полноте ее оценки. В частности, учитывая широкий спектр неоднородных структур, формирующихся в рамках штатной отлаженной технологии и сопутствующий этому существенный разброс свойств, в первую очередь вязкости.

При определении качества металлопродукции на основе механических испытаний существуют различные подходы к выбору количества образцов на единицу продукции [9]. Такие стандарты могут устанавливать нормативные документы, например, ГОСТ 4543–2016 «Металлопродукция из конструкционной легированной стали» предусматривает отбор от каждого выбранного для контроля прутка, полосы или мотка по одному образцу для испытаний на растяжение, на ударный изгиб (каждого типа для соответствующих условий испытаний). Возможно также проведение испытаний с учетом условий соглашения между производителем и потребителем (с учетом назначения продукции). Обычно количество однотипных испытаний на контрольную единицу металлопродукции варьируется от одного до трех, максимальное значение, как правило, соответствует ударным испытаниям, которые сопровождаются большим разбросом значений. Нормы отбора образцов – результат «естественного отбора» в рамках испытательной практики, в своей основе функционируют уже достаточно длительное время. Консервативность норм отражает хронология дат их актуализации, например для ГОСТ 4543 это 1948, 1971 и 2016 гг.

По мере накопления представительных баз данных производственного контроля процесса и продукта на предприятиях, роста вычислительных мощностей, появления программных продуктов появилась возможность оценки различий в уровне аттестации качества металлопродукции при использовании разного количества образцов на единицу продукции. Неизбежность потери полезной информации при уменьшении объема испытаний очевидна, однако ее масштабы требуют своего уточнения. Это важно не только для понимания объективности оценки уровня аттестации качества металлопродукции, но и для выработки на ее основе обоснованных решений, направленных на коррекцию технологии в связи с наблюдаемым обычно на практике существенным разбросом значений приемо-сдаточных характеристик. Интерес к проблеме также определяется массовым характером механических испытаний и их вкладом в себестоимость металлопродукции.

Применение ретроспективного подхода при рассмотрении данной проблемы предусматривает также возможность учета статистической природы рассматриваемого объекта (большие массивы данных производственного контроля металлопродукции), в частности, обоснованного выбора соответствующих статистических инструментов как средства, повышающего объективность полученных оценок [10 – 11].

В связи с этим целью работы является оценка степени полноты информации, получаемой при вариации количества образцов в рамках механических испытаний единиц металлопродукции, как основы для повышения эффективности прогноза качества металла при статистическом анализе баз данных производственного контроля процесса и продукта в металлургии.

Объекты и методы исследования

В качестве объекта исследования были выбраны базы данных производственного контроля технологий получения крупных поковок переменного сечения из улучшаемой стали 38ХН3МФА-Ш и листа из стали 13Г1С-У (произведенных по принятым технологиям в течение одного-двух лет [1]). Базы данных производственного контроля представляли собой матрицу А_m×n, где строкам m соответствовало количество плавок (партий/поковок), столбцам n – значения технологических параметров (n_t) и характеристик качества металлопродукции (n_q). Для стали 38ХН3МФА-Ш количество строк в матрицах с привязкой к химическому составу после электрошлакового переплава составило m = 342 – поковки (из 40 исходных плавок), а для стали 13Г1С-У для толщин листа 8, 10 и 12 мм m = 751 (668 и 1281) – партий соответственно. Количество столбцов n в матрицах составило (n_t/n_q) 91/20 и 33/16 соответственно. Выходные параметры включали в себя, в частности, значения пределов прочности (σ_в), текучести (σ_0,2), относительного удлинения (δ) и ударной вязкости (KCU/KCV), полученные при различных температурах испытания. Тангенциальные образцы для механических испытаний из поковок стали 38ХН3МФА-Ш вырезались из торцевых темплетов с максимальным D_l и минимальным D_s диаметром, по два образца на каждую температуру испытания: на растяжение (при +20 °С) и удар: при +20 (KCU_i и KCU_j) и –50 °С (\(KCU_i^{ - 50}\) и \(KCU_j^{ - 50}\)). Из листовой стали 13Г1С-У от каждой партии отбиралось по одному поперечному образцу на растяжение (при комнатной температуре) и по три поперечных ударных образца (\(KCU_i^{ - 40}\), \(KCU_j^{ - 40}\), \(KCU_k^{ - 40}\) и \(KCV_i^0\), \(KCV_j^0\) и \(KCV_k^0\)) для испытаний при температурах –40 и 0 °С соответственно.

Статистическая оценка выборок (или партий) значений приемо-сдаточных параметров проводилась в программе Microsoft Excel на основе определения их максимальных (x_i max), минимальных (x_i min), средних \({\bar X_i}\) c ошибкой (s) и размаха (Δ = x_i max – x_i min) величин. Статистическую природу вида распределения значений параметров определяли на основе построения соответствующих гистограмм распределения значений, исходя из равномерной разбивки на разряды, число которых определялось как корень кубический из числа измерений [12], вычисления их коэффициентов асимметрии A_s и эксцесса E_x с соответствующими ошибками [13 – 14].

Сопоставление выборок проводили с использованием критериев Смирнова и Стьюдента (далее по тексту критерии С_n и C_p) с определением уровня риска выдвигаемых гипотез.

Результаты работы и их обсуждение

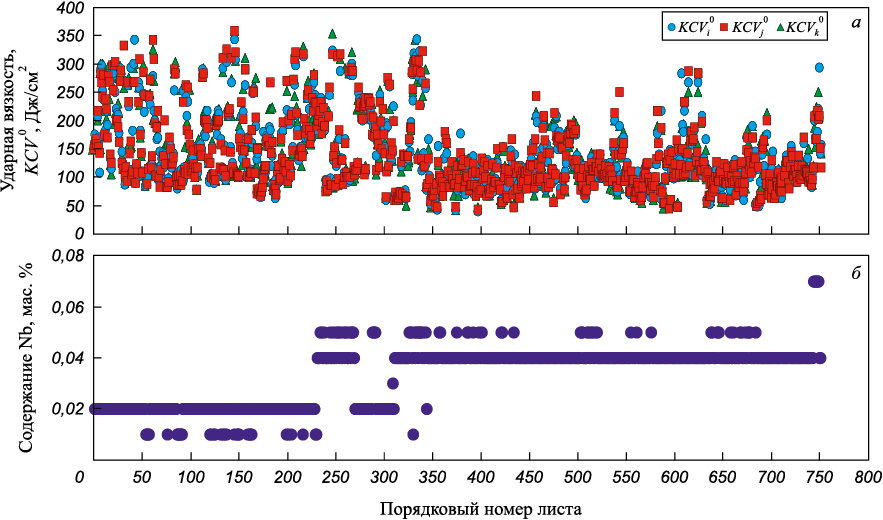
Нередко причиной отсутствия прогресса в применении современных программных решений при обработке больших массивов данных является недостаточное внимание к этапу работы, связанному с выявлением факторов, способных внести искажения, часто существенные, в дальнейшую статистическую обработку массивов данных. Это относится как к входным, так и выходным (результаты приемо-сдаточных испытаний) параметрам. Например, построение хронологических рядов значений характеристик качества металлопродукции и технологии позволило выявить в стали 13Г1С-У взаимосвязанные «сезонные» колебания ударной вязкости и содержания ниобия (рис. 1). Это означает, что исходная база данных фактически разделена на два подмассива: с низким (Nb ≤ 0,03 мас. %) и высоким (Nb ˃ 0,03 мас. %) содержанием ниобия, количество партий в которых для толщин 8, 10 и 12 мм составило: 269, 395, 260 и 489, 273, 1021 штук соответственно. Их совместный статистический анализ привел бы к усреднению как выходных, так и входных значений параметров. Это исказило бы действительный вид гистограмм распределения значений параметров и осложнило применение статистических инструментов, в частности регрессии. В этой связи последующий статистический анализ проводился раздельно для двух подмассивов данных, в работе же представлены его результаты для подмассива данных с содержанием ниобия более Nb ˃ 0,03 мас. %, как наиболее представительного по объему выборки.

Следует отметить, что подобные явления имеют весьма разнообразные формы проявления, и необязательно только применимо к ударной вязкости. Например, в хронологическом ряду значений условного предела текучести трубной стали (категории прочности К65 и толщиной стенки 27,7 мм), соответствующих левой и правой частям бимодальной гистограммы их распределения, наблюдалось последовательное их чередование [15].

Для всех исследуемых баз данных, структурированных подобным или иным образом (выявление трендов, удаление ошибок записи и т. п.), были определены основные статистические характеристики приемо-сдаточных параметров, которые выявили наличие существенного разброса механических свойств (табл. 1, 2).

Наибольший разброс значений свойств наблюдался для ударной вязкости (по сравнению с показателями прочности). Так, у стали 13Г1С-У максимальное значение вязкости превышало минимальное в 5 – 6 раз, а для стали 38ХН3МФА-Ш – в 2 раза (это было характерно и для других видов металлопродукции [10]). Такая неоднородность вязкости обусловлена различиями в сценариях протекания технологической наследственности – реализацией разнообразных механизмов эволюции структур и дефектов по технологической цепочке и, как следствие, многообразием морфологии номинально однотипных конечных структур [1; 16; 17]. Это предполагает необходимость объективной оценки масштабов разброса ударной вязкости, в связи с чем возможное различие в количестве испытываемых образцов (в данном случае применимо к отдельной поковке или партии листов) может оказаться существенным фактором, определяющим корректность оценки.

Однако сопоставление различных выборок по их средним значениям и размахам не всегда может дать полную информацию о масштабах неоднородности исследуемых характеристик качества металлопродукции. Так, например, большой размах может быть связан с наличием единичных выбросов, а средние значения и их дисперсии будут иметь смысл при нормальном характере распределения значений параметров качества [10]. Этим определялся интерес к построению их гистограмм распределения. Гистограммы строили отдельно для результатов первого {\(KCU_i^{ - 40}\)}, второго {\(KCU_j^{ - 40}\)} и третьего {\(KCU_k^{ - 40}\)} испытаний – сталь 13Г1С-У и первого {\(KCU_i^{ - 50}\)} и второго{\(KCU_j^{ - 50}\)} испытаний – сталь 38ХН3МФА-Ш, где номер испытания соответствовал определенному номеру столбца в матрице данных (рис. 2).

Для распределений значений ударной вязкости наблюдалось отклонение от нормального распределения. Его масштаб оценивали по соответствующим величинам коэффициентов асимметрии и эксцесса, их вариация была в достаточно широких пределах. Для стали 38ХН3МФА-Ш коэффициенты асимметрии A_s и эксцесса E_x значений ударной вязкости изменялись в пределах: \(\left[ {-0,43;-0,31} \right]\) и \(\left[ {0,70;0,80} \right]\) для темплетов диаметром D_s и \(\left[ {-0,31;0,35} \right]\) и \(\left[ {-0,14;0,23} \right]\) для темплетов диаметром D_l соответственно. Для распределений значений ударной вязкости KCV⁰ и KCU^–40 в стали 13Г1С-У, например, для листа толщиной 8 мм: \(\left[ {1,64;1,68} \right]\); \(\left[ {1,54;1,81} \right]\) и \(\left[ {3,12;3,40} \right]\); \(\left[ {3,40;5,29} \right]\) соответственно. Различие статистических показателей для результатов отдельных испытаний: {\(KCU_i^{ - 40}\)}, {\(KCU_k^{ - 40}\)}, {\(KCU_i^{ - 40}\)} и {\(KCV_i^0\)}, {\(KCV_j^0\)}, {\(KCV_k^0\)} (де-факто исходя из предположения, что ударную вязкость оценивали, испытывая по одному образцу на каждую единицу продукции – партию листа или поковку) – признак отличий в их статистической природе, а их абсолютные значения – мера отклонения от нормального вида распределения. Это, в частности, указывает на необходимость учета данного обстоятельства при выборе количества образцов, необходимого для аттестации качества металлопродукции.

При статистической обработке полученный результат во многом определяется объемом выборки данных [1; 13]. Для выборок с максимальным объемом данных V_i, имеющихся в распоряжении, была характерна минимальная ошибка определения коэффициентов асимметрии и эксцесса: 0,23 и 0,77 соответственно. При последовательном уменьшении объема выборок V_i, начиная со значения V_i = 200 – 250 для листов (в зависимости от толщины листа) и V_i = 150 – 200 для поковок, становится существенным разброс величин коэффициентов асимметрии и масштаб ошибки их определения. При дальнейшем уменьшении объема выборки, например, для значений ударной вязкости (KCU^–40, для всех трех образцов на партию) стали 13Г1С-У (лист толщиной 12 мм), значения коэффициента асимметрии A_s, рассчитанные по 20 выборкам (объемом 50 партий каждая), отобранным последовательно из исходной выборки объемом 1000 шт., варьировались в диапазоне –0,2 ≤ A_s ≤ 2,2 при погрешности определения 3,0. Очевидно, что при таких значениях вариации коэффициента A_s и ошибке его определения, статистические оценки не будут представительными. Подобное утверждение было справедливо и по отношению к выборкам ударной вязкости поковок из стали 38ХН3МФА-Ш.

В этой связи применение средних значений по выборкам в сочетании с критериями классической статистики для их сопоставления может внести неопределенность в получаемые оценки. Например, попарное сравнение между собой выборок значений ударной вязкости стали 13Г1С-У (взятых из полученных при штатном испытании трех образцов на партию результатов) (табл. 3) показало, что различие в уровне риска гипотезы о совпадении выборок при оценках по критериям Стьюдента и Смирнова [18] могло существенно отличаться (до 30 %). Фактически это означает, что для различных выборок ударной вязкости – трех сочетаний ее исходных результатов, полученных в рамках каждой партии (единицы продукции), может отличаться вид распределения значений вязкости, что указывает на различие в их статистической природе. В этой связи идентичность выборок не всегда можно подтвердить на основе критериев классической статистики (Стьюдента), а в ряде случаев привести к противоположным заключениям при применении одновременно критериев Стьюдента и Смирнова.

Очевидно, что применение двух образцов для испытания единицы продукции должно повысить полноту аттестации ее качества (по сравнению с одним образцом). Однако при этом неизбежны сложности при выборе значения, характеризующего показатель качества металлопродукции в целом. По двум значениям некорректно рассчитывать их среднее \({\bar X_i}\), так как одному и тому же среднему может соответствовать различный размах Δ между максимальным и минимальным значением, а образцам с одинаковыми значениями размаха – различный абсолютный уровень свойств (их медианное значение). Как вариант, для последующего статистического анализа может быть выбрано минимальное (худшее) значение вязкости, но предпочтительнее делать выбор на основе рассмотрения всех возможных вариантов оценки [19].

Из общих соображений, очевидно, что отбор трех образцов для испытания единицы продукции даст не только возможность оценить ошибку среднего s, но и позволит более объективно оценить неоднородность качества продукции и по величине среднеквадратичного отклонения, и по уровню размаха Δ.

Построение распределений величин размахов ΔKCU^–40 по результатам всех трех испытаний (для каждой партии листов из стали 13Г1С-У толщиной 12 мм) или возможных сочетаний пар результатов, выбранных из них (Δ_i–j, Δ_i–k и Δ_j–k – индексы соответствуют номерам столбцов в матрице данных), при единой разбивке на разряды, позволило их сопоставить (рис. 3).

Показано, что для всех гистограмм значений размахов характерна правосторонняя асимметрия. Это подтверждается расчетами коэффициентов асимметрии А_s и эксцесса Е_x (табл. 4).

Очевидно, что абсолютные значения коэффициентов асимметрии и эксцесса распределений размахов ударной вязкости трех образцов Δ = KCU_max – KCU_min оказались меньше, по сравнению со значениями размахов по каждой из трех пар образцов. Однако абсолютные значения размахов для трех образцов были больше парных размахов пар образцов Δ_i – j, Δ_i – k и Δ_j – k в 56,4 – 67,7 % случаев (для всех толщин и партий листов). Для парных сочетаний величины размахов минимизировались, большее количество попаданий наблюдалось в первом разряде, возможны были совпадения значений (нулевой размах), в последующих разрядах гистограммы количество значений размахов в 1,5 – 2,5 раз было меньше, по сравнению с гистограммой распределения размахов, полученных по результатам испытаний трех образцов. Все парные выборки значений размахов Δ_i – j, Δ_i – k и Δ_j – k (для ударной вязкости KCU^–40 и KCV⁰ листов толщиной 8, 10 и 12 мм) значимо отличались от исходной выборки – экспериментальные величины критериев Стьюдента и Смирнова были не менее 4,61 и 2,77 соответственно (риск менее 0,0001).

Однако при проверке значимости различий выборок размахов парных значений ударной вязкости KCU^–40 и KCV⁰ полного «единодушия» между результатами проверки по двум критериям уже не наблюдалось. В 9 вариантах сравнения пар из возможных 18 (три варианта выборок Δ_i – j, Δ_i – k и Δ_j – k для трех толщин листа 8, 10 и 12 мм и двух типов ударной вязкости KCU^–40 и KCV⁰ стали 13Г1С-У) риск гипотезы о различии выборок по двум критериям варьировался в интервале от 0,22 до 0,50. При сравнении 9 пар из 18 было выявлено их статистическое соответствие, в шести и трех случаях с риском не более 0,20 и 0,30 (хотя бы по одному из критериев) соответственно выборки пар отличались (для всех толщин листа и видов ударной вязкости).

По отношению к значениям ударной вязкости, полученным исходно на двух образцах, у показателя ударной вязкости третьего образца может быть другой вариант расположения (на соответствующей оси координат значений ударной вязкости): не только левее или правее минимального и максимального показателей вязкости соответственно, но и между ними (если они не совпадают), например, левее или правее медианного значения (для исходной пары результатов испытаний).

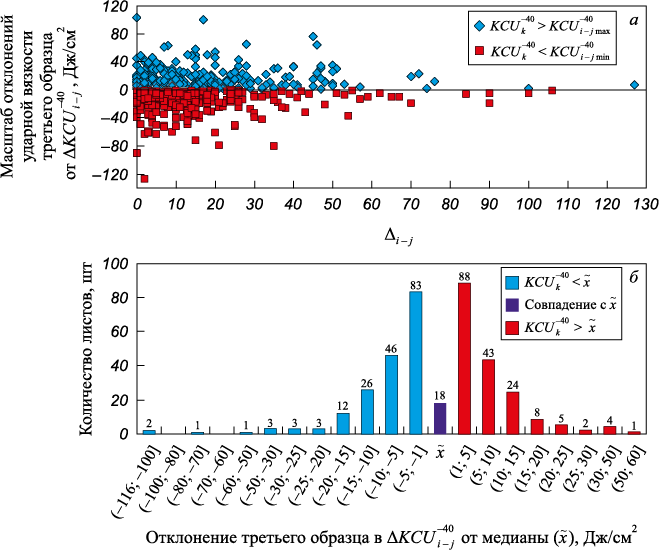
Статистика расположения значений ударной вязкости третьего образца \(KCU_k^{ - 40}\) (относительно соответствующих показателей пар образцов \(KCU_i^{ - 40}\) и \(KCU_j^{ - 40}\)) имела достаточно типичный характер. Например, для листов толщиной 12 мм из стали 13Г1С-У доля выходов ударной вязкости \(KCU_k^{ - 40}\) левее и правее границ интервала вязкости отдельных пар образцов [\(KCU_i^{ - 40}\); \(KCU_j^{ - 40}\)] была близкой (рис. 4, а). Очевидно, что даже при небольшом превышении границы этот результат может существенно изменить статистику медианных значений при их трансформации в средние значения (как в меньшую, так и в большую сторону), а при больших превышениях влияние таких отклонений становится еще сильнее. В интервал парных показателей ударной вязкости [\(KCU_i^{ - 40}\); \(KCU_j^{ - 40}\)] третий образец «попадал» от 373 до 402 раз (36,5 – 39,4 % от общего числа партий), из них от 180 до 184 показателей вязкости были меньше медианных значений \({\tilde x_i} = \frac{{KCU_i^{ - 40} + KCU_j^{ - 40}}}{2},\) а от 175 до 202 – больше (рис. 4, б). Совпадение с медианными значениями было в пределах от 1,6 до 1,8 % и фактически трансформировало его в среднее значение по партии, а все остальные показатели, так или иначе, изменяли оценку ударной вязкости партии. В целом, отсюда вытекает и масштаб рисков при обратных действиях в том случае, когда решается задача, связанная с уменьшением количества образцов, используемых для оценки ударной вязкости отдельных партий листа, с трех до двух единиц.

Однако в сталях с развитой неоднородностью структур далеко не всегда использование даже трех образцов для аттестации качества металлопродукции, в первую очередь вязкости, может обеспечить получение объективных оценок. Это, в частности, относится к сталям с сохранившейся литой структурой (крупные поковки из улучшаемой стали типа 38ХН3МФА-Ш, 15Х2НМФА), к высокопрочному прокату – листовые стали с феррито-перлитной, феррито-бейнитной полосчатостью в микроструктуре [7; 20 – 22]. Наличие развитой неоднородности морфологии разнородных структур, включая неметаллические включения (НВ), как от образца к образцу, так и в пределах отдельных образцов приводит к большому разбросу значений ударной вязкости, причем во всем диапазоне температур испытания. Это вносит неопределенность в оценку вязкости, в том числе и в определение хладостойкости.

В этой связи перспективным может оказаться использование микрообразцов, при сопоставимости габаритов которых с масштабом структурной неоднородности можно получить оценки хладостойкости отдельных структурных составляющих, ранжировать их по степени опасности, определяя энергию хрупкого разрушения по измерениям акустической эмиссии [7]. Это важно для понимания причин разброса вязкости при использовании стандартных схем испытаний. Именно такой подход позволил показать, что в крупных поковках из улучшаемой стали 38ХН3МФА-Ш в интервале от –130 до 100 °С хрупко разрушается только межосевое пространство, а ниже –130 °С хрупко разрушаются и оси дендритов. Различия же в рисунке дендритной структуры от одного ударного образца к другому (включая их дальние последствия в микроструктуре и морфологии НВ [1]) приводят к повышенному разбросу вязкости при всех температурах испытания и риску прогноза хладостойкости.

Для стали 15Х2НМФА такие испытания позволили уточнить диапазон температур вязко-хрупкого перехода с привязкой к механизму хрупкого разрушения (транскристаллитное, зернограничное и смешанное). Это важно для оценки возможной деградации хладостойкости металла в ходе длительной эксплуатации, когда ограничено число образцов-свидетелей, и при малом количестве образцов в рамках приемо-сдаточных испытаний.

Применение такого подхода оказалось полезным не только для оценки хладостойкости структурных составляющих, но и для определения степени опасности аномалий структур. Например, в высокопрочных трубных сталях категории прочности К65 микромеханические испытания позволили локализовать разрушение в пределах протяженной границы раздела в металле с образованием грубых фасеток поперечником порядка 500 мкм каждая, как одну из возможных причин расслоения (шиферности в изломе [20]), и оценить энергию ее разрушения по измерениям акустической эмиссии [7].

В целом, полученные результаты показывают, что такие факторы, как различная статистическая природа распределения значений результатов приемо-сдаточных испытаний (в том числе в рамках рассматриваемых хронологических рядов событий), отличие в широте «охвата» возможного разброса свойств в зависимости от количества образцов, испытываемых на единицу продукции при приемо-сдаточных испытаниях, возможность получения не совпадающих оценок гипотез при сопоставлении выборок с использованием различных статистических критериев, многообразие механизмов технологической наследственности, реализуемых в рамках штатной технологии получения металлопродукции, но изученных далеко не во всех случаях [1; 7], и многие другие причины в серьезной мере будут существенно сдерживать возможности эффективного применения современных программных решений при разработке систем сквозного управления качеством металлопродукции.

Достижение результатов в этом направлении должно базироваться на глубоком понимании закономерностей эволюции структуры и дефектов по всей технологической цепочке, развитии цифровых средств количественной оценки структур и изломов и их применением в производственной практике для повышения полноты аттестации качества металлопродукции, использовании статистических процедур с учетом понимания статистической природы объекта, а также с учетом необходимости поиска областей с доминирующим типом зависимости (в пределах пространства параметров технологии) и оценки их совместного взаимодействия [7; 15; 19].

Выводы

На основе статистического анализа представительных баз данных производственного контроля технологии получения листовой стали 13Г1С-У (толщина листа 8, 10 и 12 мм) и крупных поковок из улучшаемой стали 38ХН3МФА-Ш выделены факторы, определяющие различие в оценке их качества при приемо-сдаточных испытаниях с использованием различного количества образцов на единицу продукции (партия, поковка): вариация фиксируемого разброса свойств (размах значений); изменение статистической природы вида распределения значений свойств (вариация величин коэффициентов асимметрии и эксцесса); объем анализируемой выборки.

Показано, что при статистическом анализе баз данных производственного контроля существенное значение для исключения побочных эффектов, снижающих информативность результатов приемо-сдаточных испытаний, играет соответствующая подготовка массива данных, направленная на исключение влияния трендов, сезонных колебаний, выбросов и т. п.

Установлено, что снижение числа образцов при приемо-сдаточных испытаниях листовой стали 13Г1С-У с трех до двух (для каждой партии) приводит к увеличению количества минимальных значений размахов ударной вязкости Δ (от 0 до 34 Дж/см²) на 17 – 20 % и снижению количества размахов в диапазоне от 35 до 136 Дж/см² в 2,0 – 3,5 раза. Это искажает оценку масштаба неоднородности вязкости стали. Для стали 38ХН3МФА-Ш можно ожидать еще большего масштаба искажений с учетом развитой неоднородности морфологии структур (дендритной, микро- и НВ).

При вариации количества испытаний (при оценке качества единицы металлопродукции) и связанном с этим изменением вида распределения значений характеристик качества металлопродукции выборки в целом, возможно получение различных результатов проверки гипотез при сопоставлении выборок с использованием статистических критериев Стьюдента и Смирнова. Это следует учитывать при попытках применения современных программных продуктов (Big Data, машинное обучение и др.) в ретроспективном анализе баз данных производственного контроля в металлургии.