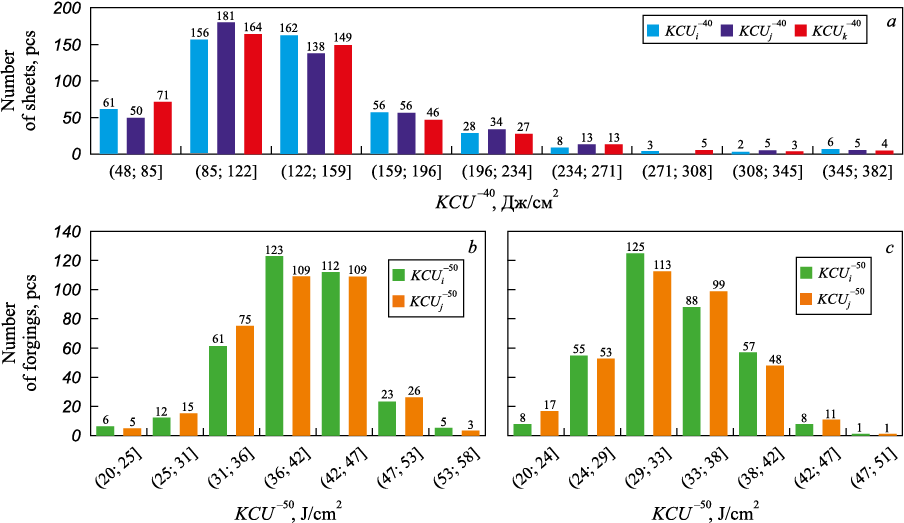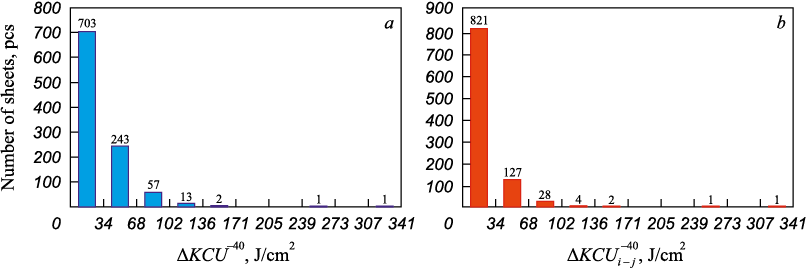Possible consequences caused by reducing the number of samples during acceptance tests of a unit of metal products to assess its quality

Introduction

Steel production is a complex, multi-stage process, with each stage well-equipped with tools for measurement and data collection. Depending on the intended application, the quality of metal products is typically assessed through mechanical testing, structural analysis, and fracture evaluation. Objective quality assessment is also essential for addressing the inverse problem – namely, establishing the relationship between structure and properties, identifying critical structural parameters responsible for variations in metal quality, and developing technological recommendations to improve product uniformity [1 – 2]. In this context, modern IT solutions – such as neural networks, Big Data algorithms, and machine learning – are increasingly used to process large datasets generated through production process and product quality control [3 – 6].

There is growing interest in enhancing methods for evaluating the quality of metal products, particularly given the new opportunities created by the digitalization of structural and fracture measurements and the automation of experimental data processing [7 – 8]. For example, despite decades of experience with mechanical testing, it remains unclear how variations in the number of test samples used in acceptance testing may affect the completeness of quality assessments – especially considering the wide range of heterogeneous structures that form under standard, well-established technologies and the significant resulting variability in properties, particularly impact strength.

Various approaches exist for determining the number of samples per unit of metal product during mechanical testing [9]. Such requirements may be specified in regulatory standards. For example, GOST 4543 – 2016 “Metal Products Made of Structural Alloy Steel” stipulates that one sample for tensile testing and one for impact testing (under each relevant test condition) must be taken from each bar, strip, or coil selected for quality control. In some cases, testing procedures are established by agreement between the manufacturer and the customer, based on the product’s intended use. Typically, the number of identical tests per control unit ranges from one to three, with impact testing usually performed at the upper limit due to the high variability of results. Sampling norms are the result of long-standing practical experience and have remained largely unchanged for decades. Their conservative nature is reflected in the update history of such standards – for example, GOST 4543 was revised in 1948, 1971, and 2016.

With the accumulation of representative production control databases, the growth of computational resources, and the development of specialized software tools, it has become possible to evaluate how changes in the number of test samples per product unit influence quality certification outcomes. While a reduction in the number of tests clearly leads to some loss of valuable information, the extent of that loss requires clarification. Understanding this is essential not only for evaluating the objectivity of quality assessments but also for making informed decisions on adjusting the technological process – particularly given the significant variation in acceptance testing results commonly observed in practice. Interest in this issue is also driven by the widespread use of mechanical testing and its contribution to the overall production cost of metal products.

A retrospective approach to this issue also allows for consideration of the statistical nature of the subject (i.e., large-scale production control datasets), making it possible to justify the selection of appropriate statistical tools that enhance the objectivity of the findings [10 – 11].

In this regard, the aim of this study is to assess the completeness of information obtained when varying the number of samples used in mechanical testing of individual metal product units. This analysis serves as a foundation for improving the effectiveness of metal quality forecasting through statistical analysis of production process and product control data in metallurgy.

Research objects and methods

This study was based on production control databases for two types of metal products manufactured using established technologies over one to two years: large, variable cross-section forgings made of heat-treatable 38KhN3MFA-Sh steel, and sheet products made of 13G1S-U steel [1]. Each database was structured as a matrix А_m×n, where the rows (m) corresponded to the number of heats (or batches/forgings), and the columns (n) included both technological parameters (n_t) and product quality characteristics (n_q). For 38KhN3MFA-Sh steel, the database contained m = 342 forgings derived from 40 individual heats, with the matrices linked to the chemical composition after electroslag remelting. For 13G1S-U sheet steel with thicknesses of 8, 10, and 12 mm, the number of batches was m = 751, 668, and 1281, respectively. the total number of columns n in the matrices was 91/20 and 33/16 for the two steels, corresponding to n_t/n_q values. the output parameters included, in particular, ultimate tensile strength (σ_u), yield strength (σ_0.2), elongation at break (δ), and impact strength (KCU/KCV), all measured at various test temperatures. Tangential mechanical test samples from 38KhN3MFA-Sh forgings were cut from end-face templates at maximum (D_l) and minimum (D_s) diameters. Two samples were tested per temperature condition: one for tensile testing at +20 °С , and two for impact strength at +20 (KCU_i and KCU_j) and –50 °С (\(KCU_i^{ - 50}\) and \(KCU_j^{ - 50}\)). From each batch of 13G1S-U sheet steel, one transverse sample was selected for tensile testing at room temperature, and three transverse samples were selected for impact strength testing at –40 °C and 0 °C, respectively (\(KCU_i^{ - 40}\), \(KCU_j^{ - 40}\), \(KCU_k^{ - 40}\) and \(KCV_i^0\), \(KCV_j^0\) and \(KCV_k^0\)).

Statistical evaluation of sample groups (or batches) of acceptance test parameters was performed using Microsoft Excel. For each group, the maximum (x_i max), minimum (x_i min), mean \({\bar X_i}\) (with standard deviation s) and range (Δ = x_i max – x_i min) were determined. the distribution type of each parameter was analyzed by constructing histograms using equal-width intervals. the number of intervals was set as the cube root of the number of measurements [12]. Skewness (A_s) and kurtosis (E_x) coefficients were then calculated, along with their respective standard errors [13 – 14].

Sample comparisons were performed using the Smirnov’s and Student’s tests (hereafter referred to as С_n and C_p, respectively), with the significance level of each hypothesis tested.

Results and discussion

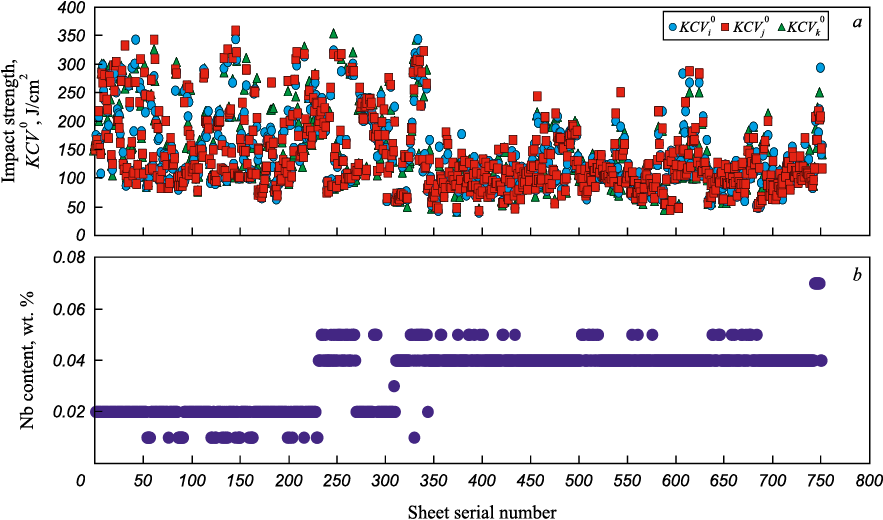
One of the main barriers to the effective use of modern software tools in processing large-scale datasets is the insufficient attention paid to identifying factors that can significantly distort the results of statistical analysis. These distortions may affect both input variables and output parameters – such as the results of acceptance testing. For example, when chronological series of quality characteristics and technological parameters were constructed for 13G1S-U steel, correlated “seasonal” fluctuations were observed in both impact strength and niobium content (Fig. 1). This pattern indicates that the original dataset is, effectively, divided into two distinct subsets: one with low niobium content (Nb ≤ 0.03 wt. %) and one with high content (Nb ˃ 0.03 wt. %). For sheet thicknesses of 8, 10, and 12 mm, the number of batches in the low-Nb subset was 269, 395, and 260, respectively; in the high-Nb subset, 489, 273, and 1021 batches. Conducting a combined statistical analysis of these subsets would result in averaging both input and output parameters, which would distort the actual shapes of the parameter distribution histograms and hinder the use of statistical tools such as regression analysis. Therefore, subsequent statistical processing was performed separately for the two subsets. the present paper reports the results for the subset with Nb ˃ 0.03 wt. %, as it was the more representative in terms of sample size.

It is important to emphasize that such effects are not unique to impact strength and may take various forms. For example, in a chronological series of yield strength values for pipe steel (strength category K65, wall thickness 27.7 mm), which correspond to the left and right peaks of a bimodal distribution histogram, a consistent alternation of values over time was observed [15].

For all datasets – regardless of how they were structured (e.g., whether trends were identified, data entry errors corrected, or other preprocessing steps applied) – the key statistical characteristics of the acceptance parameters were calculated. the analysis revealed a substantial spread in mechanical property values (Tables 1 and 2).

The greatest variability in property values was observed for impact strength, compared to strength parameters. For example, in 13G1S-U steel, the maximum toughness value exceeded the minimum by a factor of 5 – 6, while for 38KhN3MFA-Sh steel, the difference was twofold – similar trends were also observed in other types of metal products [10]. Such heterogeneity in toughness is attributed to differences in the scenarios of technological inheritance – the realization of diverse mechanisms of structural and defect evolution along the technological chain, ultimately leading to a wide variety of morphologies in nominally similar final structures [1; 16; 17]. This underscores the need for an objective assessment of the extent of variability in impact strength. Consequently, any variation in the number of tested samples (in this case, per individual forging or sheet batch) can become a significant factor affecting the reliabil.

However, comparing different datasets solely based on their mean values and ranges does not always provide a complete picture of the variability in the quality characteristics of metal products. However, comparing different datasets solely based on their mean values and ranges does not always provide a complete picture of the variability in the quality characteristics of metal products. For instance, a large range may result from the presence of isolated outliers, and mean values and their variances are meaningful only if the distribution of quality parameters approximates a normal pattern [10]. This consideration motivated the construction of distribution histograms. Separate histograms were constructed for the results of the first {\(KCU_i^{ - 40}\)}, second {\(KCU_j^{ - 40}\)}, and third {\(KCU_k^{ - 40}\)} tests for 13G1S-U steel, and for the first {\(KCU_i^{ - 50}\)} and second {\(KCU_j^{ - 50}\)} tests for 38KhN3MFA-Sh steel, with the test number corresponding to a specific column in the data matrix (Fig. 2).

The distribution of impact strength values showed noticeable deviations from the normal distribution. the extent of this deviation was assessed based on the corresponding skewness and kurtosis coefficients, which varied over a fairly wide range. For 38KhN3MFA-Sh steel, the skewness (A_s) and kurtosis (E_x) coefficients of impact strength values ranged from \(\left[ {-0.43;-0.31} \right]\) and \(\left[ {0.70;0.80} \right]\), respectively for templates with diameter D_s and within \(\left[ {-0.31;0.35} \right]\) and \(\left[ {-0.14;0.23} \right]\) for templates with diameter D_l . For the distributions of KCV⁰ and KCU^–40 impact strength values in 13G1S-U steel – specifically for sheets with a thickness of 8 mm – the skewness and kurtosis coefficients ranged as follows: \(\left[ {1.64;1.68} \right]\); \(\left[ {1.54;1.81} \right]\) and \(\left[ {3.12;3.40} \right]\); \(\left[ {3.40;5.29} \right]\). Differences in the statistical indicators derived from individual test results – {\(KCU_i^{ - 40}\)}, {\(KCU_k^{ - 40}\)}, {\(KCU_i^{ - 40}\)} and {\(KCV_i^0\)}, {\(KCV_j^0\)}, {\(KCV_k^0\)} (assuming that impact strength was assessed using only one sample per product unit – either a sheet batch or a forging) – reflect underlying differences in the statistical nature of these datasets. the absolute values of the skewness and kurtosis coefficients provide a quantitative measure of deviation from a normal distribution. This, in turn, underscores the need to account for the shape of the distribution when determining the appropriate number of samples required for metal product certification.

In statistical analysis, the reliability of results depends heavily on the sample size [1; 13]. For samples with the largest available volumes (V_i), the error in calculating the skewness and kurtosis coefficients was minimal – 0.23 and 0.77, respectively. As the sample size V_i decreased – starting from V_i = 200 – 250 for sheet steel (depending on thickness) and V_i = 150 – 200 for forgings – both the variability in skewness values and the associated estimation error increased noticeably. With further reductions in sample size – for example, in the case of KCU^–40 impact strength values (based on three samples per batch) for 13G1S-U steel sheets 12 mm thick – the skewness coefficient (A_s), calculated across 20 subsamples (each containing 50 batches) sequentially extracted from an original dataset of 1000 batches, ranged within \(\left[ {-0.2;2.2} \right]\), with an estimation error of 3.0. Clearly, at this level of variation of coefficient A_s and with such a high error margin, the resulting statistical estimates cannot be considered reliable. the same conclusion applies to impact strength samples for 38KhN3MFA-Sh steel forgings.

In this context, relying on mean values across samples and applying classical statistical tests for comparison may introduce uncertainty into the resulting assessments. For example, pairwise comparisons of impact strength values in 13G1S-U steel – based on the standard testing results from three samples per batch (Table 3) – revealed that the significance level of the hypothesis of sample equivalence differed considerably when evaluated using the Student’s and Smirnov tests [18], with discrepancies reaching up to 30 %. In practical terms, this means that the three possible pairwise combinations of impact strength results from each batch (i.e., product unit) may follow different distribution patterns, suggesting differences in their underlying statistical nature. As a result, classical statistical criteria such as the Student’s test may not always confirm the equivalence of samples – and in some cases, simultaneous use of the Student’s and Smirnov’s tests may even lead to contradictory conclusions.

It is clear that testing two samples per product unit improves the overall completeness of the quality assessment, compared to testing just one. However, this also raises the question of how to select a single value that adequately represents the product’s quality. Calculating the mean \({\bar X_i}\) of two values may be inappropriate, as the same average can correspond to different ranges (Δ) between maximum and minimum values. Likewise, samples with identical ranges may differ in their absolute property levels, such as the median. One possible approach to statistical analysis is to select the minimum (i.e., worst-case) toughness value; however, it is generally preferable to base such decisions based on a comprehensive evaluation of all possible assessment options [19].

From a general standpoint, it is evident that testing three samples per product unit not only allows for estimating the standard error of the mean (s), but also provides a more objective assessment of quality heterogeneity – both in terms of standard deviation and range (Δ).

Distributions of impact strength ranges (ΔKCU^–40) were constructed based on the results of all three tests conducted for each batch of 13G1S-U steel sheets (12 mm thick), as well as on all possible pairwise combinations of these results (Δ_i–j, Δ_i–k and Δ_j–k, where indices correspond to column numbers in the data matrix). A unified binning method was used to make these distributions comparable (Fig. 3).

All resulting histograms of range values exhibited right-skewed distributions, as confirmed by the calculated skewness (A_s) and kurtosis (E_x) coefficients (Table 4).

As expected, the absolute skewness and kurtosis values for the full three-sample distributions (Δ = KCU_max – KCU_min) оwere lower than those for the pairwise combinations. However, the absolute ranges based on three samples exceeded the pairwise ranges (Δ_i – j, Δ_i – k and Δ_j – k) in 56.4 – 67.7 % of cases across all sheet thicknesses and batches. In the pairwise data, range values tended to be smaller: the majority fell into the first bin, some were identical (zero range), and in subsequent bins, the number of values was 1.5 to 2.5 times lower than in the histogram based on three-sample data. All pairwise range datasets of range values (Δ_i – j, Δ_i – k and Δ_j – k) for KCU^–40 and KCV⁰ impact strength of 13G1S-U steel sheets 8, 10, and 12 mm thick) differed significantly from the original distribution: the experimental values of the Student’s and Smirnov’s test statistics were no less than 4.61 and 2.77, respectively (with a significance level of p < 0.0001).

However, when testing the significance of differences between the pairwise range distributions for KCU^–40 and KCV⁰, full consistency between the two statistical tests was no longer observed. In 9 out of the 18 possible pairwise comparisons (i.e., three combinations – Δ_i – j, Δ_i – k and Δ_j – k – for each of the three sheet thicknesses: 8, 10, and 12 mm, and for both types of impact strength: KCU^–40 and KCV⁰ for 13G1S-U steel), the risk levels for the hypothesis of sample difference varied between 0.22 and 0.50. Statistical equivalence was confirmed in these 9 comparisons; in the remaining 9, the samples were found to differ in 6 and 3 cases at risk levels not exceeding 0.20 and 0.30, respectively (according to at least one of the two tests), regardless of sheet thickness or type of impact strength.

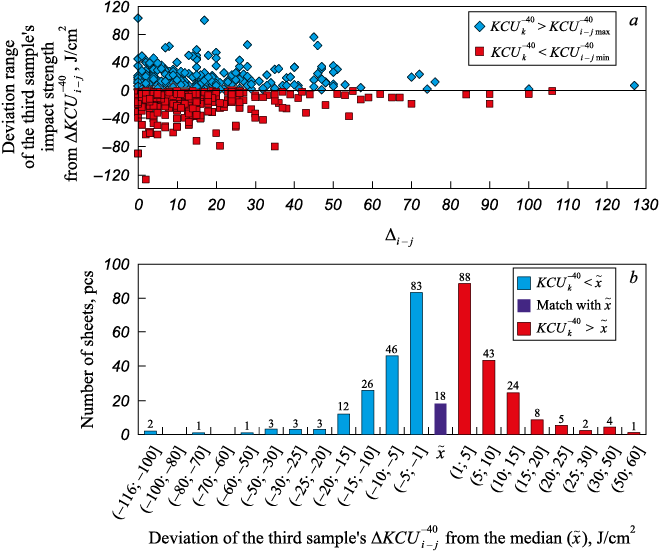
Relative to the impact strength values initially obtained from two samples, the value from the third sample may occupy a different position along the corresponding impact strength axis – not only to the left or right of the minimum and maximum values, respectively, but also between them (if they are not equal), for example, to the left or right of the median value calculated from the initial pair of test results).

The positional statistics of the impact strength values of the third sample \(KCU_k^{ - 40}\) (relative to the corresponding values of the sample pairs \(KCU_i^{ - 40}\) and \(KCU_j^{ - 40}\)) exhibited a fairly typical pattern. For example, in the case of 13G1S-U steel sheets 12 mm thick, the proportion of \(KCU_k^{ - 40}\) values falling below and above the limits of the impact strength interval defined by individual sample pairs [\(KCU_i^{ - 40}\); \(KCU_j^{ - 40}\)] was approximately the same (Fig. 4, a). It is evident that even a slight deviation beyond the interval boundaries can significantly affect the median-based statistics when they are transformed into mean values – either upward or downward. When these deviations are more substantial, their influence becomes even more pronounced. the third sample’s value fell within the pairwise impact strength interval [\(KCU_i^{ - 40}\); \(KCU_j^{ - 40}\)] in 373 to 402 cases (36.5 – 39.4 % of all batches); of these, 180 to 184 values were lower than the corresponding median values \({\tilde x_i} = \frac{{KCU_i^{ - 40} + KCU_j^{ - 40}}}{2},\) and 175 to 202 were higher (Fig. 4, b). Exact matches with the median values were observed in only 1.6 to 1.8 % of cases, effectively converting the median into the batch mean. All other values, to varying degrees, influenced the batch-level impact strength estimate. This highlights the potential risks when reversing the process – i.e., reducing the number of samples used to assess batch impact strength from three to two.

However, in steels with pronounced structural heterogeneity, even testing three samples may not guarantee objective quality assessments – particularly with regard to impact strength. This is especially true for steels retaining cast structure (e.g., large forgings made of heat-treatable steel such as 38KhN3MFA-Sh or 15Kh2NMFA) and for high-strength rolled steels with ferrite–pearlite or ferrite–bainite banded microstructures [7; 20 – 22]. The presence of pronounced morphological heterogeneity – including non-metallic inclusions (NMIs) – both between samples and within individual samples, leads to a wide spread of impact strength values across the full range of test temperatures. This introduces uncertainty in the evaluation of toughness, including the determination of cold resistance.

In this context, the use of micro-samples appears promising: if their dimensions are comparable to the scale of structural heterogeneity, it becomes possible to evaluate the cold resistance of individual structural components and rank them by associated fracture risk, based on brittle fracture energy determined through acoustic emission measurements [7]. This is important for understanding the causes of toughness variability observed under standard testing protocols. It was precisely this approach that demonstrated that in large forgings of 38KhN3MFA-Sh heat-treatable steel, brittle fracture within the –130 to 100 °C range occurs only in the interdendritic regions, whereas below –130 °C, the dendrite axes themselves also undergo brittle fracture. Variations in dendritic structure patterns from one impact sample to another – including their downstream effects on microstructure and the morphology of non-metallic inclusions (NMIs) [1] – lead to increased scatter in toughness values at all test temperatures and reduce the reliability of cold resistance predictions.

For 15Kh2NМFA steel, such tests have made it possible to clarify the temperature range of the ductile-to-brittle transition and relate it to the fracture mechanism (transcrystalline, intergranular, or mixed). This is crucial for assessing potential cold resistance degradation during long-term operation when the number of witness samples is limited, as well as under conditions with a small number of samples available during acceptance testing.

The use of this approach proved valuable not only for evaluating the cold resistance of structural components but also for assessing the risk associated with structural anomalies. For instance, in high-strength pipe steels of strength grade K65, micromechanical testing made it possible to localize fracture within an extended interface region of the metal, accompanied by the formation of large facets approximately 500 μm in diameter each. This was identified as one of the possible causes of delamination (slate fracture appearance [20]), and the fracture energy was evaluated based on acoustic emission measurements [7].

Overall, the findings indicate that several factors – such as the varying statistical nature of property distributions in acceptance test results (particularly within the examined chronological sequences), differences in the extent to which property variability is captured depending on the number of samples tested per product unit, the potential for conflicting outcomes in hypothesis testing depending on the statistical criteria applied, and the diversity of mechanisms of technological inheritance embedded in standard production processes (many of which remain insufficiently studied) [1; 7] – will inevitably and substantially constrain the effective application of modern software solutions in the development of end-to-end quality management systems for metal production.

Advancement in this field must be based on a deep understanding of structural and defect evolution throughout the entire technological chain, as well as the development of digital tools for quantitative analysis of microstructures and fracture surfaces, with their integration into industrial practice to enhance the completeness of product quality certification. It also requires the application of statistical procedures that take into account the statistical characteristics of the material under investigation, the identification of domains governed by dominant types of dependency (within the technological parameter space), and the evaluation of their combined effects [7; 15; 19].

Conclusions

Based on statistical analysis of representative production control datasets for the manufacturing processes of 13G1S-U steel sheets (8, 10, and 12 mm thick) and large forgings made from heat-treatable 38KhN3MFA-Sh steel, several factors have been identified that account for discrepancies in quality assessment outcomes during acceptance testing when different numbers of samples are used per product unit (batch or forging). These factors include: variation in the recorded property range (i.e., the spread of values); changes in the statistical characteristics of property value distributions (as reflected by variations skewness and kurtosis coefficients); and the size of the analyzed dataset.

It has been shown that, in the statistical analysis of production control databases, proper data preprocessing plays an important role in eliminating side effects that reduce the informativeness of acceptance testing results. Such preprocessing should aim to remove the influence of trends, seasonal fluctuations, outliers, and similar factors.

It was found that reducing the number of samples per batch from three to two in the acceptance testing of 13G1S-U steel sheets results in a 17 – 20 % increase in the frequency of minimum impact strength range (Δ) values (0 to 34 J/cm²) and a 2.0 – 3.5-fold decrease in the number of ranges within the 35 to 136 J/cm² interval. This leads to a distorted assessment of toughness heterogeneity in the steel. For 38KhN3MFA-Sh steel, even greater distortions can be expected due to the pronounced heterogeneity in structural morphology (including dendritic patterns, microstructural features, and nonmetallic inclusions).

When the number of tests per product unit varies – resulting in changes in the distribution pattern of quality indicators within the sample as a whole – the application of statistical hypothesis testing (e.g., the Student’s and Smirnov’s tests) may yield inconsistent results across different sample sets. This factor should be carefully considered when using modern software tools (such as big data analytics, machine learning, and related technologies) for retrospective analysis of production control databases in metallurgy.