Перейти к:
Комплексная энергодинамическая модель конвертерной плавки
https://doi.org/10.17073/0368-0797-2025-3-209-217
Аннотация
На практике для описания кислородно-конвертерного процесса широко используются так называемые статические модели, описывающие изменения выходных параметров на основе информации о входных параметрах для каждого отдельного цикла производства (плавки). Дополнительно используемые модели заключительного периода позволяют обеспечить более точное попадание в заданные пределы по температуре и содержанию углерода в металле. При этом в качестве исходной используется информация о результатах промежуточного замера параметров металла фурмой-зондом, который проводится в период расхода 80 – 95 % общего кислорода на плавку. Для описания поведения объекта по ходу процесса от начала и до конца производственного цикла необходимо построение модели, основанной на закономерностях взаимодействия фаз в открытой системе (кислородном конвертере). В настоящей работе предпринята попытка построения такой модели с использованием концепции стационарного неравновесного состояния и результатов физического и математического моделирования системы при изменении величины площади контакта двух несмешивающихся жидкостей при воздействии на них струи газа. При формировании модели исходили из наличия в расплаве двух основных реакционных зон окисления компонентов, которые в соответствии с современными представлениями определяют механизм процессов и гидродинамику расплава при продувке конвертерной ванны. Для каждой выделенной зоны в значительной степени характеристики массопереноса в различные периоды операции в зависимости от текущих параметров взаимодействующих фаз определяют скорости химических реакций. Результаты проверки адекватности модели с использованием практических данных позволяют заключить, что модель может быть использована для исследования процесса продувки в кислородном конвертере.
Ключевые слова
Для цитирования:
Шакиров М.К., Протопопов Е.В., Турчанинов Е.Б., Беленецкий Е.А., Фатьянов С.С. Комплексная энергодинамическая модель конвертерной плавки. Известия высших учебных заведений. Черная Металлургия. 2025;68(3):209-217. https://doi.org/10.17073/0368-0797-2025-3-209-217
For citation:
Shakirov M.K., Protopopov E.V., Turchaninov E.B., Belenetskii E.A., Fat’yanov S.S. Complex energy-dynamic model of BOF melting. Izvestiya. Ferrous Metallurgy. 2025;68(3):209-217. https://doi.org/10.17073/0368-0797-2025-3-209-217
Введение
Комплексное описание процессов, протекающих в кислородном конвертере, является сложной многофакторной задачей. На практике для управления конвертерной плавкой с целью достижения заданных значений параметров полупродукта широкое распространение получили так называемые статические модели и модели заключительного периода. Статические модели [1 – 3] основываются на информации о свойствах использующихся материалов и требуемых значениях показателей полупродукта по окончании операции продувки и предназначены, в основном, для предварительного определения расходов компонентов металлозавалки (металлического лома, жидкого чугуна), добавочных материалов (извести, охладителей магнезиальных флюсов и т. д.) и кислорода на плавку. Для такого описания циклического процесса выплавки стали, как правило, используются модели теоретические [4 – 6] и статистические [7 – 9]. Модели заключительного периода используют результаты промежуточного замера параметров хода операции фурмой-зондом и служат для корректировки предварительно фиксированных количеств материалов и кислорода с целью определения момента окончания продувки [10 – 12]. Однако такие модели не позволяют получать информацию о параметрах процесса по ходу продувки, что может вносить определенные сложности при использовании новых материалов и элементов технологии, а также для совершенствования режимов ведения плавки и показателей процесса.
Постановка задачи и формирование обобщенной модели
С целью описания процессов, происходящих в конвертере, в том числе влияния различных параметров на ход и показатели окончания операции, была сформулирована задача: разработать обобщенную модель, базирующуюся на физико-химических представлениях о закономерностях взаимодействия фаз в конвертерном агрегате. В основу легли концепция стационарного неравновесного состояния (СНС) [13] и предложенный в работе [14] подход, связанный с термином «энергодинамика». В развитии известных работ [13 – 15] для оценки величины поверхности контакта взаимодействующих фаз и показателей скорости протекания гетерогенных реакций предполагалось использование информации, накопленной при выполнении физического и математического моделирования [16 – 19].
Для описания процесса на первом этапе выделили элементы системы или взаимодействующие фазы, характеризующиеся собственными физико-химическими свойствами, при этом между фазами происходит активное взаимодействие. Именно поэтому для описания процесса необходима оценка связанных между собой показателей, описывающих состояние и взаимодействие фаз по ходу операции.
Выплавка полупродукта в конвертере характеризуется непрерывным изменением условий протекания химических реакций:
– изменение количеств взаимодействующих фаз:
• жидкие металлическая (рафинируемый металл) и оксидная (шлак);
• твердые металлическая (лом) и оксидная (флюсы, охладители, неметаллическая составляющая твердой металлозавалки);
• газообразная, содержащаяся в шлакометаллической эмульсии в виде пузырей СО и всплывающих макрообъемов отходящих газов;
– изменение химического состава взаимодействующих фаз:
• жидкая металлическая ванна (рафинируемый металл);
• жидкая оксидная фаза (шлак);
• газообразная (всплывающие пузыри газа);
– изменение температуры взаимодействующих фаз;
– изменение параметров продувки: скорости подачи кислорода и положения фурмы относительно уровня металлической ванны в соответствии с используемыми режимами продувки;
– изменение геометрических параметров рабочего пространства вследствие износа огнеупорной футеровки по ходу кампании конвертера.
Количество взаимодействующих фаз
Изменение количеств фаз, взаимодействующих в конвертере, происходит вследствие протекания следующих процессов:
– шихтовки плавки: завалки лома и заливки чугуна, включая возможное наличие металла и шлака предыдущей плавки (в том числе шлака, нанесенного на футеровку агрегата в виде гарнисажа различными способами); присадки добавочных материалов (флюсы, охладители, твердое и газообразное топливо) до начала и по ходу продувки;
– фазовых переходов: расплавления и растворения твердых компонентов металлозавалки, флюсов и охладителей в жидких металлической и оксидной фазах, а также обратных процессов; износа рабочего слоя огнеупорной футеровки;
– протекания реакций окисления железа и примесей металлической ванны при взаимодействии с кислородными струями;
– протекания окислительно-восстановительных реакций и реакций диссоциации на поверхности раздела фаз.
В общем виде изменение количества f-й фазы в течение любого периода продувки можно описать следующим выражением:
| \[w_f^t = w_f^{t - 1} + \sum\limits_{g = 1}^G {\Delta {w_{gf}}} + \sum\limits_{h = 1}^H {\Delta {w_{hf}}} + \sum\limits_{i = 1}^I {\Delta {w_{if}}} + \sum\limits_{j = 1}^J {\Delta {w_{jf}}} ,\] | (1) |
где \(w_f^t\) и \(w_f^{t - 1}\)– количество f-ой фазы по окончании текущего периода и по окончании предшествующего периода продувки; ∆wgf – изменение количества f-ой фазы в результате загрузки/присадки в конвертер g-го материала, не образующего отдельную фазу; ∆whf – изменение количества f-ой фазы в результате фазового перехода фазы h в фазу f либо обратного процесса; ∆wif – изменение количества f-ой фазы за счет изменения количеств реагентов, а также продуктов в результате протекания i-ой реакции окисления газообразным кислородом; ∆wjf – изменение количества f-ой фазы за счет изменения количеств реагентов, а также продуктов в результате протекания j-ой окислительно-восстановительной реакции на поверхности раздела шлак – металл.
Твердая металлическая фаза представляет собой смесь компонентов металлозавалки с возможным образованием на начальных этапах операции конгломератов и «намораживанием» на поверхности фрагментов твердой металлозавалки. Твердая оксидная фаза представляет собой смесь различных добавочных материалов, не перешедших на текущий момент в жидкую или газообразную фазы (флюсы, охладители, неметаллическая часть твердой металлозавалки, шлак предыдущей плавки).
Таким образом, отдельные составляющие металлической и оксидной фаз характеризуются собственным химическим составом и физическими свойствами, определяющими особенности взаимодействия и скорость перехода в жидкую фазу.
Химический состав взаимодействующих фаз
Изменение химического состава взаимодействующих фаз происходит в результате протекания тех же процессов, которые обуславливают изменение количеств взаимодействующих фаз.
В общем виде изменение содержания элемента (оксида) X в фазе f в течение любого периода продувки можно описать следующим выражением:
| \[[X]_f^t = \frac{{[X]_f^{t - 1}w_f^{t - 1} + \sum\limits_{p = 1}^P {\Delta {w_{Xp}}} }}{{w_f^t}},\] | (2) |
где \([X]_f^t\) и \([X]_f^{t - 1}\) – содержание элемента (оксида) X фазы f по окончании текущего периода и по окончании предшествующего периода продувки; p – номер стадии процесса (присадка материала, фазовый переход, окисление в первичной зоне, окисление/восстановление на поверхности раздела шлак – металл); ∆wXp – изменение количества элемента (оксида) X в составе фазы f в результате протекания процесса p в текущий период продувки.
Температура взаимодействующих фаз
Изменение температуры взаимодействующих фаз происходит в результате протекания следующих процессов:
– теплообмен между фазами, состояние которых характеризуется текущими значениями их теплофизических свойств (температура, теплоемкость, количество);
– протекание реакций окисления (железа и примесей), восстановления (оксидов железа, марганца и фосфора), диссоциации (гидроксидов, карбонатов) с выделением или поглощением тепла;
– фазовые переходы (характеризуются энтальпией фазового перехода);
– обмен энергией с окружающей средой (потери тепла через футеровку, излучением и с отходящими газами).
Для определения изменения температуры взаимодействующих фаз в течение любого периода продувки использовали следующее выражение:
| \[\begin{array}{c}{T^t} = {T^{t - 1}} + \\ + \frac{{\sum\limits_{a = 1}^A {{H_a}w_a^t} - \sum\limits_{i = 1}^I {\Delta {H_i}\Delta w_{ir}^t} - \sum\limits_{h = 1}^H {\Delta {H_h}\Delta w_h^t} - \sum\limits_{l = 1}^L {{H_l}w_l^t} }}{{\sum\limits_{f = 1}^F {C_{pf}^tw_f^t} }},\end{array}\] | (3) |
где Ha и \(w_a^t\) – удельная энтальпия и количество материала а, присаженного в конвертер в текущий период t продувки; ∆Hi и ∆\(w_{ir}^t\) – энтальпия i-ой реакции, приведенная к единице количества реагента r, и изменение количества реагента r в текущий период t; ∆Hh и ∆\(w_h^t\) – энтальпия фазового перехода, приведенная к единице количества фазы, претерпевающей фазовый переход h, и количество фазы, претерпевающей фазовый переход в текущий период t; Hl и \(w_l^t\) – удельная энтальпия и количество газа l, покидающего конвертер в составе отходящих газов в текущий период t; \(C_{pf}^t\) и \({w_f^t}\) – удельная теплоемкость при постоянном давлении и количество конденсированной фазы f на момент окончания текущего периода t.
Удельные энтальпии веществ и энтальпии реакций определяются с использованием стандартных величин и температурных зависимостей удельной теплоемкости индивидуальных веществ.
Параметры дутьевого режима
Изменения параметров продувки кислородом обусловлены задачами, решаемыми на различных этапах:
– интенсивное шлакообразование на начальных стадиях продувки;
– поддержание динамического равновесия процесса окисления железа (примесей) и процесса окисления углерода в период интенсивного обезуглероживания;
– обеспечение получения химического состава металла в заданных пределах в заключительный период продувки.
Условия взаимодействия фаз изменяются в зависимости от параметров продувки (интенсивность, положение фурмы над уровнем ванны), а также температуры, количеств металла, шлака и геометрических характеристик рабочего пространства.
Скорость протекания химических реакций
и площадь контакта взаимодействующих фаз
Скорость протекания химических реакций определяется текущими параметрами:
– фазовым составом системы;
– температурой;
– текущим содержанием исходных компонентов и продуктов реакций во взаимодействующих фазах;
– содержанием исходных компонентов и продуктов реакций во взаимодействующих фазах в стационарном неравновесном состоянии.
Концентрации компонентов шлака и металла определяли как их содержание, соответственно, в жидкой оксидной и жидкой металлической фазах. Полагали, что протекание химических реакций возможно с участием только жидких и газообразных фаз. При этом количества и концентрации компонентов жидких фаз в каждом периоде расчета могут изменяться, в том числе за счет фазовых переходов.
Общее количество шлака определялось как сумма количеств твердой и жидкой оксидных фаз, металла – как сумма количеств твердой и жидкой металлических фаз.
Известно, что кинетическое уравнение химической реакции в общем виде может быть представлено как
| V0 = kv Am Bn , | (4) |
где kv – константа скорости реакции, является функцией температуры и не зависит от концентраций реагирующих веществ; A, B – концентрации реагентов; m и n – порядок реакции по реагентам A и B соответственно.
Кинетическое уравнение гетерогенной реакции описывает скорость, соответствующую количеству элементарных актов взаимодействия, происходящих в единицу времени на единице поверхности раздела фаз.
В соответствии с изложенным, для расчета значений ∆wif , ∆wjf из зависимости (1) и ∆wXp из зависимости (2) необходимо оценить площадь контакта взаимодействующих фаз.
Известно [3; 14], что реакции окисления протекают на поверхности контакта взаимодействующих фаз в реакционных зонах расплава при продувке:
– первичная зона – зона контакта кислородных струй с жидкой металлической ванной;
– вторичная зона – в общем виде зона контакта газовой и жидких металлической и оксидной фаз.
Скорость окисления примесного элемента определяли как сумму скоростей соответствующих реакций в первичной и вторичной зонах.
Первичная реакционная зона. Это зона непосредственного усвоения кислорода дутья. Для первичной зоны полагали протекающими в кинетическом режиме реакции окисления кремния, марганца и фосфора, а также углерода при его концентрациях выше переходной и критической. Приняли первый порядок реакций окисления, содержание кислорода в газовой фазе при контакте с жидким металлом постоянным и равным единице. При этих условиях скорость окисления примеси X можно определять в соответствии со следующим выражением:
| V1X = kv S1[X], | (5) |
где kv – константа скорости реакции; S1 – текущая величина площади контакта кислородных струй с жидким металлом; [X] – текущее содержание окисляемого элемента в жидком металле.
Скорость окисления углерода в области низких (ниже критической) концентраций, когда процесс лимитируется массопереносом углерода к месту протекания реакции (диффузионный режим), можно определять как
| V1C = km S1([C] – [C]*), | (6) |
где km – коэффициент массопереноса углерода в жидком металле; [C] – текущая концентрация углерода в расплаве; [C]* – предельно достижимое содержание углерода, являющееся функцией характеристик продувочных устройств и геометрических параметров рабочего пространства конвертера.
Вторичная реакционная зона. Для реакций окисления кремния, марганца, фосфора и углерода в области более низких концентраций основным является диффузионный режим протекания, а для описания скорости соответствующих процессов c учетом величины площади контакта взаимодействующих фаз можно использовать кинетические уравнения типа [20]:
| V2X = km S2([X] – [X]*), | (7) |
где km – коэффициент массопереноса; S2 – текущая величина площади контакта взаимодействующих конденсированных фаз; [X] и [X]* – текущее и равновесное содержания элемента в жидком металле (для углерода – предельно достижимое содержание).
Величину равновесного содержания элемента в жидком металле можно определить в соответствии с известной температурной зависимостью константы равновесия соответствующей реакции:
| \[\ln K = \frac{a}{T} + b,\] | (8) |
где K – константа равновесия химической реакции; Т – текущая температура; a, b – константы.
Поскольку константа равновесия химической реакции определяется отношением произведения концентраций продуктов реакции к произведению концентраций реагентов для состояния равновесия, увеличение в шлаке содержания продуктов окисления приводит при прочих равных к увеличению значения [X]* и изменению скорости реакции в сторону отрицательных значений, то есть преимущественному развитию обратной реакции в соответствии с зависимостью (7). Увеличение содержания реагентов есть увеличение текущего значения [X], при этом будет происходить увеличение скорости протекания реакции в прямом направлении.
Для описания скорости реакции окисления углерода во вторичной зоне в области так называемых переходных концентраций использовали кинетическое уравнение типа [21; 22]:
| V2C = kv S2[C]m (FeO)n, | (9) |
где (FeO) – содержание оксидов железа в шлаке.
Величины kv и km констант скорости и коэффициентов массопереноса в уравнениях (5) – (7), (9) можно аппроксимировать линейными температурными зависимостями.
Определение площади контакта
взаимодействующих фаз
Площадь контакта кислородных струй с жидким металлом по ходу продувки аппроксимировали величиной, прямо пропорциональной динамическому напору струи кислорода на срезе сопла и обратно пропорциональной квадрату высоты фурмы над уровнем металла, аналогично полученным ранее данным для оценки заглубления струй газа в жидкую ванну [14].
Методами физического и математического моделирования получена информация [16 – 18] о влиянии различных параметров на величину площади контакта металлической и шлаковой фаз.
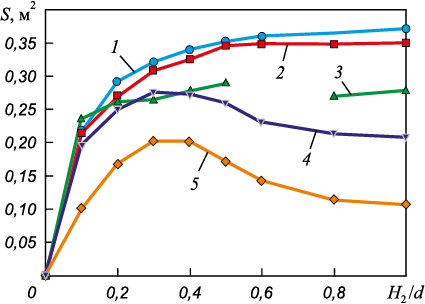
В качестве характерного примера (рис. 1 и 2) [18] представлены результаты низкотемпературного моделирования взаимодействия металлической и шлаковой фаз при продувке газовыми струями. По результатам моделирования, например, выявлено влияние на площадь контакта S фаз таких параметров, как высота фурмы (hф ), скорость подачи газа (q) и количество шлака (h2 ).
Рис. 1. Влияние высоты слоя шлака H2 , отнесенной к диаметру реактора d,
Рис. 2. Влияние высоты слоя шлака H2 , отнесенной к диаметру реактора d, |
При построении математического описания, очевидно, необходимо учитывать особенности влияния относительного количества шлака в конвертерной ванне по ходу продувки, такой параметр может быть учтен как
| \[{H_2} = \frac{{{h_2}}}{{{d_{\rm{p}}}}},\] | (10) |
где dр – диаметр модели.
Неоднозначный характер зависимости величины межфазной поверхности S от общего количества шлака может быть объяснен различным влиянием параметра H2 /d на скорость (vs ) образования капель металла (корольков в шлаке – элементов дополнительной межфазной поверхности) и продолжительность их существования по ходу плавки (τs ):
| S = vs τs , | (11) |
При этом время существования капель и корольков металла в шлаке будет определяться свойствами жидкости, параметрами струи газа, размерами основного циркуляционного контура движения расплава и капель (корольков) в шлаке, скорость образования дополнительной поверхности – параметрами продувки и высотой слоя менее плотного вспененного шлака [18].
Дожигание отходящих газов
Количество углерода, окисляющегося до CO и СО2 , целесообразно определять в соответствии с уравнением температурной константы равновесия реакции окисления оксида углерода CO газообразным кислородом
| 2CO + O2 = 2CO2 . | (12) |
В данном случае принимается, что скорость реакции в газовой фазе высока и равновесие достигается в текущем периоде продувки при любой выбранной для расчета его продолжительности.
Окисление железа
В соответствии со стехиометрическими отношениями для каждой реакции окисления, протекающей в текущий период расчета в первичной и вторичной реакционных зонах, а также с учетом протекания реакции дожигания оксида углерода CO определяли требуемое количество кислорода.
Для определения расчетного количества кислорода на окисление железа в текущем периоде из общего количества кислорода, поступающего в ванну в соответствии с параметрами дутьевого режима, вычитали количество кислорода для окисления примесных элементов расплава и для дожигания оксида углерода CO:
| \[q_{{{\rm{O}}_2}}^{{\rm{Fe}}} = {q_{{{\rm{O}}_2}}} - \sum\limits_{i = 1}^N {q_{{{\rm{O}}_2}}^{{X_i}}} ,\] | (13) |
где \({q_{{{\rm{O}}_2}}}\) – количество кислорода, поступающее в ванну с дутьем в течение текущего периода; \(q_{{{\rm{O}}_2}}^{{X_i}}\) – количество кислорода, израсходованного на окисление i-го элемента или оксида углерода CO.
Далее рассчитывали количество окислившегося за соответствующий период железа и образующегося оксида железа по стехиометрическим соотношениям.
Для каждой протекающей реакции (помимо количества прореагировавших компонентов и образовавшихся продуктов) определяли соответствующий этим количествам тепловой эффект. Энтальпию отходящих газов для расчета потерь тепла (3) рассчитывали как функцию теплоемкости и температуры газа, принятой равной текущей температуре конденсированных фаз.
Скорость протекания реакций, определенную с учетом площади поверхности контакта взаимодействующих фаз, использовали для расчетов в соответствии с выражениями (1) – (3).
Скорость плавления/растворения материалов в расплаве
Массовую скорость растворения/плавления каждого добавочного материала и металлического лома по ходу продувки возможно определять по эмпирическим выражениям как линейную функцию его текущего количества в твердом состоянии и средней температуры конденсированных фаз на момент начала текущего периода. Например, для легковесного металлического лома коэффициенты уравнения скорости плавления настраивались таким образом, чтобы по результатам расчета плавки их переход в жидкую фазу завершался уже к 20 – 30 %, а для тяжеловесного лома к 50 – 80 % продолжительности продувки.
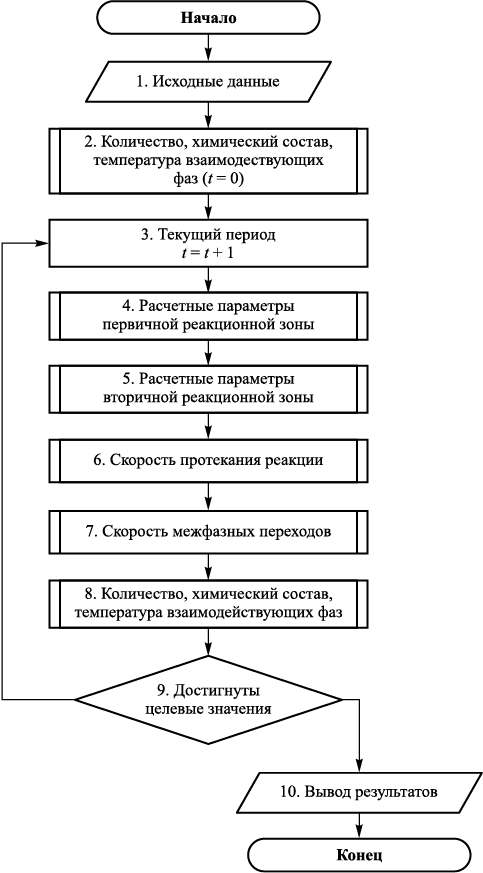
Таким образом, функционирование модели подразумевает определение текущих значений количества, химического состава и температуры взаимодействующих фаз на момент окончания каждого условного периода продувки. В дальнейшем полученные значения используются в качестве исходных для расчета последующего периода. Например, для практического применения при реализации расчета выбирается продолжительность условного периода, соответствующая 200 м3 израсходованного кислорода. Укрупненный алгоритм функционирования модели представлен на рис. 3.
Рис. 3. Укрупненный алгоритм функционирования модели |
Таким образом, минимальный объем исходных данных для расчетов должен включать в себя следующую информацию:
– химический состав и количества шихтовых материалов (жидкого чугуна, характеристики металлозавалки), а также добавочных материалов (флюсов, охладителей);
– температуру жидкого чугуна;
– предварительно заданные или фактические параметры дутьевого режима (положение фурмы, расход кислорода и т. д.) и шлакового режима (режима присадок материалов по ходу продувки);
– целевые или фактические показатели окончания продувки: температуру металла, содержания углерода, марганца, серы и фосфора в металле по окончании продувки.
Результаты исследования и их обсуждение
Как результат реализации такого алгоритма решения комплексной задачи получены расчетные значения температуры, химического состава металла по окончании продувки, расхода кислорода на плавку, а также траектории изменения значений этих параметров и параметров шлаковой фазы по ходу операции.
Проверку адекватности модели осуществляли по данным 200 плавок текущего производства, проведенных в 350-т конвертере при использовании дополнительного контроля показателей процесса фурмой-зондом. Использовали фактическую информацию: количество, режимы присадок материалов, режимы продувки, количество израсходованного кислорода, химический состав металла по окончании продувки. Остановку расчетов модели проводили по достижении содержания углерода в металле, равного фактически полученному на моделируемой плавке. Настройка коэффициентов модели позволила получить следующие результаты: диапазоны изменения (числитель) и средние значения (знаменатель) параметров окончания продувки (табл. 1).
Таблица 1. Параметры окончания продувки
|
Ошибки ∆ расчета показателей окончания продувки определяли как разность фактических и расчетных значений. В табл. 2 приведены значения средних (числитель) и средних по модулю (знаменатель) значений ошибок расчета.
Таблица 2. Ошибки прогноза параметров
|
Выводы
Достигнутые значения ошибок расчета показателей окончания продувки конвертерной ванны позволяют говорить об адекватности модели, разработанной в соответствии с описанным подходом. В свою очередь это позволяет сделать заключение о возможности использования модели для оценки влияния изменений состава, количества, свойств используемых материалов, технологических режимов и параметров рабочего пространства агрегата на динамику изменения параметров взаимодействующих фаз и показатели окончания продувки в кислородном конвертере, что поможет снизить количество корректирующих операций.
Список литературы
1. Туркенич Д.И. Управление плавкой стали в конвертере. Москва: Металлургия; 1971:360.
2. Бойченко Б.М., Низяев К.Г., Стоянов А.Н., Молчанов Л.С., Синегин Е.В. Параметризация процесса выплавки стали в кислородном конвертере. Системные технологии. 2017;(3(110)):10–15.
3. Бигеев A.M. Математическое описание и расчеты сталеплавильных процессов. Москва: Металлургия; 1982:160.
4. Мочалов С.П., Айзатулов Р.С., Шакиров К.М. Прогнозирующая динамическая модель конвертерного процесса. Известия вузов. Черная металлургия. 1979;22(4):128–131.
5. Chen J.D., Zhang C.J., Feng J.H. Static mechanics model in loading converter and energy saving. Journal of Hebei Institute of Technology. 2007;29(1):32–35.
6. Рожков И.М., Травин О.В., Туркенич Д.И. Математические модели конверторного процесса. Москва: Металлургия; 1978:184.
7. Pal J., Singh S., Ghose A.K., Mohan S. A mathematical model for end point control of basic oxygen steelmaking furnace. Journal of Metallurgy and Materials Science. 2002;44(1):39–49.
8. Cunha A.P., Pacianotto T.A., Frottini Fileti A.M. Steelmaking process: Neural models improve end-point predictions. Computer Aided Chemical Engineering. 2004;18(4): 631–636. https://doi.org/10.1016/S1570-7946(04)80171-8
9. Apeldoorn G.J., Gootjes P. Sublances for BOF steelmaking. In: Millennium Steel. 2006:97–101.
10. Бигеев А.М., Байтман В.В. Адаптация математической модели окончания продувки конвертерной плавки к условиям кислородно-конвертерного цеха Магнитогорского металлургического комбината. Металлург. 2006;(9):47–49.
11. Vortrefflich W., Vries J. Maximizing BOF production capacity and producing cost efficient by using sublance based process control. Iron & Steel Review. 2010;10:94–100.
12. Кошелев А.Е., Воронин Н.И., Петрунин М.В., Киселева Т.В., Турчанинов Е.Б. О косвенном контроле содержания углерода в конвертерной ванне. Известия вузов. Черная металлургия. 1981;24(12):105–110.
13. Хаазе Р. Термодинамика необратимых процессов. Москва: Мир; 1967:543.
14. Окороков Б.Н. Линейная энергодинамика открытых систем сталеплавильных процессов. Москва: Металлургиздат; 2021:520.
15. Dering D., Swartz C., Dogan N. Dynamic modeling and simulation of basic oxygen furnace (BOF) operation. Processes. 2020;8(4):483. https://doi.org/10.3390/pr8040483
16. Шулина Ж.М., Попель С.И., Шакиров К.М. Изменение межфазной поверхности жидкость-жидкость струей газа. Известия вузов. Черная металлургия. 1981;24(4):15–18.
17. Шакиров К.М., Толкунова И.Н., Рыбалкин Е.М., Шакиров М.К. Взаимодействие вертикальной струи газа со свободной поверхностью жидкости. В кн.: Тезисы докладов IV Всесоюзного семинара по газовым струям, 25 – 27 сентября 1990 г. Ленинград: ЛМИ; 1990:113.
18. Шакиров М.К. Совершенствование технологии внепечного рафинирования конвертерной стали на основе исследования и моделирования технологических стадий обработки. Автореф. дис. канд. техн. наук. Новокузнецк; 1998:23.
19. Протопопов Е.В., Уманский А.А., Морозов И.С., Шакиров М.К. Математическая модель режимов взаимодействия кислородных струй с расплавом при верхней продувке конвертерной ванны. Вестник Сибирского государственного индустриального университета. 2023;(3(45)):87–93. http://doi.org/10.57070/2307-4497-2023-3(45)-87-93
20. Шакиров К.М. Кинетика гетерогенных процессов. Развернутое кинетическое уравнение быстрых гетерогенных реакций в потоке. Новокузнецк: Издательский центр СибГИУ; 2012:76.
21. Есин О.А., Гельд П.В. Физическая химия пирометаллургических процессов. Ч. II. Взаимодействие жидкостей с газами и твердыми фазами. Москва: Металлургия; 1966:706.
22. Попель С.И., Сотников А.И., Бороненков В.Н. Теория металлургических процессов. Москва: Металлургия; 1986:463.
Об авторах
М. К. ШакировРоссия
Максим Кимович Шакиров, к.т.н., доцент кафедры автоматизации и информационных систем
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Е. В. Протопопов
Россия
Евгений Валентинович Протопопов, д.т.н., профессор кафедры металлургии черных металлов и химической технологии
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Е. Б. Турчанинов
Россия
Евгений Борисович Турчанинов, к.т.н., доцент кафедры автоматизации и информационных систем
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Е. А. Беленецкий
Россия
Евгений Анатольевич Беленецкий, магистрант кафедры металлургии черных металлов и химической технологии
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
С. С. Фатьянов
Россия
Сергей Сергеевич Фатьянов, магистрант кафедры металлургии черных металлов и химической технологии
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Рецензия
Для цитирования:
Шакиров М.К., Протопопов Е.В., Турчанинов Е.Б., Беленецкий Е.А., Фатьянов С.С. Комплексная энергодинамическая модель конвертерной плавки. Известия высших учебных заведений. Черная Металлургия. 2025;68(3):209-217. https://doi.org/10.17073/0368-0797-2025-3-209-217
For citation:
Shakirov M.K., Protopopov E.V., Turchaninov E.B., Belenetskii E.A., Fat’yanov S.S. Complex energy-dynamic model of BOF melting. Izvestiya. Ferrous Metallurgy. 2025;68(3):209-217. https://doi.org/10.17073/0368-0797-2025-3-209-217
JATS XML