Scroll to:
Complex energy-dynamic model of BOF melting
https://doi.org/10.17073/0368-0797-2025-3-209-217
Abstract
In practice, so-called static models are widely used to show the oxygen converter process, describing changes in output parameters based on information about input parameters for each individual production cycle (heat). Additionally, the models used in the final period make it possible to ensure a more accurate hit within the specified limits in terms of temperature and carbon content in the metal. In this case, information on the results of intermediate measurement of metal parameters by a probe tuyere, which is carried out during the consumption of 80 – 95 % of the total oxygen consumption for heat, is used as the initial information. To describe the behavior of an object during the process from the beginning to the end of the production cycle, it is necessary to build a model based on the patterns of phase interaction in an open system (oxygen converter – BOF). In this paper, an attempt is made to construct such a model using the concept of a stationary nonequilibrium state and the results of physical and mathematical modeling of the system when the contact area of two non-miscible liquids changes when exposed to a gas jet. When forming the model, we proceeded from the presence in the melt of two main reaction zones of oxidation of components, which, according to modern concepts, determine the mechanism of processes and hydrodynamics of the melt during blowing of the converter bath. For each selected zone, to a large extent, the characteristics of mass transfer during different periods of the operation, depending on the current parameters of the interacting phases, determine the rates of chemical reactions. The results of checking the adequacy of the model using practical data allow us to conclude that the model can be used to study the blowing process in a BOF.
Keywords
For citations:
Shakirov M.K., Protopopov E.V., Turchaninov E.B., Belenetskii E.A., Fat’yanov S.S. Complex energy-dynamic model of BOF melting. Izvestiya. Ferrous Metallurgy. 2025;68(3):209-217. https://doi.org/10.17073/0368-0797-2025-3-209-217
Introduction
Providing a detailed description of the processes taking place in an oxygen converter is a complex, multifactorial task. In practice, so-called static models and end-of-blow models are widely used to control the BOF process and achieve the target parameters of the semi-finished product. Static models [1 – 3] are based on the properties of the input materials and the desired characteristics of the semi-finished product at the end of the oxygen blowing. These models are primarily used to preliminarily calculate the required amounts of charge materials (scrap metal, hot metal), fluxes (lime, magnesia-based coolants, etc.), and oxygen per heat. To describe the cyclic nature of the steelmaking process, both theoretical [4 – 6] and statistical [7 – 9] models are typically applied. The models used in the final period (i.e., end-of-blow models) utilize the results of intermediate measurements of process parameters taken with a probe tuyere. These models help adjusting the initially fixed amounts of materials and oxygen to determine the optimal blowing endpoint [10 – 12]. However, such models do not provide real-time information on process parameters during blowing, which can may create certain difficulties when new materials or technological elements are introduced, as well as when optimizing blowing modes and overall process performance.
Problem statement and generalized model formulation
To accurately describe the processes occurring in the converter – including the influence of various parameters on both the progress and final outcomes of the operation – the following objective was set: to develop a generalized model grounded in the physicochemical principles that govern phase interaction patterns in the converter unit. The proposed model is based on the concept of a stationary nonequilibrium state (SNS) [13] and adopts the energy-dynamics approach introduced in [14]. Building on previous research [13 – 15], the model assesses the contact surface area between interacting phases and estimates the rates of heterogeneous reactions using data derived from physical and mathematical modeling [16 – 19].
To model the process, the system was initially decomposed into elements or interacting phases, each characterized by unique physicochemical properties. The active exchange between these phases necessitates an integrated assessment of interdependent parameters that describe their state and interaction throughout the operation.
The converter refining process is characterized by continuous changes in chemical reaction conditions:
– changes in quantities of interacting phases:
• liquid metallic (refined metal) and oxide (slag) phases;
• solid metallic (scrap) and oxide (fluxes, coolants, and the non-metallic component of the solid metal charge);
• gaseous phase, present in the slag–metal emulsion as CO bubbles and rising macrovolumes of off-gases;
– changes in chemical composition of the interacting phases:
• liquid metallic bath (refined metal);
• liquid oxide phase (slag);
• gaseous phase (rising gas bubbles);
– changes in temperature of the interacting phases;
– changes in blowing parameters, including the oxygen feed rate and the position of the lance relative to the surface of the metal bath in accordance with the selected blowing mode;
– changes in geometric parameters of the working space due to the wear of the refractory lining over the course of the converter campaign.
Quantities of interacting phases
Changes in the quantities of phases interacting in the converter result from the following processes:
– charge preparation: loading of scrap and pouring of hot metal, including possible presence of metal and slag from previous heats (including slag deposited on the unit lining as skull by various methods); addition of auxiliary materials (fluxes, coolants, solid and gaseous fuels) before and during blowing;
– phase transitions: melting and dissolution of solid components of metallic charge, fluxes and coolants in liquid metallic and oxide phases, as well as reverse processes; wear of the working layer of refractory lining;
– oxidation reactions of iron and impurities in the metal bath during interaction with oxygen jets;
– redox reactions and dissociation reactions at phase interfaces.
The change in quantity of the f-th phase during any blowing period can be generally described by the following expression:
| \[w_f^t = w_f^{t - 1} + \sum\limits_{g = 1}^G {\Delta {w_{gf}}} + \sum\limits_{h = 1}^H {\Delta {w_{hf}}} + \sum\limits_{i = 1}^I {\Delta {w_{if}}} + \sum\limits_{j = 1}^J {\Delta {w_{jf}}} ,\] | (1) |
where \(w_f^t\) and \(w_f^{t - 1}\) are the quantities of the f-th phase at the end of the current period and at the end of the previous blowing period, respectively; ∆wgf is the change in quantity of the f-th phase due to loading/addition of the g-th material into the converter that does not form a separate phase; ∆whf is the change in quantity of the f-th phase due to phase transition from the h-th phase to the f-th phase or the reverse process; ∆wif is the change in quantity of the f-th phase due to changes in quantities of reagents and products resulting from the i-th oxidation reaction with gaseous oxygen; ∆wjf is the change in quantity of the f-th phase due to changes in quantities of reagents and products resulting from the j-th redox reaction at the slag-metal interface.
The solid metallic phase constitutes a mixture of metal charge components, potentially forming conglomerates during initial operation stages and developing surface accretion (“freeze-on”) on fragments of the solid metal charge. The solid oxide phase comprises various auxiliary materials not yet transitioned to liquid or gaseous states (fluxes, coolants, non-metallic portions of the solid charge, slag from previous heats).
Thus, individual constituents of both metallic and oxide phases exhibit distinct chemical compositions and physical properties which govern their interaction mechanisms and transition rates into the liquid phase.
Chemical composition of interacting phases
Changes in the chemical composition of interacting phases result from the same processes that drive variations in phase quantities.
The general expression for the change in content of element (oxide) X in phase f during any blowing period is:
| \[[X]_f^t = \frac{{[X]_f^{t - 1}w_f^{t - 1} + \sum\limits_{p = 1}^P {\Delta {w_{Xp}}} }}{{w_f^t}},\] | (2) |
where \([X]_f^t\) and \([X]_f^{t - 1}\) is the content of element (oxide) X in phase f at the end of the current and previous blowing periods, respectively; p is the process stage identifier (material addition, phase transition, oxidation in the primary zone, oxidation/reduction at the slag-metal interface); ∆wXp is the change in quantity of element (oxide) X in phase f due to process p during the current blowing period.
Temperature of interacting phases
The temperature changes in interacting phases result from the following processes:
– heat exchange between phases, characterized by their current thermophysical properties (temperature, heat capacity, quantity);
– oxidation reactions (of iron and impurities), reduction reactions (of iron, manganese, and phosphorus oxides), and dissociation reactions (of hydroxides and carbonates), with heat release or absorption;
– phase transitions (characterized by transition enthalpies);
– energy exchange with the environment (heat losses through the refractory lining, radiation, and carried away by exhaust gases).
To quantify temperature changes during any blowing period, the following expression was used:
| \[\begin{array}{c}{T^t} = {T^{t - 1}} + \\ + \frac{{\sum\limits_{a = 1}^A {{H_a}w_a^t} - \sum\limits_{i = 1}^I {\Delta {H_i}\Delta w_{ir}^t} - \sum\limits_{h = 1}^H {\Delta {H_h}\Delta w_h^t} - \sum\limits_{l = 1}^L {{H_l}w_l^t} }}{{\sum\limits_{f = 1}^F {C_{pf}^tw_f^t} }},\end{array}\] | (3) |
where Ha and \(w_a^t\) are the specific enthalpy and the quantity of material a added to the converter in the current blowing period t; ∆Hi and ∆\(w_{ir}^t\) are the enthalpy of reaction i (per unit of reagent r) and the change in quantity of reagent r in period t; ∆Hh and ∆\(w_h^t\) are the phase transition enthalpy (per unit of phase h) and the quantity of phase undergoing transition in period t; Hl and \(w_l^t\) are the specific enthalpy and the quantity of gas l exiting the converter with exhaust gases in period t; \(C_{pf}^t\) and \({w_f^t}\) are the specific heat capacity (at constant pressure) and the quantity of condensed phase f at the end of period t.
Specific enthalpies of substances and reaction enthalpies are derived from standard reference data and temperature-dependent heat capacity functions.
Blowing mode parameters
Changes in oxygen blowing parameters are determined by process objectives at different stages:
– intensive slag formation during initial blowing;
– maintaining dynamic equilibrium between iron (and impurity) oxidation and carbon oxidation (during intense decarburization) processes;
– ensuring the metal’s chemical composition reaches specified limits during the final blowing stage.
Phase interaction conditions vary depending on blowing parameters (intensity, tuyere position above bath level), as well as temperature, quantities of metal and slag, and geometric characteristics of the working space.
Reaction rates and interfacial contact area
The rate of chemical reactions is governed by the following current parameters:
– phase composition of the system;
– temperature;
– current concentrations of initial components and reaction products in the interacting phases;
– concentrations of initial components and reaction products in the interacting phases under stationary nonequilibrium state.
The concentrations of slag and metal components were defined as their respective contents within the liquid oxide and liquid metallic phases. It was assumed that chemical reactions occur exclusively with the participation of liquid and gaseous phases. Thus, both the quantities and concentrations of the components in the liquid phases may vary in each calculation interval, partly due to phase transitions.
The total amount of slag was determined as sum of the solid and liquid oxide phases, whereas the total amount of metal was calculated as the sum of the solid and liquid metallic phases.
The general form of a chemical reaction rate equation is as follows
| V0 = kv Am Bn , | (4) |
where kv is the reaction rate constant, a function of temperature independent of the concentrations of reactants; A, B are the concentrations of reactants; and m, n represent the reaction orders with respect to reactants A and B, respectively.
The kinetic equation for a heterogeneous reaction describes the reaction rate as the number of elementary interaction events occurring per unit time per unit interfacial area.
Based on the considerations presented, to calculate the values of ∆wif and ∆wjf from equation (1) and ∆wXp from equation (2), it is necessary to estimate the contact area between interacting phases.
As demonstrated in [3; 14], oxidation reactions occur at the interfaces between interacting phases within distinct reaction zones of the converter bath:
– primary reaction zone: the interface between the oxygen jets and surface of the liquid metal;
– secondary reaction zone: the interface between the gaseous phase and the liquid metal and slag phases.
The oxidation rate of an impurity element was determined as the sum of the individual reaction rates in both zones.
Primary reaction zone. This zone represents the area of direct oxygen uptake from the blowing jets. In the primary zone, the oxidation reactions of silicon, manganese, and phosphorus – as well as carbon, when its concentration exceeds the transitional and critical levels – are assumed to occur under kinetic control. These oxidation reactions are considered first-order, with the oxygen concentration in the gas phase at the liquid metal interface taken as constant and equal to unity. Under these assumptions, the oxidation rate of an impurity element X is given by:
| V1X = kv S1[X], | (5) |
where kv is the reaction rate constant; S1 is the current contact area between the oxygen jets and the liquid metal; [X] is the current concentration of the oxidized element in the liquid metal.
At lower (subcritical) carbon concentrations – where the process is limited by mass transfer of carbon to the reaction zone (diffusion-controlled regime) – carbon oxidation rate can be expressed as
| V1C = km S1([C] – [C]*), | (6) |
where km is the mass transfer coefficient of carbon in the liquid metal; [C] is the current carbon concentration in the melt; [C]* is the limiting concentration of carbon, which depends on the characteristics of the blowing equipment and geometric parameters of the converter’s working space.
Secondary reaction zone. At lower concentrations, oxidation of silicon, manganese, phosphorus, and carbon primarily proceeds under diffusion-controlled conditions. To describe the rate of these processes, taking into account the contact area between the interacting condensed phases, the following form of the kinetic equation can be used [20]:
| V2X = km S2([X] – [X]*), | (7) |
where km is the mass transfer coefficient; S2 is the current contact area between the interacting condensed phase; [X] is the current concentration of the element in the liquid metal, and [X]* is its equilibrium concentration (or the limiting attainable concentration in the case of carbon).
The equilibrium concentration of an element in the liquid metal can be calculated using the well-known temperature dependence of the equilibrium constant for the corresponding reaction:
| \[\ln K = \frac{a}{T} + b,\] | (8) |
where K is the equilibrium constant of the chemical reaction; Т is the current temperature; a, b are empirical constants.
Since the equilibrium constant of a chemical reaction is defined as the ratio of the product of the concentrations of the reaction products to the product of the concentrations of the reactants at equilibrium, an increase in the content of oxidation products in the slag – assuming all other conditions remain unchanged – leads to an increase in the value of [X]* and shifts the reaction rate toward negative values; that is, it promotes the preferential development of the reverse reaction, in accordance with equation (7). Conversely, an increase in the concentration of reactants raises the current value of [X], which results in a higher reaction rate in the forward direction.
To describe the rate of carbon oxidation in the secondary zone at so-called transitional concentrations, a kinetic equation of the following form is used [21; 22]:
| V2C = kv S2[C]m (FeO)n, | (9) |
where (FeO) is iron oxide content in slag.
The values of kv and km are the rate constants and mass transfer coefficients in equations (5) – (7), (9) can be approximated by linear temperature dependences.
Determining the contact area between interacting phases
The contact area between the oxygen jets and the liquid metal during blowing was approximated as a value directly proportional to the dynamic pressure of the oxygen jet at the nozzle exit and inversely proportional to the square of the lance height above the metal surface, in accordance with previously obtained data on jet penetration depth into the liquid bath [14].
Data obtained through physical and mathematical modeling [16 – 18] have helped clarify how various parameters affect the contact area between the metal and slag phases.
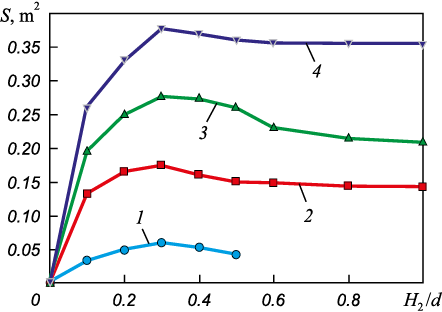
As a representative example, Figs. 1 and 2 [18] show the results of low-temperature modeling of metal–slag interaction under gas jet blowing conditions. The modeling demonstrated, for instance, that factors such as lance height (hl ), gas flow rate (q) and slag layer height (h2 ) influence the contact area S between the phases.
Fig. 1. Effect of slag layer height H2 , related to the reactor diameter d,
Fig. 2. Effect of slag layer height H2 , related to the reactor diameter d, |
In constructing the mathematical model, it is important to account for how the relative amount of slag in the converter bath changes over the course of blowing. This can be represented using the following parameter
| \[{H_2} = \frac{{{h_2}}}{{{d_{\rm{p}}}}},\] | (10) |
where dр is the diameter of the model.
The non-monotonic relationship between the interfacial area S and the total amount of slag can be attributed to the varying influence of the parameter H2 /d on the rate of droplet formation (vs ) – that is, the formation of metal droplets (or globules) suspended in the slag, which contribute to the additional interfacial area – and on their residence time during the heat (τs ):
| S = vs τs , | (11) |
The residence time of metal droplets (globules) in the slag is determined by the physical properties of the liquid phases, the characteristics of the gas jet, and the size of the main circulation loop for both the melt and the entrained droplets. In contrast, the rate of formation of additional interfacial area is governed by the blowing parameters and the thickness of the less dense, gas-saturated slag layer [18].
Afterburning of off-gases
The amount of carbon oxidized to CO and CO2 can be reasonably determined using the temperature-dependent equilibrium constant for the oxidation reaction of carbon monoxide with gaseous oxygen
| 2CO + O2 = 2CO2 . | (12) |
In this case, the reaction in the gas phase is assumed to proceed rapidly, with equilibrium established during the current blowing period, regardless of the time interval selected for the calculation.
Iron oxidation
The required amount of oxygen was determined based on the stoichiometric relationships for each oxidation reaction occurring during the current calculation interval in the primary and secondary reaction zones, as well as the afterburning of carbon monoxide CO.
To calculate the amount of oxygen consumed for iron oxidation during the current period, the total oxygen supplied to the bath – determined by the blowing mode parameters – was reduced by the amount used for the oxidation of impurity elements in the melt and for the afterburning of carbon monoxide CO:
| \[q_{{{\rm{O}}_2}}^{{\rm{Fe}}} = {q_{{{\rm{O}}_2}}} - \sum\limits_{i = 1}^N {q_{{{\rm{O}}_2}}^{{X_i}}} ,\] | (13) |
where \({q_{{{\rm{O}}_2}}}\) is the amount of oxygen introduced into the bath during the current period; \(q_{{{\rm{O}}_2}}^{{X_i}}\) is the amount of oxygen consumed for the oxidation of i-th element or carbon monoxide CO.
The amount of iron oxidized and the corresponding quantity of iron oxide formed were then calculated based on stoichiometric ratios.
For each reaction taking place, the heat effect corresponding to the quantities of reactants consumed and products formed was determined. The enthalpy of the off-gases, required for estimating heat losses (see Equation 3), was calculated as a function of gas heat capacity and temperature, the latter assumed equal to the current temperature of the condensed phases.
The reaction rates, calculated with consideration of the interfacial area between interacting phases, were applied in accordance with equations (1) – (3).
Melting/dissolution rate of materials in the melt
The mass rate of melting or dissolution of each additive material and steel scrap during the blowing process can be estimated using empirical expressions. These are typically expressed as linear functions of the current solid-phase amount and the average temperature of the condensed phases at the start of the current time interval. For instance, in the case of light scrap, the melting rate coefficients were adjusted so that, according to model calculations, the transition to the liquid phase would be completed within 20 – 30 % of the total blowing time. For heavy scrap, this transition occurred within 50 – 80 % of the blowing duration.
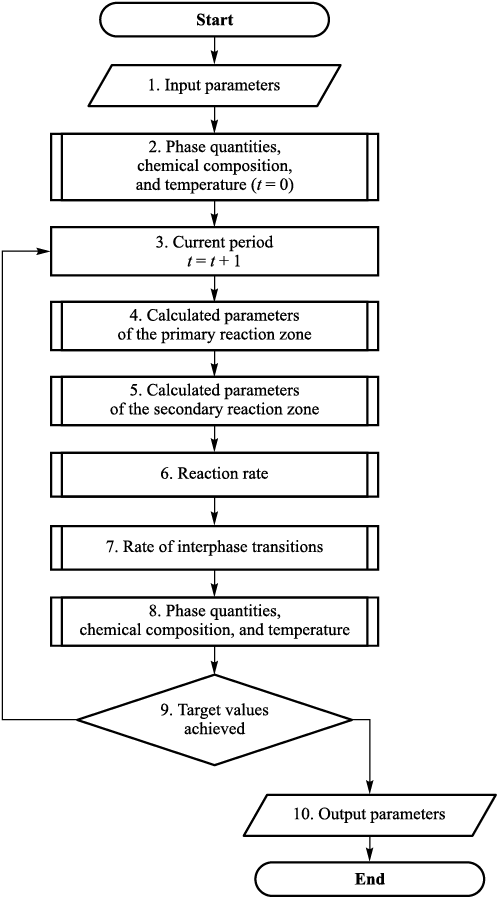
Accordingly, the model is designed to calculate the current values of the quantity, chemical composition, and temperature of the interacting phases at the end of each defined blowing interval. These values are then used as input data for the next interval. In practical applications, each time step in the calculation typically corresponds to the consumption of 200 m3 of oxygen. A generalized algorithm of the model is shown in Fig. 3.
Fig. 3. Enlarged algorithm of the model functioning |
Accordingly, the minimum required set of input data for calculations must include the following information:
– chemical composition and quantities of charge materials (hot metal and scrap) and additives (fluxes and coolants);
– temperature of the hot metal;
– predefined or actual parameters of the blowing mode (lance position, oxygen flow rate, etc.) and slag mode (material addition schedule during blowing);
– target or measured end-of-blow values: final temperature of the metal and the content of carbon, manganese, sulfur, and phosphorus.
Results and discussion
As a result of implementing this algorithm to solve the integrated problem, the model provided calculated values for the final temperature and chemical composition of the metal after blowing, the total oxygen consumption for the heat, and the trajectories of these parameters – along with those of the slag phase – throughout the operation.
The model’s adequacy was assessed using data from 200 heats carried out in a 350-ton converter under real production conditions, where additional process monitoring was performed using a probe tuyere. The assessment was based on actual process data, including material quantities, auxiliary material addition schedules, blowing parameters, total oxygen consumption, and the final chemical composition of the metal. Model calculations were halted once the carbon content in the metal reached the value actually observed in the corresponding heat. By tuning the model coefficients, the resulting outputs included the ranges (numerators) and average values (denominators) for key end-of-blow parameters (Table 1).
Table 1. Parameters of the end of blowing
|
Calculation errors ∆ for end-of-blow indicators were defined as the difference between measured and predicted values. Table 2 presents both the mean errors (numerators) and the mean absolute errors (denominators) of the calculations.
Table 2. Parameter prediction errors
|
Conclusions
The resulting error values for end-of-blow parameters confirm the adequacy of the model developed using the proposed approach. This, in turn, supports the model’s application for analyzing the effects of variations in material composition, quantity, and properties, as well as in process conditions and converter geometry, on the dynamics of phase interaction and end-of-blow outcomes – ultimately helping to reduce the need for corrective operations.
References
1. Turkenich D.I. Control of Steel Melting in a Converter. Moscow: Metallurgiya; 1971:360. (In Russ.).
2. Boichenko B.M., Nizyaev K.G., Stoyanov A.N., Molchanov L.S., Sinegin E.V. Parametrization of steel production in an oxygen converter. Sistemnye tekhnologii. 2017;(3(110)):10–15. (In Russ.).
3. Bigeev A.M. Mathematical Description and Calculations of Steelmaking Processes. Moscow: Metallurgiya; 1982:160. (In Russ.).
4. Mochalov S.P., Aizatulov R.S., Shakirov K.M. Predicting dynamic model of converter process. Izvestiya. Ferrous Metallurgy. 1979;22(4):128–131. (In Russ.).
5. Chen J.D., Zhang C.J., Feng J.H. Static mechanics model in loading converter and energy saving. Journal of Hebei Institute of Technology. 2007;29(1):32–35.
6. Rozhkov I.M., Travin O.V., Turkenich D.I. Mathematical Models of the Converter Process. Moscow: Metallurgiya; 1978:184. (In Russ.).
7. Pal J., Singh S., Ghose A.K., Mohan S. A mathematical model for end point control of basic oxygen steelmaking furnace. Journal of Metallurgy and Materials Science. 2002;44(1):39–49.
8. Cunha A.P., Pacianotto T.A., Frottini Fileti A.M. Steelmaking process: Neural models improve end-point predictions. Computer Aided Chemical Engineering. 2004;18(4): 631–636. https://doi.org/10.1016/S1570-7946(04)80171-8
9. Apeldoorn G.J., Gootjes P. Sublances for BOF steelmaking. In: Millennium Steel. 2006:97–101.
10. Bigeev A.M., Baitman V.V. Adaptation of mathematical model of BOF blowing end to conditions of BOF shop of Magnitogorsky Iron and Steel Works. Metallurg. 2006;(9):47–49. (In Russ.).
11. Vortrefflich W., Vries J. Maximizing BOF production capacity and producing cost efficient by using sublance based process control. Iron & Steel Review. 2010;10:94–100.
12. Koshelev A.E., Voronin N.I., Petrunin M.V., Kiseleva T.V., Turchaninov E.B. On indirect control of carbon content in converter bath. Izvestiya. Ferrous Metallurgy. 1981;24(12):105–110. (In Russ.).
13. Haase R. Thermodynamik der irreversiblen Prozesse. Steinkopff Heidelberg; 1963:554. (In Germ.). https://doi.org/10.1007/978-3-642-88485-6
14. Okorokov B.N. Linear Energy Dynamics of Open Systems of Steelmaking Processes. Moscow: Metallurgizdat; 2021:520. (In Russ.).
15. Dering D., Swartz C., Dogan N. Dynamic modeling and simulation of basic oxygen furnace (BOF) operation. Processes. 2020;8(4):483. https://doi.org/10.3390/pr8040483
16. Shulina Zh.M., Popel’ S.I., Shakirov K.M. Changing the liquid-liquid interface by a gas jet. Izvestiya. Ferrous Metallurgy. 1981;24(4):15–18. (In Russ.).
17. Shakirov K.M., Tolkunova I.N., Rybalkin E.M., Shakirov M.K. Interaction of a vertical gas jet with a free liquid surface. In: Abstracts of the IV All–Union Seminar on Gas Jets, September 25-27 1990. Leningrad: LMI; 1990:113. (In Russ.).
18. Shakirov M.K. Improving the technology of extra-furnace refining of converter steel based on research and modeling of technological processing stages: Extended Abstract of Cand. Sci. Diss. Novokuznetsk; 1998:23.
19. Protopopov E.V., Umanskii A.A., Morozov I.S., Shakirov M.K. Mathematical model of modes of interaction of oxygen jets with melt during upper purging of a converter bath. Bulletin of the Siberian State Industrial University. 2023;(3(45)):87–93. (In Russ.). http://doi.org/10.57070/2307-4497-2023-3(45)-87-93
20. Shakirov K.M. Kinetics of Heterogeneous Processes. An Expanded Kinetic Equation of Fast Heterogeneous Reactions in a Flow. Novokuznetsk: SibSIU Publishing Center; 2012:76. (In Russ.).
21. Esin O.A., Gel’d P.V. Physical Chemistry of Pyrometallurgical Processes. Part II. Interaction of Liquids with Gases and Solid Phases. Moscow: Metallurgiya; 1966:706. (In Russ.).
22. Popel’ S.I., Sotnikov A.I., Boronenkov V.N. Theory of Metallurgical Processes. Moscow: Metallurgiya; 1986:463. (In Russ.).
About the Authors
M. K. ShakirovRussian Federation
Maksim K. Shakirov, Cand. Sci. (Eng.), Assist. Prof. of Chair of Automation and Information Systems
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kusbass, 654007, Russian Federation
E. V. Protopopov
Russian Federation
Evgenii V. Protopopov, Dr. Sci. (Eng.), Prof. of the Chair of Ferrous Metallurgy and Chemical Technology
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kusbass, 654007, Russian Federation
E. B. Turchaninov
Russian Federation
Evgenii B. Turchaninov, Cand. Sci. (Eng.), Assist. Prof. of Chair of Automation and Information Systems
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kusbass, 654007, Russian Federation
E. A. Belenetskii
Russian Federation
Evgenii A. Belenetskii, MA Student of the Chair of Ferrous Metallurgy and Chemical Technology
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kusbass, 654007, Russian Federation
S. S. Fat’yanov
Russian Federation
Sergei S. Fat’yanov, MA Student of the Chair of Ferrous Metallurgy and Chemical Technology
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kusbass, 654007, Russian Federation
Review
For citations:
Shakirov M.K., Protopopov E.V., Turchaninov E.B., Belenetskii E.A., Fat’yanov S.S. Complex energy-dynamic model of BOF melting. Izvestiya. Ferrous Metallurgy. 2025;68(3):209-217. https://doi.org/10.17073/0368-0797-2025-3-209-217