Перейти к:
Методика расчета плоскостности стальных холоднокатаных полос
https://doi.org/10.17073/0368-0797-2025-4-417-423
Аннотация
Известной причиной возникновения дефектов плоской формы на готовых стальных холоднокатаных полосах является неравенство коэффициентов вытяжки по ширине полосы. На разницу значений этих коэффициентов оказывают влияние параметры профилировок бочек валков, энергосиловые параметры прокатки, параметры работы системы автоматического регулирования профиля и формы полосы. Воздействие всех технологических факторов на форму полосы будет иметь сложный характер. В работе рассмотрен подход, учитывающий основные параметры работы прокатного оборудования и позволяющий оценить вид и амплитуду дефектов плоскостности готовых стальных полос. При реализации такого подхода выполнены шесть этапов расчета: энергосиловой расчет процесса холодной прокатки; расчет упругих деформаций поверхности бочки рабочего валка; оценка износа поверхности бочки рабочего валка; расчет теплового профиля валка; оценка выпуклости поперечного профиля стальной полосы; оценка показателей планшетности готовой полосы. Для вычисления параметров, влияющих на планшетность проката, использованы известные методики расчета, адаптированные под конкретные технологические условия. Результаты оценки показателей формы катаной полосы, полученные с помощью модели, сопоставлены с результатами моделирования в программе Deform 3D. Результаты моделирования продемонстрировали достоверность предложенного подхода оценки качества проката.
Ключевые слова
Для цитирования:
Шалаевский Д.Л. Методика расчета плоскостности стальных холоднокатаных полос. Известия высших учебных заведений. Черная Металлургия. 2025;68(4):417-423. https://doi.org/10.17073/0368-0797-2025-4-417-423
For citation:
Shalaevskii D.L. Methodology for calculating the flatness of cold-rolled steel strips. Izvestiya. Ferrous Metallurgy. 2025;68(4):417-423. https://doi.org/10.17073/0368-0797-2025-4-417-423
Введение
Основные причины потери стальной катаной полосой плоской формы – неравномерная ее деформация по ширине, а также малая жесткость ее сечения. Последний фактор неплоскостности относится к характеристикам плоского проката.
Подавляющее количество авторов известных трудов в качестве основного критерия потери плоской формы использует разность коэффициентов вытяжки по ширине полосы. При этом отдельные влияющие параметры считаются более значимыми, другие – менее значимыми [1 – 18].
В работах [2 – 4] приведены критерии прокатки плоской полосы на основе только лишь значений коэффициентов вытяжки по ширине полосы. Результаты исследований, представленные в публикациях [5 – 8], демонстрируют возможность оценки дефекта плоскостности полосы по характеристикам ее сечения.
Модели, основанные на учете комплекса технологических параметров при оценке планшетности полосы, приведены в трудах [9 – 11].
В работах [12 – 14] представлены подходы, при реализации которых идентификация дефектов плоской формы осуществляется по характеристикам поперечного профиля проката.
Модели, ставящие в основу причин потери плоскостности полосы технологию ее охлаждения после прокатки, приведены в трудах [15 – 18].
Методика оценки планшетности, упомянутая в работе [9], позволяет выполнять расчет амплитуды неплоскостности по параметрам процесса прокатки. Эта методика учитывает практически все влияющие факторы, например, такие, как профилировка бочки рабочих валков, ее возможный износ, перекос осей рабочих валков и ряд других значимых факторов.
В рамках исследования ставилась задача разработки методики оценки амплитуды волнистости и коробоватости холоднокатаной полосы на основе разности коэффициентов вытяжки по ширине, ее дальнейшая апробация путем сравнения результатов расчета и моделирования в программе Deform 3D.
Постановка задачи и методы исследования
Расчет амплитуды «волны» или «короба», исходя из разности коэффициентов вытяжки полосы по ее ширине, требует данных об упругих деформациях рабочих и опорных валков, износе поверхности их бочек, а также сведения о неравномерности их тепловых расширений на ширине прокатываемой полосы.
В работе [19] представлена регрессионная зависимость упругих деформаций клети «кварто» по длине бочки рабочего валка, полученная путем моделирования численным методом упругих деформаций валковой системы «кварто». Предложенная зависимость ранее была применена в модели формирования плоскостности горячекатаных полос на непрерывном широкополосном стане и может быть использована в рамках вновь предлагаемой комплексной методики.
Также известны работы, которые позволяют оценить износ поверхности бочек и их неравномерное тепловое расширение по длине валка [20 – 22].
Оценка вида и амплитуды дефекта плоскостности стальной катаной полосы может быть выполнена по методике, представленной в работе [23].
Достоверность полученных таким образом результатов могла бы быть проверена путем оценки показателей качества формы плоского проката в программе Deform.
Результаты работы и их обсуждение
Порядок расчета вида и амплитуды дефекта плоской формы холоднокатаной полосы включал в себя следующие этапы:
– первый этап – энергосиловой расчет процесса холодной прокатки;
– второй этап – расчет упругих деформаций поверхности бочки рабочего валка;
– третий этап – оценка износа поверхности бочки рабочего валка;
– четвертый этап – расчет теплового профиля валка;
– пятый этап – оценка выпуклости поперечного профиля стальной полосы;
– шестой этап – оценка показателей планшетности готовой полосы.
Первый этап реализован с использованием модели энергосиловых параметров, учитывающей участки упругого деформирования по длине очага деформации [24 – 25].
Второй этап выполнен путем моделирования упругих деформаций валковой системы клети «кварто» с помощью программы, использующей численные методы при исследовании механики процессов.
Для определения деформации поверхности бочки рабочего валка с учетом упругого сплющивания в зонах ее контакта с бочкой опорного валка и полосы при прокатке были созданы трехмерные компьютерные модели комплектов рабочих и опорных валков клети пятиклетевого непрерывного стана холодной прокатки 1700.
Комплект валков был импортирован в модуль Mechanical Structure программы Ansys R1 (рис. 1).
Рис. 1. Модель валковой системы клети «кварто» |
В препроцессоре данного модуля была сгенерирована сетка (рис. 1), в качестве материала валков в интеграторе AnsysWorkbench задана высокоуглеродистая сталь с пределом текучести 900 МПа. Для имитации опор в качестве граничных условий для шеек опорного валка были наложены ограничения по перемещению в направлении осей X, Y и Z (вертикальное направление), а для имитации опор рабочего валка введены ограничения на перемещение вдоль осей X, Y. В вертикальном направлении рабочий валок опирается на бочку опорного.
Заранее при создании твердотельной модели на поверхности бочки рабочего валка определили область, по которой будет распределено контактное давление в очаге деформации и в этой области приложили давление, равное нормальному напряжению в очаге деформации. Для этого предварительно был запущен решатель StaticStructure.
Для имитации усилия противоизгиба на торцы шеек рабочих валков приложили сосредоточенные силы, направленные вертикально по направлению оси Y.
Профилировку бочек рабочего и опорного валков, контактное давление в очаге деформации, ширину прокатываемой полосы и усилие противоизгиба рабочих валков изменяли при моделировании в установленном диапазоне.
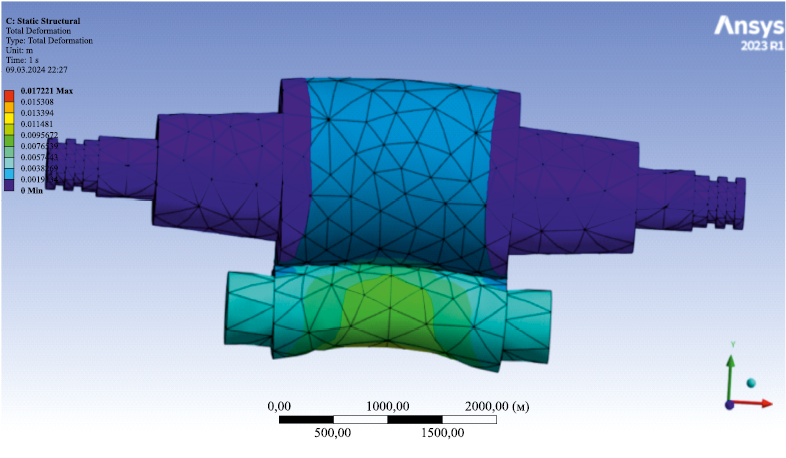
Цветовая диаграмма, демонстрирующая результат расчета упругих деформаций, представлена на рис. 2.
Рис. 2. Пример результата расчета упругих деформаций в вертикальной осевой плоскости |
Результаты расчета разности упругих деформаций поверхности бочки рабочего валка у кромки полосы и в ее середине (упругий прогиб по ширине полосы) были обобщены в виде регрессионного уравнения
| Δдс – Δдкр = 0,00001632·10–5b + 0,007703P – – 0,00000305Pизг – 0,0200ΔDш.с. – 0,0169ΔDш.с.оп , | (1) |
где P – сила прокатки в i-ой клети, МН; Pизг – сила противоизгиба рабочих валков, кН; b – ширина полосы, мм; ΔDш.с. – шлифовочная выпуклость бочки рабочего валка в ее середине, мм; ΔDш.с.оп – шлифовочная выпуклость бочки опорного валка в ее середине, мм.
Коэффициент множественной детерминации R2 составил 0,86, что показывает высокую достоверность полученной зависимости.
Значимость коэффициентов в уравнении (1) оценили с помощью уровня статистической значимости (p-value), используя набор данных из результатов сорока вариантов моделирования, ранее представленных в работе [19]. Результаты проверки приведены в табл. 1.
Таблица 1. Результаты проверки значимости коэффициентов уравнения
| ||||||||||||||
Третий этап – оценка износа поверхности бочки рабочего валка выполнена на основе экспериментальных данных, содержащих параметры работы валка, данные о твердости его поверхности и профилировки [20].
Данные табл. 2 демонстрируют, что на износ влияют усилие прокатки, твердость поверхности бочки валка, диаметр его бочки и количество прокатанной на нем стальной полосы. Исходная вогнутость оказывает несущественное воздействие.
Таблица 2. Результаты оценки коэффициентов корреляции Пирсона
|
Определена зависимость износа бочки валка в ее середине и у кромок полосы от установленных влияющих факторов:
| Δc = kP P + kL Lм , | (2) |
где P – средний уровень усилия прокатки в рабочей клети с момента завалки рабочего валка в клеть, МН; Lм – длина полосы, прокатанной на рабочих валках в клети м; kP – коэффициент влияния усилия прокатки на износ поверхности бочки рабочего валка; kL – коэффициент влияния длины полосы, прокатанной на рабочих валках в клети.
Значение этих коэффициентов, например, для середины бочки валка, определены уравнением (в середине ширины полосы)
| kP = –0,00025HSD + 0,0000285D, | (3) |
где HSD – твердость поверхности бочки валка по шкале Шора, D – диаметр бочки рабочего валка, мм (значение коэффициента множественной детерминации уравнения составил R2 = 0,89);
| kL = –0,0000011HSD + 0,00000011D. | (4) |
Четвертый этап – расчет теплового профиля бочки валка.
Расчет теплового режима непрерывного стана холодной прокатки производится путем составления и совместного решения уравнений теплового баланса рабочих и опорных валков, а также полосы. Использование такой модели для процессов непрерывной холодной и горячей прокатки стальной полосы представлено в уже упомянутых работах [21; 22].
Тепловая выпуклость бочки валка по ширине полосы рассчитается с учетом найденной из системы уравнений температуры бочки валка в ее середине.
Пятый этап – оценка профиля полосы, может быть выполнена с учетом найденных на предыдущих этапах расчета компонент, определяющих форму сечения готового плоского проката на выходе из валков:
– исходная шлифовочная профилировка с учетом ее текущего износа, Δшy ;
– упругая деформация поверхности бочки валка, Δдy ;
– тепловой профиль (тепловая выпуклость) поверхности бочки валка, Δтy ;
– номинальная толщина полосы, hi .
Толщина полосы в произвольной точке по ее ширине с координатой y составит:
| Δiy = hi – Δшy + Δдy – Δтy . |
Шестой этап – оценка показателей планшетности готовой полосы, может быть реализована с применением зависимостей, представленных в работе [23].
Зная толщины подката и проката по их ширине и, следовательно, коэффициенты вытяжки у кромок полосы и в ее середине, возможно оценить наиболее важный параметр дефекта планшетности по ГОСТ 19903 – 2015 – амплитуду дефекта плоскостности:
– «волна», образовавшаяся в i-ой клети непрерывной группы клетей:
| \[{a_{{\rm{в}}i}} = \frac{{hE\left[ {1 - \cos \left( {\frac{{2{{\rm{\sigma }}_{\rm{к}}}\left( {{{\rm{\lambda }}_{{\rm{кр}}}} - {{\rm{\lambda }}_{\rm{c}}}} \right)}}{{hE}}} \right)} \right]}}{{{{\rm{\sigma }}_{\rm{к}}}}},\] | (5) |
где h – толщина полосы, E – модуль упругости полосы, σк – критическое напряжение потери устойчивости, λкр , λс – коэффициенты вытяжки у кромки полосы и в середине ее ширины, определяемые, исходя из формы сечения подката и полосы на выходе из валков;
– «короб», образовавшийся в i-ой клети непрерывной группы клетей:
| \[{a_{{\rm{к}}i}} = \frac{{hE\left[ {1 - \cos \left( {\frac{{2{{\rm{\sigma }}_{\rm{к}}}\left( {{{\rm{\lambda }}_{\rm{c}}} - {{\rm{\lambda }}_{{\rm{кр}}}}} \right)}}{{hE}}} \right)} \right]}}{{{{\rm{\sigma }}_{\rm{к}}}}}.\] | (6) |
При этом подтверждено [23], что дефект планшетности полосы будет «накапливаться» на полосе от клети к клети. Тогда, если тот же вид дефекта планшетности проявится в последующих клетях, то амплитуды его будут суммироваться.
Оценку достоверности расчета вида и амплитуды волны по формулам (4) и (5) выполнили путем моделирования процесса прокатки в программе Deform 3D. Для этого создали бочки валков с продольным профилем, учитывающим упругую деформацию и тепловую выпуклость бочки на ширине полосы. Также возможно учесть неравномерный износ поверхности бочки. Создали подкат с заданным профилем поперечного сечения и промоделировали технологический процесс. В постпроцессоре оценили путем отслеживания точек по ширине полос разность перемещений в вертикальном направлении середины и кромки полосы.
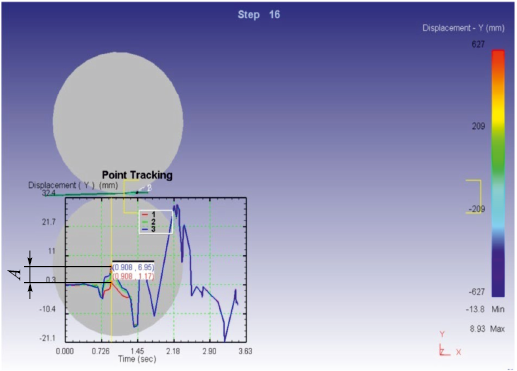
На рис. 3 линия 3 показывает перемещение в вертикальном направлении точки полосы у ее кромки, линия 1 – в середине ширины полосы. Разницу в перемещении в вертикальном направлении кромки полосы и середины ее ширины принимали за амплитуду дефекта.
Рис. 3. Пример оценки дефекта плоскостности полосы «волна» |
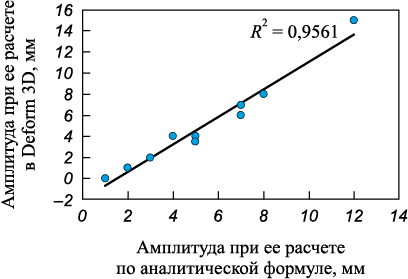
Пример оценки амплитуды в программе Deform 3D представлен на рис. 4.
Рис. 4. Сравнение результатов расчета амплитуды неплоскостности |
Результаты оценки достоверности аналитической методики с использованием данных, полученных в программе Deform 3D, демонстрируют достаточную достоверность модели для применения ее при прогнозировании плоскостности холоднокатаной полосы.
Выводы
Известной причиной возникновения дефектов плоской формы на готовых стальных холоднокатаных полосах является неравенство коэффициентов вытяжки по ширине полосы. На разницу значений этих коэффициентов оказывают влияние параметры профилировок бочек валков, энергосиловые параметры прокатки, параметры работы системы автоматического регулирования профиля и формы полосы. Воздействие всех технологических факторов на форму полосы будет иметь сложный характер. В работе рассмотрен подход, учитывающий основные параметры работы прокатного оборудования, позволяющий оценить вид и амплитуду дефектов плоскостности готовых стальных полос.
Список литературы
1. Shalaevskii D.L. Models for the formation of flatness defects of steel strip during its rolling and heat treatment. Russian Metallurgy (Metally). 2024;2024(7):1760–1764. https://doi.org/10.1134/S0036029524703063
2. Будаква А.А., Коновалов Ю.В., Ткалич К.Н. Профилирование валков листовых станов. Киев: Техника; 1986:190.
3. Максимов Е.А., Шаталов Р.Л., Босхамджиев Н.Ш. Производство планшетных полос при прокатке. Москва: Теплотехник; 2008:355.
4. Шаталов Р.Л., Максимов Е.А., Верхов Е.Ю. Рациональные режимы управления плоскостностью полос при тонколистовой реверсивной прокатке / Научно‐технический прогресс в черной металлургии: Материалы II Международной научно‐технической конференции (7 – 9 октября 2015 г.). Череповец: Череповецкий государственный университет; 2015:148–151.
5. Шаталов Р.Л., Максимов Е.А. Уточнение метода расчета критических напряжений и показателей плоскостности полосы при тонколистовой прокатке. Сталь. 2016; (4):26–30.
6. Иевлев Н.Г. Математические модели плоскостности толстолистового проката применительно к АСУ ТП. Математичні машини і системи. 2018;(1):67–77.
7. Шаталов Р.Л., Максимов Е.А. Анализ эффективности технологии асимметричной прокатки для повышения точности прокатываемых полос. Металлург. 2016;(7):80–84.
8. Бартхольдт Х., Копин Ф., Джелали М. Универсальная модель плоскостности для оптимизации процесса холодной прокатки. Черные металлы. 2015;(3):53–58.
9. Шалаевский Д.Л., Митрофанов А.В., Корепина К.П. Повышение плоскостности готовых стальных полос на энергосберегающих режимах непрерывной горячей прокатки. Сталь. 2022;(2):15–17.
10. Гарбер Э.А., Шалаевский Д.Л., Мишнев П.А., Михеева И.А., Палигин Р.Б. Улучшение плоскостности горячекатаных стальных широких полос путем оптимизации настройки параметров технологического режима / Всероссийская научно-практическая конференции «Проблемы черной металлургии – 2015. Международный научный семинар». 2016:76–82.
11. Григорян Г.Г., Железнов Ю.Д., Черный В.А. и др. Настройка, стабилизация и контроль процесса тонколистовой прокатки. Москва: Металлургия; 1983:120.
12. Пименов В.А., Бельский С.М., Кузнецова Е.В., Шкарин А.Н. Математическая модель идентификации формы профиля поперечного сечения горячекатаных полос и распределения вытяжек по ширине холоднокатаных полос. Сообщение 1. Производство проката. 2018;(1):11–15.
13. Пименов В.А., Бельский С.М., Кузнецова Е.В., Шкарин А.Н. Математическая модель идентификации формы профиля поперечного сечения горячекатаных полос и распределения вытяжек по ширине холоднокатаных полос. Сообщение 2. Производство проката. 2018;(6):9–14.
14. Шкарин А.Н. Формирование плоскостности холоднокатаных полос с учетом особенностей профиля поперечного сечения горячекатаного подката: Автореферат диссертации … кандидата технических наук. 2021.
15. Wang X., Yang Q., He A. Calculation of thermal stress affecting strip flatness change during run-out table cooling in hot steel strip rolling. Journal of Materials Processing Technology. 2008;207(1-3):130–146. https://doi.org/10.1016/j.jmatprotec.2007.12.076
16. Hrabovsky J., Pohanka M., Lee P.J., Kang J.H. Experimental and numerical study of hot-steel-plate flatness. Materials and Technology. 2016;50(1):17–21. https://doi.org/10.17222/mit.2014.153
17. Wu H., Sun J., Lu X., Peng W. Predicting stress and flatness in hot-rolled strips during run-out table cooling. Journal of Manufacturing Processes. 2022;84:815–831. https://doi.org/10.1016/j.jmapro.2022.10.053
18. Божков А.И., Ковалев Д.А., Черников О.В., Юсупов В.С., Ивлиев С.Н., Дегтев С.С. Влияние режимов термообработки на плоскостность полос электротехнических изотропных сталей. Сообщение 2. Сталь. 2019;(2):26–28.
19. Шалаевский Д.Л. Прогнозирование плоскостности стальной полосы на основе разности коэффициентов вытяжек по ее ширине при прокатке. Черная металлургия. Бюллетень научно-технической и экономической информации. 2024;80(10):20–27.
20. Шалаевский Д.Л., Сидоров А.В. Исследование износа поверхности бочек рабочих валков непрерывной группы клетей широкополосного стана горячей прокатки. Заготовительные производства в машиностроении. 2024;22(7):315–318. https://doi.org/10.36652/1684-1107-2024-22-7-315-318
21. Гарбер Э.А. Станы холодной прокатки: (теория, оборудование, технология). Москва: ОАО “Черметинформация”; 2004:412.
22. Шалаевский Д.Л. Исследование теплового режима рабочих валков стана горячей прокатки с целью повышения точности расчета температур поверхностей их бочек. Известия вузов. Черная металлургия. 2023; 66(3):283–289. https://doi.org/10.17073/0368-0797-2023-3-283-289
23. Шалаевский Д.Л. Исследование влияния технологических факторов при непрерывной горячей прокатке на плоскостность тонких стальных листов с целью повышения их качества. Металлы. 2024;(5):62–68. https://doi.org/10.31857/S0869573324056268
24. Shalaevskiy D.L., Kozhevnikov A.V. Algorithm and design methodology for energy-efficient sheet products production technology. IOP Conference Series: Materials Science and Engineering. 2020;718:012015. https://doi.org/10.1088/1757-899X/718/1/012015
25. Garber E.A., Shalaevskii D.L., Kozhevnikova I.A., Traino A.I.
26. Procedure and algorithms for the energy-force calculation of cold rolling allowing for the number of neutral sections in the deformation zone. Russian Metallurgy (Metally). 2008;2008(4):315–325. https://doi.org/10.1134/S0036029508040083
Об авторе
Д. Л. ШалаевскийРоссия
Дмитрий Леонидович Шалаевский, к.т.н., доцент кафедры металлургии, машиностроения и технологического оборудования
Россия, 162600, Вологодская обл., Череповец, пр. Луначарского, 5
Рецензия
Для цитирования:
Шалаевский Д.Л. Методика расчета плоскостности стальных холоднокатаных полос. Известия высших учебных заведений. Черная Металлургия. 2025;68(4):417-423. https://doi.org/10.17073/0368-0797-2025-4-417-423
For citation:
Shalaevskii D.L. Methodology for calculating the flatness of cold-rolled steel strips. Izvestiya. Ferrous Metallurgy. 2025;68(4):417-423. https://doi.org/10.17073/0368-0797-2025-4-417-423