Перейти к:
Использование цифровых имитационных моделей для оптимизации работы сложных производственных объектов
https://doi.org/10.17073/0368-0797-2025-2-188-194
Аннотация
На примере формализованного описания работы конвертерного производства АО «ЕВРАЗ Объединенный Западно-Сибирский металлургический комбинат» в составе двух конвертерных цехов с двумя и тремя агрегатами показано, что вопросы планирования объемов производства и ремонтов металлургических агрегатов, построения сквозных графиков работы агрегатов являются сложными и многофакторными задачами, которые характеризуются дискретностью и нелинейностью описывающих их функционалов. Формализация задач оптимизации производственных процессов с заданными ограничениями и критериями показала, что особенности исследуемого процесса функционирования конвертерного производства делают практически невозможными построение и использование аналитических решений. Выбранный авторами подход к решению (с учетом указанных обстоятельств) базируется на использовании цифровой дискретно-событийной имитационной модели. Такая имитационная модель представляет собой цифровую копию исследуемого процесса функционирования конвертерного производства, отражает его структуру, производительность, техническое состояние и такие параметры, как длительность кампании конвертеров, длительность ремонтных периодов и др. Модель использует различные механизмы управления для решения задач распределения входного потока чугуна между конвертерными цехами, формирования календарных графиков работы отдельных конвертеров и их ремонтов; накапливает информацию в ходе производственного процесса для целей оптимизации и прогнозирования результатов процесса функционирования; позволяет собирать данные о процессе функционирования конвертерного производства и использовать инструменты предиктивной аналитики для планирования ремонтов; предоставляет данные, которые невозможно получить непосредственно на физическом объекте и которые могут быть использованы для оптимизации параметров системы; формирует наборы данных для визуализации отдельных результатов процесса функционирования.
Ключевые слова
Для цитирования:
Зимин А.В., Корнет М.Е., Буркова И.В., Зимин В.В. Использование цифровых имитационных моделей для оптимизации работы сложных производственных объектов. Известия высших учебных заведений. Черная Металлургия. 2025;68(2):188-194. https://doi.org/10.17073/0368-0797-2025-2-188-194
For citation:
Zimin A.V., Kornet M.Е., Burkova I.V., Zimin V.V. Using digital simulation models to optimize the operation of complex production facilities. Izvestiya. Ferrous Metallurgy. 2025;68(2):188-194. https://doi.org/10.17073/0368-0797-2025-2-188-194
Введение
Задачи планирования ремонтов и календарных графиков работы конвертеров сталеплавильного производства металлургического комбината имеют существенные особенности, что обусловлено дискретностью, нелинейностью и сильной взаимозависимостью задач. Решение таких задач целесообразно получать как комплексный результат решения некоторой общей задачи, не подвергнутой декомпозиции, так как операция декомпозиции при сильных связях не позволяет получать устойчивые и эффективные решения частных задач в силу ограничений, которые накладываются процедурой декомпозиции [1; 2]. Однако получение комплексного решения аналитическими средствами для рассматриваемого объекта планирования представляет большую сложность (если вообще является возможным). В связи с этим авторы исследования приняли решение о построении дискретно-событийной цифровой имитационной модели процесса функционирования конвертерного производства металлургического комбината с двумя сталеплавильными цехами, включающими, соответственно, два и три конвертера [3 – 5]. Наличие такой модели позволит найти комплексное решение исследуемых задач.
Эволюция представлений об имитационных моделях
и современные требования к ним
Базовое представление имитационной модели создано для промышленных изделий, где имела место четкая связь имитационной модели с изделием на всех стадиях его жизненного цикла от создания до утилизации. По мере развития этот подход был распространен на производственные процессы [6 – 8]. Развитие представлений об имитационной модели, согласно приведенной в работе [3] схеме, проходит четыре стадии:
1 – физические объекты (изделия) создаются без имитационной модели (без цифрового прототипа);
2 – имитационная модель (цифровой прототип) используется только на стадии создания изделия;
3 – присутствует информационный обмен между физическим объектом и цифровой моделью;
4 – физический объект и цифровая модель взаимодействуют в реальном времени, обеспечивая информацией процессы совершенствования как физического объекта, так и цифровой модели.
Концепция взаимодействия физического изделия (процесса) реального мира и его цифровой модели виртуального пространства, а также наличие информационной связи между ними, объединяющей виртуальный и материальный миры, отображает идею цифрового двойника [9 – 11].
В соответствии с приведенным описанием стадий эволюции цифровых моделей перед исследователями стоит задача построения цифровой модели процесса функционирования конвертерного производства металлургического комбината, соответствующей третьей стадии. На современном этапе общепринятые требования к функционалу цифровой модели исследуемого процесса функционирования конвертерного производства включают:
– отражение структуры производства, производительности и технического состояния агрегатов, длительности кампаний конвертеров, длительности ремонтных периодов и др.;
– применение различных механизмов управления для решения задач распределения входного потока чугуна между конвертерными цехами для формирования календарных графиков работы отдельных конвертеров и их ремонтов;
– накапливание информации по мере использования модели для целей оптимизации и прогнозирования результатов процесса функционирования;
– сбор данных о процессе функционирования конвертерного производства и применение инструментов предиктивной аналитики для планирования работы и ремонтов конвертеров;
– формирование данных, которые невозможно получить непосредственно на физическом объекте и которые могут быть использованы для оптимизации параметров процесса функционирования конвертерного производства;
– визуализацию результатов процесса функционирования цифровой модели [12 – 14].
Виртуальную часть цифрового двойника представляют в виде двух составляющих: цифрового мастера и цифровой тени. Цифровой мастер содержит информацию, достаточную для построения моделируемого процесса. Цифровая тень – это набор данных, которые функционирующий физический объект (процесс) «отбрасывает» в виртуальное пространство, и модели, позволяющие прогнозировать свойства процесса в определенных пределах [15 – 17].
Элементы формализованного описания процесса функционирования конвертерного производства
Основные понятия и обозначения. Обозначим через O = {OI , OII } сталеплавильное производство, включающее два цеха. Причем OI = {o1 , o2 , o3 } и OII = {o4 , o5 }, то есть в первом цехе функционирует три конвертера одного типоразмера, а во втором – два однотипных агрегата. В качестве интервала исследуемых задач планирования выберем последовательность (T1 , T2 , …, Tj , …, Tp ) из p месяцев, \({T_j} = (\Delta {t_l}|l = {\overline {1,L} _j})\) (где Lj – количество суток в j-ом месяце). Причем каждый конвертер представляет собой дискретный агрегат циклического действия. При описании конвертера кортеж oi = o( fi , ρi , gi , Ki , \(k_{ij}^b\), ri ), (где fi – производство стали, выплавленной агрегатом за один цикл, т; ρi – расходный коэффициент, описывающий потребность в чугуне gi для выплавки одной тонны стали (gi = fiρi , ρ < 1); Ki – нормативная длительность кампании конвертера (количество плавок, которые должен провести агрегат на одной футеровке от одного холодного ремонта до последующего); \(k_{ij}^b\) – количество плавок, выплавленных i-ым конвертером на начало j-го периода планирования; riν , \(\nu = \overline {1,2,...} \) – длительности (в сутках) остановок (ремонт/ожидание) i-го конвертера. Тогда в силу однотипности конвертеров в каждом цехе можно представить равенства:
| \[\begin{array}{c}{f_i} = {f_I},{\rm{ }}i = \overline {1,3} {\rm{; }}{\rho _i} = {\rho _I}, i = \overline {1,3} {\rm{; }}\\{g_i} = {g_I}; {K_i} = {K_I},{\rm{ }}i = \overline {1,3} ;\end{array}\] | (1) |
| \[\begin{array}{c}{f_i} = {f_{II}}, i = \overline {4,5} {\rm{; }}{\rho _i} = {\rho _{II}}, i = \overline {4,5} {\rm{; }}\\{g_i} = {g_{II}};{K_i} = {K_{II}},{\rm{ }}i = \overline {4,5} .\end{array}\] | (2) |
Обозначим через mij (Δtl ), mIj (Δtl ), mIIj (Δtl ) количество плавок, выпускаемых конвертером i, цехами OI и OII соответственно в l-ые сутки j-го периода. Очевидно, что
| \[\begin{array}{c}\sum\limits_{i = 1}^3 {{m_{ij}}(\Delta {t_l})} = {m_{Ij}}(\Delta {t_l});\\\sum\limits_{i = 4}^5 {{m_{ij}}(\Delta {t_l})} = {m_{IIj}}(\Delta {t_l}).\end{array}\] | (3) |
Под календарным планом работы i-го конвертера в j-ом месяце будем понимать последовательность
| \[({m_{ij}}(\Delta {t_l})|l = {\overrightarrow {1,L} _j}).\] | (4) |
Если l является днем ремонта конвертера или нахождения его в резерве, то mij(Δtl ) = 0.
Введем функцию kij(l), описывающую количество плавок, выпущенных i-ым конвертером от начала кампании до l-ых суток j-го периода включительно. Значения данной функции будут ограничены величинами нормативной длительности кампаний конвертеров
| \[{k_{ij}}(l) \le \left\{ {\begin{array}{*{20}{c}}{{K_I},{\rm{ }}i = \overline {1,3,} }\\{{K_{II}},{\rm{ }}i = \overline {4,5.} }\end{array}} \right.\] | (5) |
Обозначим через \(k_{ij}^b\) количество плавок, проведенных i-ым конвертером на начало j-го периода планирования. Тогда, с учетом условия (4), количество плавок \(k_{ij}^e\), выпущенных i-ым конвертером на конец j-го планового периода, можно представить как
| \[k_{ij}^e = k_{ij}^b + \sum\limits_{l = 1}^{{S_j}} {{m_i}\left( {\Delta {t_{{s_j}}}} \right)} ,\] | (6) |
при этом \(k_{ij}^e = k_{ij + 1}^n.\)
Структурные ограничения на функционирование конвертеров в цехах. При реализации конвертером календарного плана работы (4), значение функции будет возрастать на величину mij(Δtl ) каждые последующие сутки [kij(l) = kij (l – 1) + mij(Δtl )], пока ее значение не достигнет величины нормативной длительности кампании конвертера. Функция kij(l) имеет «пилообразный» вид, размер основания «зуба пилы» зависит от календарного плана работы конвертера и может охватывать несколько периодов планирования. При достижении максимума функция сохраняет это значение до окончания ремонта конвертера. При выходе из ремонта (нахождении конвертера в резерве) функция равна нулю. Колебания функции kij(l) являются регулярными, но не имеют фиксированного периода.
Рис. 1. Проектная схема работы конвертеров первого цеха |
Проектные решения для первого цеха предписывают схему работы конвертеров, представленную на рис. 1. Эта схема не допускает одновременной работы трех конвертеров, а предполагает постоянную работу двух агрегатов при условии, что третий находится на ремонте или в резерве. Определим состояние sij (l) i-го конвертера первого цеха в l-ые сутки j-го периода следующим образом:
| \[{s_{ij}}(l) = \left\{ {\begin{array}{*{20}{c}}{wr,{\rm{ }}0 \le {k_{ij}}(l) \le K;}\\{rm,{\rm{ }}{k_{ij}}(l) = K;}\\{rz,{\rm{ }}{k_{ij}}(l) = 0.}\end{array}} \right.\] | (7) |
Описание смены состояний конвертеров при работе на интервале времени от l(r11 ) до l(r31 ) (рис. 1) показано в таблице.
Порядок работы конвертеров цеха 1
| |||||||||||||||||
Проектные решения и система организации ремонтов во втором цехе не допускают выполнения в одном плановом периоде более одного холодного ремонта. На рис. 2 представлены допустимая и недопустимая схемы работы конвертеров второго цеха.
Рис. 2. Допустимая (а) и недопустимая (б) схемы работы |
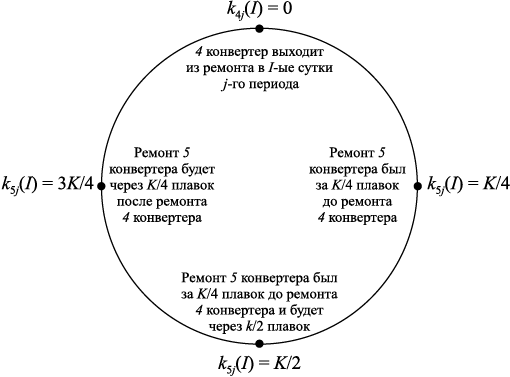
Заметим, что для максимальной удаленности ремонтов конвертеров 4 и 5, выраженной в количестве выпускаемых плавок, абсолютная разность значений функций k4 (l) и k5 (l) должна быть максимально возможной. Максимум абсолютной разности функций k4 (l) и k5 (l) составляет величину K/2 (рис. 3). Это условие максимальной удаленности имеет место и для первого цеха, так как согласно проектной схеме работы конвертеров в каждые сутки работают два агрегата из трех.
Рис. 3. Зависимость абсолютной разности |k4(l) – k5(l)| |
Количественные ограничения на работу конвертеров. На совместную работу агрегатов в цехах накладываются технологические ограничения, определяющие диапазон изменения количества плавок в сутки в каждом цехе при одном или двух одновременно работающих конвертерах:
| \[\underline {m_I^1} \le {m_{ij}}(\Delta {t_l}) \le \overrightarrow {m_I^1} ,{\rm{ }}i = {\rm{ }}\overline {1,3} ,{\rm{ }}j = \overrightarrow { 1,P} ;\] | (8) |
| \[\underline {m_{II}^1} \le {m_{ij}}(\Delta {t_l}) \le \overrightarrow {m_{II}^1} ,{\rm{ }}i = \overline {4,5} ,{\rm{ }}j = \overrightarrow {1,P} ;\] | (9) |
| \[\begin{array}{c}2\underline {m_I^1} \le \left[ {{m_{ij}}(\Delta {t_l}) + {m_{i'j}}(\Delta {t_l})} \right] \le \overline {2m_I^1} ;{\rm{ }}\\i \ne i',{\rm{ }}i,{\rm{ }}i' = \overline {1,3} ,{\rm{ }}j = \overrightarrow {1,P} ;\end{array}\] | (10) |
| \[2\underline {m_{II}^1} \le \left[ {{m_{4j}}(\Delta {t_l}) + {m_{5j}}(\Delta {t_l})} \right] \le \overline {2m_{II}^1} ,{\rm{ }}j = \overrightarrow {1,P} ,\] | (11) |
здесь \(\underline {m_I^1} \), \(\overrightarrow {m_I^1} \), \(\underline {m_{II}^1} \), \(\overrightarrow {m_{II}^1} \), 2\(\underline {m_I^1} \), 2\(\overrightarrow {m_I^1} \), 2\(\underline {m_{II}^1} \), 2\(\overrightarrow {m_{II}^1} \) – минимальное и максимальное количество плавок, выпускаемых в первом и втором цехах при работе одним конвертером, а также минимальное и максимальное количество плавок, выпускаемых в цехах при работе двумя конвертерами соответственно. Заметим, что 2\(\underline {m_I^1} \) < \(\overrightarrow {m_I^1} \) и 2\(\underline {m_{II}^1} \) < \(\overrightarrow {m_{II}^1} \), так как в противном случае количества плавок в диапазонах от \(\overrightarrow {m_I^1} \) до 2\(\underline {m_I^1} \) и от \(\overrightarrow {m_{II}^1} \) до 2\(\underline {m_{II}^1} \) цех не может произвести, что не соответствует действительности. Работа тремя конвертерами в первом цехе технологически не реализуема.
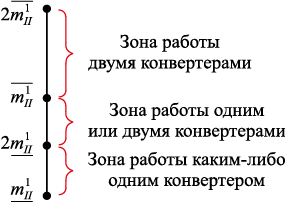
Таким образом, первый цех, который, согласно проектным решениям, должен постоянно работать двумя конвертерами, может производить от 2\(\underline {m_I^1} \) до 2\(\underline {m_{II}^1} \) плавок, причем каждый из агрегатов может выпускать от \(\underline {m_I^1} \) до \(\overrightarrow {m_I^1} \) плавок. Второй цех в диапазоне от \(\underline {m_{II}^1} \) до 2\(\underline {m_{II}^1} \) плавок может работать только одним конвертером (режим работы 1), в диапазоне от 2\(\underline {m_{II}^1} \) до \(\overrightarrow {m_{II}^1} \) – как одним, так и двумя конвертерами (режим работы 2), а в диапазоне от \(\overrightarrow {m_{II}^1} \) до 2\(\overrightarrow {m_{II}^1} \) – только двумя конвертерами (режим работы 3) (рис. 4).
Рис. 4. Диапазоны режимов работы конвертеров второго цеха |
Определение объемов суточного необходимого производства чугуна доменным цехом. Чугун, являющийся основной составляющей металлозавалки конвертеров, производится тремя доменными печами (агрегатами непрерывного действия). Будем описывать каждую доменную печь объемами среднесуточного производства чугуна gq(Δt) на полном ходу (зависит от объема доменной печи), объемом gq(Δt)/2 производства на тихом ходу (при возможном выполнении планово-предупредительных ремонтов), графиком \(\left[ {{r_q}{\rm{ = }}\Delta {t_l}{\rm{| }}l {\rm{ = }}\left( {\overline {l_{qj}^b,l_{qj'}^e} } \right)} \right]\) ее капитального ремонта (выполняется раз в 4 – 5 лет), а также графиком \(r_{qj}^{{\rm{ппр}}} = (l_{qj}^1,{\rm{ }}..,{\rm{ }}l_{qj}^\nu ),\) планово-предупредительных ремонтов в j-ом периоде, длительность которых, как правило, не превышает 12 ч (здесь \(q = \overline {1,3} \) – номер доменной печи; \(l_{qj}^b,{\rm{ }}l_{qj'}^e\) – сутки начала и окончания капитального ремонта соответственно; ν – количество планово-предупредительных ремонтов в j-ом периоде).
Обозначим через gqj (Δtl ) планируемое производство чугуна для q-ой доменной печи в l-ые сутки j-ого периода
| \[{g_{qj}}(\Delta {t_l}) = \left\{ {\begin{array}{*{20}{c}}{{g_q}(\Delta t),{\rm{ }}l \notin (\overline {l_{qj}^b,{\rm{ }}l_{q{j^/}}^e} );}\\{0,{\rm{ }}l \in (\overline {l_{qj}^b,{\rm{ }}l_{q{j^/}}^e} );}\\{\frac{{{g_q}(\Delta t)}}{2},{\rm{ }}l \in (l_{qj}^1,{\rm{ }}..,{\rm{ }}l_{qj}^\nu ).}\end{array}} \right.\] | (12) |
Очевидно, общий объем производства чугуна в l-ые сутки составит
| \[{g_j}(\Delta {t_l}) = \sum\limits_{q = 1}^3 {{g_{qj}}(\Delta {t_l})} ,{\rm{ }}l = \overline {1,{L_j}} .\] | (13) |
Последовательность \(\left( {{g_j}(\Delta {t_l})|l = \overline {1,{L_j}} } \right)\) описывает планируемое посуточное производство чугуна доменным цехом в j-ом периоде. При календарном плане работы конвертеров, задаваемым соотношением (4), должны иметь место равенства
| \[{g_I}\sum\limits_{i = 1}^3 {{m_{ij}}(\Delta {t_l}) + {\rm{ }}} {g_{II}}\sum\limits_{i = 4}^5 {{m_{ij}}(\Delta {t_l}) = {g_j}(\Delta {t_l}),{\rm{ }}l = \overline {1,{L_j}} } .\] | (14) |
Особенности задач исследования и подход к их решению
В состав основных прикладных задач, требующих решения с учетом изложенных выше модельных представлений об объекте исследования, входят:
1. формирование графиков \(\left( {{m_{Ij}}(\Delta {t_l})|l = \overline {1,{L_j}} } \right),{\rm{ }}\left( {{m_{IIj}}(\Delta {t_l})|l = \overline {1,{L_j}} } \right)\) выпуска плавок конвертерными цехами на основе графика \(\left( {{g_j}(\Delta {t_l})|l = \overline {1,{L_j}} } \right)\) производства чугуна для каждого периода j с целью определения месячных плановых заданий цехам;
2. формирование графиков ремонта конвертеров в цехах производства
| \[\begin{array}{c}{\left( {l_{ij}^n,{\rm{ }}l_{ij'}^e} \right)_\nu } \subset \bigcup\limits_{j = 1}^P {{T_j}} ,{\rm{ }}i = {\rm{ }}\overrightarrow {1,5} ,{\rm{ }}\nu = \overline {1,2,...} ,{\rm{ }}\\{r_\nu } = \left\{ {\begin{array}{*{20}{c}}{l_{ij'}^e - l_{ij}^n,{\rm{ }}j = j';{\rm{ }}}\\{{L_j} - l_{ij}^n + l_{ij'}^e,{\rm{ }}j \ne j'}\end{array}} \right.\end{array}\] | (15) |
с целью планирования работы ремонтных служб металлургического комбината;
3. формирование графиков \(\left[ {({m_{ij}}(\Delta {t_l})|l = {{\overrightarrow {1,L} }_j})|i = \overline {1,3} } \right]\) и \(\left[ {({m_{ij}}(\Delta {t_l})|l = {{\overrightarrow {1,L} }_j})|i = \overline {4,5} } \right]\) работы конвертерных цехов с целью переработки цехами поступающего из доменного цеха жидкого чугуна.
Таким образом, к основным особенностям исследуемых задач можно отнести дискретность и нелинейность функций, функционалов, операторов, параметров и критериев, описывающих задачи. В частности, в соответствии с рис. 3, одним из предпочтительных при календарном планировании может быть критерий
| \[\begin{array}{c}Q = \sum\limits_{j = 1}^P {\left[ {\left( {\left| {k_{ij}^e - k_{i'j}^e} \right| - 0,5{K_1}} \right)} \right. + } \\\left. { + \left( {\left| {k_{4j}^e - k_{5j}^e} \right| - 0,5{K_{II}}} \right)} \right] \to \min ,\end{array}\] | (16) |
направленный на обеспечение максимальной удаленности ремонтов двух работающих конвертеров (выраженной в количестве выпускаемых плавок). Функционал Q относится к классу дискретных и нелинейных. Дискретность и нелинейность задач затрудняют и делают невозможным построение соответствующих аналитических моделей, позволяющих определять и ранжировать множество допустимых решений.
Таким образом, формализация исследуемых задач показывает, что особенности процесса функционирования конвертерного производства делают затруднительным (или практически невозможным) построение и использование аналитических решений. С учетом этих обстоятельств авторами выбран подход к решению поставленных задач, базирующийся на создании и использовании цифровой дискретно-событийной имитационной модели, которая:
– представляет собой цифровую копию исследуемого процесса функционирования конвертерного производства, отражает его структуру, производительность, техническое состояние и такие параметры, как длительность кампании конвертеров, длительность ремонтных периодов и др.;
– использует различные механизмы управления для решения задач распределения входного потока чугуна между конвертерными цехами, формирования календарных графиков работы отдельных конвертеров и их ремонтов;
– накапливает информацию по мере ее функционирования для целей оптимизации и прогнозирования результатов процесса функционирования;
– позволяет собирать данные о процессе функционирования конвертерного производства и использовать инструменты предиктивной аналитики для планирования ремонтов;
– предоставляет данные, которые невозможно получить непосредственно на физическом объекте и которые могут быть использованы для оптимизации параметров системы;
– формирует наборы данных для визуализации отдельных результатов процесса функционирования [18 – 20].
Выводы
Показаны существенная взаимозависимость, дискретность и нелинейность задач планирования объемов производства, ремонтов и графиков работы конвертеров и обоснована необходимость создания цифровой дискретно-событийной имитационной модели процесса функционирования конвертерного производства металлургического комбината для численного решения исследуемых задач путем компьютерного моделирования.
Список литературы
1. Лэсдон Л. Оптимизация больших систем. Москва: Наука; 1975:432.
2. Hamann-Lohmer J., Lasch R. Production planning and scheduling in multi-factory production networks: A systematic literature review. International Journal of Production Research. 2021;59(7):2028–2054. https://doi.org/10.1080/00207543.2020.1797207
3. Прохоров А., Лысачев М. Цифровой двойник. Анализ, тренды, мировой опыт / Научн. ред. проф. А.И. Боровков. Издание первое, исправленное и дополненное. Москва: ООО «АльянсПринт»; 2020:401.
4. Glaessgen E.H., Stargel D.S. The digital twin paradigm for future NASA and U.S. air force vehicles. In: 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conf. 20th AI. 23–26 April 2012, Honolulu, Hawaii. https://doi.org/10.2514/6.2012-1818
5. The new age of manufacturing: Digital twin technology & IoT [Electronic resource]. URL: http://www.innovation4.cn/library/r46394/. (Accessed: 20.01.2025).
6. Modern manufacturing’s triple play: Digital twins, analytics and the internet of things [Electronic resource]. URL: https://www.nextspace.com/recommended-reading/modern-manufacturings-triple-play-digital-twins-analytics-and-iot. (Accessed: 20.01.2025).
7. Цифровые двойники в ритейле – кто это такие и почему с ними срочно нужно знакомиться? [Электронный ресурс]. URL: https://new-retail.ru/tehnologii/tsifrovye_dvoyniki_v_riteyle_kto_eto_takie_i_pochemu_s_nimi_srochno_nuzhno_znakomitsya5533/?ysclid=m8ajyzvqlj502045804. (Дата обращения: 20.01.2025).
8. «15 ключевых компонентов современного производства» (Сайт Nanonews.net) [Электронный ресурс]. URL: https://www.nanonewsnet.ru/articles/2017/15-klyuchevykh-komponentov-sovremennogo-proizvodstva. (Дата обращения: 20.01.2025).
9. Цифровые двойники и цифровые тени в высокотехнологичной промышленности [Электронный ресурс]. URL: https://4science.ru/articles/Cifrovie-dvoiniki-i-cifrovie-teni-v-visokotehnologichnoi-promishlennosti. (Дата обращения: 20.01.2025).
10. Ключевые инструменты и форматы развития цифровой экономики: «умные» цифровые двойники и Центр НТИ СПбПУ [Электронный ресурс]. URL: https://nticenter.spbstu.ru/news/6722. (Дата обращения: 20.01.2025).
11. UK team to develop rapid virtual testing technique for manufactured components [Electronic resource]. URL: https://www.theengineer.co.uk/content/news/uk-team-to-develop-rapid-virtual-testing-technique-for-manufactured-components/. (Accessed: 20.01.2025).
12. Боровков А.И., Рябов Ю.А. Определение, разработка и применение цифровых двойников: подход Центра компетенций НТИ СПбПУ «Новые производственные технологии». Цифровая подстанция. 2019;(12):20–25.
13. Design with Confidence (Commentary). CIMdata [Electronic resource]. URL: https://www.cimdata.com/de/resources/complimentary-reports-research/commentaries/item/3345-design-with-confidence-commentary/3345-design-with-confidence-commentary. (Accessed: 20.01.2025).
14. Rodič B. Industry 4.0 and the new simulation modelling paradigm. Organizacija. 2017;50(3):193–207. https://doi.org/10.1515/orga-2017-0017
15. Mukherjee T., DebRoy T. A digital twin for rapid qualification of 3D printed metallic components. Applied Materials Today. 2019;14:59–65. https://doi.org/10.1016/j.apmt.2018.11.003
16. Lind M. Digital thread. Aras [Electronic resource]. URL: https://community.aras.com/b/english/posts/promise-of-the-digital-thread. (Accessed: 28.05.2020)
17. Новая парадигма цифрового проектирования и моделирования глобально конкурентоспособной продукции нового поколения [Электронный ресурс]. URL: http://fea.ru/news/6721. (Дата обращения: 20.01.2025).
18. Прохоров И.М., Зимин А.В., Буркова И.В., Зимин В.В. Постановка и декомпозиция задачи календарного планирования ремонтов и работы конвертеров сталеплавильного производства. Системы управления и информационные технологии. 2024;(2(96)):38–40.
19. Корнет М.Е., Зимин А.В., Буркова И.В., Зимин В.В. Планирование системы ремонтов конвертеров в условиях квазипериодического функционирования агрегатов. Известия вузов. Черная металлургия. 2024;67(6):738–743. https://doi.org/10.17073/0368-0797-2024-6-738-743
20. Прохоров И.М., Зимин А.В., Буркова И.В., Зимин В.В. О процедуре решения задачи построения расписания ремонтов конвертеров сталеплавильного цеха с двумя агрегатами. Системы управления и информационные технологии. 2024;(2(96)):64–67.
Об авторах
А. В. ЗиминРоссия
Алексей Валерьевич Зимин, д.т.н., доцент, заведующий кафедрой автоматизации и информационных систем
Россия, 654007, Кемеровская область – Кузбасс, Новокузнецк, ул. Кирова, 42
М. Е. Корнет
Россия
Мария Евгеньевна Корнет, старший преподаватель кафедры инженерной кибернетики
Россия, 119049, Москва, Ленинский пр., 4
И. В. Буркова
Россия
Ирина Владимировна Буркова, д.т.н., доцент, ведущий научный сотрудник
Россия, 117997, Москва, ул. Профсоюзная, 65
В. В. Зимин
Россия
Валерий Викторович Зимин, д.т.н., профессор кафедры автоматизации и информационных систем
Россия, 654007, Кемеровская область – Кузбасс, Новокузнецк, ул. Кирова, 42
Рецензия
Для цитирования:
Зимин А.В., Корнет М.Е., Буркова И.В., Зимин В.В. Использование цифровых имитационных моделей для оптимизации работы сложных производственных объектов. Известия высших учебных заведений. Черная Металлургия. 2025;68(2):188-194. https://doi.org/10.17073/0368-0797-2025-2-188-194
For citation:
Zimin A.V., Kornet M.Е., Burkova I.V., Zimin V.V. Using digital simulation models to optimize the operation of complex production facilities. Izvestiya. Ferrous Metallurgy. 2025;68(2):188-194. https://doi.org/10.17073/0368-0797-2025-2-188-194
JATS XML