Scroll to:
Development of models for functioning of drawing equipment for multi-mill servicing
https://doi.org/10.17073/0368-0797-2025-1-84-89
Abstract
The great demand for products of the drawing industry causes the need to increase the productivity of existing equipment. There are two ways to solve this issue: creation of new designs of drawing equipment and search for hidden organizational reserves. Increasing productivity through organizational measures requires less time and material costs for implementation. The paper considers the possibility and prospects of multi-mill servicing. Normative models of drawing equipment operation for multi-mill servicing were developed. The prospects of using the developed models are shown on the example of the existing production. Analysis of the drawing equipment operation made it possible to justify the processing modes for multi-mill servicing and thereby increase productivity by 1.35 times and reduce the cost of finished products by 2 %.
For citations:
Fastykovskii A.R., Musatova A.I., Martyushev N.V. Development of models for functioning of drawing equipment for multi-mill servicing. Izvestiya. Ferrous Metallurgy. 2025;68(1):84-89. https://doi.org/10.17073/0368-0797-2025-1-84-89
Introduction
The analysis of the established regulatory framework for performance indicators within the drawing mill–wire drawer system, which includes the duration of operations (machine-based, machine-assisted manual, and manual), situational operational cycles of the mills, their utilization factors, downtime, and system productivity, has enabled the optimization of the number of drawing mills that a single operator can effectively service [1 ‒ 3].
To achieve this, a standard model for the operation of the human-technical system in a multi-mill servicing mode was developed [4 ‒ 6]. Initially, drawing mills operating in rough, intermediate, and fine wire drawing sections (over 50 units in total) were grouped according to the degree of drawing reduction (ranging from single-pass to seven-pass processes), the diameters of the drawn wire, and the final drum size (750, 650, 550, or 350 mm). In single-pass drawing mills, the process involves a single die, with the wire undergoing one reduction in cross-section. In multi-pass drawing mills of the magazine-type, block machines are installed, consisting of multiple blocks with individual drive mechanisms for each drum, where the wire stock sequentially passes through multiple dies. Each mill is equipped with pay-off and take-up devices, an overhead crane, welding and pointing machines.
Rough and intermediate (single-pass and multi-pass) drawing mills are designed to produce wire with diameters ranging from 8 to 2 mm, wound into small bundles (SB) weighing 100 – 250 kg, heavy bundles (HB) weighing 1.0 or 1.5 tons, or coils (C) weighing 1.0 ton, depending on the type of mill. The initial stock wire for these mills consists of rod coils (RC) with diameters ranging from 10 to 5 mm. Fine (seven-pass) drawing mills (7/350) are used for producing wire with diameters from 2.0 to 0.8 mm, either in bundles (60 kg) or coils (1.0 ton), depending on the intended application.
Each group of drawing mills was classified based on the following criteria: type of pay-off device (horizontal or vertical); type of take-up device (for forming wire onto coils or heavy bundles); method of small bundle removal (cantilever rotating crane or continuous removal installation); form of the initial stock wire (rod coil or coil); type and weight of finished products (small and heavy bundles, coils); diameter and regulatory standard (GOST) of the finished wire; spatial arrangement of drawing mills, including distances between them and their control panels.
To determine the feasibility of a single wire drawer servicing two or more mills, comprehensive studies were conducted on the drawing mill–wire drawer system using time-lapse photography and chronometric observations over the course of 30 work shifts.
Development of a standard model for system operation
The standard model for determining the feasibility of an operator servicing multiple drawing mills includes the following parameters [7 ‒ 9].
1. Time spent by the operator servicing a single drawing mill:
| \[{\rm{\tau }}_{{\rm{w}}N}^{\rm{s}}(i) = \sum\limits_{n = 1}^{n*} {{\rm{\tau }}_{{\rm{m}}{\rm{,}}n}^{\rm{s}}(i)} + \sum\limits_{z = 1}^{z*} {{\rm{\tau }}_{{\rm{ov}},z}^{\rm{s}}(i)} + {\rm{\tau }}_{{\rm{a}}N}^{\rm{s}}(i);\] | (1) |
| \[\tau _{{\rm{m}}{\rm{,}}}^{\rm{s}}(i) = \frac{{\tau _{{\rm{m}}{\rm{,}}}^{{\rm{mp}}}(i)}}{{k_{{\rm{m}}{\rm{,}}}^{\rm{s}}(i)}};{\rm{ \tau }}_{{\rm{ov}},z}^{\rm{s}}(i) = \frac{{{\rm{\tau }}_{{\rm{ov}},z}^{{\rm{mp}}}(i)}}{{k_{{\rm{ov}},z}^{\rm{s}}(i)}};\] | (2) |
| \[{\rm{\tau }}_{{\rm{a}}N}^{\rm{s}}(i) = t_{{\rm{m}}N}^{\rm{s}}(i){k_{\rm{a}}};{\rm{ }}t_{{\rm{m}}N}^{\rm{s}}(i) = \frac{{{t_{{\rm{m}}N}}(i)}}{{k_{\rm{о}}^{\rm{s}}(i)}},\] | (3) |
where \({\rm{\tau }}_{{\rm{m}}{\rm{,}}n}^{\rm{s}}\)(i) and \({\rm{\tau }}_{{\rm{m}}{\rm{,}}n}^{\rm{mp}}\)(i) – the standard and minimum possible time required for the operator to perform the n-th cyclic operation (or its elements) when manufacturing one unit of the i-th product, not overlapped by machine drawing time, h; \({\rm{\tau }}_{{\rm{ov}}{\rm{,}}z}^{\rm{s}}\)(i) and \({\rm{\tau }}_{{\rm{ov}}{\rm{,}}z}^{\rm{mp}}\)(i) – the standard and minimum possible time required for the operator to perform the n-th cyclic operation (or its elements) when manufacturing one unit of the i-th product, overlapped by machine drawing time, h; \(k_{{\rm{m}},n}^{\rm{s}}\) (i) and \(k_{{\rm{ov}},z}^{\rm{s}}\) (i) – the standard instability coefficients for manual operations and their elements, considering both overlapped and non-overlapped machine drawing times; \({\rm{\tau }}_{{\rm{a}}N}^{\rm{s}}\) (i) – the standard time for active observation of the drawing process by the operator, h; \(t_{{\rm{m}}N}^{\rm{s}}\)(i) and tmN (i) – the standard and technically possible machine time for drawing wire of the i-th diameter at the N-th drawing speed, h; ka – the regulated active observation coefficient (ka = 0.1 ÷ 0.2); \(k_{\rm{o}}^{\rm{s}}\) – the standard equipment (mill) utilization coefficient.
2. Planned machine-free idle time of the operator:
| \[t_{{\rm{mf}}N}^{\rm{s}}(i) = t_{{\rm{m}}N}^{\rm{s}}(i) - \left[ {\sum\limits_{z = 1}^{z*} {\tau _{{\rm{ov}},z}^{\rm{s}}} (i{\rm{)}} + \tau _{\rm{a}}^{\rm{s}}(i)} \right].\] | (4) |
3. Planned operator workload time when servicing S identical drawing mills:
| \[{\rm{\tau }}_{{\rm{w}}N}^{\rm{s}}(S{\rm{, }}i) = {\rm{\tau }}_{{\rm{w}}N}^{\rm{s}}(i) + {\rm{\tau }}_{tx}^{\rm{s}}(S{\rm{, }}i);\] | (5) |
| \[{\rm{\tau }}_{tx}^{\rm{s}}(S,{\rm{ }}i) = \frac{{{\rm{\tau }}_{tx}^{{\rm{mp}}}(S{\rm{, }}i)}}{{k_{{\rm{ins}}}^{\rm{s}}(S{\rm{, }}i)}},\] | (6) |
where \({\rm{\tau }}_{{\rm{t}}x}^{\rm{s}}\) (S, i) and \({\rm{\tau }}_{{\rm{t}}x}^{\rm{mp}}\) (S, i) – the standard and minimum possible duration of the operator’s transition from one mill to another, h; \(k_{{\rm{ins}}}^{\rm{s}}\)(S, i) – the standard coefficient accounting for instability in the operator’s transition route.
4. Standard transition time for the operator moving between mills, determined through simulation modeling of operator actions while servicing S mills, considering optimal routing and the number of transitions depending on the weight and type of products.
5. Planned operator idle time during the drawing process when servicing S mills
| \[t_{{\rm{mf}}N}^{\rm{s}}{\rm{(}}S{\rm{, }}i{\rm{)}} = t_{{\rm{mf}}N}^{\rm{s}}{\rm{(}}i{\rm{)}} - \tau _{{\rm{t}}x}^{\rm{s}}{\rm{(}}S{\rm{, }}i{\rm{)}}.\] | (7) |
6. Planned operational time of the operator
| \[t_{{\rm{op}},N}^{\rm{s}}{\rm{(}}S{\rm{, }}i{\rm{)}} = t_{{\rm{mf}}N}^{\rm{s}}{\rm{(}}i{\rm{)}} + \tau _{{\rm{w}}N}^{\rm{s}}{\rm{(}}S{\rm{, }}i{\rm{)}}.\] | (8) |
7. Operator workload coefficient
| \[{k_{{\rm{w}},N}}(S,{\rm{ }}i) = \frac{{{\rm{\tau }}_{{\rm{w}}N}^{\rm{s}}(S,{\rm{ }}i)}}{{t_{{\rm{op}},N}^{\rm{s}}(S,{\rm{ }}i)}} \le k_{\rm{w}}^*(i);{\rm{ }}k_{\rm{w}}^*(i) \in (0.4 \div 0.7).\] | (9) |
8. Planned number of drawing mills to be serviced by a single operator
| \[{S_N}(i) = \left[ {\frac{{t_{{\rm{mf}}N}^{\rm{s}}(S{\rm{, }}i)}}{{{\rm{\tau }}_{{\rm{w}}N}^{\rm{s}}(S{\rm{, }}i)}} + 1} \right]{k^{\rm{s}}},\] | (10) |
where ks is the overall coefficient accounting for downtime in multi-mill servicing with S mills.
9. Operator’s production rate in multi-mill servicing
| \[\begin{array}{c}{H_{{\rm{hts}}{\rm{, }}N}}(S,{\rm{ }}i) = P_{{\rm{hts }},N}^{\rm{s}}(i) \times \\ \times S_N^{\rm{s}}(i)\;{\rm{ФВ}}_{{\rm{hts}}{\rm{, sh}}}^{\rm{s}}(S,{\rm{ }}i){\rm{, t/shift}};\end{array}\] | (11) |
| \[\begin{array}{c}{\rm{ФВ}}_{{\rm{hts}}}^{\rm{s}}(S,{\rm{ }}i) = {\rm{К}}{{\rm{В}}_{{\rm{sh}}}} - \\ - \left[ {\sum\limits_{{\rm{m}} = 1}^{\rm{m}} {{t_{{\rm{reg}}}} + t_{\rm{tec}}^{\rm{s}}(i) + t_{{\rm{tch}}}^{\rm{s}}(i) + t_{{\rm{cns}}}^{\rm{s}}(i) + t_{{\rm{org}}}^{\rm{s}}(i)} } \right]{\rm{,}}\end{array}\] | (12) |
where \(P_{{\rm{hts}},N}^{\rm{s}}\) (i) – the standard productivity of an identical human-technical system, t/h; \(\Phi {\rm B}_{{\rm{hts}}{\rm{, sh}}}^{\rm{s}}\)(S, i) – the standard working time fund of the human-technical system, considering regulated operator breaks \(\sum\limits_{{\rm{m}} = 1}^{\rm{m}} {{t_{{\rm{reg}}}}} \) standard downtimes due to coinciding manual operations \(t_{{\rm{cns}}}^{\rm{s}}\) while servicing S mills, standard downtimes due to technical \(t_{{\rm{tec}}}^{\rm{c}}\), technological \(t_{{\rm{tch}}}^{\rm{s}}\) and organizational \(t_{{\rm{org}}}^{\rm{s}}\) reasons, h/shift; \(S_N^{\rm{s}}\) – the standard (assigned) number of mills at the N-th drawing speed.
The standard duration of downtime (stoppages) caused by overlapping operations at adjacent mills was evaluated based on empirically observed patterns: the longer the equipment operates and the fewer manual operations are required, the lower the probability of mill stoppages due to overlapping manual operations.
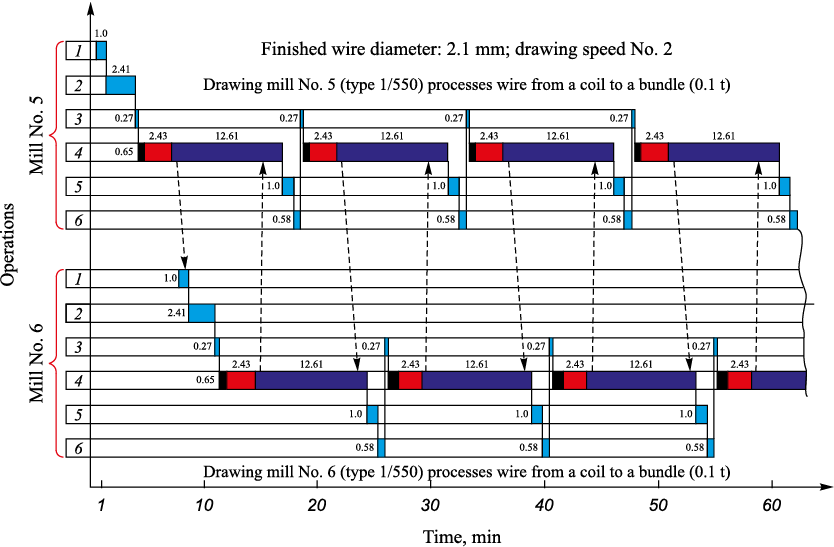
A graphical model of the production process for an operator servicing two drawing mills is schematically presented in the figure. The table provides fragmentary results of system modeling for multi-mill servicing.
Graphical model of the production process during servicing by the operator of two mills (fragment):
Results of modeling the human-technical system in a multi-mill servicing mode
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The calculations, substantiating the number of drawing mills that can be simultaneously serviced by a single operator, were presented to the management of the wire product manufacturing plant. These calculations demonstrated the feasibility and advantages of multi-mill servicing for certain types of mills, with computations conducted for each finished wire diameter, mass, and product form at the second, third, and fourth drawing speeds.
The modeling results for the human-technical system showed that two drawing mills can be operated by a single wire drawer in specific configurations:
1. Mills 6/550, 5/550, 4/550, 3/550 – processing from a rod coil to a coil (or bundle) weighing 1 t;
2. Mills 1/550 – processing from a coil to a bundle (0.1 t) for finished wire diameters of 2.3 – 1.6 mm; mills 1/350 – processing from a coil to a bundle (0.06 t) at the second and third drawing speeds.
The methodology for transitioning from the calculated number of simultaneously serviced mills to the standardized number was developed based on an analysis of technical, organizational, ergonomic, and economic factors [10 – 12].
A standardized approach was established to determine time norms and wire drawer productivity under multi-mill servicing conditions, considering drawing speed, finished wire diameter and type, and the hourly productivity standards for each mill type.
Based on the developed models, measures were proposed for implementing two-mill servicing in the steel wire drawing shop, resulting in notable improvements in technical and economic performance, including a reduction in personnel, a 1.35-fold increase in labor productivity, and a 2 % decrease in production costs.
References
1. Тураев Т.Т., Батиров Я.А., Тожиев Б.А. Модернизация процесса волочения проволочного изделия. Universum: Технические науки: электрон. научн. журн. 2019;3(60). URL: http://7universum.com/ru/tech/archive/item/7049 (дата обращения: 12.12.2024).
2. Baek H.M., Jin Y.G., Hwang S.K., Im Y.-T., Son I.-H., Lee D.-L. Numerical study on the evolution of surface defects in wire drawing. Journal of Materials Processing Technology. 2012;212(4):776–785. https://doi.org/10.1016/j.jmatprotec.2011.10.028
3. Kharitonov V.A., Usanov M.Yu. Improving the methodology for calculating drawing routes for high-carbon steels. Ferrous Metallurgy. Bulletin of Scientific, Technical and Economic Information. 2017;(8):92–95. (In Russ.).
4. Fastykovskii A.R., Chinokalov E.V. Long coiled reinforcement produced by drawing. Steel in Translation. 2019;49(7): 481–483. https://doi.org/10.3103/S0967091219070052
5. Fastykovskii A.R., Martyushev N.V., Musatova A.I., Savchenko I.A., Karlina A.I. Substantiation of normative productivity models of the sheet-rolling shop. Message 1. Chernye metally. 2024;(1):9–16. (In Russ.). https://doi.org/10.17580/chm.2024.01.02
6. Weingartshofer T., Bischof B., Kugi A. Optimization-based path planning framework for industrial manufacturing processes with complex continuous paths. Robotics and Computer-Integrated Manufacturing. 2023;82:102516. https://doi.org/10.1016/j.rcim.2022.102516
7. Loginov Yu.N., Grekhov S.K. Generation of residual stresses in drawing low-carbon steel wire. Stal’. 2021;(5):25–28. (In Russ.)
8. Kuznetsov S.A., Skorodumov I.S., Skorodumova E.A. Dynamic modeling of coarse-medium direct-flow wire drawing on a drawing mill with an automobile transmission as a drive. Globus. 2020;4(50):31–40. (In Russ.). https://doi.org/10.31618/2658-5197-2020-50-4-6
9. Volokitina I., Volokitin A., Panin E., Fedorova T., Lawrinuk D., Kolesnikov A., Yerzhanov A., Gelmanova Z., Liseitsev Y. Improvement of strength and performance properties of copper wire during severe plastic deformation and drawing process. Case Studies in Construction Materials. 2023;19:e02609. https://doi.org/10.1016/j.cscm.2023.e02609
10. Fung K.H., Khairuddin M.H.B., Shamsudin M.F., Ali W.F.F.W., Salleh M.S. Numerical simulation and prediction of stress distribution in multi-pass drawing process of steel rod. AIP Conference Proceedings. 2024;2925(1):020054. https://doi.org/10.1063/5.0185776
11. Emel’yanov A.A., Shil’nikova O.V., Emel’yanova N.Z. Optimization of production programs based on simulation results. Prikladnaya informatika. 2015;10(3(57)):109–121. (In Russ.).
12. Goloviznin S.M., Petrov I.M., Ivantsov A.B. Optimization of wet drawing according to the ratio of breaking stress to draw stress. Izvestiya. Ferrous Metallurgy. 2022;65(9):609–614. (In Russ.). https://doi.org/10.17073/0368-0797-2022-9-609-614
About the Authors
A. R. FastykovskiiRussian Federation
Andrei R. Fastykovskii, Dr. Sci. (Eng.), Assist. Prof., Prof. of the Chair of Metal Forming and Metal Science. OJSC “EVRAZ ZSMK”
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
A. I. Musatova
Russian Federation
Aleksandra I. Musatova, Senior Lecturer of the Chair “Management and Branch Economy”
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
N. V. Martyushev
Russian Federation
Nikita V. Martyushev, Cand. Sci. (Eng.), Assist. Prof. of Department of Information Technology
30 Lenina Ave., Tomsk 634050, Russian Federation
Review
For citations:
Fastykovskii A.R., Musatova A.I., Martyushev N.V. Development of models for functioning of drawing equipment for multi-mill servicing. Izvestiya. Ferrous Metallurgy. 2025;68(1):84-89. https://doi.org/10.17073/0368-0797-2025-1-84-89