Построение поверхности ликвидус пятикомпонентной схемы диаграммы Fe – B – Mn – C – Cr

Введение

Диаграммы состояния сплавов являются технологическим чертежом для теоретиков и практиков в области металлургии, металловедения, обработки металлов давлением, литейного производства, различных областей машиностроения и эксплуатации технических средств.

Принимая во внимание, что большинство используемых сталей и сплавов являются многокомпонентными (n > 3), во многих случаях возникают определенные сложности при определении условий выполнения технологических процессов, фазового состава и свойств сплавов, так как не имеется построенных диаграмм состояния в традиционных координатах температура – концентрация элементов [1 – 3]. Как правило, для описания процессов используют двух- и трехкомпонентные диаграммы, их изотермические сечения, тетраэдры для определенной температуры и/или результаты практических исследований [4 – 6].

В частности, для описания процесса борирования и свойств получаемых слоев нашли применение двух- и трехкомпонентные диаграммы [7 – 9], в которых уточняются концентрации соединений и твердых растворов, температуры превращений, обнаруживаются новые соединения. Определенное значение имеет установленный факт существования борокарбида железа [8; 9]. Он отвечает формуле Fe₂₃(C, B)₆. В других сложных карбидах, встречающихся в сталях, легирующий элемент обычно замещает железо.

Установлено, что при 1000 °C до 80 % углерода в цементите может быть заменено бором и формула принимает вид Fe₃C_0,2B_0,8. В этом случае изменяется период кристаллической решетки: происходит сжатие по осям a и c и расширение вдоль оси b орторомбической решетки. При этом замечено, что с увеличением содержания бора происходит увеличение магнитного момента насыщения и температуры точки Кюри. Этот факт важен при объяснении свойств борированных деталей, в которых под слоем боридов образуются боркарбидные включения [10; 11].

В работе [8] установлено, что борокарбид Fe₂₃(C, B)₆ изоморфен с кубическим карбидом хрома Cr₂₃C₆ (тип структур – d84). При переходе от обогащенного углеродом соединения к обогащенному бором период решетки a изменяется от 1,0594 до 1,0628 нм, а при нагреве от 800 °C Fe₂₃(C, B)₆ плавится конгруэнтно. Из работы, в которой приведены изотермические сечения при температурах 700, 800, 900 и 1000 °C видно, что фаза Fe₂₃(C, B)₆ имеет состав, соответствующий формуле Fe₂₃(C_0,73B_0,27)₆ и она находится в равновесии с бороцементитом Fe₃(C, B) и Fe_α. Фаза Fe₂₃(C_0,44B_0,56)₆ находится в равновесии с Fe₂B и Fe₃(C, B). Из анализа сечения при 800 °C следует, что фаза Fe₂₃(C, B)₆ присутствует в большем диапазоне содержания углерода и бора: между Fe₂₃(C_0,38B_0,62)₆ и Fe₂₃(C_0,77B_0,23)₆ и находится в равновесии с фазами Fe_γ и Fe₃(С, B). Установлено, что борокарбид Fe₂₃(C, B)₆ устойчив до температуры 965 + 5 °C [12 – 14]. Полученные результаты уточняют фазовый состав областей диаграмм и свойства получаемых борированных слоев, так как боркарбидные включения обладают высокой твердостью [15 – 17].

В области поиска решений построения многокомпонентных диаграмм (n > 3) следует отметить термодинамический метод, учитывающий особенности бинарных диаграмм состояния [18]. В частности, построена диаграмма фазового строения четырехкомпонентной системы Fe – Mn – Si – C путем расчета термодинамических констант при температуре фазовых превращений соединений с последующей триангуляцией системы и подсистем. В результате получена диаграмма фазового строения в виде тетраэдра, состоящая из 16 элементарных тетраэдров, содержащих конгруэнтно и инконгруэнтно плавящиеся соединения [19].

Предложенный ранее метод Букке-Шоута [20] приводит к получению тетрады, изображающей состав или состояние системы на плоскости, хотя и исходит из четырехмерной фигуры. Рассмотренные в работах [21; 22] системы создают геометрическое изображение составов многокомпонентных систем на плоскости и мало приемлемы для практического использования. Пути совершенствования общего подхода, рассмотренные в работах [23; 24], способствуют получению не самих рабочих диаграмм, а системы плоских проекций после двойного проектирования, которые также затруднительно использовать в качестве рабочего чертежа при разработке технологических процессов.

При определении температур эвтектических реакций и составов эвтектических сплавов обычно применяли дифференциальную сканирующую калориметрию [25; 26], металлографические исследования [27; 28] и рентгеновскую дифракцию [29]. Эти методы достаточно трудоемки, поэтому в последнее время для предиктивного расчета рассматриваемых характеристик нашли применение аналитические и статистические подходы.

В частности, предложена статистическая методика расчета эвтектических температур и концентраций для металлических многокомпонентных систем (n > 3), исходными данными которой являются только температуры плавления компонентов, входящих в эвтектику или рассчитанные температуры плавления эвтектик при их взаимодействии. При этом в работе сформулировано температурное правило эвтектической реакции [30; 32].

Методика, предложенная в работе [32] на основе разработанного банка данных, включающая программы расчета и рекурсивного алгоритма, применима для простых систем, так как не учитывает возможность образования химических соединений в многокомпонентных системах, образования нескольких эвтектик в бинарных системах и образования твердых растворов. Этими же недостатками обладает и достаточно прогрессивная методика, учитывающая электрические заряды атомов и их взаимодействие [33]. В то же время, она значительно усложняет теоретическое обоснование и сам расчет.

Находит применение также метод расчета температур эвтектических и перитектических точек и составов двухкомпонентных систем с использованием аппроксимации зависимостей между этими характеристиками. Расчет производится с помощью дробно-линейных и степенных функций с учетом только температуры плавления компонентов [34] или путем применения линейной геометрии для расчета эвтектического состава бинарной системы при известных температурах плавления компонентов и эвтектики [35].

Одним из направлений построения схем многокомпонентных (n > 3) диаграмм состояний сплавов в традиционных координатах «температура – концентрация» является методика, предложенная в работах [36 – 38]. Она предусматривает использование «дивергентной координатной сетки Круковича» для расчета распределения элементов сплава по площади основания диаграммы – концентрационного n-угольника, количество вершин которого равно количеству химических элементов в сплаве. Сторонами многогранной призмы являются двухкомпонентные диаграммы состояний. Подобные диаграммы состояний названы «схемами диаграмм», так как на площади концентрационного многогранника отсутствует ряд сочетаний элементов сплава. В частности, нет сплавов с равным количеством трех элементов для четырехкомпонентной системы, четырех элементов для пятикомпонентной системы и т. д. Тем не менее, такие схемы весьма наглядны для использования в качестве технологического чертежа при анализе состояний сплава.

Таким образом, целью данной работы является построение поверхности ликвидус для многокомпонентной системы Fe – B – Mn – C – Cr с использованием рекомендаций [36 – 38] для определения температур насыщения и объяснения структурообразования при борировании в различном агрегатном состоянии обрабатываемых поверхностей.

Результаты исследования и их обсуждение

Процессу борирования подвергают множество марок стали и сплавов, такие, как cталь 20, 40Х, 5ХНВ, 7Х3, Х12, 10Х13, 30ХГСА, У10 и др., для повышения их износостойкости. Для большого количества конструкционных сталей характерно сочетание элементов Fe – Mn – C – Cr. Детали из этих сталей подвергают борированию как в твердом агрегатном состоянии, так и из литейных форм в жидком состоянии, а также при частичном оплавлении упрочняемых поверхностей (при наличии жидкой и твердой фаз) при использовании концентрированных источников нагрева. В этих случаях важным является знание температур плавления с участием бора, тогда система принимает вид: Fe – Cr – Mn – C – B. Последовательность элементов выбирается произвольно.

Построение поверхности ликвидус схемы пятикомпонентной диаграммы системы Fe – B – Mn – C – Cr с выбранной последовательностью элементов проводилось путем анализа структурообразования двойных диаграмм состояний сплавов. При этом использовались экспериментальные критические точки ряда сплавов системы, а также рассчитанные температуры и концентрации эвтектических взаимодействий. В частности, при определении условий борирования легированных сталей и сплавов анализу подвергались как двойные и тройные диаграммы состояния, содержащие железо, так и двойные диаграммы, содержащие только легирующие элементы и бор. При этом для прогнозирования вида боридов и степени их легированности учитывались изоморфность кристаллических решеток боридов и растворимость боридов между собой. Следует предположить, что образование того или иного базового борида при насыщении сплавов бором будет зависеть от степени сродства элементов к бору и количества этого базового элемента в сплаве. Поэтому вид поверхности ликвидус в данном случае будет определяться концентрационным распределением бора.

Система Fe – Cr – В: при нагреве до 1000 °С в равновесии с γ-Fe находятся фазы α-Fe и Fe₂В; в равновесии с α-фазой находятся γ-Fe, Fe₂В, Cr₂B, и Cr₄B. Фазы Fe₂В и особенно Cr₂B образуют широкие области твердых растворов [36]. Установлено, что в интервале температур борирования 700 – 1250 °С тройных фаз в этой системе не образуется.

Система Cr  –  Мn – В: при 800 °С установлено существование неограниченного ряда твердых растворов (Cr, Мn)В₂, (Cr, Мn)₃В₄ и между боридами Cr₂B и Мn₄В [36]. Степень взаимной растворимости боридов следующая: Cr₅B₃ растворяет 0,08 массовых долей борида Мn₅B₃, а CrB – 0,20 массовых долей МnВ; МnВ растворяет 0,4 массовых долей CrB.

При иной трактовке двойной диаграммы состояния системы Мn – В показано существование неограниченного ряда твердых растворов (Cr, Мn)₂В вместо Cr₂B – Мn₄В при 1025 °С. В исследовании [39] определены составы твердых растворов моноборидов хрома и марганца: Cr_0,46Мn_0,54В и Мn_0,60Cr_0,40В. Область между твердыми растворами на основе CrB и МnВ представляет собой борид Cr_хМn_1 – хВ.

Следует учитывать также, что изоморфные бориды Fe и Mn (FeB и MnB, Fe₂B и Mn₂B) неограниченно растворимы друг в друге.

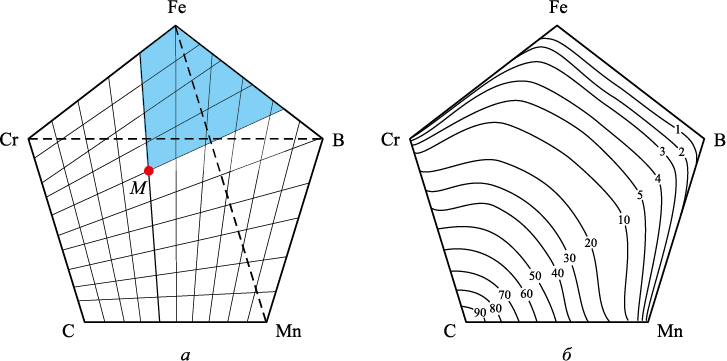
В соответствии с выбранной методикой построения схемы диаграммы каждый элемент рассматриваемой системы распределяется по объему пятигранной призмы от двух граней, а по площади основания (пятиугольника) от двух сторон. Например, углерод распределяется от сторон C – Cr и C – Mn (рис. 1). Концентрационное распределения любого элемента по площади пятиугольника, рассчитанное в соответствии с «дивергентной сеткой координат Круковича», оказывается неравномерным по его площади. Угол расхождения каждой координатной линии определялся по формуле

\[\alpha  = \left( {1 - \frac{4}{n}} \right)\frac{{180}}{c},\]

где n – число компонентов в системе (сторон многоугольника); c – количество делений равномерной концентрационной шкалы.

В рассматриваемом случае угол расхождения каждой координатной линии от предыдущей составил 3,6° при с = 10. Затемненная площадь, ограниченная координатными линиями (рис. 1), показывает содержание углерода в точке М, выраженное в процентах к площади пятиугольника. Эта площадь определялась геометрическим путем. Рассчитанное таким образом содержание в множестве точек позволяет провести изоконцентрационные линии по площади пятигранника, которые в совокупности образуют трафарет распределения любого элемента.

Для определения содержания другого элемента в точке М (например, бора) трафарет поворачивают до совмещения 100 % с вершиной В (бора). Пересечение точки М с соответствующей изоконцентрационной линией и показывает его содержание (рис. 2). В соответствии с изоконцентрационной линией оно составляет 10 мас. %.

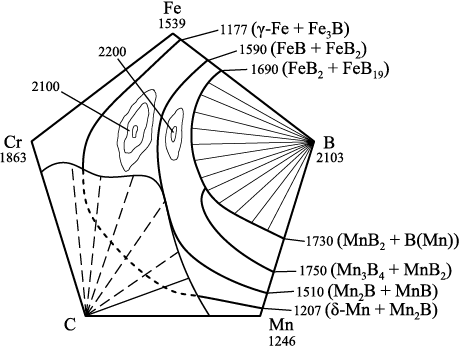
Поверхность ликвидус при выбранном расположении элементов образуется совокупностью критических точек: начала кристаллизации химических элементов и твердых растворов, температурами конгруэнтно плавящихся фаз, температурами плавления двойных эвтектик диаграмм состояния сплавов и их взаимодействия с образованием новых многокомпонентных эвтектик. Наблюдаемые два пика соответствуют образованию при этих концентрациях бора и хрома легированных боридов хрома (Cr, Fe, Mn)B (~2100 °С) и (Cr, Fe, Mn)B₂ (~2200 °С) (рис. 3).

При высоких концентрациях бора происходит взаимодействие высокотемпературных эвтектик двойных диаграмм состояний Fe – B и Mn – B с образованием новой эвтектической смеси FeB₂ + FeB₁₉ + Mn₃B₄ + MnB₂ + B(Mn) с рассчитанной температурой плавления 1571 °С. В присутствии достаточного количества хрома и концентрации бора в интервале 27,92 – 90,0 мас. % возможно образование эвтектики, содержащей (Fe, Mn)B₂ + FeB₁₉ + Mn₃B₄ + B(CrMn) + CrB₂ с рассчитанной температурой плавления 1394 °С.

В области концентраций бора, равных 16,25 – 27,92 мас. %, происходит взаимодействие эвтектик FeB + FeB₂ и Mn₂B + С с образованием эвтектической смеси (Fe, Mn)B + FeB₂ + Mn₂B с рассчитанной температурой плавления 1451 °С.

При концентрациях бора 0,01 – 10 мас. % в результате взаимодействия эвтектик γ-Fe – Fe₃B и δ-Mn + Mn₂B образуется новая эвтектическая смесь, содержащая γ-Fe + Fe₃B + δ-Mn + Mn₂B с рассчитанной температурой плавления 1105 °С, а при содержании хрома >40 мас. % возможно образование эвтектики (γ-Fe + Fe₃B + δ-Mn + Mn₂B) + Cr(B) + Cr₂B с температурой плавления 978 °С. Приведенные фазовые составы от взаимодействия эвтектик даны без учета растворимости боридов друг в друге.

Температуры существования конгруэнтно плавящихся боридов FeB, FeB₂, Mn₂B, Mn₃B₄, MnB, Mn₃B₄, MnB₂ и их взаимодействие не нанесены на поверхность ликвидус для лучшего восприятия. Температура поверхности ликвидус имеет важное значение при борировании отливок из литейных форм, на внутренние поверхности которых нанесена борирующая обмазка, и при предопределении фазового состава слоя.

Рассчитанные температуры плавления новых эвтектик образуют минимальные температуры начала плавления сплавов, т. е. температуры поверхности солидус. Она является границей формирования борированных слоев по диффузионному механизму в твердом агрегатном состоянии обрабатываемых поверхностей деталей и по диффузионно-кристаллизационному механизму в затвердевающем состоянии поверхностей.

Эвтектические температуры рассчитывались в соответствии с правилом эвтектических реакций Круковича [17; 30; 31; 36 – 38; 40] по формулам:

– для четного числа компонентов (2n) эвтектики

\[{T_{{\rm{эвт}}}} = K_{{\rm{эвт}}}^{n/2}\sum\limits_{i = 1}^n {{T_i}} ;\]

– для нечетного числа компонентов (2n + 1)

\[\begin{array}{c}{T_{{\rm{эвт}}}} = K_{{\rm{эвт}}}^{\frac{{n + 1}}{2}}\sum\limits_{i = 1}^{n - 1} {{T_i} + {K_{{\rm{эвт}}}}{T_n}} ;\\{K_{{\rm{эвт}}}} = 0,497\exp ( - 0,2657X);\\X = \frac{{\sum\limits_{1 \le i \le j \le n}^n {\left| {{T_i} - {T_j}} \right|} }}{{{{\left( {\sum\limits_{i = 1}^n {{T_i}} } \right)}^{0,74}}}},\end{array}\]

где Т – температуры плавления фаз, входящих в эвтектику, или температуры двойных (тройных) эвтектических взаимодействий как элементов новой эвтектики, К; K_эвт – коэффициент эвтектической температуры; X – масштабный температурный параметр.

В соответствии с правилом эвтектических реакций при расчете эвтектической температуры новой эвтектики применялись температуры плавления бинарных эвтектик или уже рассчитанных, компоненты которых и являлись компонентами новых эвтектических смесей.

Фазовый состав, структурная морфология и свойства получаемых борированных слоев определяются содержанием легирующих элементов в стали, температурой насыщения и насыщающей способностью среды. В частности, при борировании стали 40Х, содержащей 0,36 – 0,44 % С, 0,17 – 0,27 % Si, 0,5 – 0,8 % Mn и 0,8 – 1,1 % Cr, при температуре насыщения 950 °С в борирующей смеси, обеспечивающей концентрацию бора ~17 %, образуются слои на основе легированных боридов (Fe, Cr)B + (Fe, Cr, Mn)₂B. При превышении температуры плавления формируются слои с гетерогенной структурой, в которой дисперсные легированные бориды располагаются в α-твердом растворе.

Выводы

Дивергентная концентрационная сетка позволила определить распределение каждого элемента по объему пятигранной призмы путем построения концентрационного трафарета.

Применяя правило эвтектических реакций, рассчитаны эвтектические температуры и определен фазовый состав взаимодействующих эвтектик в системе Fe – B – Mn – C – Cr.

Определение закономерностей структурообразования при борировании в жидком, кристаллизующемся или твердом состояниях обрабатываемых поверхностей рекомендуется проводить с использованием построенной поверхности ликвидус для схемы пятикомпонентной диаграммы состояний системы Fe – B – Mn – C – Cr и рассчитанных температур плавления эвтектик, образующих поверхность солидус системы.