Construction of liquidus surface of Fe – B – Mn – C – Cr five-component diagram

Introduction

Phase diagrams of alloys serve as essential reference tools for both theorists and practitioners in metallurgy, materials science, metal forming, casting, various fields of mechanical engineering, and the operation of technical equipment.

Taking into account that most of the steels and alloys used are multicomponent (n > 3), in many cases certain difficulties arise in determining the conditions for performing technological processes, the phase composition and properties of alloys, since there are no constructed state diagrams in the temperature-concentration traditional coordinates [1 – 3]. Typically, binary and ternary diagrams, their isothermal sections, tetrahedral representations for specific temperatures, and practical research findings are used to describe these processes [4 – 6].

In particular, binary and ternary phase diagrams have been widely applied to describe the boriding process and the properties of boronized layers [7 – 9]. These diagrams refine the concentrations of compounds and solid solutions, define phase transformation temperatures, and reveal new compounds. A key finding is the confirmed existence of iron borocarbide [8; 9], which has the formula Fe₂₃(C, B)₆. In other complex carbides found in steels, alloying elements typically substitute for iron.

It has been established that at 1000 °C, up to 80 % of the carbon in cementite can be replaced by boron, modifying the formula to Fe₃C_0.2B_0.8. This substitution alters the crystal lattice parameters, leading to compression along the a and c axes and expansion along the b axis of the orthorhombic lattice. Additionally, as boron content increases, the saturation magnetization and Curie temperature also rise. This phenomenon is crucial in explaining the properties of borided components, where borocarbide inclusions form beneath the boride layer [10; 11].

Study [8] demonstrated that borocarbide Fe₂₃(C, B)₆ is isomorphic to cubic chromium carbide Cr₂₃C₆ (structure type d84). As the composition shifts from carbon-enriched to boron-enriched, the lattice parameter a increases from 1.0594 to 1.0628 nm. When heated to 800 °C Fe₂₃(C, B)₆ melts congruently. Isothermal sections at 700, 800, 900, and 1000 °C indicate that the Fe₂₃(C, B)₆ phase has a composition corresponding to Fe₂₃(C_0.73B_0.27)₆ and is in equilibrium with borocementite Fe₃(C, B) and Fe_α. The phase Fe₂₃(C_0.44B_0.56)6 is in equilibrium with Fe₂B and Fe₃(C, B). An analysis of the section at 800 °C shows that Fe₂₃(C, B)₆ exists over a wider range of carbon and boron concentrations, between Fe₂₃(C_0.38B_0.62)₆ and Fe₂₃(C_0.77B_0.23)₆, and is in equilibrium with Fe_γ and Fe₃(C, B). It has been determined that Fe₂₃(C, B)₆ remains stable up to 965 ± 5 °C [12 – 14]. These findings refine the phase composition of phase diagram regions and the properties of borided layers, as borocarbide inclusions exhibit high hardness [15 – 17].

In the study of multicomponent phase diagrams (n > 3), the thermodynamic method, which incorporates the characteristics of binary phase diagrams, has been widely used [18]. Specifically, a four-component Fe – Mn – Si – C phase diagram was developed by calculating thermodynamic constants at the phase transformation temperatures of compounds, followed by triangulation of the system and its subsystems. This resulted in a tetrahedral phase diagram consisting of 16 elementary tetrahedra containing congruently and incongruently melting compounds [19].

The Bukke-Schout method [20] represents the system’s composition or state as a tetrad on a plane, though it is derived from a four-dimensional figure. However, the systems described in studies [21; 22] create geometric representations of multicomponent compositions in two dimensions, making them less suitable for practical applications. The refinements of the general approach discussed in studies [23; 24] do not produce practical working diagrams but instead generate planar projection systems after double projection, which are also difficult to use as working schematics in technological process development.

To determine the temperatures of eutectic reactions and the compositions of eutectic alloys, differential scanning calorimetry [25; 26], metallographic studies [27; 28], and X-ray diffraction analysis [29] have traditionally been used. These methods, however, are labor-intensive, leading to the increasing use of analytical and statistical approaches for predictive calculations of these characteristics.

A statistical method has been proposed for calculating eutectic temperatures and concentrations in metallic multicomponent systems (n > 3), where the only input data are the melting temperatures of the components forming the eutectic or the calculated eutectic melting temperatures resulting from their interaction. In this context, a temperature rule for eutectic reactions has been formulated [30; 32].

The methodology proposed in study [32], based on a developed database incorporating calculation programs and a recursive algorithm, is applicable to simple systems. However, it does not account for the formation of chemical compounds in multicomponent systems, the presence of multiple eutectics in binary systems, or the formation of solid solutions. A more advanced method that considers atomic electric charges and their interactions [33] also has these limitations, while further complicating theoretical justification and calculations.

Another approach involves calculating eutectic and peritectic temperatures and compositions in binary systems using approximation techniques to model the relationships between these characteristics. These calculations are performed using fractional-linear and power functions, relying only on the melting temperatures of the components [34], or by applying linear geometry to determine the eutectic composition of a binary system based on the known melting temperatures of its components and eutectic [35].

One method for constructing schemes of multicomponent (n > 3) phase diagrams in traditional temperature – concentration coordinates is the approach proposed in studies [36 – 38]. This method uses the Krukovich divergent coordinate grid to determine the distribution of alloying elements over the diagram’s base area – a concentration n-gon, where the number of vertices corresponds to the number of chemical elements in the alloy. The sides of the polyhedral prism represent binary phase diagrams. These phase diagrams, referred to as diagram schemes, omit certain combinations of alloying elements in the concentration polyhedron. Specifically, alloys with equal proportions of three elements are absent in a four-component system, four elements in a five-component system, and so on. Nevertheless, these schemes provide a highly illustrative representation and can serve as a technological reference diagram for analyzing alloy states.

Thus, this study aims to construct the liquidus surface for the multicomponent Fe – B – Mn – C – Cr system, following the recommendations from [36 – 38] to determine saturation temperatures and explain the structural formation processes that occur during boriding in different aggregate states of treated surfaces.

Results and discussion

A wide range of steel grades and alloys, including (AISI) C1020, 5140, L6, D3, 430, SCSiMn2 (Japanese), W 1-0.8 C EXTRA, and others, undergo boriding to enhance wear resistance. Many structural steels are characterized by a combination of Fe – Mn – C – Cr elements. Components made from these steels are borided in both the solid state and the liquid state within casting molds, as well as through partial remelting of the hardened surfaces (in the presence of both liquid and solid phases) when using concentrated heat sources. In such cases, knowledge of melting temperatures involving boron is essential, leading to a system represented as Fe – Cr – Mn – C – B, where the sequence of elements is chosen arbitrarily.

The construction of the liquidus surface for the five-component Fe – B – Mn – C – Cr phase diagram, with the selected sequence of elements, was carried out by analyzing the structural formation of binary phase diagrams of alloys. This process incorporated experimental critical points of several alloys in the system, as well as calculated temperatures and concentrations of eutectic interactions. In particular, when determining boriding conditions for alloy steels and alloys, both binary and ternary phase diagrams containing iron were analyzed, along with binary diagrams that included only alloying elements and boron. To predict the type of borides and their degree of alloying, the isomorphism of boride crystal lattices and the solubility of borides within each other were considered. It can be assumed that the formation of a particular primary boride during alloy saturation with boron depends on the affinity of the elements for boron and the amount of the base element in the alloy. Therefore, in this case, the shape of the liquidus surface is determined by the concentration distribution of boron.

Fe – Cr – В system: at 1000 °C, the phases in equilibrium with γ-Fe include α-Fe and Fe₂B, while those in equilibrium with the α-phase include γ-Fe, Fe₂B, Cr₂B, and Cr₄B. The Fe₂B and, particularly, Cr₂B phases form extensive regions of solid solutions [36]. It has been established that within the boriding temperature range of 700 – 1250 °C, no ternary phases are formed in this system.

Cr  –  Мn – В system: at 800 °C, an unlimited series of solid solutions (Cr, Mn)B₂, (Cr, Mn)₃B₄, and between Cr₂B and Mn₄B borides has been identified [36]. The degree of mutual solubility of borides is as follows: Cr₅B₃ dissolves 0.08 mass fractions of Mn₅B₃ boride, while CrB dissolves 0.20 mass fractions of MnB; MnB dissolves 0.4 mass fractions of CrB.

An alternative interpretation of the binary phase diagram for the Mn – B system suggests the existence of an unlimited series of solid solutions (Cr, Мn)₂В instead of the Cr₂B – Мn₄В system at 1025 °C. Study [39] determined the compositions of solid solutions of chromium and manganese monoborides: Cr_0.46Мn_0.54В and Мn_0.60Cr_0.40В. The region between the solid solutions based on CrB and MnB corresponds to the Cr_хМn_1 – хВ boride.

It should also be noted that isomorphic borides of Fe and Mn (FeB and MnB, Fe₂B and Mn₂B) exhibit unlimited mutual solubility.

According to the selected technique for constructing schemes of multicomponent phase diagrams, each element of the system is distributed within the volume of the pentahedral prism from two faces and across the base area (a pentagon) from two sides. For example, carbon is distributed from the C – Cr and C – Mn sides (Fig. 1). The concentration distribution of any element across the pentagon’s surface, calculated using the divergent coordinate grid, is non-uniform. The divergence angle of each coordinate line was determined by the formula

\[\alpha  = \left( {1 - \frac{4}{n}} \right)\frac{{180}}{c},\]

where n is the number of components in the system (i.e., the number of polygon sides), and c is the number of divisions on the uniform concentration scale.

In this case, the divergence angle of each coordinate line from the previous one is 3.6° for c = 10. The shaded area enclosed by the coordinate lines (Fig. 1) represents the carbon content at point M, expressed as a percentage of the pentagon’s total area. This area was determined geometrically. The calculated concentrations at multiple points allowed for the construction of iso-concentration lines across the base of the pentahedral prism, collectively forming a stencil for element distribution.

To determine the concentration of another element at point M (e.g., boron), the stencil is rotated so that 100 % aligns with vertex B (boron). The intersection of point M with the corresponding iso-concentration line indicates the boron content (Fig. 2), which, in this case, is 10 wt. %.

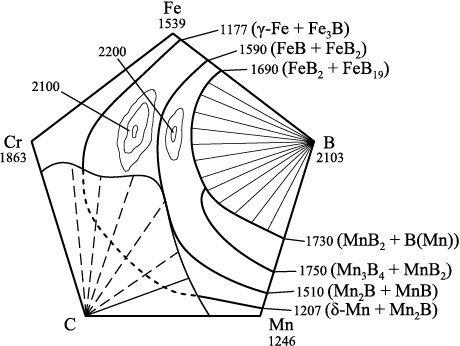
The liquidus surface for the selected element arrangement is formed by a set of critical points, including the onset of crystallization of chemical elements and solid solutions, the melting temperatures of congruently melting phases, the melting points of binary eutectics from phase diagrams of alloys, and their interactions leading to the formation of new multicomponent eutectics. The two observed peaks correspond to the formation of alloyed chromium borides (Cr, Fe, Mn)B (~2100 °C) and (Cr, Fe, Mn)B₂ (~2200 °C) at these boron and chromium concentrations (Fig. 3).

At high boron concentrations, high-temperature eutectics from the Fe – B and Mn – B binary phase diagrams interact, forming a new eutectic mixture FeB₂ + FeB₁₉ + Mn₃B₄ + MnB₂ + B(Mn) with a calculated melting temperature of 1571 °C. In the presence of a sufficient amount of chromium and a boron concentration in the range of 27.92 – 90.0 wt. %, the formation of a eutectic containing (Fe, Mn)B₂ + FeB₁₉ + Mn₃B₄ + B(CrMn) + CrB₂ possible, with a calculated melting temperature of 1394 °С.

At boron concentrations between 16.25 and 27.92 wt. %, the interaction of FeB + FeB₂ and Mn₂B + С eutectics results in the formation of a eutectic mixture (Fe, Mn)B + FeB₂ + Mn₂B с with a calculated melting temperature of 1451 °С.

At boron concentrations between 0.01 and 10 wt. %, the interaction of the γ-Fe – Fe₃B and δ-Mn + Mn₂B eutectics leads to the formation of a new eutectic mixture γ-Fe + Fe₃B + δ-Mn + Mn₂B a calculated melting temperature of 1105 °С. At chromium concentrations above 40 wt. %, another eutectic may form (γ-Fe + Fe₃B + δ-Mn + Mn₂B) + Cr(B) + Cr₂B with a melting temperature of 978 °C. The phase compositions resulting from eutectic interactions are presented without considering the mutual solubility of borides.

The melting temperatures of congruently melting borides FeB, FeB₂, Mn₂B, Mn₃B₄, MnB, Mn₃B₄, MnB₂ and their interactions are not included in the liquidus surface visualization for clarity. The temperature of the liquidus surface is crucial for boriding castings in molds coated with a boriding mixture, as well as for predicting the phase composition of the boronized layer.

The calculated melting temperatures of new eutectics represent the lowest temperatures at which alloy melting begins, i.e., the solidus surface temperature. This temperature defines the boundary for the formation of boronized layers through a diffusion mechanism in the solid state of treated surfaces and a diffusion-crystallization mechanism in the solidifying state of surfaces.

Eutectic temperatures were calculated in accordance with Krukovich’s eutectic reaction rule [17; 30; 31; 36 – 38; 40] using the following formulas:

– for an even number of eutectic components (2n)

\[{T_{{\rm{eut}}}} = K_{{\rm{eut}}}^{n/2}\sum\limits_{i = 1}^n {{T_i}} ;\]

– for an odd number of eutectic components (2n + 1)

\[\begin{array}{c}{T_{{\rm{eut}}}} = K_{{\rm{eut}}}^{\frac{{n + 1}}{2}}\sum\limits_{i = 1}^{n - 1} {{T_i} + {K_{{\rm{eut}}}}{T_n}} ;\\{K_{{\rm{eut}}}} = 0.497\exp ( - 0.2657X);\\X = \frac{{\sum\limits_{1 \le i \le j \le n}^n {\left| {{T_i} - {T_j}} \right|} }}{{{{\left( {\sum\limits_{i = 1}^n {{T_i}} } \right)}^{0.74}}}},\end{array}\]

where Т represents the melting temperatures of eutectic phases or the melting temperatures of binary (or ternary) eutectic interactions, which form the components of a new eutectic mixture, K; K_eut is the eutectic temperature coefficient, and X is a temperature scaling parameter.

According to the eutectic reaction rule, when calculating the eutectic temperature of a new eutectic, the melting temperatures of binary eutectics or previously calculated eutectics (whose components also form part of the new eutectic mixture) were used.

The phase composition, structural morphology, and properties of boronized layers depend depend on the content of alloying elements in the steel, the saturation temperature, and the saturation potential of the environment. Specifically, during the boriding of 5140 steel (AISI), which contains contains 0.36 – 0.44 % C, 0.17 – 0.27 % Si, 0.5 – 0.8 % Mn, and 0.8 – 1.1 % Cr, at a saturation temperature of 950 °C in a boriding mixture ensuring a boron concentration of ~17 %, layers based on alloyed borides (Fe, Cr)B + (Fe, Cr, Mn)₂B are formed. When the melting temperature is exceeded, heterogeneous layers develop, where dispersed alloyed borides are embedded in an α-solid solution.

Conclusions

The divergent coordinate grid was used to determine the element distribution within the volume of the pentahedral prism by constructing a concentration stencil.

Using the eutectic reaction rule, eutectic temperatures were calculated, and the phase composition of interacting eutectics in the Fe – B – Mn – C – Cr system was determined.

To analyze the structural formation mechanisms during boriding in the liquid, crystallizing, or solid states of treated surfaces, it is recommended to use the constructed liquidus surface of the five-component phase diagram scheme for the Fe – B – Mn – C – Cr system, along with the calculated eutectic melting temperatures, which define the solidus surface of the system.