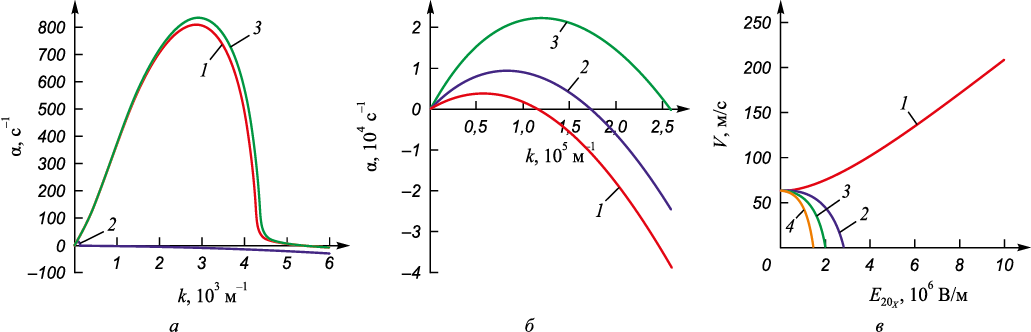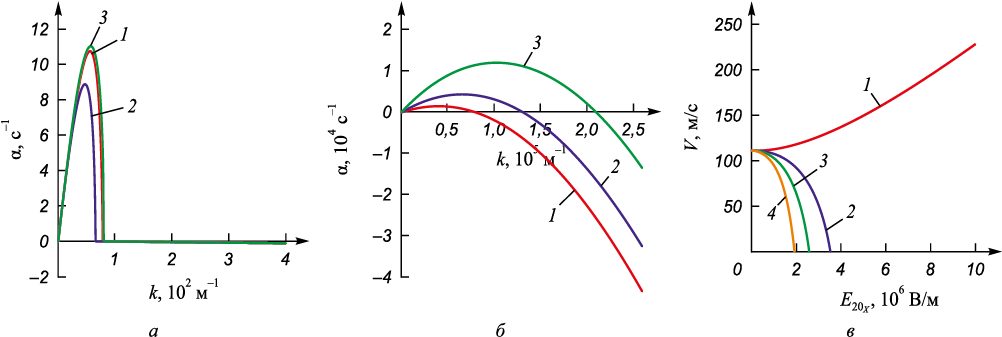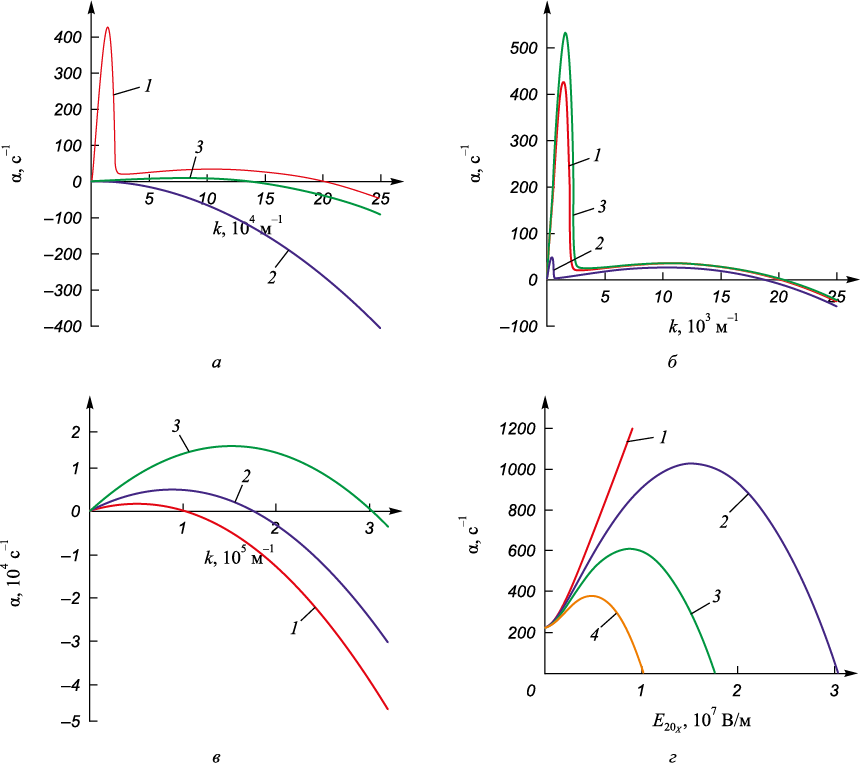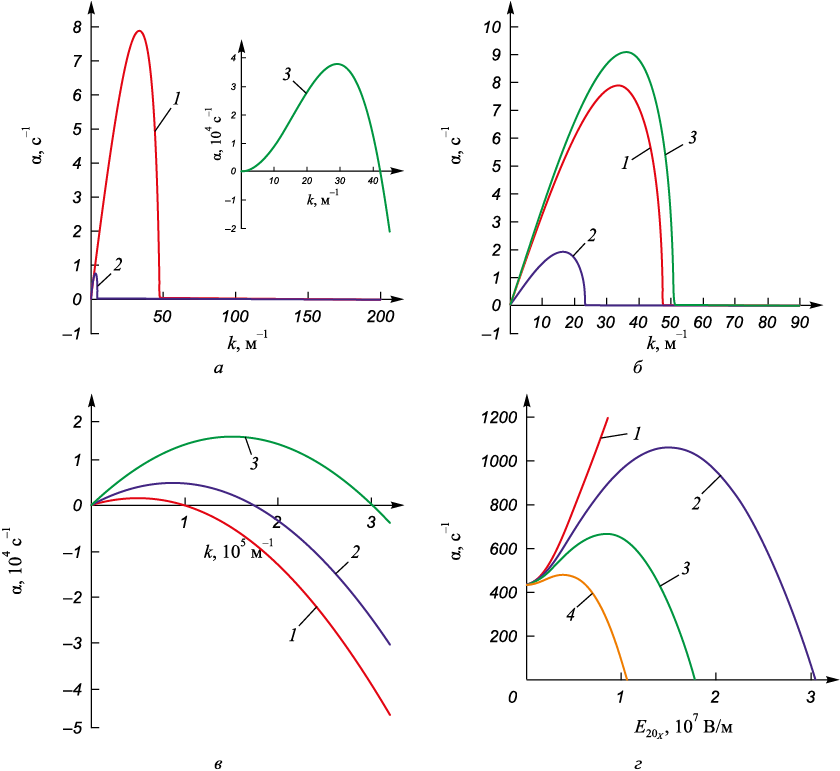Перейти к:
Влияние наклонного электрического поля на распад струи жидкости в процессах термообработки и наплавки
https://doi.org/10.17073/0368-0797-2025-1-30-39
Аннотация
Изучено совместное воздействие наклонных электрических полей и поперечного акустического поля на неустойчивость Кельвина–Гельмгольца границы раздела вязких электропроводных жидкостей на примере систем воздух – вода и аргон – железо. Наклонное электрическое поле вне зависимости от воздействия звуковых колебаний приводит к усилению неустойчивости Кельвина–Гельмгольца в микрометровом диапазоне длин волн. Наиболее интенсивный рост возмущений поверхности раздела наблюдается при угле наклона электрического поля π/3. Это открывает новые возможности для разработки технологий ускоренного охлаждения проката и наплавки материалов путем регулирования капельного переноса материала. Совместное воздействие акустических и электрических полей оказывает неоднозначное влияние на неустойчивость Кельвина–Гельмгольца. В случае системы воздух – вода звуковые колебания приводят к подавлению неустойчивости Кельвина–Гельмгольца, при этом тангенциальное электрическое поле напряженностью 3·106 В/м усиливает данный эффект, а нормальное поле, наоборот, ослабляет его. Для системы аргон – железо звуковые колебания приводят к полному исчезновению вязкостно-обусловленного максимума и к значительному снижению скорости роста возмущений поверхности раздела, которая соответствует первому максимуму. Приложение горизонтального электрического поля напряженностью 3·107 В/м значительно ослабляет эффект подавления неустойчивости Кельвина–Гельмгольца, а в вертикальном поле он, наоборот, усиливается. Установлено, что восстановление первого гидродинамического максимума в нормальном электрическом поле возможно при соотношении удельных электрических проводимостей σ более 0,012 вне зависимости от наличия звукового поля. Смена знака влияния вертикального электрического поля со стабилизирующего на дестабилизирующее возможно при соотношении σ от 0,015 и более.
Ключевые слова
Для цитирования:
Невский С.А., Бащенко Л.П., Сарычев В.Д., Грановский А.Ю., Шамсутдинова Д.В. Влияние наклонного электрического поля на распад струи жидкости в процессах термообработки и наплавки. Известия высших учебных заведений. Черная Металлургия. 2025;68(1):30-39. https://doi.org/10.17073/0368-0797-2025-1-30-39
For citation:
Nevskii S.A., Bashchenko L.P., Sarychev V.D., Granovskii A.Yu., Shamsutdinova D.V. Influence of inclined electric field on decay of a liquid jet during heat treatment and surfacing. Izvestiya. Ferrous Metallurgy. 2025;68(1):30-39. https://doi.org/10.17073/0368-0797-2025-1-30-39
Введение
Неустойчивость Кельвина–Гельмгольца встречается во многих областях исследований, начиная с земной магнитной гидродинамики [1], турбулентного перемешивания жидкостей [2], процессов нанесения покрытий электрическим взрывом [3] и заканчивая такими астрофизическими эффектами, как солнечный ветер [4]. Данная неустойчивость является мощным триггером, который препятствует устойчивости систем, где происходит смешивание двух или более жидкостей с различными свойствами. Наиболее интересными приложениями неустойчивости являются акустические режимы в системах, потребляющих воздух, таких как котлы, авиационные реактивные двигатели, газовые турбины [5]. Не менее интересным приложением данной неустойчивости является распад струи на капли в электрическом поле [6; 7]. Это явление лежит в основе принципа действия прецизионных устройств, являющихся неотъемлемой частью различных технологических процессов, например, электродуговой сварки, получения ультрамелкодисперсных порошков тугоплавких материалов [6; 7]. В работе [8] при изучении воздействия наклонного электрического поля на неустойчивость Кельвина–Гельмгольца двух идеальных диэлектрических жидкостей были найдены условия перехода жидкости в устойчивый режим при наложении горизонтального электрического поля, а также показано, что вертикальная компонента электрического поля оказывает дестабилизирующее влияние. Другим весьма перспективным приложением такой неустойчивости является ускоренное охлаждение арматурного проката. В работе [9] показано, что, регулируя скорость движения в системе вода – пар, можно добиться формирования капель наноразмерного диапазона. Эти капли, попадая на прокат, возбуждают термоупругую волну и тем самым увеличивают его ударную вязкость.
Возникновение и развитие неустойчивости Кельвина–Гельмгольца двух вязких жидкостей изучалось в работах [10; 11]. Особенность этих работ заключается в том, что в них используется вязко-потенциальное приближение. Его суть заключается в том, что сдвиговые компоненты тензора напряжений на границе раздела сред отсутствуют, а вязкость жидкости учитывается только в условии непрерывности нормальных напряжений на данной границе [10]. В общем случае ситуация осложняется тем, что необходимо знать профиль скоростей среды и, как показывают результаты работ [11; 12], аналитического решения задачи устойчивости течения для профиля сложной конфигурации не существует. Однако при больших волновых числах (коротких длинах волн) данное приближение, как показывают результаты работы [13], является оправданным.
Взаимодействие неустойчивости Кельвина–Гельмгольца с ультразвуковыми колебаниями для случая плоской геометрии задачи в приближении вязко-потенциального течения изучалось в работах [14; 15]. Предполагалось, что воздействие акустических колебаний эквивалентно эффективному колеблющемуся полю сил тяжести. Установлено, что акустическое воздействие приводит к смещению максимума скорости роста в область больших волновых чисел [15] и обнаружена область стабильности между режимами слабого акустического воздействия и параметрического резонанса.
Целью настоящей работы являлось изучение совместного влияния наклонного электрического поля и поперечного акустического поля на устойчивость плоской поверхности электропроводной жидкости на примере систем железо – аргон и вода – воздух в приближении вязко-потенциального течения. Одновременное применение этих двух воздействий позволит добиться создания микро- и нанокапельных режимов течения жидкости, что является важным для разработки новых технологий сварки, наплавки, а также ускоренного охлаждения проката.
Постановка задачи
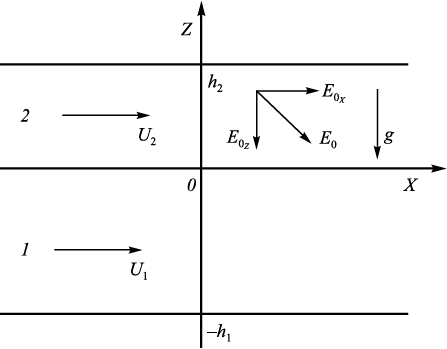
Рассмотрим неустойчивость плоской поверхности раздела двух вязких электропроводных сред. Первая среда характеризуется плотностью ρ1 , кинематической вязкостью ν1 , проводимостью σ1 и диэлектрической проницаемостью ε1 (рис. 1). Она занимает область (–∞ ≤ x ≤ +∞ и –h1 ≤ z ≤ 0) и движется с горизонтальной скоростью U1 . Вторая среда занимает область (–∞ ≤ x ≤ +∞ и 0 ≤ z ≤ h2 ) и обладает плотностью ρ2 , кинематической вязкостью ν2 , проводимостью σ2 и диэлектрической проницаемостью ε2 . Горизонтальная скорость второй среды U2 . Переменная ξ представляет собой отклонение границы раздела от равновесного значения (рис. 1).
Рис. 1. К постановке задачи о возникновении и развитии |
Скорости движения первой и второй сред много меньше скорости звука, поэтому будем их считать несжимаемыми. Кинематика движения поверхности раздела описывается функцией F(x, z, t) = z – ξ(x, t). Тогда вектор нормали определяется как \(\vec n = \frac{{\nabla F}}{{\left| {\nabla F} \right|}} = \frac{{ - \frac{{\partial \xi }}{{\partial x}}{{\vec e}_x} + {{\vec e}_z}}}{{\sqrt {1 + {{\left( {\frac{{\partial \xi }}{{\partial x}}} \right)}^2}} }}\) (где \(\nabla \) ‒ оператор градиента). В линейном приближении вектор нормали примет вид \(\vec n = - \frac{{\partial \xi }}{{\partial x}}{\vec e_x} + {\vec e_z}\). Рассматриваемая система помещена во внешние поперечное акустическое поле и наклонное электрическое поле по отношению к поверхности жидкости (рис. 1). Вектор электрического поля с учетом возмущений поверхности раздела примет вид \(\vec E = {E_{0x}}{\vec e_x} - {E_{0z}}{\vec e_z} - \nabla \psi \) (где ψ – возмущение электрического потенциала; E0x и E0z – нормальная и тангенциальная составляющие невозмущенного электрического поля соответственно). Значение угла наклона вектора электрического поля (рис. 1) по отношению к невозмущенной поверхности β определим как \({\rm{arctg}}\left( {\frac{{{E_{0z}}}}{{{E_{0x}}}}} \right)\).
Основные линеаризованные уравнения модели вязко-потенциального течения относительно малых возмущений с учетом электрического поля, согласно [10; 15], будут иметь вид:
| \[\begin{array}{c}\Delta {\Phi _1} = 0;{\rm{ }} - {h_1} < z < 0;{\rm{ }}\\\Delta {\Phi _2} = 0;{\rm{ }}0 < r < {h_2};\\\Delta {\psi _1} = 0;{\rm{ }} - {h_1} < z < 0;{\rm{ }}\\\Delta {\psi _2} = 0;{\rm{ }}0 < r < {h_2},\end{array}\] | (1) |
где Φ ‒ возмущение потенциала скорости.
При получении первого и второго уравнений системы (1) не учитывали члены, связанные с электрическим полем, что справедливо для электропроводных жидкостей [16 ‒ 18], когда отсутствует объемный заряд. Поэтому будем учитывать электрическую составляющую только в условиях на границе раздела жидкости и газа. На границах h2 и h1 зададим условия отсутствия возмущений скорости течения и электрического поля:
| \[\begin{array}{l}z = - {h_1}:{\rm{ }}\;\frac{{\partial {\Phi _1}}}{{\partial z}} = 0;{\rm{ }}\;\frac{{\partial {\psi _1}}}{{\partial x}} = 0;{\rm{ }}\\{\rm{ }}z = {h_2}:{\rm{ }}\;\frac{{\partial {\Phi _2}}}{{\partial z}} = 0;{\rm{ }}\;\frac{{\partial {\psi _2}}}{{\partial x}} = 0.\end{array}\] | (2) |
Граничные условия для возмущений потенциалов течения жидкости на поверхности раздела сред c учетом электрического поля имеют вид:
| \[\begin{array}{c}z = 0:{\rm{ }}\;\frac{{\partial {\Phi _1}}}{{\partial z}} = \frac{{\partial \xi }}{{\partial t}} + {U_1}\frac{{\partial \xi }}{{\partial z}};{\rm{ }}\;\frac{{\partial {\Phi _2}}}{{\partial z}} = \frac{{\partial \xi }}{{\partial t}} + {U_2}\frac{{\partial \xi }}{{\partial z}};{\rm{ }}\\ - {p_1} + 2{\rho _1}{\nu _1}\frac{{{\partial ^2}{\Phi _1}}}{{\partial {z^2}}} + {p_{s1}} - \frac{1}{2}{\varepsilon _1}{\varepsilon _0}\left( {E_{1n}^2 - E_{1\tau }^2} \right) + \\ + {p_2} - 2{\rho _2}{\nu _2}\frac{{{\partial ^2}{\Phi _2}}}{{\partial {z^2}}} - {p_{s2}} + \frac{1}{2}{\varepsilon _2}{\varepsilon _0}\left( {E_{2n}^2 - E_{2\tau }^2} \right) = \gamma \frac{{{\partial ^2}\xi }}{{\partial {x^2}}},\end{array}\] | (3) |
где Ui – скорость движения i-й среды; \({p_i} = - {\rho _i}\left( {\frac{{\partial {\Phi _i}}}{{\partial t}} + {U_i}\frac{{\partial {\Phi _i}}}{{\partial x}}} \right)\) ‒ возмущение давления в i-й среде; psi ‒ возмущение давления акустического поля; i = 1, 2 ‒ номер среды; γ – поверхностное натяжение; Ein и Eiτ ‒ нормальная и тангенциальная составляющая поля соответственно.
Условия для электрического поля на границе раздела сред определим как [19]:
| \[\vec n \cdot {\vec E_1} = \vec n \cdot {\vec E_2};{\rm{ }}{\sigma _1}\left( {\vec n \cdot {{\vec E}_1}} \right) = {\sigma _2}\left( {\vec n \cdot {{\vec E}_2}} \right).\] | (4) |
Подстановка в зависимость (4) вышеприведенных значений вектора нормали и электрического поля и последующая линеаризация с учетом того, что на границе раздела двух проводников σ1E01z = σ2E02z , E01x = E02x , приводят к следующему:
| \[\begin{array}{c}{E_{10z}}\frac{{\partial \xi }}{{\partial x}} + \frac{{\partial {\psi _1}}}{{\partial x}} = {E_{20z}}\frac{{\partial \xi }}{{\partial x}} + \frac{{\partial {\psi _2}}}{{\partial x}};{\rm{ }}\\{\sigma _1}\left( {{E_{10x}}\frac{{\partial \xi }}{{\partial x}} + \frac{{\partial {\psi _1}}}{{\partial z}}} \right) = {\sigma _2}\left( {{E_{20x}}\frac{{\partial \xi }}{{\partial x}} + \frac{{\partial {\psi _2}}}{{\partial z}}} \right).\end{array}\] | (5) |
Решение уравнений (1) будем искать в виде:
| \[\begin{array}{c}{\Phi _1}(x,z,t) = {A_1}\cosh \left[ {k(z + {h_1})} \right]\exp (\omega t + ikx);\\{\Phi _2}(x,z,t) = {A_2}\cosh \left[ {k(z - {h_2})} \right]\exp (\omega t + ikx);\\{\psi _1}(x,z,t) = {A_3}\sinh \left[ {k(z + {h_1})} \right]\exp (\omega t + ikx);\\{\psi _2}(x,z,t) = {A_4}\sinh \left[ {k(z - {h_2})} \right]\exp (\omega t + ikx);\\\xi (x,t) = {\xi _0}\exp (\omega t + ikx).\end{array}\] | (6) |
Подстановка третьего, четвертого и пятого уравнения (6) в зависимость (5) приводит к следующей системе уравнений для постоянных A3 и A4 :
| \[\begin{array}{c}{A_3}\sinh (k{h_1}) + {A_4}\sinh (k{h_2}) = \left( {{E_{20z}} - {E_{10z}}} \right){\xi _0};\\{A_3}{\sigma _1}\cosh (k{h_1}) - {A_4}{\sigma _2}\cosh (k{h_2}) = \\ = i{\xi _0}\left( {{\sigma _2}{E_{20x}} - {\sigma _1}{E_{10x}}} \right).\end{array}\] | (7) |
Решение (7) после преобразования имеет вид:
| \[\begin{array}{c}{A_3} = - \left\{ {\left[ {i\left( {{\sigma _1}{E_{10x}} - {\sigma _2}{E_{20x}}} \right) + \left( {{\sigma _2}{E_{10z}} - {\sigma _2}{E_{20z}}} \right)} \right. \times } \right.\\ \times \left. {\left. {\coth (k{h_2})} \right]{\xi _0}} \right\} \times \\ \times {\left\{ {\sinh (k{h_1})\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\}^{ - 1}};\\{A_4} = - \left\{ {\left[ {i\left( {{\sigma _1}{E_{10x}} - {\sigma _2}{E_{20x}}} \right) + \left( {{\sigma _1}{E_{20z}} - {\sigma _1}{E_{10z}}} \right)} \right. \times } \right.\\ \times \left. {\left. {\coth (k{h_1})} \right]{\xi _0}} \right\} \times \\ \times {\left\{ {\sinh (k{h_2})\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\}^{ - 1}}.\end{array}\] | (8) |
Тогда возмущения электрического потенциала будут иметь следующий вид:
| \[\begin{array}{c}{\psi _1}(x,z,t) = - \left\{ {\left[ {i({\sigma _1}{E_{10x}} - {\sigma _2}{E_{20x}}) + } \right.} \right.\\ + \left. {({\sigma _2}{E_{10z}} - {\sigma _2}{E_{20z}})\coth (k{h_2})} \right]\sinh \left[ {k(z + {h_1})} \right]/\\/\left\{ {\sinh (k{h_1})\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\};\\{\xi _0}\exp (\omega t + ikx);\\{\psi _2}(x,z,t) = \left\{ {\left[ {i({\sigma _1}{E_{10x}} - {\sigma _2}{E_{20x}}) + } \right.} \right.\\ + \left. {({\sigma _1}{E_{20z}} - {\sigma _1}{E_{10z}})\coth (k{h_1})} \right]\sinh \left[ {k(z - {h_2})} \right]/\\/\left\{ {\sinh (k{h_2})\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\};\\{\xi _0}\exp (\omega t - ikx).\end{array}\] | (9) |
Для получения возмущений потенциала течения подставим первое, второе и пятое уравнения системы (6) в кинематические граничные условия (3). В итоге получим:
| \[\begin{array}{c}{\Phi _1}(x,z,t) = \frac{{\omega + ik{U_1}}}{{k\sinh (k{h_1})}} \times \\ \times \cosh \left[ {k(z + {h_1})} \right]{\xi _0}\exp (\omega t + ikx);\\{\Phi _2}(x,z,t) = - \frac{{\omega + ik{U_2}}}{{k\sinh (k{h_2})}} \times \\ \times \cosh \left[ {k(z - {h_2})} \right]{\xi _0}\exp (\omega t + ikx).\end{array}\] | (10) |
Вклад акустического поля в давление будем определять также, как и в работах [14; 15]: psi = ρi geff ξ0 exp(ωt + ikx) (где geff = g – ΩUa cos(Ωt) ‒ эффективное ускорение; Ω и Ua ‒ частота и амплитуда звукового воздействия. Подстановка (9) и (10) в динамическое граничное условие (3) и последующие преобразования c учетом того, что при z = 0: σ1E01z = σ2E02z , E01x = E02x , приводят к следующему дисперсионному уравнению:
| \[\begin{array}{c}{a_0}{\omega ^2} + 2({a_1} + i{b_1})\omega + {a_2} + i{b_2} = 0;\\{a_0} = {\rho _1}\coth (k{h_1}) + {\rho _2}\coth (k{h_2});\\{a_1} = {\rho _1}{\nu _1}{k^2}\coth (k{h_1}) + {\rho _2}{\nu _2}{k^2}\coth (k{h_2});\\{b_1} = {\rho _1}{U_1}k\coth (k{h_1}) + {\rho _2}{U_2}k\coth (k{h_2});\\{a_2} = - {k^2}\left[ {{\rho _1}U_1^2\coth (k{h_1}) + {\rho _2}U_2^2\coth (k{h_2})} \right] + \\ + \gamma {k^3} + \left( {{\rho _1} - {\rho _2}} \right){g_{eff}}k + \\ + {\varepsilon _1}{\varepsilon _0}{k^2}\left[ {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)E_{20x}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}} - } \right.\\ - \left. {\frac{{\sigma _2^2\left( {{\sigma _1} - {\sigma _2}} \right)\coth (k{h_1})\coth (k{h_2})E_{20z}^2}}{{\sigma _1^2\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]}}} \right] + \\ + {\varepsilon _2}{\varepsilon _0}{k^2}\left[ {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)\coth (k{h_1})\coth (k{h_2})E_{20z}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}} - } \right.\\ - \left. {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)E_{20x}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}}} \right];\\{b_2} = \left\{ {{\varepsilon _1}{\varepsilon _0}{k^2}{\sigma _2}\left( {{\sigma _1} - {\sigma _2}} \right)\left[ {\coth (k{h_1}) + \coth (k{h_2})} \right] \times } \right.\\\left. { \times {E_{20x}}{E_{20z}}} \right\}/\left\{ {{\sigma _1}\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\} + \\ + \left\{ {{\varepsilon _2}{\varepsilon _0}{k^2}\left( {{\sigma _1} - {\sigma _2}} \right)\left[ {\coth (k{h_1}) + \coth (k{h_2})} \right]} \right. \times \\\left. { \times {E_{20x}}{E_{20z}}} \right\}/\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right] + \\ + 2{k^3}\left[ {{\rho _1}{\nu _1}{U_1}\coth (k{h_1}) + {\rho _2}{\nu _2}{U_2}\coth (k{h_2})} \right].\end{array}\] | (11) |
Для проведения анализа уравнения (11) с учетом влияния слабых акустических полей воспользуемся подходом, применяемым в работах [14; 15]. Согласно данного подхода:
| \[\begin{array}{c}{a_0}\frac{{{d^2}f}}{{d{t^2}}} + 2({a_1} + i{b_1})\frac{{df}}{{dt}} + ({a_2} + i{b_2})f = 0;\\{a_2} = c - {C_{ac}}\cos (\Omega t);{\rm{ }}\;{C_{ac}} = \left( {{\rho _2} - {\rho _1}} \right)\Omega k{U_a};\\c = - {k^2}\left[ {{\rho _1}U_1^2\coth (k{h_1}) + {\rho _2}U_2^2\coth (k{h_2})} \right] + \gamma {k^3} + \\ + \left( {{\rho _1} - {\rho _2}} \right)gk + {\varepsilon _1}{\varepsilon _0}{k^2}\left[ {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)E_{20x}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2})}} - } \right.\\ - \left. {\frac{{\sigma _2^2\left( {{\sigma _1} - {\sigma _2}} \right)\coth (k{h_1})\coth (k{h_2})E_{20z}^2}}{{\sigma _1^2\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]}}} \right] + \\ + {\varepsilon _2}{\varepsilon _0}{k^2}\left[ {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)\coth (k{h_1})\coth (k{h_2})E_{20z}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}}} \right. - \\ - \left. {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)E_{20x}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}}} \right],\end{array}\] | (12) |
где f – функция, зависящая от времени, является суммой «медленной» компоненты возмущений A1(t) = f1exp(ωt) и «быстрой» компоненты возмущений A2(t) = f2cos(Ωt), которая соответствует звуковым колебаниям; Ω ‒ частота звукового воздействия [14; 15]. Подставляя эту сумму в зависимость (7) и отбрасывая косинусоидальные и синусоидальные члены с учетом того, что f2 = –Cac A1/(a0Ω2) [14], получим:
| \[{a_0}{\omega ^2} + 2\left( {{a_1} + i{b_1}} \right)\omega + c + i{b_2} + \frac{{C_{ac}^2}}{{2{a_0}{\Omega ^2}}} = 0.\] | (13) |
Решение уравнения (7) имеет вид:
| \[\begin{array}{c}{\omega _1} = - \frac{{{a_1} + i{b_1}}}{{{a_0}}} + \\ + \frac{{\sqrt {{{\left( {{a_1} + i{b_1}} \right)}^2} - {a_0}\left( {c + \frac{{C_{ac}^2}}{{2{a_0}{\Omega ^2}}} + i{b_2}} \right)} }}{{{a_0}}};\\{\omega _2} = - \frac{{{a_1} + i{b_1}}}{{{a_0}}} - \\ - \frac{{\sqrt {{{\left( {{a_1} + i{b_1}} \right)}^2} - {a_0}\left( {c + \frac{{C_{ac}^2}}{{2{a_0}{\Omega ^2}}} + i{b_2}} \right)} }}{{{a_0}}}.\end{array}\] | (14) |
Второй корень уравнения (8) не имеет физического смысла и поэтому здесь не рассматривается. Скорость роста возмущений поверхности раздела жидкостей найдем как α = Re(ω1). В итоге получим:
| \[\begin{array}{c}\alpha = - \frac{{{a_1}}}{{{a_0}}} + \frac{1}{{2{a_0}}}\left[ {2(a_1^2 + b_1^2 - {a_0}) - \frac{{C_{ac}^2}}{{{\Omega ^2}}} + } \right.\\ + {\left. {2\sqrt {{{\left( {a_1^2 + b_1^2 - {a_0}c - \frac{{C_{ac}^2}}{{2{\Omega ^2}}}} \right)}^2} + {{(2{a_1}{b_1} - {b_2}{a_0})}^2}} } \right]^{1/2}}.\end{array}\] | (15) |
Данные для расчетов по формуле (9) представлены в таблице.
Характеристики материалов и параметры внешнего воздействия
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Результаты исследования и их обсуждение
Система воздух – вода
На рис. 2, а представлены зависимости скорости роста возмущений поверхности раздела воздуха и воды от волнового числа в отсутствие звукового поля при воздействии электрических полей; разность горизонтальных скоростей слоев составляла 15 м/с. Данная функция имеет только один максимум вне зависимости от наличия электрического поля (кривые 1 – 3). Тангенциальное электрическое поле (β = 0) напряженностью порядка 3·106 В/м приводит к стабилизации неустойчивости Кельвина–Гельмгольца, что выражается в снижении значений αm и смещении максимальной моды km в сторону меньших значений (кривая 2). Нормальное электрическое поле (β = π/2) такой же напряженностью, наоборот, усиливает данную неустойчивость (кривая 3), что соответствует общепринятым представлениям [8; 19]. При углах наклона вектора электрического поля β π/6, π/4, π/3 (рис. 2, б) наблюдается увеличение значений km от 59 170 м–1 (λm = 106,19 мкм) при β = π/6 до 119 709 м–1 (λm = 52,48 мкм) при β = π/3. Анализ нейтральных кривых (рис. 2, в) показал, что наличие вертикальной компоненты электрического поля значительно сужает диапазон относительной скорости движения сред, в котором капиллярные силы и тангенциальное электрическое поле подавляют неустойчивость Кельвина–Гельмгольца. Следует отметить, что подобный эффект наблюдался в работе [8] для случая невязких диэлектрических жидкостей.
Рис. 2. Зависимости скорости роста возмущений поверхности раздела воздух – вода (а, б) |
Рассмотрим совместное влияние слабых акустических и наклонных электрических полей на неустойчивость Кельвина–Гельмгольца. На рис. 3, а показаны зависимости скорости роста возмущений при амплитудном значении скорости звуковых колебаний Ua = 5 м/с. Эти зависимости показывают, что звуковые колебания приводят к подавлению неустойчивости Кельвина–Гельмгольца (кривые 1 – 3), при этом тангенциальное электрическое поле усиливает данный эффект (кривая 2), а нормальное поле, наоборот, ослабляет его. Ослабление эффекта подавления также наблюдается и при углах наклона поля β π/6, π/4, π/3 (рис. 3, б), что подтверждает анализ нейтральных кривых (рис. 3, в). Отметим, что подобные явления подавления неустойчивости Кельвина–Гельмгольца обнаружены в работе [14]. Однако в этом исследовании наложение звуковых полей приводит к смещению km вправо, при этом максимальная скорость роста увеличивается, что говорит об усилении неустойчивости Кельвина–Гельмгольца. Такое различие данных работы [14] и настоящей работы может быть объяснено тем, что в ней соотношение \(\frac{{C_{ac}^2}}{{2{a_0}{\Omega ^2}}}\) в формуле (8) бралось с отрицательным знаком, а в настоящей работе – с положительным.
Рис. 3. Зависимости скорости роста возмущений поверхности раздела воздух – вода (а, б) |
Система аргон – железо
Рассмотрим теперь другую ситуацию, возникающую в процессах наплавки или сварки. В этих процессах при расплавлении электрода в среде защитного газа аргона возникает струя жидкого металла, которая при определенных условиях распадается на капли [20]. От режима переноса материала зависит качество сформированного покрытия, поэтому разработка способов управления этим процессом является важной задачей. В этой системе при взаимном течении газа и жидкости возникает неустойчивость Кельвина–Гельмгольца. На рис. 4, а приведены дисперсионные кривые, из которых видно, что они имеют два максимума. Первый максимум, согласно работе [13], является гидродинамическим, а второй обусловлен вязкостью (кривая 1).
Рис. 4. Зависимости скорости роста возмущений поверхности раздела аргон – железо (а – в) |
Приложение тангенциального поля напряженностью 3·107 В/м приводит к практически полному подавлению гидродинамического максимума (кривая 2), тогда как в нормальном поле этот эффект слабее (кривая 3). Как показывают результаты [19], смена знака влияния поперечного электрического поля на капиллярную неустойчивость связана с соотношением удельных электрических проводимостей σ = σ2 /σ1 и диэлектрических проницаемостей сред ε = ε2 /ε1 . Если ε > σ, то мы имеем дело со стабилизирующим эффектом воздействия электрического поля, в противном случае (ε < σ) электрическое поле оказывает дестабилизирующее влияние [19]. В рассматриваемом случае (см. таблицу) для системы аргон – железо σ ~ 0,00133, а ε ~ 0,0002, что должно говорить о дестабилизирующем влиянии нормального поля. Но это не так (рис. 4, а). Такое расхождение с капиллярной неустойчивостью может быть объяснено тем, что в рассматриваемом случае значимой становится относительная скорость течения слоев, которая изменяет условие возникновения максимумов неустойчивости Кельвина–Гельмгольца [21]. Дальнейшее увеличение соотношения удельных электрических проводимостей σ до значения больше 0,012 приводит к восстановлению гидродинамического максимума и полному подавлению вязкостно-обусловленного, а при σ ≥ 0,015 происходит смена знака эффекта со стабилизирующего на дестабилизирующий (рис. 4, б). Результаты изучения влияния наклонных электрических полей (рис. 4, в) показали, что данные поля усиливают неустойчивость Кельвина–Гельмгольца вне зависимости от значения соотношений σ и ε. При этом максимум скорости роста является вязкостно-обусловленным. При значениях напряженности поля E20x < 3·107 В/м наблюдается слабовыраженный гидродинамический максимум (рис. 4, г). Кривые нейтральной устойчивости показывают, что, как и в случае системы воздух – вода, наблюдается уменьшение области стабильности возмущений поверхности раздела (рис. 4, д).
Совместное воздействие акустических колебаний с амплитудой скорости 10 м/с и электрического поля напряженностью 3·107 В/м при σ ~ 0,00133, а ε ~ 0,0002, наоборот, приводит к полному подавлению вязкостно-обусловленного максимума неустойчивости (рис. 5, а, кривая 1) и к резкому снижению максимальной скорости роста αm возмущений гидродинамического происхождения. Приложение горизонтального электрического поля значительно ослабляет этот эффект (рис. 5, а, кривая 2), а в вертикальном поле этот эффект, наоборот, усиливается (рис. 5, а, кривая 3) несмотря на то, что, при E20x = 0 и E20z = 3·107 В/м значение km больше, чем при E20x = 3·107 В/м и E20z = 0. Смена знака эффекта на дестабилизирующий также происходит при σ ≥ 0,015 (рис. 5, б). Приложение наклонного электрического поля, также как и в отсутствие звука, усиливает неустойчивость Кельвина–Гельмгольца, но αm несколько меньше (рис. 5, в). Нейтральные кривые (рис. 5, г) показывают увеличение диапазона скоростей сред, в которых капиллярные силы и тангенциальные поля подавляют неустойчивость Кельвина–Гельмгольца при воздействии акустического поля.
Рис. 5. Зависимости скорости роста возмущений поверхности раздела аргон – железо (а – в) |
Выводы
Наклонные электрические поля способствуют усилению неустойчивости Кельвина–Гельмгольца на границах раздела проводящих сред вне зависимости от соотношения их плотностей, удельных электрических проводимостей и наличия звуковых полей.
Установлено, что совместное применение наклонных электрических полей и акустических колебаний в системе воздух – вода позволяет получать капли жидкости в диапазоне от 10 до 100 мкм даже при малых скоростях движения газа. Это открывает новые перспективы для разработки технологий ускоренного охлаждения проката, для достижения его высокой твердости и ударной вязкости.
Для системы аргон – железо показано, что вертикальное электрическое поле при значениях σ ~ 10–3 и ε ~ 10–4 приводит практически к подавлению гидродинамического максимума. Увеличение соотношения удельных электрических проводимостей σ до значения более 0,012, наоборот, приводит к восстановлению гидродинамического максимума и полному подавлению вязкостно-обусловленного. При σ ≥ 0,015 происходит смена знака эффекта со стабилизирующего на дестабилизирующий вне зависимости от количества максимумов зависимости скорости роста от длины волны. При воздействии тангенциального электрического поля неустойчивость Кельвина–-Гельмгольца полностью подавляется.
Совместное воздействие звуковых колебаний и нормального электрического поля приводит к полному подавлению вязкостно-обусловленного максимума неустойчивости и резкому снижению максимальной скорости роста возмущений гидродинамического происхождения, при этом в горизонтальном электрическом поле этот эффект проявляется значительно слабее.
Список литературы
1. Praturi D.S., Girimaji S.S. Mechanisms of canonical Kelvin-Helmholtz instability suppression in magnetohydrodynamic flows. Physics of Fluids. 2019;31(2):024108. https://doi.org/10.1063/1.5083857
2. Rahmani M., Seymour B.R., Lawrence G.A. The effect of Prandtl number on mixing in low Reynolds number Kelvin-Helmholtz billows. Physics of Fluids. 2016;28(5):054107. https://doi.org/10.1063/1.4949267
3. Panin V.E., Gromov V.E., Romanov D.A., Budovskikh E.A., Panin S.V. The physical basics of structure formation in electroexplosive coatings. Doklady Physics. 2017;62:67‒70. https://doi.org/10.1134/S1028335817020112
4. Mishin V.V., Tomozov V.M. Kelvin–Helmholtz instability in the solar atmosphere, solar wind and geomagnetosphere. Solar Physics. 2016;291:3165‒3184. https://doi.org/10.1007/s11207-016-0891-4
5. Petrarolo A., Kobald M., Schlechtriem S. Understanding Kelvin–Helmholtz instability in paraffin-based hybrid rocket fuels. Experiments in Fluids. 2018;59:62. https://doi.org/10.1007/s00348-018-2516-1
6. Григорьев А.И., Ширяев А.А., Ширяева С.О. Неустойчивость заряженной капли в неоднородном электростатическом поле стержня конечной толщины. Известия РАН. Механика жидкости и газа. 2018;(1):36‒50. https://doi.org/10.7868/S0568528118010048
7. Saraev Yu.N., Chinakhov D.A., Ilyashchenko D.I., Kiselev A.S., Gordynets A.S. Investigation of the stability of melting and electrode metal transfer in consumable electrode arc welding using power sources with different dynamic characteristics. Welding International. 2017;31(10):784–790. https://doi.org/10.1080/09507116.2017.1343977
8. Korovin V.M. Effect of tilted electrostatic field on the Kelvin–Helmholtz instability in a liquid dielectric and gas flow. Technical Physics. 2017;62:1316‒321. https://doi.org/10.1134/S1063784217090134
9. Сарычев В.Д., Хаимзон Б.Б., Невский С.А., Ильященко А.В., Гришунин В.А. Математические модели механизмов ускоренного охлаждения проката. Известия вузов. Черная металлургия. 2018;61(4):326–332. https://doi.org/10.17073/0368-0797-2018-4-326-332
10. Awasthi M.K., Asthana R., Agrawal G.S. Viscous correction for the viscous potential flow analysis of Kelvin–Helmholtz instability of cylindrical flow with heat and mass transfer. International Journal of Heat and Mass Trans. 2014;78:251‒259. https://doi.org/10.1016/j.ijheatmasstransfer.2014.06.082
11. Barreras F., Lozano A., Dopazo C. Linear instability analysis of the viscous longitudinal perturbation on an air-blasted liquid sheet. Atomization and Sprays. 2001;11(2):139‒154. https://doi.org/10.1615/ATOMIZSPR.V11.I2.30
12. Logvinov O.A. Linear stability of stratified flow of two viscous fluids. Moscow University Mechanics Bulletin. 2022;77; 117–126. https://doi.org/10.3103/S0027133022040021
13. Sarychev V.D., Granovskii A.Yu., Gromov V.E. Model of formation of inner nanolayers in shear flows of material. Technical Physics. 2013;58(10):1544‒157. https://doi.org/10.1134/S1063784213100113
14. Bychkov V. Analytical scalings for flame interaction with sound waves. Physics of Fluids. 1999;11(10):3168‒3173. https://doi.org/10.1063/1.870173
15. Bilgili S., Ugarte O., Akkerman V. Interplay of Kelvin–Helmholtz instability with acoustics in a viscous potential flow. Physics of Fluids. 2020;32(8):084108. https://doi.org/10.1063/5.0017448
16. Awasthi M.K., Dutt N., Kumar A., Kumar S. Electrohydrodynamic capillary instability of Rivlin–Ericksen viscoelastic fluid film with mass and heat transfer. Heat Transfer. 2024;53(1):115–133. https://doi.org/10.1002/htj.22944
17. Saville D.A. Electrohydrodynamic stability: effects of charge relaxation at the interface of a liquid jet. Journal of Fluid Mechanics. 1971;48(4):815–827. https://doi.org/10.1017/S0022112071001873
18. Shkadov V.Ya., Shutov A.A. Stability of a surface-charged viscous jet in an electric field. Fluid Dynamics. 1998;33(2):176–185. https://doi.org/10.1007/BF02698699
19. Awasthi M.K. Study on electrohydrodynamic capillary instability of viscoelastic fluids with radial electric field. International Journal of Applied Mechanics. 2014;6(4):1450037. https://doi.org/10.1142/S1758825114500379
20. Zhao Y., Chung H. Numerical simulation of droplet transfer behavior in variable polarity gas metal arc welding. International Journal of Heat and Mass Transfer. 2017;111:1129‒1141. https://doi.org/10.1016/j.ijheatmasstransfer.2017.04.090
21. Невский С.А., Сарычев В.Д., Грановский А.Ю., Бащенко Л.П., Громов В.Е. Формирование микро- и наноструктур при электровзрывном карбоборировании титановых сплавов по механизму гидродинамических неустойчивостей. Фундаментальные проблемы современного материаловедения. 2023;20(3):317–328. https://doi.org/10.25712/ASTU.1811-1416.2023.03.004
Об авторах
С. А. НевскийРоссия
Сергей Андреевич Невский, д.т.н., доцент кафедры естественнонаучных дисциплин им. профессора В.М. Финкеля
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Л. П. Бащенко
Россия
Людмила Петровна Бащенко, к.т.н., доцент кафедры теплоэнергетики и экологии
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
В. Д. Сарычев
Россия
Владимир Дмитриевич Сарычев, к.т.н., доцент кафедры естественнонаучных дисциплин им. профессора В.М. Финкеля
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
А. Ю. Грановский
Россия
Алексей Юрьевич Грановский, к.т.н., старший научный сотрудник Управления научных исследований
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Д. В. Шамсутдинова
Россия
Диана Витальевна Шамсутдинова, студент Института педагогического образования
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Рецензия
Для цитирования:
Невский С.А., Бащенко Л.П., Сарычев В.Д., Грановский А.Ю., Шамсутдинова Д.В. Влияние наклонного электрического поля на распад струи жидкости в процессах термообработки и наплавки. Известия высших учебных заведений. Черная Металлургия. 2025;68(1):30-39. https://doi.org/10.17073/0368-0797-2025-1-30-39
For citation:
Nevskii S.A., Bashchenko L.P., Sarychev V.D., Granovskii A.Yu., Shamsutdinova D.V. Influence of inclined electric field on decay of a liquid jet during heat treatment and surfacing. Izvestiya. Ferrous Metallurgy. 2025;68(1):30-39. https://doi.org/10.17073/0368-0797-2025-1-30-39
JATS XML