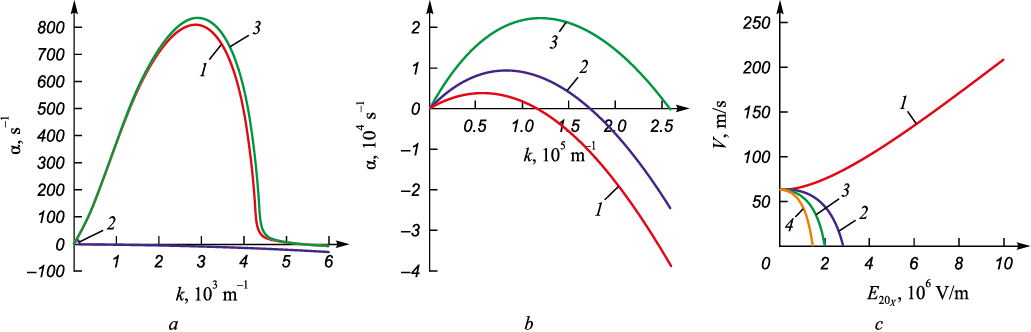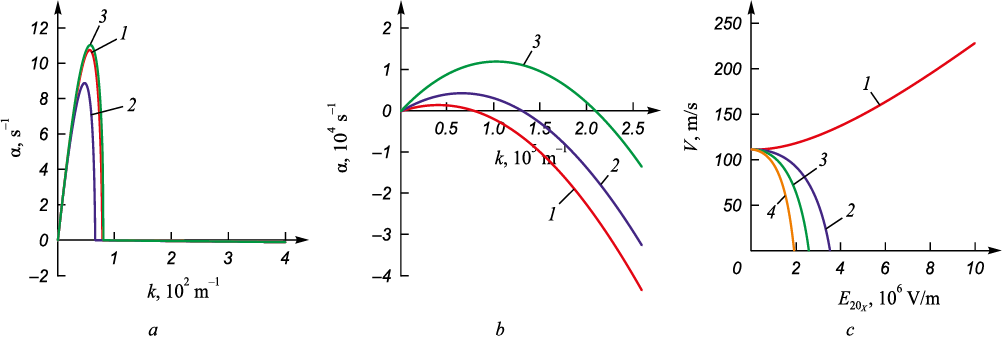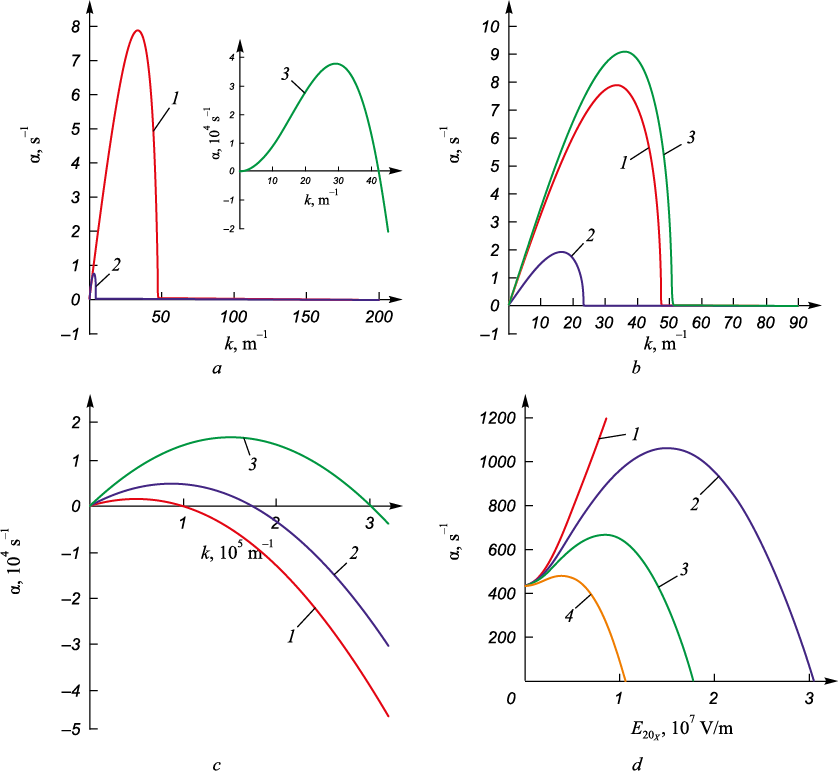Scroll to:
Influence of inclined electric field on decay of a liquid jet during heat treatment and surfacing
https://doi.org/10.17073/0368-0797-2025-1-30-39
Abstract
The combined effect of inclined electric fields and a transverse acoustic field on the Kelvin–Helmholtz instability of the interface of viscous electrically conductive liquids is studied using the example of air – water and argon – iron systems. An inclined electric field, regardless of the effect of sound vibrations, leads to the increased Kelvin–Helmholtz instability in the micrometer wavelength range. The most intense increase in the disturbances of the interface is observed at the angle of inclination of the electric field π/3. This opens up new opportunities for the development of technologies for accelerated cooling of rolled products and surfacing materials by regulating the drop transfer of material. The combined effect of acoustic and electric fields has an ambiguous effect on the Kelvin–Helmholtz instability. In the case of an air – water system, sound vibrations lead to suppression of the Kelvin–Helmholtz instability, while a tangential electric field with a strength of 3·106 V/m enhances this effect, and a normal field, on the contrary, weakens it. For the argon – iron system, sound vibrations lead to the complete disappearance of the viscosity-conditioned maximum and to a significant decrease in the growth rate of disturbances at the interface, which corresponds to the first maximum. Application of a horizontal electric field with a strength of 3·107 V/m significantly weakens the effect of suppressing the Kelvin–Helmholtz instability, while in a vertical field, on the contrary, increases it. It was established that the restoration of the first hydrodynamic maximum in a normal electric field is possible with a ratio of specific electrical conductivities σ greater than 0.012, regardless of the presence of a sound field. A change in the influence of the vertical electric field from a stabilizing to a destabilizing one is possible with a ratio of σ from 0.015 or more.
Keywords
For citations:
Nevskii S.A., Bashchenko L.P., Sarychev V.D., Granovskii A.Yu., Shamsutdinova D.V. Influence of inclined electric field on decay of a liquid jet during heat treatment and surfacing. Izvestiya. Ferrous Metallurgy. 2025;68(1):30-39. https://doi.org/10.17073/0368-0797-2025-1-30-39
Introduction
The Kelvin–Helmholtz instability occurs in various research fields, ranging from terrestrial magnetohydrodynamics [1] and turbulent liquid mixing [2] to processes such as coating deposition by electrical explosion [3] and astrophysical phenomena like the solar wind [4]. This instability serves as a powerful trigger that disrupts the stability of systems involving the mixing of two or more liquids with different properties. Some of the most notable applications of this instability include acoustic modes in air-consuming systems such as boilers, jet engines, and gas turbines [5]. Another significant application of this instability is the breakup of a liquid jet into droplets in an electric field [6; 7]. This phenomenon underlies the operation of precision devices that are integral to various technological processes, such as electric arc welding and the production of ultrafine refractory powders [6; 7]. In [8], the influence of an inclined electric field on the Kelvin–Helmholtz instability of two ideal dielectric liquids was studied, revealing the conditions under which the liquid transitions to a stable mode under a horizontal electric field. It was also demonstrated that the vertical component of the electric field exerts a destabilizing effect. Another promising application of this instability is the accelerated cooling of rolled products. In [9], it was shown that by controlling the velocity of the air – water system, it is possible to achieve the formation of droplets in the nanometer range. Upon impacting rolled products, these droplets induce a thermoelastic wave, thereby increasing their impact toughness.
The origin and development of the Kelvin–Helmholtz instability of two viscous liquids were investigated in [10; 11]. A key feature of these studies is the use of the viscous potential approximation. This approach assumes the absence of shear stress components of the stress tensor at the interface, while the viscosity of the liquid is taken into account only in the condition of continuity of normal stresses at the interface [10]. In the general case, the situation is complicated by the need to determine the velocity profile of the fluid, and as shown in [11; 12], there is no analytical solution for the stability of a flow with a complex velocity profile. However, at high wavenumbers (short wavelengths), this approximation is justified, as demonstrated in.
The interaction of the Kelvin–Helmholtz instability with ultrasonic vibrations in the case of a problem with planar geometry under the viscous potential flow approximation was studied in [14; 15]. The interaction of the Kelvin–Helmholtz instability with ultrasonic vibrations in a planar geometry under the viscous potential approximation was studied in [14; 15]. It was assumed that the effect of acoustic vibrations is equivalent to an effective oscillating gravitational field. It was found that acoustic influence shifts the maximum growth rate toward higher wavenumbers [15], and a stability region was identified between weak acoustic excitation and parametric resonance.
The objective of this study was to investigate the combined influence of an inclined electric field and a transverse acoustic field on the stability of the planar surface of an electrically conductive liquid using the example of the iron – argon and air – water systems under the viscous potential flow approximation. The simultaneous application of these two factors enables the creation of micro- and nanodroplet flow patterns, which is crucial for the development of new technologies in welding, surfacing, and accelerated cooling of rolled products.
Problem statement
Consider the instability of the planar interface between two viscous electrically conductive fluids. The first fluid is characterized by density ρ1 , kinematic viscosity ν1 , electrical conductivity σ1 , and dielectric permittivity ε1 (Fig. 1). It occupies the region (–∞ ≤ x ≤ +∞ and –h1 ≤ z ≤ 0) and moves with a horizontal velocity U1 . The second fluid occupies the region (–∞ ≤ x ≤ +∞ and 0 ≤ z ≤ h2 ) and is characterized by density ρ2 , kinematic viscosity ν2 , electrical conductivity σ2 , and dielectric permittivity ε2 . The horizontal velocity of the second fluid is U2 . The variable ξ represents the deviation of the interface from its equilibrium position (Fig. 1).
Fig. 1. On formulation of the problem of origin and development |
The flow velocities of the first and second fluids are much lower than the speed of sound; therefore, they can be considered incompressible. The kinematics of the interface motion is described by the function F(x, z, t) = z – ξ(x, t). Thus \(\vec n = \frac{{\nabla F}}{{\left| {\nabla F} \right|}} = \frac{{ - \frac{{\partial \xi }}{{\partial x}}{{\vec e}_x} + {{\vec e}_z}}}{{\sqrt {1 + {{\left( {\frac{{\partial \xi }}{{\partial x}}} \right)}^2}} }}\) the normal vector is defined as (where \(\nabla \) is the gradient operator. In the linear approximation, the normal vector \(\vec n = - \frac{{\partial \xi }}{{\partial x}}{\vec e_x} + {\vec e_z}\). takes the form. The system under consideration is placed in an external transverse acoustic field and an inclined electric field relative to the planar interface of the fluid (Fig. 1). The electric field vector, taking into account the disturbances of the interface, is given by \(\vec E = {E_{0x}}{\vec e_x} - {E_{0z}}{\vec e_z} - \nabla \psi \) (where ψ is the disturbance of the electric potential, and E0x and E0z are the normal and tangential components of the unperturbed electric field, respectively). The inclination angle of the electric field (Fig. 1) relative to the unperturbed surface β is defined as \({\rm{arctg}}\left( {\frac{{{E_{0z}}}}{{{E_{0x}}}}} \right)\).
The fundamental linearized equations of the viscous potential flow model for relatively small disturbances, taking into account the electric field, according to [10; 15], are given as:
| \[\begin{array}{c}\Delta {\Phi _1} = 0;{\rm{ }} - {h_1} < z < 0;{\rm{ }}\\\Delta {\Phi _2} = 0;{\rm{ }}0 < r < {h_2};\\\Delta {\psi _1} = 0;{\rm{ }} - {h_1} < z < 0;{\rm{ }}\\\Delta {\psi _2} = 0;{\rm{ }}0 < r < {h_2},\end{array}\] | (1) |
where Φ is represents the velocity potential disturbance.
When deriving the first and second equations of system (1), the terms associated with the electric field were neglected, which is valid for electrically conductive liquids [16 ‒ 18], in the absence of a volumetric charge. Therefore, the electric field component will only be considered in the boundary conditions at the liquid–gas interface. At the boundaries h2 and h1 , we impose conditions ensuring the absence of disturbances in the flow velocity and the electric field:
| \[\begin{array}{l}z = - {h_1}:{\rm{ }}\;\frac{{\partial {\Phi _1}}}{{\partial z}} = 0;{\rm{ }}\;\frac{{\partial {\psi _1}}}{{\partial x}} = 0;{\rm{ }}\\{\rm{ }}z = {h_2}:{\rm{ }}\;\frac{{\partial {\Phi _2}}}{{\partial z}} = 0;{\rm{ }}\;\frac{{\partial {\psi _2}}}{{\partial x}} = 0.\end{array}\] | (2) |
The boundary conditions for the disturbances of the flow potential of the liquid at the interface, taking into account the electric field, are given by:
| \[\begin{array}{c}z = 0:{\rm{ }}\;\frac{{\partial {\Phi _1}}}{{\partial z}} = \frac{{\partial \xi }}{{\partial t}} + {U_1}\frac{{\partial \xi }}{{\partial z}};{\rm{ }}\;\frac{{\partial {\Phi _2}}}{{\partial z}} = \frac{{\partial \xi }}{{\partial t}} + {U_2}\frac{{\partial \xi }}{{\partial z}};{\rm{ }}\\ - {p_1} + 2{\rho _1}{\nu _1}\frac{{{\partial ^2}{\Phi _1}}}{{\partial {z^2}}} + {p_{s1}} - \frac{1}{2}{\varepsilon _1}{\varepsilon _0}\left( {E_{1n}^2 - E_{1\tau }^2} \right) + \\ + {p_2} - 2{\rho _2}{\nu _2}\frac{{{\partial ^2}{\Phi _2}}}{{\partial {z^2}}} - {p_{s2}} + \frac{1}{2}{\varepsilon _2}{\varepsilon _0}\left( {E_{2n}^2 - E_{2\tau }^2} \right) = \gamma \frac{{{\partial ^2}\xi }}{{\partial {x^2}}},\end{array}\] | (3) |
where Ui is the velocity of the i-th fluid; \({p_i} = - {\rho _i}\left( {\frac{{\partial {\Phi _i}}}{{\partial t}} + {U_i}\frac{{\partial {\Phi _i}}}{{\partial x}}} \right)\) is the pressure disturbance in the i-th fluid; psi is the disturbance of the pressure of the acoustic field; i = 1, 2 is the fluid index; γ is the surface tension; Ein and Eiτ are the normal and tangential components of the field, respectively.
The boundary conditions for the electric field at the interface are defined as [19]:
| \[\vec n \cdot {\vec E_1} = \vec n \cdot {\vec E_2};{\rm{ }}{\sigma _1}\left( {\vec n \cdot {{\vec E}_1}} \right) = {\sigma _2}\left( {\vec n \cdot {{\vec E}_2}} \right).\] | (4) |
Substituting the above values of the normal vector and the electric field into equation (4) and subsequently linearizing, taking into account that at the interface of two conductors σ1E01z = σ2E02z , and E01x = E02x , leads to the following:
| \[\begin{array}{c}{E_{10z}}\frac{{\partial \xi }}{{\partial x}} + \frac{{\partial {\psi _1}}}{{\partial x}} = {E_{20z}}\frac{{\partial \xi }}{{\partial x}} + \frac{{\partial {\psi _2}}}{{\partial x}};{\rm{ }}\\{\sigma _1}\left( {{E_{10x}}\frac{{\partial \xi }}{{\partial x}} + \frac{{\partial {\psi _1}}}{{\partial z}}} \right) = {\sigma _2}\left( {{E_{20x}}\frac{{\partial \xi }}{{\partial x}} + \frac{{\partial {\psi _2}}}{{\partial z}}} \right).\end{array}\] | (5) |
The solution to equations (1) will be sought in the form:
| \[\begin{array}{c}{\Phi _1}(x,z,t) = {A_1}\cosh \left[ {k(z + {h_1})} \right]\exp (\omega t + ikx);\\{\Phi _2}(x,z,t) = {A_2}\cosh \left[ {k(z - {h_2})} \right]\exp (\omega t + ikx);\\{\psi _1}(x,z,t) = {A_3}\sinh \left[ {k(z + {h_1})} \right]\exp (\omega t + ikx);\\{\psi _2}(x,z,t) = {A_4}\sinh \left[ {k(z - {h_2})} \right]\exp (\omega t + ikx);\\\xi (x,t) = {\xi _0}\exp (\omega t + ikx).\end{array}\] | (6) |
Substituting the third, fourth, and fifth equations of (6) into equation (5) leads to the following system of equations for the constants A3 and A4 :
| \[\begin{array}{c}{A_3}\sinh (k{h_1}) + {A_4}\sinh (k{h_2}) = \left( {{E_{20z}} - {E_{10z}}} \right){\xi _0};\\{A_3}{\sigma _1}\cosh (k{h_1}) - {A_4}{\sigma _2}\cosh (k{h_2}) = \\ = i{\xi _0}\left( {{\sigma _2}{E_{20x}} - {\sigma _1}{E_{10x}}} \right).\end{array}\] | (7) |
The solution to system (7) after transformation takes the form:
| \[\begin{array}{c}{A_3} = - \left\{ {\left[ {i\left( {{\sigma _1}{E_{10x}} - {\sigma _2}{E_{20x}}} \right) + \left( {{\sigma _2}{E_{10z}} - {\sigma _2}{E_{20z}}} \right)} \right. \times } \right.\\ \times \left. {\left. {\coth (k{h_2})} \right]{\xi _0}} \right\} \times \\ \times {\left\{ {\sinh (k{h_1})\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\}^{ - 1}};\\{A_4} = - \left\{ {\left[ {i\left( {{\sigma _1}{E_{10x}} - {\sigma _2}{E_{20x}}} \right) + \left( {{\sigma _1}{E_{20z}} - {\sigma _1}{E_{10z}}} \right)} \right. \times } \right.\\ \times \left. {\left. {\coth (k{h_1})} \right]{\xi _0}} \right\} \times \\ \times {\left\{ {\sinh (k{h_2})\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\}^{ - 1}}.\end{array}\] | (8) |
Then, the disturbances of the electric potential will take the following form:
| \[\begin{array}{c}{\psi _1}(x,z,t) = - \left\{ {\left[ {i({\sigma _1}{E_{10x}} - {\sigma _2}{E_{20x}}) + } \right.} \right.\\ + \left. {({\sigma _2}{E_{10z}} - {\sigma _2}{E_{20z}})\coth (k{h_2})} \right]\sinh \left[ {k(z + {h_1})} \right]/\\/\left\{ {\sinh (k{h_1})\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\};\\{\xi _0}\exp (\omega t + ikx);\\{\psi _2}(x,z,t) = \left\{ {\left[ {i({\sigma _1}{E_{10x}} - {\sigma _2}{E_{20x}}) + } \right.} \right.\\ + \left. {({\sigma _1}{E_{20z}} - {\sigma _1}{E_{10z}})\coth (k{h_1})} \right]\sinh \left[ {k(z - {h_2})} \right]/\\/\left\{ {\sinh (k{h_2})\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\};\\{\xi _0}\exp (\omega t - ikx).\end{array}\] | (9) |
To derive the disturbances of the flow potential, we substitute the first, second, and fifth equations of system (6) into the kinematic boundary conditions (3). As a result, we obtain:
| \[\begin{array}{c}{\Phi _1}(x,z,t) = \frac{{\omega + ik{U_1}}}{{k\sinh (k{h_1})}} \times \\ \times \cosh \left[ {k(z + {h_1})} \right]{\xi _0}\exp (\omega t + ikx);\\{\Phi _2}(x,z,t) = - \frac{{\omega + ik{U_2}}}{{k\sinh (k{h_2})}} \times \\ \times \cosh \left[ {k(z - {h_2})} \right]{\xi _0}\exp (\omega t + ikx).\end{array}\] | (10) |
The contribution of the acoustic field to the pressure is determined in the same way as in [14; 15]: psi = ρi geff ξ0 exp(ωt + ikx) (where geff = g – ΩUa cos(Ωt) is the effective acceleration; Ω and Ua are the frequency and amplitude of the acoustic excitation. Substituting (9) and (10) into the dynamic boundary condition (3) and performing subsequent transformations, taking into account that at z = 0: σ1E01z = σ2E02z , E01x = E02x , leads to the following dispersion equation:
| \[\begin{array}{c}{a_0}{\omega ^2} + 2({a_1} + i{b_1})\omega + {a_2} + i{b_2} = 0;\\{a_0} = {\rho _1}\coth (k{h_1}) + {\rho _2}\coth (k{h_2});\\{a_1} = {\rho _1}{\nu _1}{k^2}\coth (k{h_1}) + {\rho _2}{\nu _2}{k^2}\coth (k{h_2});\\{b_1} = {\rho _1}{U_1}k\coth (k{h_1}) + {\rho _2}{U_2}k\coth (k{h_2});\\{a_2} = - {k^2}\left[ {{\rho _1}U_1^2\coth (k{h_1}) + {\rho _2}U_2^2\coth (k{h_2})} \right] + \\ + \gamma {k^3} + \left( {{\rho _1} - {\rho _2}} \right){g_{eff}}k + \\ + {\varepsilon _1}{\varepsilon _0}{k^2}\left[ {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)E_{20x}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}} - } \right.\\ - \left. {\frac{{\sigma _2^2\left( {{\sigma _1} - {\sigma _2}} \right)\coth (k{h_1})\coth (k{h_2})E_{20z}^2}}{{\sigma _1^2\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]}}} \right] + \\ + {\varepsilon _2}{\varepsilon _0}{k^2}\left[ {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)\coth (k{h_1})\coth (k{h_2})E_{20z}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}} - } \right.\\ - \left. {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)E_{20x}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}}} \right];\\{b_2} = \left\{ {{\varepsilon _1}{\varepsilon _0}{k^2}{\sigma _2}\left( {{\sigma _1} - {\sigma _2}} \right)\left[ {\coth (k{h_1}) + \coth (k{h_2})} \right] \times } \right.\\\left. { \times {E_{20x}}{E_{20z}}} \right\}/\left\{ {{\sigma _1}\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]} \right\} + \\ + \left\{ {{\varepsilon _2}{\varepsilon _0}{k^2}\left( {{\sigma _1} - {\sigma _2}} \right)\left[ {\coth (k{h_1}) + \coth (k{h_2})} \right]} \right. \times \\\left. { \times {E_{20x}}{E_{20z}}} \right\}/\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right] + \\ + 2{k^3}\left[ {{\rho _1}{\nu _1}{U_1}\coth (k{h_1}) + {\rho _2}{\nu _2}{U_2}\coth (k{h_2})} \right].\end{array}\] | (11) |
To analyze equation (11) while considering the influence of weak acoustic fields, we adopt the approach used in [14; 15]. According to this method:
| \[\begin{array}{c}{a_0}\frac{{{d^2}f}}{{d{t^2}}} + 2({a_1} + i{b_1})\frac{{df}}{{dt}} + ({a_2} + i{b_2})f = 0;\\{a_2} = c - {C_{ac}}\cos (\Omega t);{\rm{ }}\;{C_{ac}} = \left( {{\rho _2} - {\rho _1}} \right)\Omega k{U_a};\\c = - {k^2}\left[ {{\rho _1}U_1^2\coth (k{h_1}) + {\rho _2}U_2^2\coth (k{h_2})} \right] + \gamma {k^3} + \\ + \left( {{\rho _1} - {\rho _2}} \right)gk + {\varepsilon _1}{\varepsilon _0}{k^2}\left[ {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)E_{20x}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2})}} - } \right.\\ - \left. {\frac{{\sigma _2^2\left( {{\sigma _1} - {\sigma _2}} \right)\coth (k{h_1})\coth (k{h_2})E_{20z}^2}}{{\sigma _1^2\left[ {\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}} \right]}}} \right] + \\ + {\varepsilon _2}{\varepsilon _0}{k^2}\left[ {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)\coth (k{h_1})\coth (k{h_2})E_{20z}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}}} \right. - \\ - \left. {\frac{{\left( {{\sigma _1} - {\sigma _2}} \right)E_{20x}^2}}{{\coth (k{h_1}){\sigma _1} + \coth (k{h_2}){\sigma _2}}}} \right],\end{array}\] | (12) |
where f is a time-dependent function and represents the sum of a “slow” disturbance component A1(t) = f1exp(ωt), and a “fast” disturbance component, A2(t) = f2cos(Ωt), which corresponds to acoustic vibrations. Here Ω is the frequency of the acoustic influence [14; 15]. Substituting this sum into equation (7) and discarding the cosine and sine terms, considering that f2 = –Cac A1/(a0Ω2) [14], we obtain:
| \[{a_0}{\omega ^2} + 2\left( {{a_1} + i{b_1}} \right)\omega + c + i{b_2} + \frac{{C_{ac}^2}}{{2{a_0}{\Omega ^2}}} = 0.\] | (13) |
The solution of equation (7) takes the form:
| \[\begin{array}{c}{\omega _1} = - \frac{{{a_1} + i{b_1}}}{{{a_0}}} + \\ + \frac{{\sqrt {{{\left( {{a_1} + i{b_1}} \right)}^2} - {a_0}\left( {c + \frac{{C_{ac}^2}}{{2{a_0}{\Omega ^2}}} + i{b_2}} \right)} }}{{{a_0}}};\\{\omega _2} = - \frac{{{a_1} + i{b_1}}}{{{a_0}}} - \\ - \frac{{\sqrt {{{\left( {{a_1} + i{b_1}} \right)}^2} - {a_0}\left( {c + \frac{{C_{ac}^2}}{{2{a_0}{\Omega ^2}}} + i{b_2}} \right)} }}{{{a_0}}}.\end{array}\] | (14) |
The second root of equation (8) has no physical significance and is therefore not considered. The growth rate of disturbances at the liquid interface is determined as α = Re(ω1). Consequently, we obtain:
| \[\begin{array}{c}\alpha = - \frac{{{a_1}}}{{{a_0}}} + \frac{1}{{2{a_0}}}\left[ {2(a_1^2 + b_1^2 - {a_0}) - \frac{{C_{ac}^2}}{{{\Omega ^2}}} + } \right.\\ + {\left. {2\sqrt {{{\left( {a_1^2 + b_1^2 - {a_0}c - \frac{{C_{ac}^2}}{{2{\Omega ^2}}}} \right)}^2} + {{(2{a_1}{b_1} - {b_2}{a_0})}^2}} } \right]^{1/2}}.\end{array}\] | (15) |
The data for calculations using equation (9) are presented in the Table.
Characteristics of the materials and parameters of external influence
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Research results and discussion
Air-water system
In Fig. 2, a, the dependencies of the growth rate of disturbances at the air – water interface on the wavenumber in the absence of an acoustic field under the influence of electric fields are shown. The velocity difference between the horizontal layers was 15 m/s. This function has only one maximum, regardless of the presence of an electric field (curves 1 – 3). A tangential electric field (β = 0) with a strength of approximately 3·106 V/m stabilizes the Kelvin–Helmholtz instability, which is expressed in a decrease in αm and a shift of the maximum mode km toward lower values (curve 2). A normal electric field (β = π/2) of the same strength, on the contrary, enhances this instability (curve 3), which is consistent with widely accepted concepts [8; 19]. At inclination angles of the electric field vector β π/6, π/4, π/3 (Fig. 2, b), an increase in km is observed from 59,170 m–1 (λm = 106.19 μm) at β = π/6 to 119,709 m–1 (λm = 52.48 μm) at β = π/3. The analysis of neutral curves (Fig. 2, c) showed that the presence of a vertical component of the electric field significantly narrows the range of relative velocity differences between the fluids, within which capillary forces and the tangential electric field suppress the Kelvin–Helmholtz instability. It should be noted that a similar effect was observed in [8] for the case of inviscid dielectric liquids.
Fig. 2. Dependences of growth rate of perturbations of the air–water interface (a, b) |
Let us consider the combined influence of weak acoustic and inclined electric fields on the Kelvin–Helmholtz instability. Fig. 3, a shows the dependencies of the disturbance growth rate at an amplitude value of the acoustic oscillation velocity Ua = 5 m/s. These dependencies indicate that acoustic vibrations suppress the Kelvin–Helmholtz instability (curves 1 – 3), with the tangential electric field amplifying this effect (curve 2), while the normal electric field, on the contrary, weakens it. A weakening of the suppression effect is also observed at electric field inclination angles β π/6, π/4, π/3 (Fig. 3, b), which is confirmed by the analysis of neutral curves (Fig. 3, c). Notably, similar suppression phenomena of the Kelvin–Helmholtz instability were identified in [14]. However, in that study, the application of acoustic fields resulted in a rightward shift of km , while the maximum growth rate increased, indicating an enhancement of the Kelvin–Helmholtz instability. The discrepancy between the results of [14] and the present study may be explained by the fact that in [14], the ratio \(\frac{{C_{ac}^2}}{{2{a_0}{\Omega ^2}}}\) in equation (8) was taken with a negative sign, whereas in this study, it was taken with a positive sign.
Fig. 3. Dependences of the growth rate of disturbances of the air – water interface (a, b) |
Argon-iron system
Now, let us consider a different situation that arises in surfacing or welding processes. In these processes, when the electrode melts in an argon shielding gas environment, a jet of liquid metal forms, which, under certain conditions, breaks up into droplets [20]. The mode of material transfer determines the quality of the formed coating, making the development of methods for controlling this process an important task. In this system, the mutual flow of gas and liquid gives rise to the Kelvin–Helmholtz instability [20]. Fig. 4, a presents dispersion curves, showing that they exhibit two maxima. According to [13], the first maximum is hydrodynamic, while the second is viscosity-induced (curve 1).
Fig. 4. Dependences of the growth rate of disturbances of the argon – iron interface (a – c) |
The application of a tangential electric field with a strength of 3·107 V/m leads to the near-complete suppression of the hydrodynamic maximum (curve 2), whereas in a normal electric field, this effect is weaker (curve 3). As results of [19] show, the change in the sign of the influence of the transverse electric field on capillary instability is associated with the ratio of the specific electrical conductivities σ = σ2 /σ1 and the dielectric permittivities of the fluids ε = ε2 /ε1 . If ε > σ, the electric field has a stabilizing effect; otherwise, when (ε < σ) the electric field has a destabilizing effect [19]. In the case under consideration (see Table), for the argon–iron system σ ~ 0.00133, and ε ~ 0.0002, which should indicate a destabilizing effect of the normal field. However, this is not observed (Fig. 4, a). This discrepancy with capillary instability can be explained by the fact that, in this case, the relative velocity of the flowing layers becomes significant, altering the condition for the occurrence of Kelvin–Helmholtz instability maxima [21]. A further increase in the specific electrical conductivity ratio σ beyond 0.012 leads to the restoration of the hydrodynamic maximum and the complete suppression of the viscosity-induced maximum. When σ ≥ 0.015, the effect changes from stabilizing to destabilizing (Fig. 4, b). The results of studying the effect of inclined electric fields (Fig. 4, c) showed that these fields enhance the Kelvin–Helmholtz instability regardless of the values of σ and ε. In this case, the maximum growth rate is viscosity-induced. At field strengths E20x < 3·107 V/m, a weakly pronounced hydrodynamic maximum is observed. The neutral stability curves indicate that, as in the air – water system, a reduction in the stability region of interface disturbances is observed (Fig. 4, d).
The combined effect of acoustic vibrations with a velocity amplitude of 10 m/s and an electric field with a strength of 3·107 /V/m at σ ~ 0.00133, and ε ~ 0.0002, on the contrary, leads to the complete suppression of the viscosity-induced instability maximum (Fig. 5, a, curve 1) and a sharp reduction in the maximum growth rate αm of disturbances of hydrodynamic origin. The application of a horizontal electric field significantly weakens this effect (Fig. 5, a, curve 2), while in a vertical field, this effect, on the contrary, is amplified (Fig. 5, a, curve 3), despite the fact that at E20x = 0 and E20z = 3·107 V/m, the value of km is greater than E20x = 3·107 V/m and E20z = 0. A change in the sign of the effect to destabilizing also occurs at σ ≥ 0.015 (Fig. 5, b). The application of an inclined electric field, as in the absence of sound, enhances the Kelvin–Helmholtz instability, but αm is somewhat lower (Fig. 5, c). The neutral curves (Fig. 5, d) show an increase in the range of fluid velocities in which capillary forces and tangential fields suppress the Kelvin–Helmholtz instability under the influence of an acoustic field.
Fig. 5. Dependences of the growth rate of disturbances of the argon – iron interface (а – c) |
Conclusions
It has been established that the combined application of inclined electric fields and acoustic vibrations in the air – water system allows the formation of liquid droplets in the range of 10 to 100 μm, even at low gas flow velocities. This opens up new prospects for the development of accelerated cooling technologies for rolled products to achieve high hardness and impact toughness.
Установлено, что совместное применение наклонных электрических полей и акустических колебаний в системе воздух – вода позволяет получать капли жидкости в диапазоне от 10 до 100 мкм даже при малых скоростях движения газа. Это открывает новые перспективы для разработки технологий ускоренного охлаждения проката, для достижения его высокой твердости и ударной вязкости.
For the argon–iron system, it has been shown that a vertical electric field at σ ~ 10–3 and ε ~ 10–4 practically suppresses the hydrodynamic maximum. An increase in the specific electrical conductivity ratio σ beyond 0.012, on the contrary, leads to the restoration of the hydrodynamic maximum and the complete suppression of the viscosity-induced one. At σ ≥ 0.015, the effect changes from stabilizing to destabilizing, regardless of the number of maxima in the dependence of the growth rate on the wavelength. The application of a tangential electric field completely suppresses the Kelvin–Helmholtz instability.
The combined effect of acoustic vibrations and a normal electric field leads to the complete suppression of the viscosity-induced instability maximum and a sharp reduction in the maximum growth rate of disturbances of hydrodynamic origin, while in a horizontal electric field, this effect is significantly weaker.
References
1. Praturi D.S., Girimaji S.S. Mechanisms of canonical Kelvin-Helmholtz instability suppression in magnetohydrodynamic flows. Physics of Fluids. 2019;31(2):024108. https://doi.org/10.1063/1.5083857
2. Rahmani M., Seymour B.R., Lawrence G.A. The effect of Prandtl number on mixing in low Reynolds number Kelvin-Helmholtz billows. Physics of Fluids. 2016;28(5):054107. https://doi.org/10.1063/1.4949267
3. Panin V.E., Gromov V.E., Romanov D.A., Budovskikh E.A., Panin S.V. The physical basics of structure formation in electroexplosive coatings. Doklady Physics. 2017;62:67‒70. https://doi.org/10.1134/S1028335817020112
4. Mishin V.V., Tomozov V.M. Kelvin–Helmholtz instability in the solar atmosphere, solar wind and geomagnetosphere. Solar Physics. 2016;291:3165‒3184. https://doi.org/10.1007/s11207-016-0891-4
5. Petrarolo A., Kobald M., Schlechtriem S. Understanding Kelvin–Helmholtz instability in paraffin-based hybrid rocket fuels. Experiments in Fluids. 2018;59:62. https://doi.org/10.1007/s00348-018-2516-1
6. Grigor’ev A.I., Shiryaev A.A., Shiryaeva S.O. Instability of a charged droplet in an inhomogeneous electrostatic field of a rod of finite thickness. Fluid Dynamics. 2018;53(1):34–48. https://doi.org/10.1134/S0015462818010081
7. Saraev Yu.N., Chinakhov D.A., Ilyashchenko D.I., Kiselev A.S., Gordynets A.S. Investigation of the stability of melting and electrode metal transfer in consumable electrode arc welding using power sources with different dynamic characteristics. Welding International. 2017;31(10):784–790. https://doi.org/10.1080/09507116.2017.1343977
8. Korovin V.M. Effect of tilted electrostatic field on the Kelvin–Helmholtz instability in a liquid dielectric and gas flow. Technical Physics. 2017;62:1316‒321. https://doi.org/10.1134/S1063784217090134
9. Sarychev V.D., Khaimzon B.B., Nevskii S.A., Il’yashchenko A.V., Grishunin V.A. Mathematical models of mechanisms for rolled products accelerated cooling. Izvestiya. Ferrous Metallurgy. 2018;61(4):326–332. (In Russ.). https://doi.org/10.17073/0368-0797-2018-4-326-332
10. Awasthi M.K., Asthana R., Agrawal G.S. Viscous correction for the viscous potential flow analysis of Kelvin–Helmholtz instability of cylindrical flow with heat and mass transfer. International Journal of Heat and Mass Trans. 2014;78:251‒259. https://doi.org/10.1016/j.ijheatmasstransfer.2014.06.082
11. Barreras F., Lozano A., Dopazo C. Linear instability analysis of the viscous longitudinal perturbation on an air-blasted liquid sheet. Atomization and Sprays. 2001;11(2):139‒154. https://doi.org/10.1615/ATOMIZSPR.V11.I2.30
12. Logvinov O.A. Linear stability of stratified flow of two viscous fluids. Moscow University Mechanics Bulletin. 2022;77; 117–126. https://doi.org/10.3103/S0027133022040021
13. Sarychev V.D., Granovskii A.Yu., Gromov V.E. Model of formation of inner nanolayers in shear flows of material. Technical Physics. 2013;58(10):1544‒157. https://doi.org/10.1134/S1063784213100113
14. Bychkov V. Analytical scalings for flame interaction with sound waves. Physics of Fluids. 1999;11(10):3168‒3173. https://doi.org/10.1063/1.870173
15. Bilgili S., Ugarte O., Akkerman V. Interplay of Kelvin–Helmholtz instability with acoustics in a viscous potential flow. Physics of Fluids. 2020;32(8):084108. https://doi.org/10.1063/5.0017448
16. Awasthi M.K., Dutt N., Kumar A., Kumar S. Electrohydrodynamic capillary instability of Rivlin–Ericksen viscoelastic fluid film with mass and heat transfer. Heat Transfer. 2024;53(1):115–133. https://doi.org/10.1002/htj.22944
17. Saville D.A. Electrohydrodynamic stability: effects of charge relaxation at the interface of a liquid jet. Journal of Fluid Mechanics. 1971;48(4):815–827. https://doi.org/10.1017/S0022112071001873
18. Shkadov V.Ya., Shutov A.A. Stability of a surface-charged viscous jet in an electric field. Fluid Dynamics. 1998;33(2):176–185. https://doi.org/10.1007/BF02698699
19. Awasthi M.K. Study on electrohydrodynamic capillary instability of viscoelastic fluids with radial electric field. International Journal of Applied Mechanics. 2014;6(4):1450037. https://doi.org/10.1142/S1758825114500379
20. Zhao Y., Chung H. Numerical simulation of droplet transfer behavior in variable polarity gas metal arc welding. International Journal of Heat and Mass Transfer. 2017;111:1129‒1141. https://doi.org/10.1016/j.ijheatmasstransfer.2017.04.090
21. Nevskii S.A., Sarychev V.D., Granovsky A.Yu., Bashchenko L.P., Gromov V.E. Formation of micro- and nano- in electroexplosive carboborization of titanium alloys by the mechanism hydrodynamic instabilities. Fundamental’nye problemy sovremennogo materialovedenia (Basic Problems of Material Science (BPMS)). 2023;20(3):317–328. (In Russ.). https://doi.org/10.25712/ASTU.1811-1416.2023.03.004
About the Authors
S. A. NevskiiRussian Federation
Sergei A. Nevskii, Dr. Sci. (Eng.), Assist. Prof. of the Chair of Science named after V.M. Finkel’
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
L. P. Bashchenko
Russian Federation
Lyudmila P. Bashchenko, Cand. Sci. (Eng.), Assist. Prof. of the Chair “Thermal Power and Ecology”
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
V. D. Sarychev
Russian Federation
Vladimir D. Sarychev, Cand. Sci. (Eng.), Assist. Prof. of the Chair of Sciences named after V.M. Finkel’
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
A. Yu. Granovskii
Russian Federation
Aleksei Yu. Granovskii, Cand. Sci. (Eng.), Senior Researcher of the Department of Scientific Research
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
D. V. Shamsutdinova
Russian Federation
Diana V. Shamsutdinova, Student of Institute of Pedagogical Education
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
Review
For citations:
Nevskii S.A., Bashchenko L.P., Sarychev V.D., Granovskii A.Yu., Shamsutdinova D.V. Influence of inclined electric field on decay of a liquid jet during heat treatment and surfacing. Izvestiya. Ferrous Metallurgy. 2025;68(1):30-39. https://doi.org/10.17073/0368-0797-2025-1-30-39