Functional properties of plastic deformation resistance of 12Kh18N10T steel

Introduction

The most productive and efficient method for manufacturing long metal products is continuous rolling. Recently, this method has been widely used in the production of rolled sections, strips, and pipes [1 – 3]. On the other hand, the quality of the final product rolled on continuous mills is significantly influenced by the adjustment of the mill’s rate mode, which, in turn, determines the level of energy-power parameters. Therefore, to establish an optimal rate mode for the continuous rolling process, it is necessary to have relationships that link the kinematic parameters with the forces acting on the deformation zone boundaries.

Several studies [4 – 6] describe a methodology for determining such relationships. Analysis of the results obtained using this methodology for calculating rolling forces in continuous rolling has shown that the calculated values correspond quite well to actual values but are consistently underestimated. It should be noted that the rolling force is directly proportional to the metal’s resistance to plastic deformation [7]. Further research has revealed that commonly used methods for calculating the resistance of metals to plastic deformation [8; 9] provide underestimated results when calculating the technological parameters of continuous rolling processes. This discrepancy arises because these methods do not account for the actual transformation of strength properties, particularly the residual strengthening after rolling in the previous stand of the mill. The effect of deformation history on the resistance of metals to plastic deformation during continuous hot strip rolling is also noted in [10]; however, the modeling employs expressions similar to those mentioned earlier. The above observations highlight the need for additional research into the resistance to plastic deformation of various steel grades.

One of the most in-demand types of metal products is seamless pipes made from stainless steel grades, particularly 12Kh18N10T [11]. Since continuous rolling is the most productive and economically efficient process for shell rolling in the production of seamless pipes [12; 13], studying the patterns of plastic deformation resistance formation in 12Kh18N10T steel during continuous rolling is highly relevant.

Research methods

In this study, experiments were conducted using the modern universal testing system Gleeble 3800 [14 – 16] in a vacuum environment (low vacuum) on the PocketJaw module, with chromel-alumel thermocouples welded to the samples (for temperature control during heating and measurement of deformation-induced heating). The samples were heated at a rate of 5 °C/s to the test temperature, followed by a 5-min hold, using electric current. High-temperature sensors for longitudinal and transverse deformation were used to measure deformation.

To determine the strain hardening rate of the steel, tensile tests were conducted at room temperature. The working hypothesis assumed that softening processes were absent under these conditions.

The behavior of metal resistance to plastic deformation during testing depends on its initial value, which, in turn, is influenced by the heating temperature. Therefore, a separate series of tensile tests was conducted on 12Kh18N10T steel samples at temperatures ranging from 800 to 1200 °C in 100 °C increments.

To determine the softening rate, stepwise tensile testing of cylindrical samples was performed with varying pause durations at temperatures from 800 to 1200 °C in 100 °C increments. It was assumed that during the pauses, no hardening processes occurred, and the decrease in stress characterized the softening rate.

All experimental data were processed using the least squares method in accordance with the methodology presented in [17].

Results

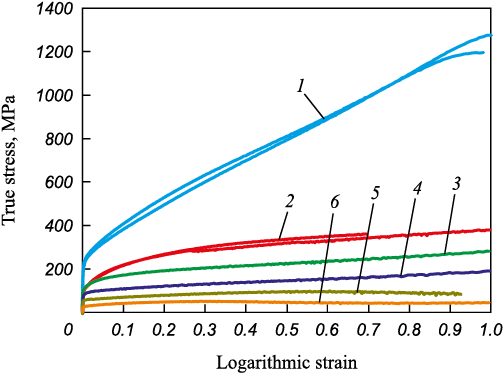
The general appearance of the strain hardening curves for 12Kh18N10T stainless steel, obtained from uniaxial tensile tests at various temperatures, is shown in Fig. 1.

The approximation of the strain hardening curve was based on results obtained at a temperature of 25 °C (Table 1).

In [18], it is noted that a power-law relationship is well-suited for approximating the dependence of the plastic deformation resistance of metals and alloys on strain level in cold conditions. Processing the experimental data using the least squares method yielded the following equation for 12Kh18N10T steel

σ_s0 = 200 + 1064ε^0.78,

where ε is the logarithmic strain.

The statistical processing of experimental data (Table 2) also made it possible to determine the nature of the temperature’s influence on the initial resistance of 12Kh18N10T steel to plastic deformation.

The resulting empirical relationship can be represented as

\[{\sigma _{s0}}({\theta _0}) = 200{\left( {\frac{{1350 - {\theta _0}}}{{1325}}} \right)^{0,87}},\]

where θ₀ is the heating temperature of the sample.

It should be noted that the plastic deformation resistance of 12Kh18N10T steel in tensile tests has been previously studied. For example, in [19], based on extensive experimental research, an original methodology was proposed. According to this methodology, regardless of the steel grade, the ratio of the actual value of the metal’s plastic deformation resistance σ_s to the average σ_sс for a given strain ε remains constant. The average plastic deformation resistance value is determined experimentally. Specifically, at South Ural State University, using this methodology and a cam plastometer, the following relationship was obtained for 12Kh18N10T steel:

σ_sс = 1892u^0.0974ε^0.2637exp(–0.0022t),

where u is the strain rate; t is the heating temperature.

At the same time, it should be noted that the reliability of the results obtained thus far requires verification, as the equipment, methodologies, and measurement techniques used had certain errors.

On the other hand, the capabilities of modern research equipment significantly enhance the accuracy of results and broaden their applicability. In particular, stepwise loading of samples now enables the study of softening behavior during inter-deformation pauses. Similar studies using the Gleeble 3800 universal testing system are known [20], although they primarily focus on examining the metal structure. Therefore, stepwise tensile tests were conducted to obtain the relationship of the softening coefficient [8] as a function of temperature. As an example, Fig. 2 shows a record of the changes in the metal’s plastic deformation resistance, taking into account the inter-deformation pause.

As a result, processing the presented experimental data using the least squares method yielded the following relationship:

\[k = 4.75\frac{{1350 - t}}{{t - 25}} - 0.93.\]

Analysis and discussion of results

The investigation of the plastic deformation resistance of 12Kh18N10T steel confirmed the existing information regarding the intensive strain hardening of this steel grade during cold deformation. The hardening behavior is accurately described by a power-law relationship.

The proposed new relationship for the initial plastic deformation resistance of 12Kh18N10T steel as a function of heating temperature provides a satisfactory qualitative and quantitative description of this dependence. A relatively large error is observed at a temperature of about 900 °C. However, on the other hand, the shell rolling process occurs at higher temperatures, where the proposed relationship shows good agreement with the actual data. Nevertheless, the search for a more suitable regression equation remains an open question.

The temperature dependence of the softening coefficient for 12Kh18N10T steel was determined for the first time. Previously, no attempts had been made to include a constant term in this equation. An analysis of the proposed relationship revealed that, according to calculations, the softening coefficient may take negative values at higher temperatures. This outcome lacks physical validity, as the softening coefficient represents the time required for the metal to fully soften. To address this issue, the constant term in the formula should be set to zero or higher. However, calculations indicate that this adjustment compromises the accuracy of the approximation at lower temperatures. Therefore, it is suggested to retain the current formula but assign a value of zero to the softening coefficient in cases where negative values are calculated. Alternatively, a more suitable regression equation could be developed to address this issue.

The investigation of the softening behavior of 12Kh18N10T steel at high temperatures revealed a distinct characteristic: it exhibits more intense softening between reductions compared to, for instance, ferritic-pearlitic steels [8].

As previously demonstrated [17], to determine the actual value of metal plastic deformation resistance while accounting for its time-dependent evolution, the entire duration of the deformation process, including pauses between reductions, is divided into discrete time intervals. For each i-th time interval, the plastic deformation resistance is calculated using a recursive formula.

The results of the study on the plastic deformation resistance of 12Kh18N10T steel allow for the proposal of the following recursive equation for determining this resistance within the temperature range of 900 – 1200 °C

\[\begin{array}{c}{\sigma _{si}} = 200{\left( {\frac{{1350 - {\theta _0}}}{{1325}}} \right)^{0.87}} + \\ + \sum\limits_{i = 1}^m {\left\{ {1064\left( {\varepsilon _i^{0.78} - \varepsilon _{i - 1}^{0.78}} \right) + \left( {{\sigma _{s(i - 1)}} - {\sigma _0}} \right) \times } \right.} \\ \times \left. {\left[ {\exp \left( { - \frac{{\Delta {\tau _i}}}{{4.75\frac{{1350 - t}}{{t - 25}}}}} \right) - 1} \right]} \right\},\end{array}\]

where i is the number of the time interval into which the deformation time is divided; m is the total number of time intervals into which the deformation time is divided; Δτ_i is the duration of the time interval.

Conclusions

The plastic deformation resistance of 12Kh18N10T steel in the hot state was studied. In addition to determining specific empirical coefficients, a notable characteristic of stainless steel deformation was identified – a significantly higher softening rate compared to ferritic-pearlitic steels.

The extensive experimental data collected can be used to calculate the deformation parameters and energy-power characteristics of the continuous shell rolling process for austenitic stainless steels on mills equipped with a controlled moving mandrel.