Функциональные свойства сопротивления пластической деформации стали 12Х18Н10Т

Введение

Наиболее производительным и эффективным способом получения длинномерных металлических изделий является непрерывная прокатка. В последнее время ее широко используют при производстве сортового металла, полос и труб [1 – 3]. С другой стороны, на качество готового продукта, прокатываемого на непрерывных станах, существенное влияние оказывает настройка скоростного режима стана, которая, в свою очередь, определяет уровень энергосиловых параметров. Поэтому для определения рационального скоростного режима процесса непрерывной прокатки необходимо иметь зависимости, связывающие кинематические параметры с усилиями, действующими на границах очага деформации.

Известен ряд работ [4 – 6], в которых описана методика определения такой взаимосвязи. Анализ получаемых с ее помощью результатов расчета усилия при непрерывной прокатке показал, что они достаточно хорошо совпадают с реальными значениями, однако всегда являются заниженными. При этом следует отметить, что усилие прокатки прямо пропорционально сопротивлению металла пластической деформации [7]. Согласно дальнейшим исследованиям было выявлено, что обычно используемые методики расчета сопротивления металла пластической деформации [8; 9] дают заниженные результаты при расчетах технологических параметров процессов непрерывной прокатки, так как не учитывают реальную трансформацию прочностных свойств, в частности остаточное упрочнение после прокатки в предыдущей клети стана. Влияние истории деформирования на величину сопротивления металла пластической деформации при непрерывной горячей прокатке полос также отмечается в работе [10], однако для моделирования используются выражения, аналогичные упомянутым выше. Отмеченное выше свидетельствует о необходимости проведения дополнительных исследований сопротивления пластической деформации различных марок стали.

Одним из востребованных видов металлопродукции являются бесшовные трубы из нержавеющих марок стали, в частности марки 12Х18Н10Т [11]. Поскольку непрерывная прокатка – это наиболее производительный и экономически выгодный процесс раскатки гильз при производстве бесшовных труб [12; 13], актуальным является исследование закономерностей формирования сопротивления пластической деформации стали 12Х18Н10Т именно при непрерывной прокатке.

Методы исследования

В настоящей работе эксперименты проводились с использованием современной универсальной испытательной установки Gleeble 3800 [14 – 16] в вакуумной среде (низкий вакуум) на модуле PocketJaw с приваркой к образцам хромель-алюмелевых термопар (для контроля температуры при нагреве, а также измерения деформационного разогрева). Нагрев образцов со скоростью 5 °C/с до температуры испытания с последующей 5-мин выдержкой осуществлялся пропусканием электрического тока. Для измерения деформации использованы высокотемпературные датчики продольной и поперечной деформации.

С целью определения скорости деформационного упрочнения стали проведены опыты на растяжение при комнатной температуре. В качестве рабочей гипотезы принималось, что в этом случае процессы разупрочнения отсутствуют.

Характер изменения сопротивления металла пластической деформации в процессе испытаний зависит от значения этой величины в исходном состоянии, которая, в свою очередь, зависит от температуры нагрева. В связи с этим проведена отдельная серия испытаний по растяжению образцов из стали 12Х18Н10Т при температурах от 800 до 1200 °C с шагом 100 °C.

Чтобы определить скорость процессов разупрочнения, проводилось ступенчатое растяжение цилиндрических образцов с различным временем паузы при температурах от 800 до 1200 °C с шагом 100 °C. При этом считалось, что во время паузы процессы упрочнения отсутствуют и падение напряжения характеризует скорость разупрочнения.

Все полученные экспериментальные данные обрабатывались с помощью метода наименьших квадратов в соответствии с методикой, представленной в работе [17].

Полученные результаты

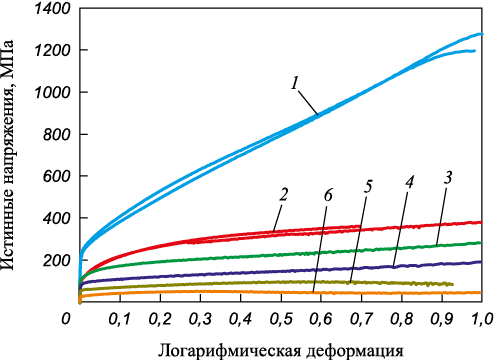
Общий вид кривых упрочнения нержавеющей стали 12Х18Н10Т, полученных в опытах на одноосное растяжение при различных температурах, приведен на рис. 1.

Для аппроксимации кривой деформационного упрочнения использовались результаты, полученные при температуре 25 °С (табл. 1).

В работе [18] отмечено, что для аппроксимации зависимости сопротивления пластической деформации металлов и сплавов от степени деформации в холодном состоянии достаточно хорошо подходит степенная зависимость. Обработка экспериментальных данных с помощью метода наименьших квадратов позволила получить для стали 12Х18Н10Т уравнение

σ_s0 = 200 + 1064ε^0,78,

где ε – логарифмическая деформация.

Статистическая обработка экспериментальных данных (табл. 2) дала возможность также определить характер влияния температуры на начальное сопротивление стали 12Х18Н10Т пластической деформации.

Полученная при этом эмпирическая зависимость может быть представлена в виде

\[{\sigma _{s0}}({\theta _0}) = 200{\left( {\frac{{1350 - {\theta _0}}}{{1325}}} \right)^{0,87}},\]

где θ₀ – температура нагрева заготовки.

Следует отметить, что сопротивление пластической деформации стали 12Х18Н10Т в опытах на растяжение исследовалось и ранее. Так, например, в работе [19] на основе многочисленных экспериментальных исследований предложена оригинальная методика, согласно которой вне зависимости от марки стали отношение фактического значения сопротивления металла пластической деформации σ_s к среднему σ_sс для определенной степени деформации ε остается постоянным. При этом среднее значение сопротивления металла пластической деформации определяется экспериментально. В частности, в Южно-Уральском государственном университете с использованием этой методики и кулачкового пластометра для стали 12Х18Н10Т получена следующая зависимость:

σ_sс = 1892u^0,0974ε^0,2637exp(–0,0022t),

где u – скорость деформации; t – температура нагрева.

В тоже время следует отметить, что достоверность полученных в настоящее время результатов требует проверки, поскольку применяемые оборудование, методики и способы измерений имели определенную погрешность.

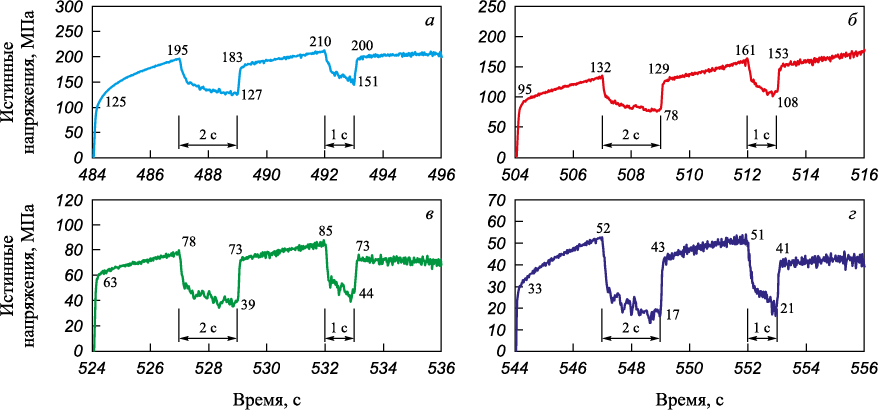
С другой стороны, возможности современного исследовательского оборудования позволяют существенно повысить достоверность результатов и расширить диапазон их применения. В частности, появляется возможность ступенчатого нагружения образцов и исследования таким образом закономерностей разупрочнения во время междеформационной паузы. Известно проведение подобных исследований с помощью универсальной испытательной установки Gleeble 3800 [20], однако они в большей степени ориентированы на изучение структуры металла. Поэтому были проведены опыты на ступенчатое растяжение образцов для получения зависимости коэффициента разупрочнения [8] от температуры. В качестве примера на рис. 2 приведена запись изменения сопротивления металла пластической деформации с учетом междеформационной паузы.

В результате обработка представленных экспериментальных данных с помощью метода наименьших квадратов позволила получить следующую зависимость:

\[k = 4,75\frac{{1350 - t}}{{t - 25}} - 0,93.\]

Анализ и обсуждение полученных результатов

Исследование сопротивления пластической деформации стали 12Х18Н10Т подтвердило имеющуюся в настоящее время информацию об интенсивном упрочнении этой марки стали при холодной деформации. При этом характер упрочнения достаточно точно описывается степенной зависимостью.

Предложенный новый вид зависимости исходного уровня сопротивления пластической деформации стали 12Х18Н10Т от температуры нагрева качественно правильно и количественно удовлетворительно описывает эту зависимость. Достаточно большая погрешность имеет место при температуре порядка 900 °С. Однако, с другой стороны, процесс раскатки гильзы происходит при более высоких температурах, при которых полученная зависимость имеет достаточно хорошую сходимость с фактическими данными. Тем не менее вопрос поиска более подходящей формы уравнения регрессии остается.

Зависимость коэффициента разупрочнения стали 12Х18Н10Т от температуры получена впервые. При этом ранее не было прецедентов использования в этом уравнении свободного члена. Анализ предложенной новой зависимости показал, что в результате расчета по ней при больших температурах коэффициент разупрочнения может принимать отрицательные значения, что лишено физического смысла, так как коэффициент разупрочнения представляет собой промежуток времени, за который металл полностью разупрочняется. Поэтому, чтобы в формуле вышеуказанное гарантированно учитывалось, свободный член следует принять как минимум равным нулю. Однако, как показали расчеты, при этом ухудшается качество аппроксимации при более низких температурах. Таким образом, предлагается оставить вид формулы неизменным, но в случае получения отрицательных значений коэффициента разупрочнения принимать его равным нулю. Альтернативный вариант связан с поиском нового, более подходящего вида уравнения регрессии.

Исследование характера разупрочнения стали 12Х18Н10Т при высоких температурах позволило выявить еще одну ее особенность, а именно более интенсивный характер ее разупрочнения в промежутках между обжатиями по сравнению, например, со сталями феррито-перлитного класса [8].

Ранее было показано [17], что для определения актуальной величины сопротивления металла пластической деформации с учетом ее развития во времени, весь временной отрезок процесса деформирования, включая паузы между обжатиями, разбивается на временные промежутки и для каждого i-го временного промежутка сопротивление пластической деформации вычисляется по рекуррентной формуле.

Результаты исследования сопротивления пластической деформации стали 12Х18Н10Т позволяют предложить для его определения в диапазоне температур 900 – 1200 °С следующее рекуррентное уравнение

\[\begin{array}{c}{\sigma _{si}} = 200{\left( {\frac{{1350 - {\theta _0}}}{{1325}}} \right)^{0,87}} + \\ + \sum\limits_{i = 1}^m {\left\{ {1064\left( {\varepsilon _i^{0,78} - \varepsilon _{i - 1}^{0,78}} \right) + \left( {{\sigma _{s(i - 1)}} - {\sigma _0}} \right) \times } \right.} \\ \times \left. {\left[ {\exp \left( { - \frac{{\Delta {\tau _i}}}{{4,75\frac{{1350 - t}}{{t - 25}}}}} \right) - 1} \right]} \right\},\end{array}\]

где i – номер временных интервалов, на которые разбивается промежуток времени деформирования; m – число временных интервалов, на которые разбивается промежуток времени деформирования; Δτ_i – продолжительность временного интервала.

Выводы

Изучено сопротивление пластической деформации стали 12Х18Н10Т в горячем состоянии. При этом, наряду с определением конкретных значений эмпирических коэффициентов, обнаружена еще одна особенность деформирования нержавеющих марок стали – гораздо более высокие скорости разупрочнения, чем у сталей феррито-перлитного класса.

Полученный комплекс экспериментальной информации может быть использован при определении формоизменения и энергосиловых параметров процесса непрерывной раскатки гильз из нержавеющих марок стали аустенитного класса на непрерывных раскатных станах с контролируемо-перемещаемой оправкой.