Перейти к:
Вид обобщенной математической модели для описания больших горячих деформаций
https://doi.org/10.17073/0368-0797-2024-5-616-624
Аннотация
Взаимосвязь температурно-деформационно-силовых параметров в процессах горячей деформации имеет важное значение в практике обработки давлением. Из двух вариантов поиска и описания таких связей (основанных на физических закономерностях и математических приемах) в некоторых случаях оказывается более простым способ математического поиска искомой зависимости. Именно такой путь реализован в данной работе. Для этого из оцифрованных диаграмм деформации образцов жаропрочной 12 %-ной хромистой стали 1Cr12Ni3Mo2VNbN, продеформированных до истинной степени деформации ~1 при 1253 – 1453 К и скорости сжатия 0,01 – 10 с–1 в истинных координатах (φ и S) создавали матрицу исходных данных, в которой для каждой точки экспериментальной диаграммы деформации указывались напряжение S, степень деформации φ, скорость деформации φ′ и температура Т. Проведен поиск математической модели в мультипликативной форме, что позволило логарифмированием привести ее к линейному виду, а для поиска коэффициентов при сомножителях (а после логарифмирования – при слагаемых) использовать стандартные операторы программы Mathcad, использующие алгоритмы расчетов на основе метода наименьших квадратов. Качество модели оценивали количественно через расчет Q – суммы квадратов разностей между расчетными и экспериментальными значениями напряжений с нормировкой ее на среднее значение напряжения S от всего массива. Для найденной наилучшей формы связи S = f(φ, φ′, T) вида \(\log (S) = A + B\log (\varphi ) + C{[\log (\varphi )]^2} + D{[\log (\varphi )]^3} + E\log (\varphi ') + F\log (\varphi )\log (\varphi ') + G\frac{\varphi }{{\varphi '}} + \frac{{H + K\varphi + M\log (\varphi ) + N\log (\varphi ') + P\log (\varphi )\log (\varphi ')}}{T}\) значение Q составило 6 % от Sср = 130 МПа. Установлено, что найденный вид математического описания горячей деформации применим к анализу процессов горячей деформации самых разнообразных металлических материалов, при этом точность прогнозных характеристик напряжения деформирования составляет 3 – 11 %.
Ключевые слова
Для цитирования:
Беломытцев М.Ю. Вид обобщенной математической модели для описания больших горячих деформаций. Известия высших учебных заведений. Черная Металлургия. 2024;67(5):616-624. https://doi.org/10.17073/0368-0797-2024-5-616-624
For citation:
Belomyttsev M.Yu. Type of generalized mathematical model for describing large hot deformations. Izvestiya. Ferrous Metallurgy. 2024;67(5):616-624. https://doi.org/10.17073/0368-0797-2024-5-616-624
Введение
Обработка давлением является главным способом получения металлопродукции заданного сортамента и типоразмера. С точки зрения эффективности производства (баланса затрат на оборудование и нагрев заготовок) бесспорным преимуществом обладает обработка горячей деформацией. Холодная деформация применяется для придания высоких механических свойств на финишной стадии обработки давлением с помощью механизма холодного наклепа (лист, проволока, лента, пруток и т. п.).
Возможности управления процессами горячей деформации определяются знаниями законов связи таких переменных факторов, как давление, деформация, скорость деформации и температура. Знание этих закономерностей позволяет вводить компьютерное регулирование процессами горячей деформации (по типу «контролируемой прокатки» для автолистовой стали) с целью регулирования структуры и механических свойств конечного продукта.
Известны базовые уравнения связи переменных типа Холломона (Н) [1; 2], экспоненциально-степенного (ES) [3], Людвигсона (L) [4], Зенера-Холломона (Z и Z1) [5; 6], Bird–Mukherjee–Dorn (BMD) [7], модернизированное уравнение Зенера-Холломона (ZM) [5], Джонсона-Кука (DK) [8]. Эти уравнения математически выглядят следующим образом:
| S = S0 φ\(^n\); | (H) |
| σ = Aε\(^n\)exp(kε); | (ES) |
| S = K0 φ\(^n\) + exp(K1 + K2φ); | (L) |
| \[\sigma = \left( {A + B{\varepsilon ^n}} \right)\left[ {1 + C\ln \left( {\frac{{\varepsilon '}}{{{{\varepsilon '}_0}}}} \right)} \right]{\left( {1 - \frac{{T - {T_r}}}{{{T_m} - {T_r}}}} \right)^m};\] | (DK) |
| \[Z = \dot \varepsilon \exp \left( {\frac{Q}{{RT}}} \right);\] | (Z) |
| \[\dot \varepsilon = AF(\sigma )\exp \left( { - \frac{Q}{{RT}}} \right),\] | (Z1) |
где S – истинное напряжение, МПа; S0 , K0 , K1 , K2 , A, α, n – константы материала, α = β/n; φ – истинная деформация, доли ед.; σ – напряжения течения, МПa; ε – деформация, доли ед.; Z – параметр Зенера-Холломона; \(\dot \varepsilon \) – скорость деформации, с\(^–\)1; Q – энергия активации горячей деформации, кДж/моль; R – универсальная газовая постоянная, 8,314 Дж/моль·К; Т – абсолютная температура, К; F(σ) = σ\(^θ\), ασ < 0,8; F(σ) = exp(βσ), ασ > 1,2; F(σ) = [sin h (ασ)]\(^n\) для всех остальных ασ.
Замена гиперболическим законом F(σ) в уравнении (Z1) дает
| \[\dot \varepsilon = A{[\sin h(\alpha \sigma )]^n}\exp \left( { - p\frac{Q}{{RT}}} \right),\] | (А) |
где р – константа.
Уравнение (A) – уравнение Аррениуса в форме гиперболического синуса [9; 10] может лучше описывать зависимость напряжения от температуры и скорости деформации на стадии установившегося течения. Согласно определению гиперболического закона, напряжение течения может быть выражено как функция параметра Зенера-Холломона в виде:
| \[\sigma = \frac{1}{\alpha }\ln \left\{ {{{\left( {\frac{Z}{A}} \right)}^{1/n}} + {{\left[ {{{\left( {\frac{Z}{A}} \right)}^{2/n}} + 1} \right]}^{1/2}}} \right\};\] | (Z) |
| \[\dot \varepsilon = {D_0}EbA\frac{\sigma }{E}\frac{b}{d}\exp \left( { - \frac{Q}{{RT}}} \right)\frac{1}{{kT}};\] | (BMD) |
| \[\sigma = \frac{{{\beta _0}}}{\alpha }{\varepsilon ^{{\beta _1}}}\exp ( - {\beta _2}\varepsilon )\ln \left[ {{{\left( {\frac{Z}{A}} \right)}^{1/n}} + {{\left( {\frac{Z}{A} + 1} \right)}^{1/2}}} \right].\] | (ZM) |
Описанные выше уравнения не универсальны. Уравнение типа Холломона (H) применяют для нахождения параметров кривой холодной и теплой деформации, когда до самого момента потери устойчивости пластического течения (чаще всего, до момента образования шейки) на машинной кривой деформации коэффициент деформационного упрочнения dσ/δε положителен (т. е. кривая все время идет вверх, хотя и с постоянно убывающим наклоном). Уравнение (ES) хорошо описывает кривую горячей деформации, на которой присутствует стадия с постоянно уменьшающейся (хотя и довольно медленно) по мере увеличения деформации нагрузкой, не связанной с началом образования шейки (на этой стадии процессы контролируются динамической полигонизацией), но плохо – со стадией динамической рекристаллизации. Первые два типа уравнений не учитывают температуры и скорости деформации. Уравнения Зенера-Холломона (ZM) и его разновидности применяют для описания тех кривых горячей деформации, на которых ярко выражена стадия с постоянной скоростью деформации (на этой стадии кривая идет параллельно оси абсцисс, что может быть связано как с динамической полигонизацией, так и с динамической рекристаллизацией). Найденные уравнения позволяют прогнозировать связь скорости деформации на этой стационарной стадии с температурой и напряжением, но без учета степени деформации.
Количество видов обобщенных (т. е. с учетом всех четырех факторов – деформации ε, ее скорости \(\dot \varepsilon \), температуры Т и напряжения σ) математических зависимостей связи переменных, к которым стремятся свести результаты опытов различные исследователи, невелико. Это зависимости Аррениусовского (общего) вида
\[\sigma = A{\varepsilon ^n}{\dot \varepsilon ^m}\exp \left( {\frac{Q}{{RT}}} \right),\]
зависимость Зерилли-Армстронга вида
σ = C0 + C2 ε\(^{1/2}\) exp[–C3T + C4 ln(\(\dot \varepsilon \))]
и комбинированное уравнение
\[\sigma = A{\varepsilon ^n}{\rm{exp(}}k\varepsilon {\rm{)}}{\dot \varepsilon ^m}\exp \left( {\frac{Q}{{RT}}} \right),\]
где С0 , С2 , С3 , С4 – константы.
Взаимосвязь всех четырех переменных (σ, ε, \(\dot \varepsilon \), Т) может быть представлена уравнениями общего вида (OB) [1; 11]
| \[\sigma = A{\varepsilon ^n}{\dot \varepsilon ^m}\exp \left( {\frac{Q}{{RT}}} \right)\] | (1.1) |
или после логарифмирования
| \[\log (\sigma ) = A + B\log (\varepsilon ) + C\log (\dot \varepsilon ) + \frac{D}{T}.\] | (1.1а) |
Комбинирование уравнений (ES) и (OB) [12] дает
или после логарифмирования
Известно также уравнение общего вида Зерилли-Армстронга [13]
σ = С0 + С2 ε\(^{1/2}\) exp[(–C3 T + C4 ln(\(\dot \varepsilon \))],
после логарифмирования которого (полагая на начальном цикле С0 = 0) связь переменных может быть выражена функциональной зависимостью вида
log(σ) = A + B log(ε) + C log(\(\dot \varepsilon \)) + DT.
Все эти уравнения применяют как для описания процессов деформирования, так и для прогноза (расчета) требуемых инженерами или исследователями параметров – напряжений, деформаций, либо скоростей деформаций.
Некоторые исследователи вводят в модели деформации структурные параметры (размер зерна, плотность дислокаций и т. п.). Таковы наиболее часто используемые разновидности модели Bird–Mukherjee–Dorn (BMD) и Джонсона-Кука (DK) [7; 8]. Однако в случае применения таких методик приходится предварительно определять большое число структурных параметров для каждой кривой деформации (до трех), вследствие чего общее число определяемых переменных может составлять несколько десятков.
Экспериментальную часть исследований по горячей деформации проводят на тестовых образцах малых размеров. Параметры горячей обработки давлением имитируют, изменяя температуру, скорость, степень деформации и фиксируя при этом нагрузку, возникающую в образце. Целью таких испытаний является получение набора кривых деформации, построенных в координатах «деформация ε – напряжение σ» при варьировании температуры испытания Т и условной скорости деформации \(\dot \varepsilon \), которые в единичном опыте поддерживаются постоянными, а далее – в нахождении формулы, связывающей все переменные (как зависимые, так и независимые). Такова процедура построения обобщенной математической модели горячей деформации. Для адекватного сопоставления механического поведения образцов в таких испытаниях с эволюцией структуры опыты проводят по схеме, позволяющей поддерживать в течение всего опыта постоянную истинную скорость деформации φ′, а регистрируемое усилие на образце пересчитывают в истинное напряжение S. При использовании «истинных координат» S и φ учитывается изменение размеров образцов в процессе деформации (при использовании «условных координат» σ и ε все рассчитываемые механические характеристики относят к начальным размерам образцов).
Анализ математических методов, применяемых для получения коэффициентов тех или иных зависимостей, приводит к выводу, что наиболее простыми являются методики «одного шага», позволяющие логарифмированием или иным математическим преобразованием приводить исходную модель (выбранную в качестве проверяемой гипотезы на ее качество) к линейному виду, после чего определение коэффициентов такой модели становится тривиальным (процедура нахождения коэффициентов линейных уравнений в типовых расчетных программах Excel, Mathcad, Origin, Mathlab, Statistica и им подобных предельно проста и формализована). В противовес им процедура нахождения коэффициентов при переменных в законе деформации вида Z1, наиболее часто используемая исследователями, многошаговая, с несколькими промежуточными этапами анализа. Авторами работ [14; 15] на основе упрощения поиска закона деформации была разработана методика для анализа процесса ползучести, в которой количество экспериментальных переменных равнялось трем (напряжение, температура, скорость). Анализ, проведенный с помощью такой упрощенной модели, показал, что первым шагом должен быть поиск экспериментального или теоретического (либо постулирования) вида модели, удобного для математических преобразований. Так, для случая анализа ползучести показано следующее:
– применяющиеся на практике два основных метода – методы Холломона (или его частный случай – метод Ларсена-Миллера) и Аррениусовское приближение – позволили получить модели, обладающие близкой точностью прогноза;
– в сомножителях обеих моделей, учитывающих влияние температуры деформации, целесообразно учитывать уровень приложенных напряжений (по условиям методики испытаний на ползучесть – всегда начальных);
– учет предыдущего пункта с неизбежностью приводит к появлению в обобщенном уравнении деформации «перекрестного» влияния независимых факторов (как, например, «напряжение σ(1/Т)»).
Эти результаты послужили причиной идеи применения таких же процедур и для нахождения обобщенного математического закона горячей деформации, в котором неизбежно появляется четвертая переменная – степень деформации.
Целью работы является разработка обобщенного математического уравнения для описания больших горячих пластических деформаций, учитывающего одновременное влияние степени деформации φ, скорости деформации φ′ и температуры Т, и не опирающегося на структурно-механические константы материала.
Описание объекта анализа и методики его обработки
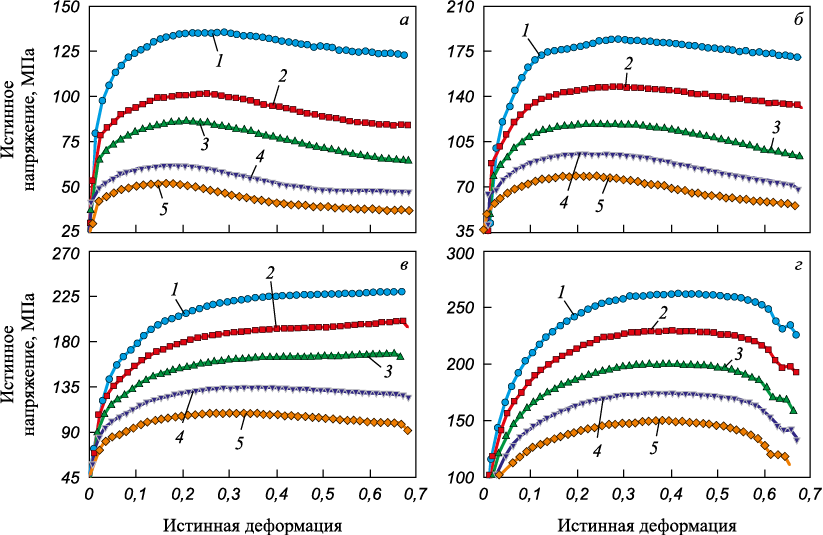
Все исследователи при многофакторном анализе горячей деформации используют результаты опытов на сжатие цилиндрических образцов диаметром порядка 10 мм и отношением высоты к диаметру ~1 – 2. В данном исследовании анализ проведен, используя результаты, описанные в работе [12]. Янг-Хонг Ксиао и Ченг Гуо в своем сообщении представили данные испытаний на сжатие до значений истинной степени деформации ~1 при 1253 – 1453 К и скорости сжатия 0,01 – 10 с\(^–\)1 образцов жаропрочной 12 %-ной хромистой стали 1Cr12Ni3Mo2VNbN. Вид исходных кривых деформации приведен на рис. 1.
Рис. 1. Кривые горячей деформации сжатием в истинных координатах |
Оцифровкой этих кривых с помощью программы Grafula был получен массив экспериментальных данных в виде таблицы, содержащей ~800 строк, в которой в четырех столбцах были записаны данные о деформации, напряжении, скорости деформации и температуры для каждой экспериментальной точки (примерно по 40 точек для каждой из 20 экспериментальных кривых). Независимыми переменными являлись истинная степень деформации φ, истинная скорость деформации φ′, температура Т (К). Зависимой переменной было истинное напряжение S. В таблице приведен фрагмент исходных данных.
Фрагмент массива исходных данных для анализа
|
Результаты работы и их обсуждение
С учетом результатов работ [14; 15], изложенных выше, на первом шаге за основу была взята Аррениусовская зависимость (ОВ). С использованием функции regress из программы Mathcad были получены значения коэффициентов A, B, C, D в уравнении (1.1а). После обратного преобразования выражения (1.1а) из логарифмического вида к прямому (1.1б) получено уравнение
| \[\begin{array}{c}\sigma = 5,633 \cdot {10^{ - 4}}{\varepsilon ^{0,077}}{{\dot \varepsilon }^{0,127}}\exp \left( { - \frac{{66,487}}{{RT}}} \right),\\(R = 8,315{\rm{Дж/моль}} \cdot {\rm{К}}).\end{array}\] | (1.1б) |
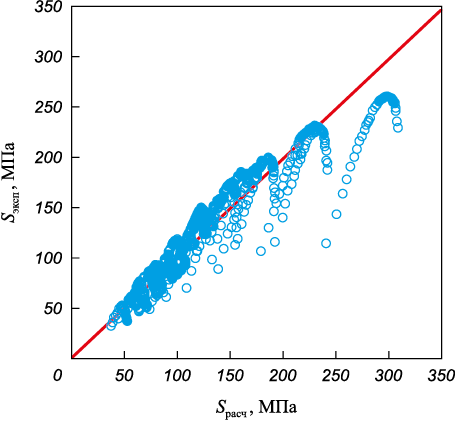
Визуальная оценка качества модели проводилась по графику сравнением экспериментальных значений S с рассчитанными по полученному уравнению (1.1б) (рис. 2).
Рис. 2. Сопоставление расчетных и экспериментальных значений |
Для количественной оценки качества математической модели вычисляли сумму квадратов разностей между расчетными и экспериментальными значениями напряжений с ее нормированием на среднюю величину напряжения S по формуле
| \[Q = \frac{n}{{\sum S }}\sqrt {\sum {\frac{{{{\left( {{S_{{\rm{расч}}}} - {S_{{\rm{эксп}}}}} \right)}^2}}}{{n - 5}}} } .\] | (2) |
Для модели вида (1.1б) этот показатель оказался равен ~14 %.
Сопоставление визуальной и количественной оценок показывает, что несмотря на малую среднюю величину рассеяния прогнозных значений от экспериментальных, для интервалов больших напряжений (это конечные участки кривых сжатия с большими степенями деформации) уравнение (1.1б) дает плохой прогноз (рис. 2).
С целью уточнения вида предполагаемой модели проведен анализ индивидуальных кривых деформации. Поскольку основным математическим методом поиска коэффициентов при переменных был линейный регрессионный анализ с использованием метода наименьших квадратов, предметом анализа были линейные уравнения с логарифмической формой представления переменных. Предварительные опыты (под словом «опыт» понимали различные варианты математических формул связи переменных) по нахождению уравнений, описывающих индивидуальные кривые деформации (каждая такая кривая получена при постоянных значениях температуры и скорости деформации) показали, что для большинства кривых деформации хорошим описанием является уравнение вида
| S = А(φ)B10C(φ) | (3) |
или после логарифмирования
| log(S) = A1 + B1 log(φ) + C1 (φ). | (3a) |
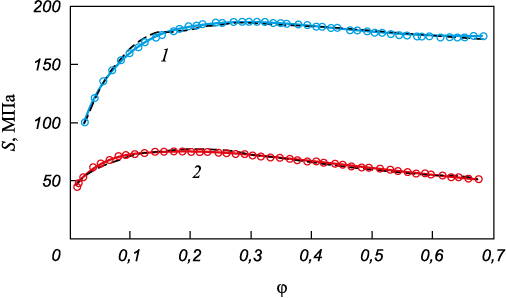
Такое представление позволяет получать значения Q для индивидуальных кривых от 1,5 до 5 % (рис. 3).
Рис. 3. Описание зависимостей S – φ формулой (3): |
Еще больше повышается точность прогноза при включении в выражение (3а) сомножителя в виде частного от деления степени деформации (φ) на логарифм этой величины:
| \[\log (S) = A2 + B2\log (\varphi ) + C2(\varphi ) + \frac{{D2(\varphi )}}{{\log (\varphi )}}.\] | (4) |
Оценка качества таких уравнений по параметру Q составляет 0,5 – 1,7 % (рис. 3), а связь переменных в прямом представлении (уходя от логарифмов) описывается уравнением
| \[S = {\varphi ^{B3}}\exp \left[ {A3 + C3(\varphi ) + \frac{{D3(\varphi )}}{{\log (\varphi )}}} \right].\] | (4а) |
Дальнейшее развитие этой модели состояло в следующем. На кривых деформации, полученных при испытании при низких температурах и (или) высоких скоростях деформации, после точки предела текучести на графиках присутствует протяженный участок значительного роста напряжения с высоким коэффициентом деформационного упрочнения D = dS/dφ. Такая особенность формы кривой может быть учтена введением полинома третьей степени от деформации φ. По этой логике в модель (в логарифмическом ее виде) были введены квадратичный и кубический члены от степени деформации φ:
| \[\begin{array}{c}\log (S) = A4 + B4\log (\varphi ) + C4\log {(\varphi )^2} + D4\log {(\varphi )^3} + \\ + E4(\varphi ) + \frac{{F4(\varphi )}}{{\log (\varphi )}}.\end{array}\] | (4в) |
В прямом представлении это выражение описывается уравнением
| \[S = {\exp ^{A5 + E5(\varphi ) + \frac{{F5(\varphi )}}{{\log (\varphi )}}}}{\varphi ^{B5 + C5\log (\varphi ) + D5{{[\log (\varphi )]}^2}}}.\] | (4г) |
При таком представлении параметр Q для индивидуальных кривых уменьшается до 0,3 – 1,0 %.
С учетом всего вышесказанного была разработана модернизированная математическая модель для описания полной базы данных. Модернизация модели (1.1) в ее логарифмическом представлении (1.1а) состояла в том, что:
– в сомножитель, учитывающий влияние температуры деформации, вводились (под знак экспоненты) слагаемые для учета степени деформации φ и скорости деформации φ′;
– учет взаимного влияния независимых факторов друг на друга осуществлялся добавлением сомножителя (φφ′);
– вводилась зависимость от квадрата и куба степени деформации φ через соответствующие сомножители.
Общий вид уравнения связи переменных после приведения его к линейному виду логарифмированием выглядит следующим образом:
| \[\begin{array}{c}\log (S) = A + B\log (\varphi ) + C{[\log (\varphi )]^2} + D{[\log (\varphi )]^3} + \\ + E\log (\varphi ') + F\log (\varphi )\log (\varphi ') + G\left( {\frac{\varphi }{{\varphi '}}} \right) + \\ + \frac{{H + K\varphi + M\log (\varphi ) + N\log (\varphi ') + P\log (\varphi )\log (\varphi ')}}{T}.\end{array}\] | (5) |
Нахождение коэффициентов A – P уравнения (5), обеспечивающее минимум суммы квадратов разностей рассчитанных Sрасч и экспериментальных значений Sэксп , проведенное в программе Machcad, позволило получить искомое уравнение связи в виде
| \[\begin{array}{c}\log (S) = - 0,738 - 1,311\log (\varphi ) - 0,564{[\log (\varphi )]^2} - \\ - 0,13{[\log (\varphi )]^3} + 0,584\log (\varphi ') - \\ - 8,779 \cdot {10^{ - 4}}\log (\varphi )\log (\varphi ') - 1,18 \cdot {10^{ - 3}}\left( {\frac{\varphi }{{\varphi '}}} \right) + \\ + \frac{{3,727 \cdot {{10}^3} + 82,351\varphi + 1,096 \cdot {{10}^{ - 3}}\log (\varphi )}}{T} + \\ + \frac{{593,8\log (\varphi ') + 76,6\log (\varphi )\log (\varphi ')}}{T},\end{array}\] | (6) |
которое может быть приведено к прямому виду:
| \[\begin{array}{c}S = {10^{ - 0,738}}{(\varphi ')^{0,584}} \times \\ \times {\varphi ^{ - 1,311 - 0,564\log (\varphi ) - 0,131{{[\log (\varphi )]}^2} - 8,779 \cdot {{10}^{ - 4}}\log (\varphi ')}} \times \\ \times \exp \left[ {\frac{{8583,3 + 198,7\varphi + 2524\log (\varphi )}}{T} - } \right.\\ - \frac{{1367,5\log (\varphi ') + 176,4\log (\varphi )\log (\varphi ')}}{T} - \\ - \left. {2,718 \cdot {{10}^{ - 3}}\left( {\frac{\varphi }{{\varphi '}}} \right)} \right],\end{array}\] | (6а) |
или с обособлением температурной части:
| \[\begin{array}{c}S = {10^{ - 0,738}}{(\varphi ')^{0,584}} \times \\ \times {\varphi ^{ - 1,311 - 0,564\log (\varphi ) - 0,131{{[\log (\varphi )]}^2} - 8,779 \cdot {{10}^{ - 4}}\log (\varphi ')}} \times \\ \times \exp \left[ { - 2,718 \cdot {{10}^{ - 3}}\left( {\frac{\varphi }{{\varphi '}}} \right)} \right] \times \\ \times \exp \left[ {\frac{{8583,3 + 198,7\varphi + 2524\log (\varphi )}}{T} - } \right.\\ - \left. {\frac{{1367,5\log (\varphi ') + 176,4\log (\varphi )\log (\varphi ')}}{T}} \right].\end{array}\] | (6б) |
Графическая иллюстрация совпадений расчетных и экспериментальных значений S приведена на рис. 4. Показатель качества такой модели Q = 6,1 %, что много лучше, чем по исходной модели как качественно, так и количественно (сравнить с рис. 2).
Рис. 4. Сопоставление расчетных и экспериментальных значений |
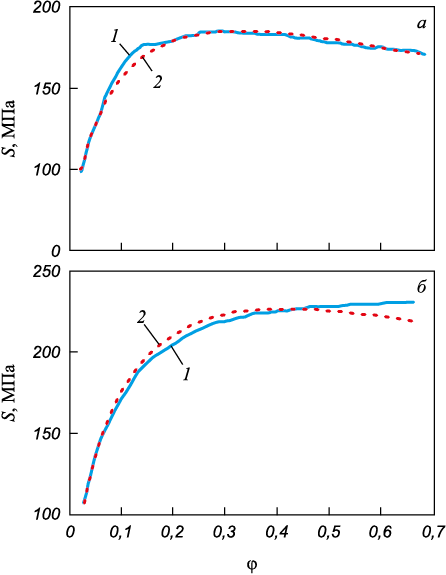
Полученное уравнение (6а) позволяет прогнозировать вид кривой деформации для различных сочетаний φ, φ′ и Т. На рис. 5 приведены примеры таких графиков в сопоставлении с экспериментальными кривыми. Представленные графики иллюстрируют «хорошее» и «не очень хорошее» совпадение расчетных и экспериментальных кривых.
Рис. 5. Сопоставление экспериментальных кривых деформации (1) |
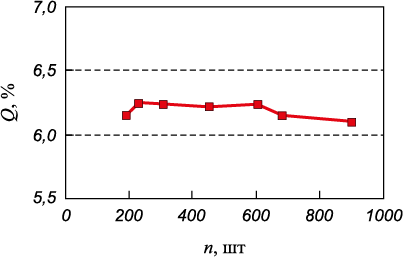
Из теории статистики известно [16], что увеличение размера выборки экспериментальных данных может приводить к улучшению точности описания математической модели (уменьшению ее дисперсии). Для проверки этого тезиса искусственно последовательно уменьшалось число исходных данных (число строк в полной матрице) от ~900 до ~200 и проводился расчет показателя качества модели Q. Результаты этих расчетов представлены на рис. 6. Видно, что изменение объема выборки экспериментальных данных примерно в 4 раза (от 900 до 200) значимо не сказывается на прогностическом качестве модели (6а).
Рис. 6. Изменение показателя Q обобщенной модели деформации в форме (6а) |
Возможно, такой неожиданный результат отражает тот факт, что определяющими с точки зрения формы моделируемой кривой являются лишь несколько характерных точек (по этому признаку близкой по методике является упомянутая выше методика Джонсона-Кука).
Важной проверкой работоспособности разработанной модели является ее проверка на иных исходных базах данных. По описанной выше методике были обработаны результаты испытаний на горячее сжатие материалов из других групп: жаропрочного никелевого сплава Ni33Cr27Fe35Mo3,5Mn1Cu0,6 из группы инконелей [17], жаропрочных никелевых сплавов [18] и сплава Ni56Cr24Co14Mo0,5W1Nb1,5Al1,5Ti1,5 из группы нимоников [19], кобальтовых сплавов [20; 21], ферритных жаростойких хромистых сталей типа Х12 – Х27 [22], жаропрочной 9 %-ной хромистой ДУО-стали [23] и стали 20Х13 [24]. Найдено, что разработанный вид математической модели применим и для этих случаев. При этом подразумевается, что для всех этих случаев номенклатура и вид сомножителей в формуле связи – единые для всех изученных сплавов, а коэффициенты при них, естественно, различные. Качество прогноза, оцениваемое показателем Q, составляло от 3 до 11 %.
Выводы
Предложен вид обобщенной математической зависимости в мультипликативной форме, позволяющей описывать связь между напряжением, деформацией, ее скоростью и температурой при большой (до степени истинной деформации 0,8) горячей (0,60 – 0,85Т/Тпл) деформации со скоростью от 0,01 до 10 с–1, и обеспечивающей прогноз деформирующего усилия с точностью ~6 % без использования априорных (табличных) или предварительно определяемых структурных, силовых и энергетических характеристик.
Использованные в разработанной математической форме сочетания сомножителей отражают экспериментально наблюдаемые взаимозависимости независимых (φ, φ′, Т) факторов и особенности внешнего вида линий диаграмм деформации.
Установлено, что найденный вид математического описания горячей деформации применим к анализу процессов горячей деформации самых разнообразных металлических материалов, при этом точность прогнозных характеристик напряжения деформирования составляет 3 – 11 %.
Полученные данные позволяют проводить анализ не только для результатов испытаний с фиксированной истинной скоростью деформации φ′, что методически довольно сложно, но и результатов опытов, проведенных по традиционной методике с постоянной условной скоростью деформации \(\dot \varepsilon \) (в процессе таких опытов величина φ′ не постоянна).
Список литературы
1. Штремель М.А. Прочность сплавов. Ч. 2. Деформация. Москва: МИСИС; 1997:527.
2. Hollomon J.H. Tensile deformation. Trans AIME. 1945; 162:268–290.
3. Розенберг В.М. Основы жаропрочности металлических материалов. Москва: Металлургия; 1973:328.
4. Ludwigson D.C. Modified stress-strain relation for FCC metals and alloys. Metallurgical Transactions A. 1971;2(10): 2825–2828. https://doi.org/10.1007/BF02813258
5. Берштейн М.Л., Займовский В.А. Механические свойства металлов. Москва: Металлургия; 1979:496.
6. Zener C., Hollomon J. H. Effect of strain rate upon plastic flow of steel. Journal of Applied Physics. 1944;15(1):22–32. https://doi.org/10.1063/1.1707363
7. Bird J.E., Mukherjee A.K., Dorn J.E. Experimental correlations between high-temperature creep behavior and structure. In: Quantitative Relation Between Properties and Microstructure. Brandon D.G., Rosen A. eds. Jerusalem University Press; 1969:255–342.
8. Johnson G.R., Cook W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Engineering Fracture Mechanics. 1985;21(1):31–48. https://doi.org/10.1016/0013-7944(85)90052-9
9. Sellars C.M., McTegart W.J. Cavity growth mechanisms during creep. Acta Metallurgical. 1966;14:1136–1138.
10. Sun C., Liu G., Zhang Q., Li R., Wang L. Determination of hot deformation behavior and processing maps of IN 028 alloy using isothermal hot compression test. Materials Science and Engineering: A. 2014;595:92–98. https://doi.org/10.1016/j.msea.2013.10.051
11. Fang B., Ji Z., Liu M., Tian G., Jia C., Zeng T., Benfu HU, Wang C. Study on constitutive relationships and processing maps for FGH96 alloy during two-pass hot deformation. Materials Science and Engineering: A. 2014;590:255–261. https://doi.org/10.1016/j.msea.2013.10.034
12. Xiao Y.-H., Guo C. Constitutive modeling for high temperature behavior of 1Cr12Ni3Mo2VNbN martensitic steel. Materials Science and Engineering: A. 2011;528(15): 5081–5087. https://doi.org/10.1016/j.msea.2011.03.050
13. Zerilli F.J., Armstrong R.W. Dislocation-mechanics-based relations for material dynamics calculations. Journal of Applied Physics. 1987;61(5):1816–1825. https://doi.org/10.1063/1.338024
14. Беломытцев М.Ю. Экспериментальный анализ закономерностей ползучести жаропрочной ферритно-мартенситной стали. Деформация и разрушение материалов. 2019;(10):31–41.
15. Беломытцев М.Ю., Моляров В.Г. Исследование сопротивления ползучести ферритно-мартенситной стали 16Х12МВСФБР (ЭП-823). Известия вузов. Черная металлургия. 2019;62(4):290–302. https://doi.org/10.17073/0368-0797-2019-4-290-302
16. Мельниченко А.С. Статистический анализ в металлургии и материаловедении: Учебник. Москва: Издательский Дом МИСИС; 2009:268.
17. Wang L., Liu F., Cheng J.J., Zuo Q., Chen C.F. Hot deformation characteristics and processing map analysis for Nickel-based corrosion resistant alloy. Journal of Alloys and Compounds. 2015;623:69–78. https://doi.org/10.1016/j.jallcom.2014.10.034
18. Pan Q.L., Li B., Wang Y., .Zhang Y.W., Yin Z.M. Characterization of hot deformation behavior of Ni-base superalloy Rene’41 using processing map. Materials Science and Engineering: A. 2013;585:371–378. https://doi.org/10.1016/j.msea.2013.07.066
19. Wu Y., Zhang M., Xie X., Dona J., Lin F., Zhao S. Hot deformation characteristics and processing map analysis of a new designed nickel-based alloy for 700 °C A-USC power plant. Journal of Alloys and Compounds. 2016;656:119–131. https://doi.org/10.1016/j.jallcom.2015.09.219
20. Kumar V.A., Gupta R.K., Murty S.V.S. Narayana, Prasad A.D. Hot workability and microstructure control in Co20Cr15W10Ni cobalt based superalloy. Journal of Alloys and Compounds. 2016;676:527–541. https://doi.org/10.1016/j.jallcom.2016.03.186
21. Kartica Ika, Matsumoto H., Chiba A. Deformation and microstructure evolution in Co-Ni-Cr-Mo superalloy during hot working. Metallurgical and Materials Transactions A. 2009;40:1457–1468. https://doi.org/10.1007/s11661-009-9829-x
22. Mehtonen S.V., Karjalainen L.P., Porter D.A. Modeling of the high temperature flow behavior of stabilized 12 – 27wt% Cr ferritic stainless steels. Materials Science and Engineering: A. 2014;607:44–52. https://doi.org/10.1016/j.msea.2014.03.124
23. Zhang G., Zhou Z., Sun H., Zou L., Wang M., Li S. Hot deformation behavior and processing map of a 9Cr ferritic/martensitic ODS steel. Journal of Nuclear Materials. 2014;455(1-3):139–144. https://doi.org/10.1016/j.jnucmat.2014.05.043
24. Ахмедьянов А.М., Рущиц С.В., Смирнов М.А. Физическое и математическое моделирование горячей деформации стали 20Х13. Вестник ЮУрГУ. Серия «Металлургия». 2013;13(2):116–124.
Об авторе
М. Ю. БеломытцевРоссия
Михаил Юрьевич Беломытцев, д.т.н., профессор кафедры металловедения и физики прочности
Россия, 119049, Москва, Ленинский пр., 4
Рецензия
Для цитирования:
Беломытцев М.Ю. Вид обобщенной математической модели для описания больших горячих деформаций. Известия высших учебных заведений. Черная Металлургия. 2024;67(5):616-624. https://doi.org/10.17073/0368-0797-2024-5-616-624
For citation:
Belomyttsev M.Yu. Type of generalized mathematical model for describing large hot deformations. Izvestiya. Ferrous Metallurgy. 2024;67(5):616-624. https://doi.org/10.17073/0368-0797-2024-5-616-624
JATS XML