Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 2

В. И. Одиноков; А. И. Евстигнеев; Э. А. Дмитриев; А. Н. Намоконов; А. А. Евстигнеева; Д. В. Чернышова

doi:10.17073/0368-0797-2024-4-463-470

Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 2

В. И. Одиноков, А. И. Евстигнеев, Э. А. Дмитриев, А. Н. Намоконов, А. А. Евстигнеева, Д. В. Чернышова

https://doi.org/10.17073/0368-0797-2024-4-463-470

Полный текст:

сгенерировать QR код

Содержание

Перейти к:

Аннотация

В статье приведены результаты численного решения задачи по моделированию процесса возможного трещинообразования в оболочковой форме (ОФ) шарообразной конфигурации при заливке в нее жидкой стали и охлаждении затвердевающей отливки. Численная схема осесимметричной задачи и алгоритм решения были приведены в части 1. Трещиностойкость оценивается по величине нормальных напряжений в керамической ОФ в процессе ее совместного охлаждения с затвердевающей отливкой. При детальном анализе результатов были учтены поля перемещений, напряжений, температур как в сферической ОФ, так и в нарастающей корочке затвердевшего металла. При решении учитывалось изменение модуля сдвига материала формы от температуры, и была дана оценка этого уточнения. Задачу решали двумя способами. Первый – с постоянным модулем сдвига ОФ; второй – с модулем сдвига ОФ, зависящим от температуры. Между этими вариантами есть существенная разница в величине нормальных напряжений, возникающих в ОФ. Авторы проанализировали стойкости ОФ сферической геометрии от внешних воздействий со стороны опорного наполнителя (ОН) оболочковой формы и заливочной воронки. Была решена задача по определению контактной и свободной поверхностей на границе ОФ и ОН. Результаты решения задачи представлены графически в виде эпюр напряжений, температур по исследуемой области в разных ее сечениях и временных интервалах охлаждения ОФ и нарастающей корочки металла. Показана роль сжимающих нормальных напряжений σ₂₂, σ₃₃ на поверхности соприкосновения ОФ с жидким металлом в начальный момент охлаждения на вероятность трещинообразования в сферической форме. Уровень напряженно-деформированного состояния в сферической ОФ при охлаждении в ней стальной отливки существенно определяется зависимостью модуля сдвига ОФ от температуры.

Ключевые слова

литье по выплавляемым моделям, оболочковая форма, напряженное состояние, моделирование, трещинообразование

Для цитирования:

Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Намоконов А.Н., Евстигнеева А.А., Чернышова Д.В. Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 2. Известия высших учебных заведений. Черная Металлургия. 2024;67(4):463-470. https://doi.org/10.17073/0368-0797-2024-4-463-470

For citation:

Odinokov V.I., Evstigneev A.I., Dmitriev E.A., Namokonov A.N., Evstigneeva A.A., Chernyshova D.V. Stress-strain state of ceramic shell mold during formation of spherical steel casting in it. Part 2. Izvestiya. Ferrous Metallurgy. 2024;67(4):463-470. https://doi.org/10.17073/0368-0797-2024-4-463-470

Введение

Ранее исследования по влиянию напряженно-деформированного состояния (НДС) на ее трещиностойкость при заливке жидким металлом и охлаждении совместно с затвердевающей отливкой проводились на оболочковой форме (ОФ) для литья по выплавляемым моделям (ЛВМ) в виде стояка, имеющего как цилиндрическую, так и сферическую форму (зумпф). Проведено множество теоретических и экспериментальных исследований по установлению особенностей напряженно-деформированного состояния (НДС) керамической оболочковой формы и получаемых отливок в литье по выплавляемым моделям: по влиянию на НДС материалов выплавляемых моделей [1; 2], формы и геометрии ОФ [3; 4], толщины стенки формы [5; 6], материала формы [7; 8], геометрии отливок [9 ‒ 11], методов испытаний формы на прочность и пр. [12; 13].

Математическое моделирование рассматриваемых процессов также представлено в других работах (методы моделирования [14], исследований [15 ‒ 17], с использованием численного моделирования [18 ‒ 20], специальных математических моделей [21 ‒ 23] и программных средств [24; 25].

Вызывает как научный, так и практический интерес изготовление отливок шаровой и сферической форм при помощи ЛВМ, а значит, и стойкость ОФ к трещинообразованию при формировании в ней таких отливок. Именно на решение этой задачи и направлены материалы настоящей работы.

В работе [26] приведены общая постановка задачи по построению математической модели по определению НДС и температуры в ОФ при охлаждении в ней сферической отливки, численная схема и алгоритм решения задачи с использованием разработанных комплексов программ [27; 28]. В настоящей работе представлены результаты теоретического и численного исследований решения поставленной задачи.

Основная часть

В работе [26] изложена общая постановка задачи по охлаждению шарообразной отливки в оболочковой форме.

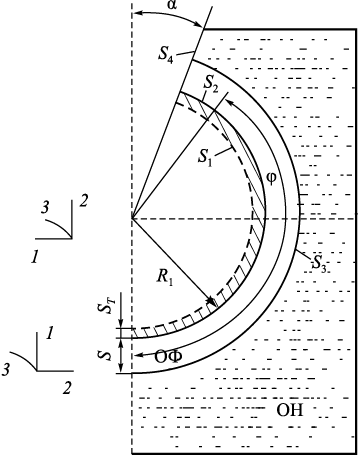
На рис. 1 представлена расчетная схема исследуемого процесса с учетом осевой симметрии (здесь угол α определяет величину окна литниковой воронки, а угол φ ‒ величину охвата ОФ опорным наполнителем (ОН)).

Рис. 1. Расчетная схема шарообразной ОФ,
заформованной в опорный наполнитель и залитой
жидким металлом, с учетом осевой симметрии:
ЖМ – жидкий металл; ТМ ‒ твердый металл;
ОФ – оболочковая форма; ОН – опорный наполнитель;
S₁ – внутренняя поверхность контакта жидкого и затвердевшего металла;
S₂ – внутренняя поверхность контакта затвердевшего металла и оболочковой формы;
S₃ – внешняя поверхность оболочковой формы;
S₄ – свободная поверхность торца литниковой чаши ОФ;
R₁ ‒ радиус шарообразной отливки;
S – толщина оболочковой формы;
S_T – толщина корочки затвердевшего металла;
α ‒ угол наклона литниковой воронки;
φ – угол охвата поверхности оболочковой формы опорным наполнителем

Исходные данные

Геометрические параметры: S = 5 мм, R₁ = 20 мм.

Временные интервалы ∆τ_n: 0,1; 1,0; 2,0; 4,0; 5,0; 5,0; 5,0; 10,0; 10,0; 1,0; 2,0; 5,0; 1,0; 1,0; 3,0; 3,0; 5,0; 10,0; 10,0 с; параметр трения на поверхности S₃ (рис. 1) принимается ψ = 0,001.

Разбиение области: N₁×N₂ = 10×30.

Приняты следующие физические параметры разливаемой стали при температуре θ > 1000 °C (\(\theta _{\rm{м}}^*\) = 1500 °C): G = 1000 кг/мм² (модуль сдвига); α = 12∙10\(^‒\)⁶ °С\(^‒\)¹ (коэффициент линейного расширения); λ = 0,0298 Вт/(мм∙°C) (коэффициент теплопроводности); L = 270·10³ Дж/кг (скрытая теплота плавления); C = 444 Дж/(кг·°C) (удельная теплоемкость); γ = 7,80·10\(^‒\)⁶ кг/мм³ (удельная масса); θ_к = 1450 °C (температура кристаллизации).

Физические свойства керамической формы: G_ф = 2910 кг/мм²; α = 0,51·10\(^‒\)⁶ °С\(^‒\)¹; λ = 0,000812 Вт/(мм·°C); C = 840 Дж/(кг·°C); γ = 2,0·10\(^‒\)⁶ кг/мм³.

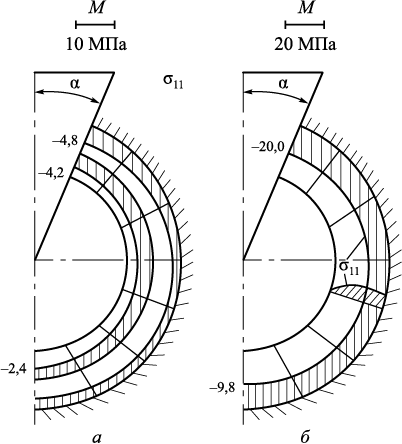
Некоторые результаты теоретического исследования показали [29], что при охлаждении стали в ОФ с величиной α 10 и 30° и φ = (180 – α) имеют место значительные сжимающие напряжения σ₂₂, σ₃₃, которые могут превосходить предел прочности керамики при сжатии. Причем при α = 30° напряжения σ_ii, i = 2, 3 несколько меньше по абсолютной величине, чем при α = 10°. На рис. 2 приведены эпюры нормальных напряжений σ₁₁ в ОФ при α = 10° поз. а – через 7,1 с охлаждения, поз. б ‒ через 51,1 с.

Рис. 2. Эпюры нормальных напряжений σ₁₁ в ОФ при α = 10°
при времени охлаждения отливки 7,1 с (а) и 51,1 с (б)

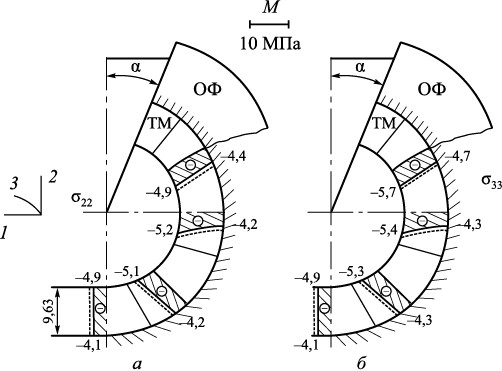
На рис. 3 приведены эпюры напряжений σ₂₂ и σ₃₃ в образующейся корочке металла через 60,1 с охлаждения отливки; сплошными линиями показаны эпюры при α = 30°; штриховыми ‒ α = 10°.

Рис. 3. Эпюры нормальных напряжений σ₂₂ (а) и σ₃₃ (б)
в образующей корочке металла при α = 30° (сплошные линии)
и α = 10° (штриховые линии) и времени охлаждения отливки 60,1 с

Величина σ₂₂, σ₃₃ на поверхности, примыкающей к жидкому металлу, больше (по модулю), чем на поверхности ОФ, это объясняется тем, что модуль сдвига G_m образующегося твердого металла принят постоянным (1000 кг/мм²), независящим от температуры. Также как и в ОФ, напряжения σ₂₂, σ₃₃ – сжимающие и при α = 10° они больше, чем при α = 30°.

На рис. 4, а показаны эпюры напряжений σ₁₁ в корочке закристаллизовавшегося металла через 60,1 с. Напряжения σ₁₁ – сжимающие по всему сечению: сплошными линиями обозначены σ₁₁ при α = 30°, штриховыми – при α = 10°.

Рис. 4. Эпюры нормальных напряжений σ₁₁ (а)
в закристаллизовавшейся корочке металла через время
охлаждения отливки 60,1 с и кривые роста величины корочки металла (S)
и напряжений σ₃₃ (б) со временем охлаждения

На рис. 4, б показаны кривые роста величины корочки S и напряжения σ₃₃ со временем охлаждения. С увеличением угла α нормальные напряжения незначительно уменьшаются (по модулю).

Дальнейшее увеличение α не имеет смысла, поскольку идет нарастание корочки металла при незначительном изменении нормальных напряжений.

Результаты получены при постоянной (средней) величине модуля сдвига ОФ (G_ф).

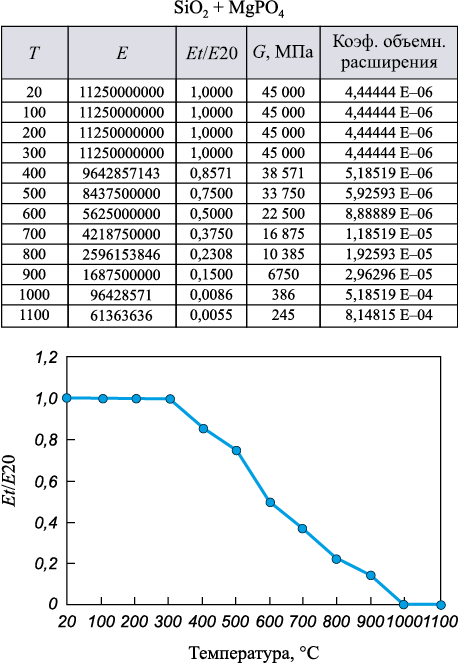
Как следует из работы [29], температура в ОФ, примыкающей к кристаллизующемуся металлу, очень высока (порядка 1300 °C). При такой температуре керамика находится практически в размягченном состоянии, а значит и модуль сдвига в ней будет намного ниже, чем средняя величина G_ф оболочковой формы. Воспользуемся экспериментальными данными (рис. 5), полученными в работе [30] при испытании керамических образцов, выполненных из связующего материала (SiO₂ + MgPO₄).

Рис. 5. Экспериментальные данные при испытании керамических образцов,
выполненных из связующего материала (SiO₂ + MgPO₄)

Аппроксимируя результаты, представленные на рис. 5, получим:

G_ф = 6412 – 6,37θ, кг/мм² при 300 °С < θ < 1000 °С;

G_ф = 40 кг/мм² при θ ≥ 1000 °С;

G_ф = 4500 кг/мм² при θ < 300 °С.

Результаты решения с изменяющимся от температуры модулем сдвига ОФ приведены на рис. 6 при α = 10° в виде эпюр σ_ii, i = 1, 2, 3 при τ = 1,12 с – сплошные линии; τ = 7,12 с – штриховые линии.

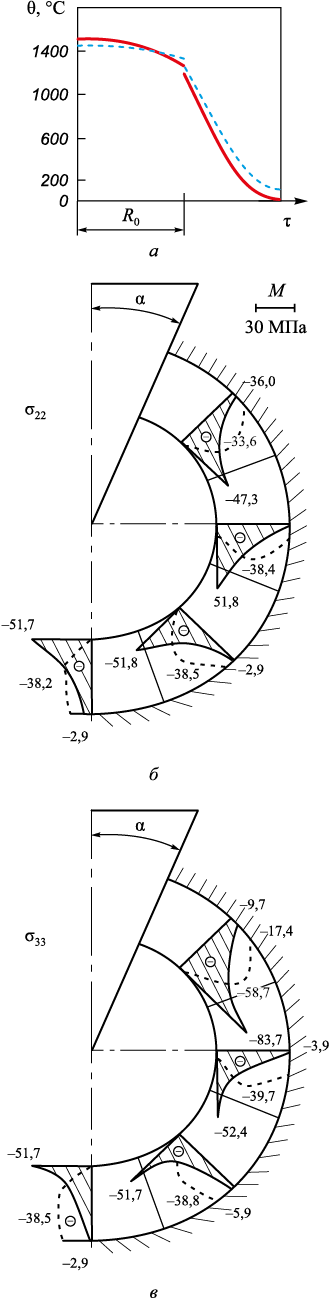
Рис. 6. Поле температур (a), эпюры нормальных напряжений σ₂₂ (б) и σ₃₃ (в)
в ОФ при α = 10° и времени охлаждения
отливки 1,12 с () и 7,12 c ()

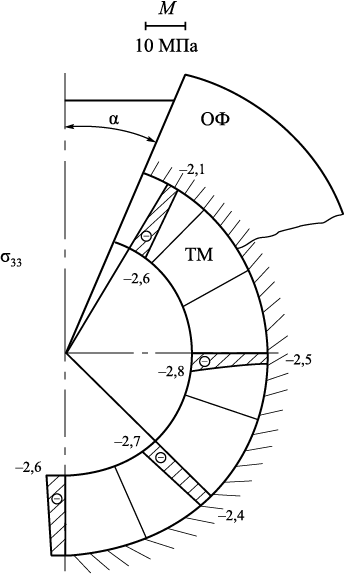
При термическом ударе и времени охлаждения τ = 1,12 с напряжения σ₂₂, σ₃₃ имеют наибольшие значения (по абсолютной величине) в ОФ в зоне контакта с металлом, но уже резко меняются со временем охлаждения. Все нормальные напряжения – сжимающие. Напряжения σ₃₃ в образующейся корочке S = 6 мм через τ = 7,12 с приведены на рис. 7.

Рис. 7. Эпюры нормальных напряжений σ₃₃ в образующейся
металлической корочке (S = 6 мм) при времени охлаждения отливки 7,12 c

При дальнейшем охлаждении напряжения σ_ii уменьшаются.

Наиболее опасен к разрушению начальный период охлаждения (0 < τ < 8 с) (рис. 6).

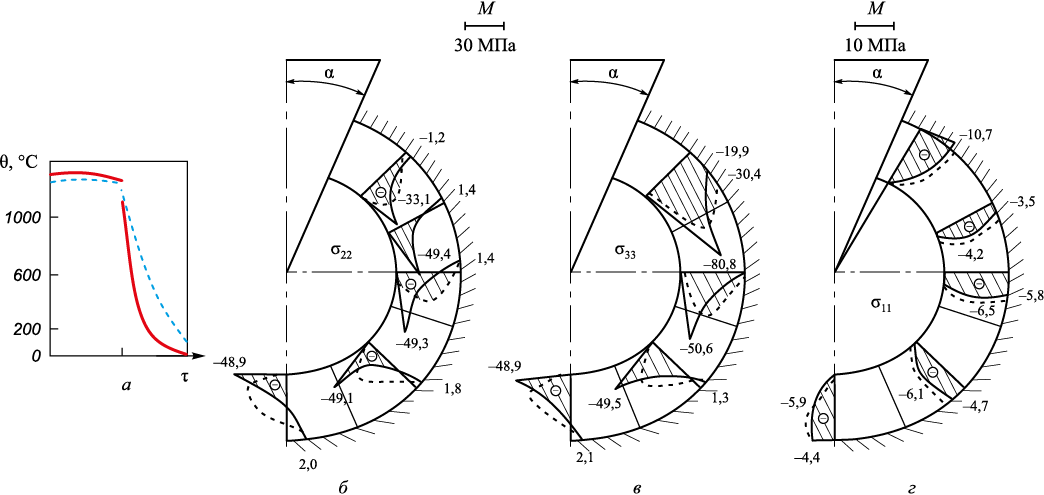
На рис. 8, 9 приведены результаты расчета при α = 30°, τ = 1,12 с (сплошные линии); τ = 7,12 с (штриховые линии).

Рис. 8. Поле температур (a), эпюры нормальных напряжений σ₂₂ (б), σ₃₃ (в) и σ₁₁ (г)
в ОФ при α = 30°
через время охлаждения отливки 1,12 с () и 7,12 c ()

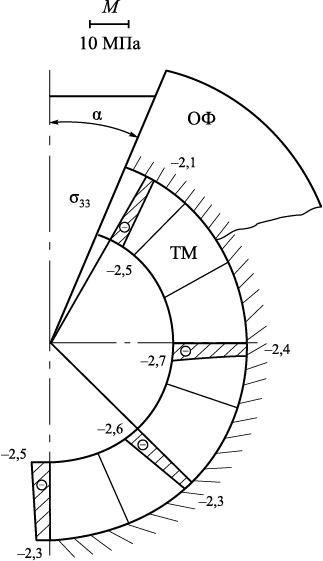
Рис. 9. Эпюры нормальных напряжений σ₃₃ в образующейся
корочке металла через время охлаждения отливки 7,12 с (α = 30°)

Как видим, картина примерно та же, но значения σ_ii, i = 1, 2, 3 несколько ниже, чем при α = 10°, даже появились небольшие растягивающие напряжения σ₂₂, σ₃₃ в ОФ на стыке с ОН (рис. 8). В корочке металла S = 6 мм при τ = 7,12 с приведены напряжения σ₃₃ (рис. 9), они также ниже, чем при α = 10° (рис. 3, б).

Дальнейшее охлаждение показывает, что нормальные напряжения падают, а эпюры σ_ii при τ = 32,12 и 52,12 с близки друг к другу.

Что касается вопроса влияния материала цилиндрической ОФ на ее стойкость, то такие результаты были представлены в предыдущих работах авторов, где в рассматриваемом случае наиболее опасными для возможного трещинообразования в ОФ являются растягивающие нормальные напряжения σ₂₂ в наружном (внешнем) слое оболочки, контактирующем с опорным наполнителем.

Учет зависимости модуля сдвига в ОФ от температуры существенно влияет на напряженно-деформированное состояние в ОФ при охлаждении в ней стальной отливки. При принятых внешних воздействиях на процесс охлаждения металла в сферической ОФ стойкость ее к разрушению в начальный момент заливки является проблематичной.

Выводы

Осуществлено более корректное решение задачи с учетом изменения модуля сдвига материала формы от температуры, что существенно отразилось на результатах решения. Анализ НДС в ОФ сферической формы при заливке в нее стальной отливки показал, что опасными являются сжимающие напряжения σ₂₂, σ₃₃ на поверхности соприкосновения ОФ с жидким металлом в начальный момент охлаждения. Значительные сжимающие напряжения σ₁₁ (до 10 МПа) на поверхности соприкосновения ОФ с ОН указывают на возможность и необходимость дальнейшего теоретического исследования данного процесса посредством моделирования величины поверхности охвата ОН сферической ОФ.

Список литературы

1. Bansode S.N., Phalle V.M., Mantha S.S. Optimization of process parameters to improve dimensional accuracy of investment casting using Taguchi approach. Advances in Mechanical Engineering. 2019;11(4):1–12. https://doi.org/10.1177/1687814019841460

2. Mittal Y.G., Kamble P., Gote G., Patil Y., Patel A. K., Bernard A., Karunakaran K.P. Mathematical modelling of pattern sublimation in rapid ice investment casting. International Journal of Metalcasting. 2022;16(2):1002–1009. http://dx.doi.org/10.1007/s40962-021-00665-w

3. Kanyo J.E., Schafföner S., Uwanyuze R.Sh., Leary K.S. An overview of ceramic molds for investment casting of nickel superalloys. Journal of the European Ceramic Society. 2020;40(15):4955–4973. https://doi.org/10.1016/j.jeurceramsoc.2020.07.013

4. Rafique M.M.A., Iqbal J. Modeling and simulation of heat transfer phenomena during investment casting. International Journal of Heat and Mass Transfer. 2009;52(7–8):2132–2139. http://doi.org/10.1016/j.ijheatmasstransfer.2008.11.007

5. Singh R. Mathematical modeling for surface hardness in investment casting applications. Journal of Mechanical Science and Technology. 2012;26:3625–3629. http://dx.doi.org/10.1007/s12206-012-0854-0

6. Jafari H., Idris M. H., Ourdjini A. Effect of thickness and permeability of ceramic shell mould on in situ melted AZ91D investment casting. Applied Mechanics and Materials. 2014;465–466:1087–1092. http://dx.doi.org/10.4028/www.scientific.net/AMM.465-466.1087

7. Bansode S.N., Phalle V.M., Mantha S. Taguchi approach for optimization of parameters that reduce dimensional variation in investment casting. Archives of Foundry Engineering. 2019;19(1):5–12. https://dx.doi.org/10.24425/afe.2018.125183

8. Pattnaik S., Karunakar D.B., Jha P.K. Developments in investment casting process ‒ A review. Journal of Materials Processing Technology. 2012;212(11):2332–2348. https://doi.org/10.1016/j.jmatprotec.2012.06.003

9. Zhang J., Li K.W., Ye H.W., Zhang D.Q., Wu P.W. Numerical simulation of solidification process for impeller investment casting. Applied Mechanics and Materials. 2011;80–81: 961–964. https://doi.org/10.4028/www.scientific.net/AMM.80-81.961

10. Dong Y.W., Li X.L., Zhao Q., Jun Y., Dao M. Modeling of shrinkage during investment casting of thin walled hollow turbine blades. Journal of Materials Processing Technology. 2017;244:190–203. https://doi.org/10.1016/j.jmatprotec.2017.01.005

11. Rakoczy Ł., Cygan R. Analysis of temperature distribution in shell mould during thinwall superalloy casting and its effect on the resultant microstructure. Archives of Civil and Mechanical Engineering. 2018;18(4):1441–1450. https://doi.org/10.1016/j.acme.2018.05.008

12. Yameng W., Zhigang L. The design of testing methods for strength of ceramic shell mold in investment casting. Proceedings of the Asia-Pacific Conf. on Intelligent Medical 2018 & Int. Conf. on Transportation and Traffic Engineering. 2018;336–341. https://doi.org/10.1145/3321619.3321686

13. Kolczyk J., Zych J. High temperature strength of ceramic moulds applied in the investment casting method. Archives of Foundry Engineering. 2011;11(3):121–124.

14. Anglada E., Meléndez A., Maestro L., Domínguez I. Finite element model correlation of an investment casting process. Materials Science Forum. 2014;797:105–110. http://dx.doi.org/10.4028/www.scientific.net/MSF.797.105

15. Liu C., Sun J., Lai X., He B., Li F. Influence of complex structure on the shrinkage of part in investment casting process.The International Journal of Advanced Manufacturing Technology. 2015;77:1191–1203. https://doi.org/10.1007/s00170-014-6523-y

16. Liu C., Wang F., Jin S., Li F., Lai X. Permafrost analysis methodology (PAM) for ceramic shell deformation in the firing process. International Journal of Metalcasting. 2019;13(4):953–968. http://dx.doi.org/10.1007/s40962-019-00317-0

17. Everhart W.A., Lekakh S.N., Richards V., Chen J., Li H., Chandrashekhara K. Corner strength of investment casting shells. International Journal of Metalcasting. 2013;7:21‒27. https://doi.org/10.1007/BF03355541

18. Sabau A.S. Numerical simulation of the investment casting process. Transactions of American Foundry Society. 2005;113:407–417.

19. Zheng K., Lin Y., Chen W., Liu L. Numerical simulation and optimization of casting process of copper alloy water-meter shell. Advances In Mechanical Engineering. 2020;12(5):1–12. http://dx.doi.org/10.1177/1687814020923450

20. Manzari M.T., Gethin D.T., Lewis R.W. Optimisation of heat transfer between casting and mould. International Journal of Cast Metals Research. 2000;13(4):199‒206. https://doi.org/10.1080/13640461.2000.11819402

21. Rafique M.M.A., Shah U. Modeling and simulation of heat transfer phenomenon related to mold heating during investment casting. Engineering. 2020;12(5):291–314. http://dx.doi.org/10.4236/eng.2020.125024

22. Dong Y., Bu K., Zhang D. Numerical simulation of displacement field of solidification process for investment casting. In: 2008 Asia Simulation Conf. – 7th Int. Conf. on System Simulation and Scientific Computing. 2008:715–720. https://doi.org/10.1109/asc-icsc.2008.4675453

23. Upadhya G.K., Das S., Chandra U., Paul A.J. Modelling the investment casting process: a novel approach for view factor calculations and defect prediction. Applied Mathematical Modelling. 1995;19(6):354–362. https://doi.org/10.1016/0307-904X(95)90001-O

24. Khan M.A.A., Sheikh A.K. Simulation tools in enhancing metal casting productivity and quality: A review. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture. 2016;230(10):1799–1817. https://doi.org/10.1177/0954405416640183

25. Banerjee S., Sutradhar G. Analysis of casting defects in investment casting by simulation. Advances in Materials, Mechanical and Industrial Engineering: Selected Contributions from the First Int. Conf. on Mechanical Engineering, Jadavpur University, Kolkata, India. Springer International Publishing. 2019:247–271. http://dx.doi.org/10.1007/978-3-319-96968-8_12

26. Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Намоконов А.Н., Евстигнеева А.А., Чернышова Д.В. Напряженно-деформированное состояние керамической оболочковой формы при формировании в ней стальной шарообразной отливки. Часть 1. Известия вузов. Черная металлургия. 2024;67(2):211‒218. https://doi.org/10.17073/0368-0797-2024-2-211-218

27. Одиноков В.И., Прокудин А.Н., Сергеева А.М., Севастьянов Г.М. Свидетельство о государственной регистрации программы для ЭВМ № 2012111389. ОДИССЕЙ. Зарегистрировано в Реестре программ для ЭВМ 13.12.2012.

28. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И., Иванкова Е.П. Свидетельство о государственной регистрации программы для ЭВМ № 2021111121 «Программа математического моделирования оптимизации выбора температуры опорного наполнителя, физических свойств материала и структуры оболочковой формы по выплавляемым моделям для повышения ее трещиностойкости при охлаждении в ней отливки». Зарегистрировано в Реестре программ для ЭВМ 11.04.2021 г.

29. Евстигнеев А.И., Одиноков В.И., Дмитриев Э.А., Чернышова Д.В., Евстигнеева А.А., Иванкова Е.П. О трещиностойкости керамической оболочковой формы по выплавляемым моделям при затвердевании в ней шарообразной стальной отливки. Литейное производство. 2022;(9):22–25.

30. Одиноков В.И., Каплунов Б.Г., Песков А.В., Баков А.В. Математическое моделирование сложных технологических процессов. Москва: Наука; 2008:178.

Об авторах

В. И. Одиноков

Комсомольский-на-Амуре государственный университет
Россия

Валерий Иванович Одиноков, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью