Molecular dynamics study of the influence of carbon impurity on austenite nanoparticles crystallization during rapid cooling

Introduction

Metallic nanoparticles exhibit a unique set of physical, chemical, and optical properties. These properties make nanoparticles highly promising for applications in areas such as microelectronics, optoelectronics, plasmonics [1; 2], medicine and biology [3; 4], chemical catalysis, and the production of gas sensors [5; 6]. In the manufacturing of nanoparticles, significant attention is given to controlling the phase state, size, and shape of the particles due to their critical impact on beneficial properties [7 – 10]. Consequently, investigating the factors influencing the mechanisms and kinetics of phase transitions, as well as the final structure of the particles, is of great importance. Recently, particles with a high level of atomic structure disorder, such as amorphous or nanocrystalline structures, have garnered significant interest [11 – 14]. These particles possess high stored energy and a unique electronic structure, making them promising for use in catalysis, biomedicine, optics, and electronics [15 ‒ 17].

A nanocrystalline structure, which is a polycrystalline structure with relatively small grain sizes (ranging from a few nanometers to several tens of nanometers) and a high density of non-equilibrium grain boundaries, can be obtained not only through intense deformation but also through sufficiently rapid cooling, where the recrystallization process is suppressed during grain growth, leading to the formation of numerous small grains [18; 19]. Through computer modeling in studies [20 – 23], it has been shown, for example, that nanoparticles of pure metals crystallize with a nanocrystalline structure with high grain boundary density and an average grain size of only a few nanometers when cooled at a rate of approximately 10¹² K/s from the molten state. In studies [20; 22; 23], it was demonstrated that at a cooling rate exceeding 10¹³ K/s, homogeneous crystallization does not have time to occur, and the cooled particles in the molecular dynamics model exhibit an amorphous structure.

The interaction of impurity atoms of light elements with metals is of significant scientific and technological interest. Even at low concentrations, atoms of carbon, nitrogen, and oxygen significantly affect the properties of metals. Despite the importance of understanding the mechanisms and processes underlying the influence of alloying with light element impurities on the properties of metals, many questions regarding the behavior of impurities at the atomic level in the metallic matrix remain unresolved. One such question is the determination of the impact of impurities on phase transitions, particularly the exploration of ways to control the temperature intervals of phase existence in metallic nanomaterials by varying impurities. This study is devoted to investigating, at the atomic level using molecular dynamics, the crystallization process of austenite nanoparticles and the effect of carbon impurity on these processes.

Model description

For describing Fe – Fe interactions in austenite, the Lau EAM potential [24] was used, which accurately reproduces the structural, energetic, and elastic characteristics of austenite [24; 25]. To describe the interactions of iron atoms with carbon atoms and carbon atoms with each other in the metal matrix, Morse potentials [26] were used, determined based on experimental data on the dissolution energy and migration energy of carbon impurity atoms in the austenite crystal, atomic radii, their electronegativity, binding energy, and other characteristics.

In the model, a spherical austenite particle was initially created by cutting out a sphere of the appropriate size from an ideal FCC crystal. Particles with diameters ranging from 1.5 to 12.0 nm were considered. The particle was placed in a rectangular parallelepiped calculation cell with periodic boundary conditions. Although free conditions (i.e., the absence of any boundary conditions) can be used for this model, periodic boundary conditions were employed in this study to ensure that atoms evaporating from the particle surface at high temperatures do not escape far from the particle but remain within the calculation cell. The distance between the walls of the calculation cell was sufficiently large to prevent interaction between the particle and its virtual duplicate [27; 28].

Carbon impurity atoms were introduced randomly throughout the entire volume of the metallic particle. The impurity concentration varied from 0 to 10 at. %. After creating the initial spherical particle, structural relaxation was performed to establish the equilibrium atomic structure. Temperature control was carried out using the Nose-Hoover thermostat. The temperature in the model was set by adjusting the atomic velocities. The time integration step in the molecular dynamics method was 1 fs.

The resulting particles were used as starting points for simulating the gradual heating and subsequent cooling of the particles. For particles of each size, simulations were conducted with constant heating rates from the monocrystalline state to temperatures significantly exceeding the melting point (from 600 to 2000 K for larger particles and generally up to 1800 K for relatively small particles) and reverse cooling from the molten state to 600 K (for crystallization simulation). The temperature change during heating and cooling was carried out at a constant rate by correspondingly adjusting the velocity magnitudes of all atoms in the model. It is known that when cooling melts at rates above 10¹³ – 10¹⁴ K/s, homogeneous crystallization does not have time to occur even in pure metals, resulting in metallic glasses [29; 30]. At the same time, as shown in studies [20 – 23] and will be demonstrated below, cooling rate of 10¹² K/s is sufficient for crystallization to occur.

Results and discussion

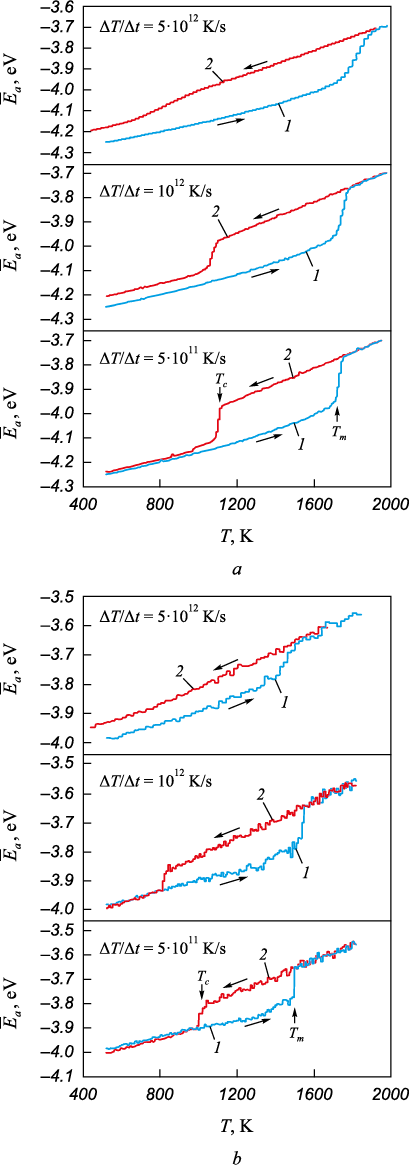
The average potential energy of an atom was chosen as the primary characteristic of the state of the nanoparticle structure. Fig. 1 shows the dependence of the average atomic energy on temperature for particles with diameters of 8.0 and 2.5 nm during heating from the monocrystalline state and reverse cooling from the melt at different temperature change rates: 5∙10¹¹, 10¹² and 5∙10¹² K/s. The sharp changes in the average atomic energy on the graphs apparently correspond to phase transitions: during the increase – melting, and during the decrease – crystallization. As is well known, the melting – crystallization phase transitions do not occur instantaneously; the crystal – liquid front moves at a finite speed, depending on the temperature, and usually ranges from several tens of meters per second [31; 32]. No stationary crystal – liquid front was observed; once formed, this front typically moved until the entire particle melted or crystallized. In light of the above, the phase transition temperatures were determined by the moment of their onset (indicated by arrows in Fig. 1).

Crystallization during gradual cooling from the melt occurred at a temperature significantly lower than the melting point. This substantial difference between the melting temperature (T_m) and the crystallization temperature (T_c) in nanoparticles is a well-known phenomenon in modeling [20; 22; 33]. As shown, the crystallization process is more sensitive to the rate of temperature change than melting: for all three rates, the onset of melting is roughly the same, while the crystallization onset temperatures vary considerably. At a cooling rate of 5·10¹² K/s, crystallization only partially occurred for the 8.0 nm particle (as indicated by the relatively small drop in average atomic energy) and did not occur at all for the 2.5 nm particle (Fig, 1, a). As is well known, homogeneous crystallization involves two stages: nucleation of crystalline nuclei followed by their growth, i.e., the advancement of the crystallization front. These stages occur sequentially, and once stable nuclei are formed, the front moves at approximately the same speed as during melting, as evidenced by the similar slopes of the graphs during melting and crystallization in most cases.

It should be noted that for the 8.0 nm particle, after crystallization, the average atomic energy is higher than in the initial monocrystalline particle (Fig. 1, a, curve 2), and the higher the cooling rate, the greater this difference. This is explained by the formation of a nanocrystalline structure after crystallization, characterized by higher average atomic energy values compared to the monocrystalline particle due to the presence of grain boundaries and other defects. The higher the cooling rate, the less time is spent on structural relaxation, and the higher the defect density in the cooled particle.

As the particle diameter decreased, the dependence of the average atomic energy on temperature underwent qualitative changes. Firstly, the energy difference between the crystalline and amorphous states was noticeably smaller compared to larger particles (Fig. 1, b). This is likely due to the relatively higher proportion of surface atoms in this case. Moreover, for smaller particles, the energy value fluctuations were higher, and the error in determining phase transition temperatures was greater, due to the relatively smaller number of atoms in them.

Another important change in the graphs with decreasing particle size was the decrease in melting and crystallization temperatures, as well as the stronger influence of the cooling rate on the crystallization temperature. This is obviously a consequence of the higher proportion of surface atoms as the particle diameter decreases. At a cooling rate of 5·10¹² K/s, crystallization did not occur at all for particles with diameters smaller than 3 nm, as evidenced by the absence of a downward energy jump corresponding to crystallization (e.g., Fig. 1, b, curve 2).

Fig. 2 shows the atomic structure in a cross-section of particles with an 8.0 nm diameter, obtained using a crystalline phase visualizer. This visualizer determines the affiliation of each atom to a particular crystalline structure by analyzing the arrangement of neighboring atoms [34]. As seen in Fig. 2, with increasing cooling rate, grain sizes decrease, and the number of structural imperfections, including grain boundaries, increases. At a cooling rate of 5·10¹¹ K/s, judging by the very close positioning of curves 1 and 2 in Fig. 1, i.e., the slight difference between the average energy of monocrystalline and crystallized particles, crystallization likely occurred often with the formation of low-energy grain boundaries (with a high density of coincident sites: special boundaries, twins).

To mathematically describe the influence of the free surface of nanoparticles on their melting temperature, a formula based on the assumption that the phase transition temperature change is proportional to the surface area-to-volume ratio of the particle is often used [35 – 37], i.e., for a spherical particle, this change should be proportional to N \(^{–1/3}\) or d \(^{–1}\) (where N is the number of atoms in the particle; d is the particle diameter). In this study, the assumption for the crystallization temperature was used, with an added correction δ accounting for the finite thickness of the particle’s surface layer:

where T_c and \(T_c^0\) are the crystallization temperatures of the particle and bulk material, respectively; α_c is a parameter that accounts for the extent of the particle surface’s influence on its crystallization.

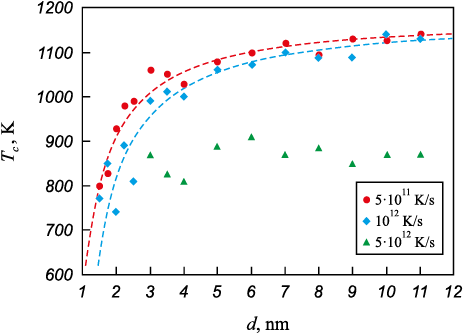
Formula (1) was used to construct an approximation curve for the dependence of the crystallization temperature of nanoparticles on their diameter (dashed lines in Fig. 3). As can be seen, for cooling rates of 10¹² K/s and 5·10¹¹ K/s, the values obtained in the model (shown by markers in Fig. 4) closely match the approximation curves, confirming the leading role of the free surface not only in the melting process but also in the crystallization of nanoparticles. The parameter values for calculation by formula (1) were as follows (1): \(T_c^0\) = 1190 K, α_c = 0.38 K·nm, δ = 0.4 nm for a cooling rate of 5·10¹¹ K/s and \(T_c^0\) = 1190 K, α_c = 0.49 K·nm, δ = 0.4 nm for a cooling rate of 10¹² K/s.

As shown in the dependencies in Fig. 3, the crystallization temperature increases as the cooling rate decreases. This fact confirms that the formation of nucleation sites is a probabilistic process requiring a relatively long time for the formation of stable nuclei. At a cooling rate of 5·10¹² K/s, particles with diameters smaller than 3 nm did not crystallize (triangular markers in Fig. 3). The error in determining the onset of crystallization at this rate was higher than at the other rates considered. Nevertheless, it is clear that at the highest of the rates considered, 5·10¹² K/s, crystallization occurs at lower temperatures than at lower rates.

The introduction of carbon impurity led to a decrease in the crystallization temperature. Fig. 4 shows the dependence of the crystallization temperature on particle diameter (Fig. 4, a) and carbon impurity concentration (Fig. 4, b). The following parameter values were obtained for calculation using formula (1): \(T_c^0\) = 1155 K, α_c = 0.57 K·nm for a concentration of 3 at. %; \(T_c^0\) = 1120 K, α_c = 0.59 K·nm for a concentration of 6 at. %. The δ value, which reflects the width of the surface layer, was found to be the same in all cases – 0.4 nm.

As the carbon concentration increased within the considered impurity atom concentration range, the crystallization temperature of the austenite particle decreased significantly: by nearly 200 K at a concentration of 10 at. % (Fig. 4, b). Carbon atoms, diffusing in the metal lattice, often formed clusters consisting of several carbon atoms (Fig. 5). These clusters distorted the emerging metal crystal lattice around them, hindering crystallization. Crystallization nuclei formed predominantly in the particle volume, followed by the intensive growth of crystals and the formation of a polycrystalline structure.

Fig. 5 shows the atomic structure of particles with a diameter of 8.0 nm, containing 3 at. % carbon, crystallized at different cooling rates. Comparing the structures shown in Fig. 2 for particles without carbon impurity, it is evident that the number of structural imperfections, grain boundaries, and other defects is significantly higher in the presence of carbon. The most notable difference was observed at the lowest cooling rate considered: 5·10¹¹ K/s. Without carbon impurity, the particle crystallized with a much lower defect density (Fig. 2, c) than in the presence of carbon (Fig. 5, c). In the latter case, the structure was almost indistinguishable from the structure obtained during cooling at a rate of 10¹² K/s (Fig. 5, b). Carbon impurity atoms, especially clusters of them, predominantly settled at grain boundaries and triple junctions.

Conclusions

A study using molecular dynamics was conducted to investigate the struc-tural formation during the crystallization of austenite nanoparticles in the presence of carbon impurity. The effects of melt cooling rate, particle size, and carbon atom concentration on the crystallization process, resulting structural features, and crystallization onset temperature were examined. It was shown that the formation of a nanocrystalline structure in nanoparticles can be controlled by varying the cooling rate and introducing carbon impurity. In the model used, at a cooling rate above 10¹³ K/s, crystallization did not occur; at a rate below 5·10¹² K/s, the austenite particles crystallized, forming a nanocrystalline structure. Additionally, as the cooling rate decreased, the defect density in the final structure also decreased. At a cooling rate of 5·10¹¹ K/s or less, crystallization of carbon-free particles resulted in the formation of low-energy grain boundaries (with a high density of coincident sites: special boundaries, twins).

The crystallization temperature at a cooling rate below 10¹² K/s is inverse-ly proportional to the particle diameter: as the particle size decreases, the proportion of the free surface increases, which reduces the probability of crystalline nuclei formation. Additionally, the crystallization temperature increases as the cooling rate decreases.

The introduction of carbon impurity led to a decrease in the crystallization temperature of nanoparticles: in the presence of 10 at. % carbon, the temperature decreased by approximately 200 K for particles of different sizes. Carbon atoms often formed clusters consisting of several atoms. These clusters distorted the forming metal crystal lattice around them, hindering crystallization. In the presence of carbon impurity, the final structure of the crystallized particles contained a higher density of grain boundaries and other defects. Carbon atoms, especially in clusters, predominantly settled at grain boundaries and triple junctions.