Математическое моделирование нагрева сляба в печи с шагающими балками с учетом их кривизны

Введение

Наиболее прогрессивными агрегатами, используемыми для нагрева слябов перед прокаткой в производстве горячекатаного листа, считаются печи с шагающими балками, в которых обеспечивается всесторонний подвод теплоты к поверхностям слябов [1]. Обычно такую схему подвода теплоты называют четырехсторонней, поскольку (что подтверждается опытом и расчетами) подвод теплоты к торцевым поверхностям слябов влияет на температурное поле лишь небольших участков слябов, прилегающих к этим поверхностям, а длина слябов в листопрокатном производстве во много раз больше их остальных размеров. Однако, несмотря на наличие нижней зоны обогрева в этих печах, условия подвода теплоты к верхней и нижней поверхностям нагреваемых слябов неодинаковы. Система транспортировки слябов содержит стационарные и подвижные балки, частично экранирующие от продуктов сгорания нижних зон обогрева, находящиеся с ними в контакте области нижней поверхности сляба, а также частично осуществляющие отвод теплоты к элементам системы охлаждения балок в местах контакта.

В результате на нижней поверхности слябов возникают «холодные пятна», влияние которых достигает не только внутренних горизонтальных сечений сляба, но и его верхней поверхности. Одним из способов уменьшения описанной неоднородности температурного поля является придание некоторой кривизны неподвижным балкам системы транспортировки, однако количественно этот эффект изучен недостаточно.

Экспериментальное исследование описанных выше факторов требует применения дорогостоящего современного оборудования [2] и в промышленных условиях затруднено. Поэтому оно используется обычно на этапах начала исследования (с целью получения первичной информации о его объекте) и его завершения (с целью проверки выработанных рекомендаций). Основная часть исследования осуществляется обычно путем математического моделирования процессов, происходящих в рабочем пространстве печи. Сравнение различных моделей нагрева металла в нагревательных печах [3] позволяет классифицировать их на статистические [4; 5], аналитические [6] и численные [7 – 10], причем в редких случаях рассматриваются не только прямые, но и обратные задачи теплопроводности [6; 11]. Математические модели печных процессов также широко применяются для решения оптимизационных задач [11 – 15] и используют возможности современных CFD-комплексов [16; 17].

В работе [18] предложена двумерная модель нагрева сляба в толкательной печи, отличительной особенностью которой является совместное решение задачи теплопроводности для нагреваемого сляба и участка опорной (глиссажной) трубы. Однако в этой модели труба направлена вдоль сляба, поэтому (с учетом двумерности модели) протяженность «холодного пятна» может отслеживаться только в направлении ширины сляба.

В работе [19] предложена трехмерная модель нагрева сляба в печи с переменными во времени граничными условиями, имитирующими прохождение слябом различных технологических зон проходной печи. Особенностью этой модели является возможность задания на нижней поверхности сляба кусочно-определенных граничных условий, различных для областей контакта этой поверхности с балками и открытых областей нижней поверхности сляба.

Целью настоящей работы является дальнейшее развитие математической модели нагрева сляба в печи с шагающими балками (с учетом воздействия этих балок на процесс нагрева) в направлении учета влияния возможной кривизны балок системы транспортировки на температурное поле сляба, и применение этой модели для проведения численных экспериментов.

Методы исследования

Разработанная модель представляет собой трехмерную задачу нестационарной теплопроводности в декартовой системе координат для расчетной области в форме параллелепипеда, без внутренних источников теплоты, с зависящими от температуры теплофизическими характеристиками и несимметричными переменными во времени граничными условиями третьего рода [19].

Эта дифференциальная задача не имеет аналитического решения, поэтому решать ее приходится численно, методом конечных разностей (методом баланса) [7; 19; 20].

Этот метод предполагает введение дискретного времени t_k = kΔt (k = 1, 2, ...) с постоянным шагом Δt и дискретных координат: x_i = iΔx (i = 0, 1, 2, ..., n_x); y_j = jΔy (j = 0, 1, 2, ..., n_y); z_l = lΔz (l = 0, 1, 2, ..., n_z), которые для данной простой геометрии также изменяются с постоянными шагами Δx, Δy и Δz. Значения n_x, n_y и n_z называют количеством разбиений заготовки вдоль каждого из координатных направлений.

В результате введения расчетной сетки вся расчетная область разбивается на элементарные объемы, количество которых равно (n_x + 1)(n_y + 1)(n_z + 1). Каждый из этих объемов содержит один узел пространственной сетки, которая задается трехиндексной нумерацией (i, j, l). На каждом шаге по времени для каждого элементарного объема записываются уравнения элементарного теплового баланса, образующие квазилинейную систему уравнений относительно узловых значений температуры в конце шага по времени. Решение ее общими методами (ввиду выраженной разреженности матрицы коэффициентов) нецелесообразно, в связи с чем более эффективными оказываются итерационные методы [19; 20], позволяющие отказаться от использования громадных вспомогательных матриц.

Выбор в модели граничных условий третьего рода обусловлен их стабилизирующим влиянием на сходимость итерационного алгоритма, применяемого при решении трехмерной задачи теплопроводности.

В соответствии с этими граничными условиями связь плотности теплового потока q_w на граничной поверхности (например, на верхней поверхности сляба) с ее температурой T_w описывается формулой Ньютона-Рихмана:

где T₀ – температура греющей среды, К; α – коэффициент теплоотдачи, Вт/(м²·К).

Учет теплового влияния балок системы транспортировки на тепловые условия на нижней поверхности сляба осуществляется путем разбиения нижней поверхности сляба на прямоугольные участки и задания различных граничных условий для этих участков. Данные прямоугольные участки применительно к рассматриваемой задаче могут быть трех типов:

– всегда открытые части поверхности;

– части поверхности, контактирующие с неподвижными балками;

– части поверхности, контактирующие с подвижными балками (в периоды подъема и перемещения сляба).

Для всегда открытых участков нижней поверхности граничные условия аналогичны условиям на верхней поверхности сляба (1), но с той лишь разницей, что могут отличаться сами значения температуры греющей среды и коэффициента теплоотдачи. Для остальных участков такое условие справедливо лишь в периоды отсутствия контакта с балками. Однако и в периоды контакта с балками для соответствующих участков также можно формально использовать выражение типа (1). В этом случае в качестве температуры среды должна фигурировать температура пароводяной смеси, циркулирующей в системе охлаждения балок, а в качестве коэффициента теплоотдачи – некоторый условный коэффициент теплопередачи k, Вт/(м²·К), от соответствующего участка нижней поверхности сляба к этой охлаждающей среде. Значение этого коэффициента зависит от конструкции системы транспортировки, и в данной модели является внешним (задаваемым) параметром [7; 19].

Цикл транспортировки сляба состоит из отдельных этапов (подъем сляба, перемещение вперед, опускание сляба, возврат подвижных балок в исходное положение), знание продолжительности которых (а также периода выдачи слябов из печи, периода раскладки слябов вдоль печи и хода штока системы транспортировки) позволяет в каждый момент времени задать граничные условия для каждой области нижней поверхности сляба. Однако такой подход требует производить расчет с шагом по времени не более 1 с, что может существенно увеличить продолжительность расчетной процедуры. В настоящей работе, как и в работе [19], применен более экономичный подход, позволяющий для каждой области контакта задавать средневзвешенные граничные условия типа (1), в которых фигурируют эффективный коэффициент теплоотдачи и эффективная температура среды. При этом вклад в эффективные значения характеристик отдельных периодов пропорционален их продолжительности.

В работе [19] разбиение нижней поверхности сляба на участки разного типа не меняется в процессе нагрева сляба, что соответствует прямым балкам. Особенностью настоящей работы является возможность задания кривизны балок путем представления их осевой линии в виде синусоиды, для которой задаются амплитуда (мм) и период (м). При задании значения амплитуды равным нулю балки считаются прямыми. При задании амплитуды (кривизны) отличной от нуля на каждом расчетном шаге по времени вычисляется продольная координата сляба относительно входного сечения печи, а затем для каждой балки (подвижной и неподвижной) рассчитывается отклонение границ пересечения со слябом относительно начального значения. Эта измененная область контакта сляба с балкой по-прежнему считается прямоугольной (ввиду относительной малости кривизны и ширины балки), но границы ее вдоль сляба смещаются, и уточнение этих границ в алгоритме, предлагаемом в настоящей работе, осуществляется на каждом расчетном шаге по времени.

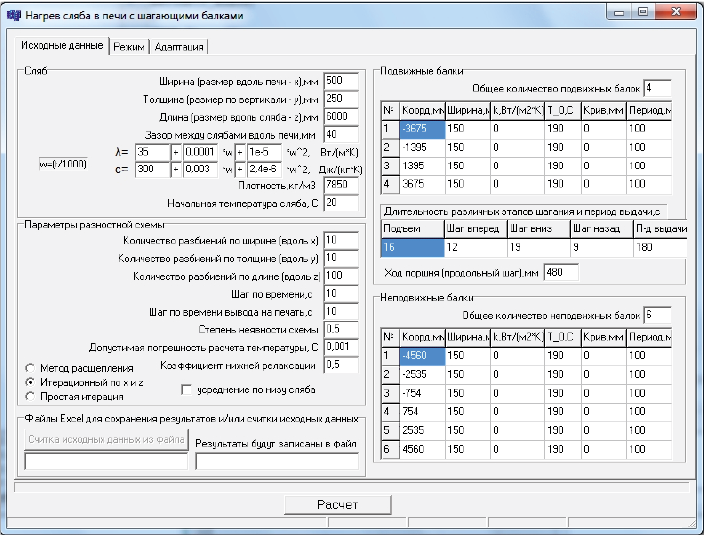
Программная реализация созданной математической модели осуществлена в визуальной среде разработки Builder C++ версии 6.0. На рис. 1 представлено стартовое окно расчетной программы, в котором для всех балок (помимо их положения, ширины, коэффициента теплопередачи к охлаждающей среде и температуры этой среды) могут быть заданы характеристики кривизны в форме амплитуды синусоиды и ее периода (значения по умолчанию, отображенные на рис. 1, соответствуют прямым балкам).

Во вкладке «Режим» (на рис. 1 она закрыта) задаются значения температуры греющей среды и коэффициентов теплоотдачи на каждой грани сляба по этапам нагрева, соответствующим технологическим зонам. Как уже отмечалось, эти значения для всех граней сляба используются непосредственно, а на нижней грани без изменений применяются только к открытым областям, в то время как для областей контакта с балками эти значения используются для вычисления эффективных коэффициентов теплоотдачи и эффективной температуры среды.

Результаты исследования

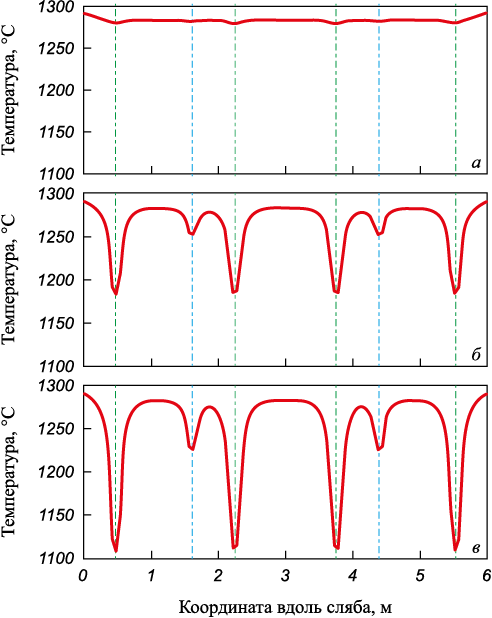
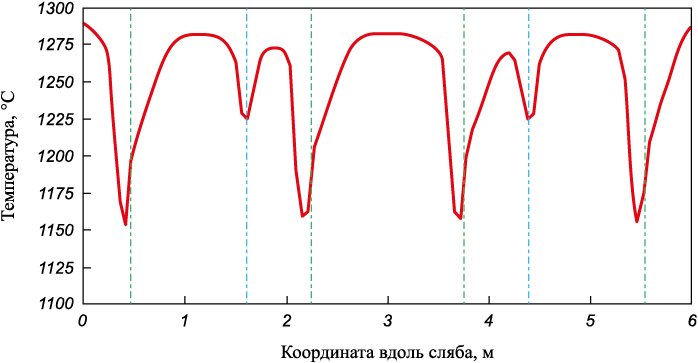
На рис. 2 представлено изменение температуры вдоль продольной оси нижней поверхности сляба с размерами 250×500×6000 мм, нагретого в печи, оснащенной четырьмя неподвижными (оси показаны зеленой линией) и двумя подвижными (оси показаны синей линией) балками. Результаты получены для трех значений интенсивности передачи теплоты балкам:

– k = 0 Вт/(м²·К), соответствует учету только экранирующего эффекта балок;

– k = 100 Вт/(м²·К), приближенно соответствует реальным конструкциям рейтеров;

– k = 50 Вт/(м²·К), соответствует промежуточным значениям.

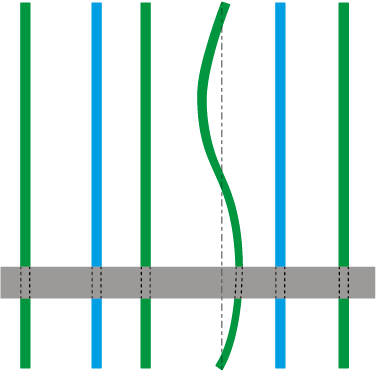
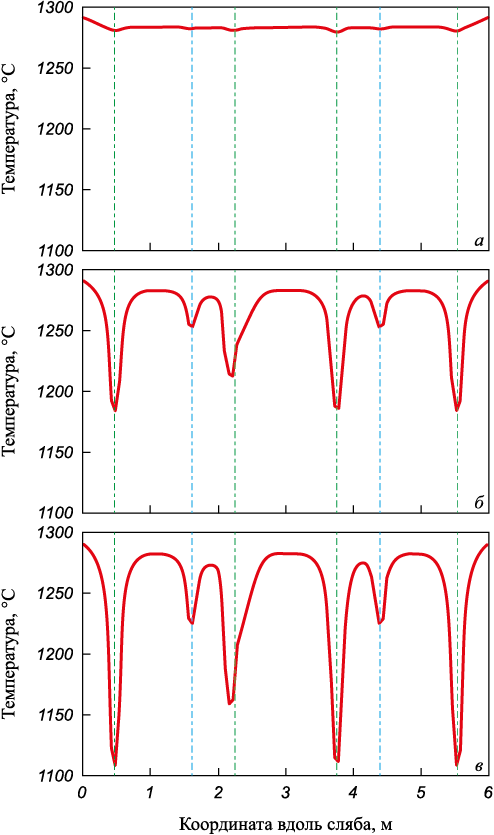
Для следующей серии расчетов моделировали искривление одной из неподвижных балок в соответствии с рис. 3. Искривление описали синусоидой с амплитудой 200 мм и периодом 5 м (параметры кривизны соответствовали предельно возможным на практике значениям). Результаты моделирования нагрева сляба при этих условиях представлены на рис. 4.

Если в случае нулевой интенсивности теплоотвода (рис. 4, а) влияние искривления балки практически незаметно, то при увеличении интенсивности теплоотвода к балкам возникает заметная асимметрия температурного профиля (рис. 4, б в сравнении с рис. 2, б и рис. 4, в в сравнении с рис. 2, в).

При этом общие характеристики нагрева останутся практически такими же, как и для нагрева с прямыми балками (см. таблицу). В представленной таблице колонки «минимум» и «максимум» содержат минимальные и максимальные значения температуры по всему объему сляба в конце цикла нагрева, колонка «перепад» – разность между ними, а колонка «средняя» – среднемассовую температуру сляба в конце нагрева.

На рис. 5 представлен температурный профиль вдоль продольной оси нижней поверхности сляба для случая искривления всех неподвижных балок.

Обсуждение результатов исследования

Как видно из полученных результатов, для неподвижных балок «пятно» воздействия глубже (т. е. «холоднее»), чем для подвижных балок. Это обусловлено тем, что при заданных значениях ширины сляба, периода выдачи и параметров механизма транспортировки время контакта участков нижней поверхности сляба с неподвижными балками больше, чем с подвижными.

Наличие теплоотвода от слябов к балкам создает гораздо большую неравномерность температуры нижней поверхности, чем просто экранирование ее от излучения продуктов сгорания нижних зон обогрева, как видно на рис. 2. Искривление одиночной балки может существенно изменить характеристику соответствующего «холодного» пятна, и этот эффект тем больше, чем сильнее теплоотвод к балкам (рис. 4, б, в). Однако он практически не влияет на общую характеристику неравномерности нагрева (см. таблицу), поскольку при искривлении балки площадь контакта с ней поверхности сляба не изменяется, а только «размазывается» во времени. Но если искривлению подвергнуть все неподвижные балки, то существенно сокращается итоговый перепад по слябу вследствие увеличения его минимальной температуры, что приводит к повышению однородности температурного поля сляба.

Выводы

Ранее разработанная и программно реализованная авторами математическая модель нагрева сляба в печи с шагающими балками, учитывающая воздействие этих балок на нижнюю поверхность сляба, модифицирована путем дополнения возможности учета кривизны балок.

Для печи, оснащенной четырьмя неподвижными и двумя подвижными балками, смоделирован нагрев сляба 250×500×6000 мм по штатному режиму при различной интенсивности теплоотвода к балкам для случаев прямых и искривленных балок.

Установлено, что интенсивность теплоотвода к балкам существенно влияет как на уровень температурного поля сляба, так и на его однородность.

В результате вариантных расчетов получено, что искривление только одной балки изменяет локальные характеристики соответствующего «холодного» пятна, практически не влияя на минимальные, максимальные и среднемассовые значения температуры сляба, а искривление всех балок (как минимум, одного типа) повышает минимальную температуру сляба и увеличивает однородность температурного поля сляба в целом. При этом влияние кривизны балок на температурное поле в конце нагрева (в частности, на его однородность) тем выше, чем интенсивнее теплоотвод к балкам.