Mathematical modeling of slab heating in a furnace with walking beams due to their curvature

Introduction

The furnaces with walking beams, which provide a comprehensive heat supply to the slab surfaces, are considered to be the most advanced units used for heating slabs before rolling in the hot-rolled sheet production [1]. Usually such a scheme of heat supply is called four-sided because (as confirmed by experience and calculations) heat supply to the end surfaces of slabs affects the temperature field of nothing but small sections of slabs adjacent to these surfaces, and the length of slabs in sheet rolling is many times greater than their other dimensions. However, although these furnaces have a lower heating zone, the conditions of heat supply to the upper and lower surfaces of the heated slabs are different. The slab transportation system includes fixed and movable beams, partially shielding the zones of the slab lower surface that are in contact with them from the combustion products of the lower heating zones, and also partially transferring heat to the elements of the beam cooling system in the places of contact.

As a result, “cold spots” emerge on the lower surface of slabs, the effect of which reaches out to the slabs upper surface, not only their inner horizontal sections. One of the ways to reduce the described inhomogeneity of the temperature field is to give some curvature to the fixed beams of the transportation system. However, no comprehensive quantity-related studies of this effect have been conducted.

Expensive modern equipment is required to explore the above-mentioned factors by experiment [2], which is not easy in industrial conditions. Therefore, an investigational study is usually conducted at the first stage of the research (to obtain primary information about the target of research) and at its last stage (to verify the recommendations made). The main part of the investigation is usually conducted by mathematical modeling of the processes occurring in the furnace working space. Different models of metal heating in the reheating furnaces [3] can be classified into statistical [4; 5], analytical [6] and numerical ones [7 – 10]. In rare cases, inverse heat conduction problems are addressed, along with direct ones [6; 11]. Optimization problems are also solved using mathematical models of furnace processes [11 – 15] that take advantage of modern CFD simulation software [16; 17].

The authors of [18] propose a two-dimensional model of slab heating in a pusher type furnace, the distinguishing feature of which is the joint solution of the heat conduction problem for the slab to be heated and for the section of the support tube (water-cooled skid). However, in this model, the tube is directed along the slab, so (given that the model is two-dimensional) the length of the “cold spot” can only be traced in the direction of the slab width.

The authors of [19] propose a three-dimensional model of slab heating in a furnace with time-varying boundary conditions simulating slab passage through different process zones of a pusher-type furnace. The peculiarity of this model is the possibility to set piecewise defined boundary conditions on the slab bottom surface, these conditions being different for the areas of this surface contact with beams and open areas of the slab bottom surface.

The purpose of this work is to further develop the mathematical model of slab heating in a furnace with walking beams (taking into account the impact of these beams on the heating process), considering the influence of the possible curvature of the transportation system beams on the slab temperature, and the use of this model for numerical experiments.

Research methods

The developed model is a three-dimensional trasient heat conduction problem in the Cartesian coordinate system for a parallelepiped-shaped computational domain without internal heat sources, with temperature-dependent thermophysical characteristics and asymmetric time-varying boundary conditions of the third kind [19].

This differential problem has no analytical solution; therefore, it has to be solved numerically, using the finite difference method (balance method) [7; 19; 20].

This method involves the introduction of discrete time t_k = kΔt (k = 1, 2, ...) with a constant step Δt and discrete coordinates: x_i = iΔx (i = 0, 1, 2, ..., n_x); y_j = jΔy (j = 0, 1, 2, ..., n_y); z_l = lΔz (l = 0, 1, 2, ..., n_z), which for this simple geometry also change with constant steps Δx, Δy and Δz. The values n_x, n_y and n_z are called the number of workpiece divisions along each of the coordinate directions.

As the computational grid is introduced, the entire calculation domain is divided into elementary volumes, the number of which is equal to (n_x + 1)(n_y + 1)(n_z + 1). Each of these volumes contains one node of the spatial grid determined by three indexes (i, j, l). At each time step, the elementary heat balance equations are recorded for each elementary volume, forming a quasi-linear system of equations with respect to the nodal temperature values at the end of the time step. The general solution methods are inadvisable in this case (due to the sparsity structure of the coefficient matrix), therefore iterative methods are more effective [19; 20], as they enable to discard huge auxiliary matrices.

We chose boundary conditions of the third kind in the model due to their stabilizing influence on the convergence of the iterative algorithm used for solving the three-dimensional heat conduction problem.

In accordance with these boundary conditions, the relationship between the heat flux density q_w on the boundary surface (e.g., on the slab top surface) and its temperature T_w is described by the Newton-Richman formula:

where T₀ is the temperature of the heating medium, K; α is the heat transfer coefficient, W/(m²·K).

The thermal influence of the transportation system beams on the thermal conditions on the slab bottom surface is taken into account by dividing the slab bottom surface into rectangular areas and setting different boundary conditions for these areas. These rectangular areas can be of three types with respect to the problem under consideration:

– always open parts of the surface;

– parts of the surface in contact with fixed beams;

– parts of the surface in contact with movable beams (when the slab is lifted or moved).

For always open areas of the lower surface, the boundary conditions are similar to those on the slab upper surface (1), the only difference is that the values of the heating medium temperature and heat transfer coefficient may not be the same. For the remaining areas, this condition is true only when there is no contact with the beams. However, during the periods of contact with the beams, an expression like (1) can also be formally used for the corresponding areas. In this case, the temperature of the steam-water mixture circulating in the beam cooling system should be used as the medium temperature, and some conditional coefficient of heat transfer k, W/(m²·K), from the corresponding area of the slab bottom surface to this cooling medium, should be used as the heat transfer coefficient. The value of this coefficient depends on the design of the transportation system, and it is an external (set) parameter in this model [7; 19].

The slab transportation cycle consists of separate stages (slab lifting, forward movement, slab lowering, movable beams return operations). When their duration is known (as well as the time for slab removal from the furnace, the time for putting slabs along the furnace and the transportation system valve rod travel), one can set the boundary conditions for each zone of the slab bottom surface at any given time. However, this approach requires calculation with a time step of no more than 1 s, which can significantly increase the duration of the calculation procedure. In the present work, as in [19], a more time-saving approach is applied, according to which, for each contact zone, weighted average boundary conditions of the type (1) are set, with the effective heat transfer coefficient and the effective temperature of the medium. At the same time, the contribution to the effective values of the individual periods characteristics is proportional to their duration.

In [19], the division of the slab bottom surface into areas of different types does not change during the slab heating process, which corresponds to straight beams. A special feature of the present work is that the curvature of beams can be set by representing their centerline as a sinusoid for which the amplitude (mm) and period (m) are set. When the amplitude value is set to zero, the beams are considered straight. When the amplitude (curvature) is set different from zero, the slab longitudinal coordinate relative to the furnace entrance section is calculated at each time step, and then the deviation of the boundaries of intersection with the slab relative to the initial value is calculated for each beam (movable and fixed). This modified slab-beam contact zone is still considered rectangular (due to the relatively small curvature and width of the beam), but its boundaries along the slab are shifted, and the algorithm proposed in this paper adjusts these boundaries at each computational time step.

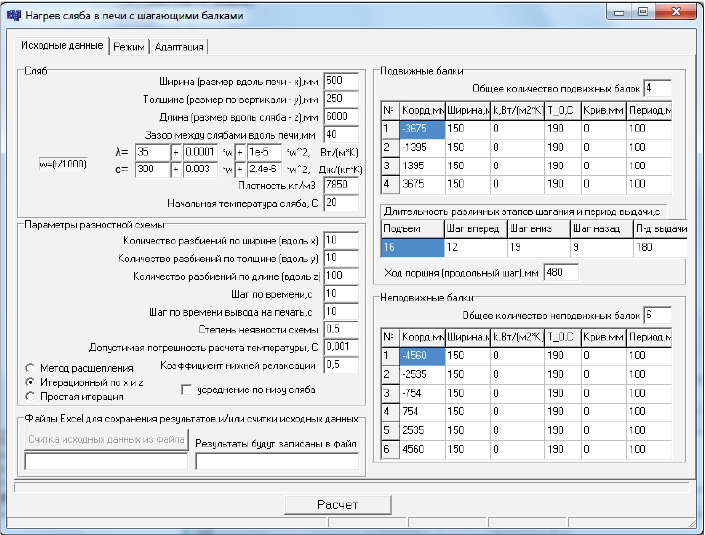
The created mathematical model is implemented in the visual development environment Builder C++ version 6.0. Fig. 1 shows the start window of the calculation program, in which the curvature characteristics in the form of sinusoid amplitude and its period (default values shown in Fig. 1 correspond to straight beams) can be set for all beams (in addition to their position, width, coefficient of heat transfer to the cooling medium and temperature of this medium).

In the “Mode” tab (in Fig. 1 it is closed), the values of the heating medium temperature and heat transfer coefficients on each slab face by heating stages are set for the corresponding technological zones. As mentioned above, these values for all slab faces are used directly, and at the bottom face, they are applied unchanged to the open zones only, while for the beam contact zones, these values are used to calculate the effective heat transfer coefficients and the effective medium temperature.

Research results

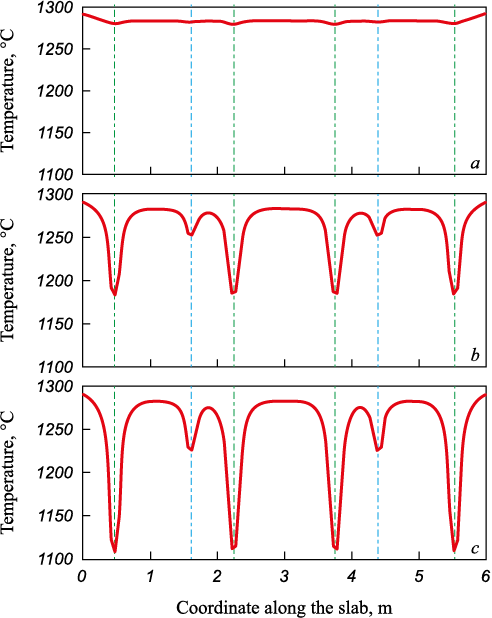
Fig. 2 shows the temperature variation along the longitudinal axis of the slab bottom surface, with dimensions 250×500×6000 mm, heated in a furnace equipped with four fixed (axes are indicated by a green line) and two movable (axes are indicated by a blue line) beams. The results are obtained for three values of intensity of heat transfer to the beams:

– k = 0 W/(m²·K), corresponds to the case when the shielding effect of beams only is taken into account;

– k = 100 W/(m²·K), approximately corresponds to the actual rider designs;

– k = 50 W/(m²·K), corresponds to intermediate values.

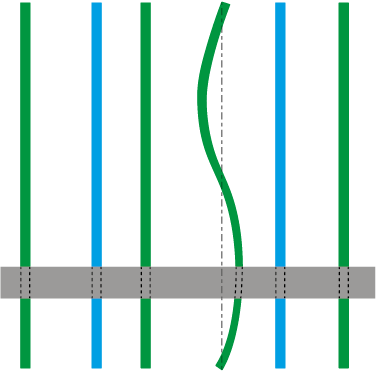
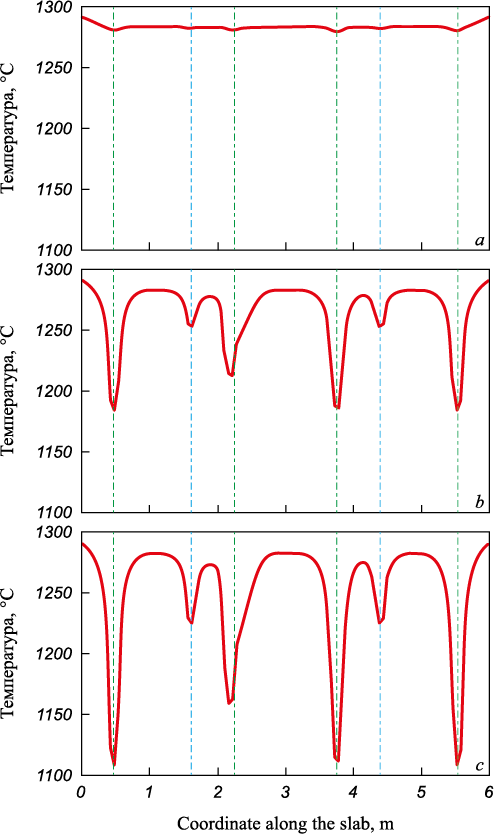
For the next series of calculations, the curvature of one of the fixed beams was modeled according to Fig. 3. The curvature was described by a sinusoid with an amplitude of 200 mm and a period of 5 m (the curvature parameters corresponded to the maximum practically feasible values). Fig. 4 shows the results of slab heating simulation under these conditions.

In the case of zero heat transfer intensity (Fig. 4, а), the influence of beam curvature is practically imperceptible. However, as the intensity of heat transfer to the beams increases, the temperature profile becomes noticeably asymmetrical (Fig. 4, b compared to Fig. 2, b and Fig. 4, c compared to Fig. 2, c).

At the same time, the overall heating characteristics will remain essentially the same as for heating straight beams (see the Table). In the Table, the “minimum” and “maximum” columns contain the minimum and maximum temperature values throughout the slab at the end of the heating cycle, the “difference” column presents the difference between them, and the “average” column indicates the slab bulk temperature at the end of the heating cycle.

Fig. 5 shows the temperature profile along the longitudinal axis of the slab bottom surface for the case when all fixed beams are curved.

Discussion of the research results

The results obtained revealed that for fixed beams the “spot” of impact is deeper (i.е. “cooler”) than for movable beams. This is because at given values of the slab width, removal period and transportation mechanism parameters, the contact time of slab bottom surface areas with fixed beams is longer than with movable beams.

Fig. 2 shows that when heat is transferred from the slabs to the beams, the lower surface temperature is much more inhomogeneous than when this surface is just shielded from the radiation of the lower heating zones combustion products. The curvature of a single beam can significantly change the characteristic of the corresponding “cold” spot, and this effect enhances as the heat transfer to the beams increases (Fig. 4, b, c). However, it has little or no effect on the general characteristic of the slab heating non-uniformity (see the Table), as when the beam curves, the slab surface contact area does not change, but only takes more time. However, if all fixed beams are subjected to curvature, the final difference across the slab is significantly reduced due to an increase in its minimum temperature, which leads to enhanced homogeneity of the slab temperature field.

Conclusions

The mathematical model of slab heating in a furnace with walking beams, earlier developed and programmatically implemented by the authors, that took into account the impact of these beams on the slab bottom surface, was modified by adding the possibility of considering the curvature of the beams.

We simulated heating of a 250×500×6000 mm slab for a furnace equipped with four fixed and two movable beams under standard mode with different intensity of heat transfer to the beams (the beams being straight or curved).

It is found that the intensity of heat transfer to the beams significantly affects both the level of the slab temperature field and its homogeneity.

The variant calculations showed that the curvature of only one beam changes the local characteristics of the corresponding “cold” spot, practically not affecting the minimum, maximum and bulk values of the slab temperature, while the curvature of all beams (of at least one type) increases the minimum slab temperature and homogeneity of the slab temperature field as a whole. Moreover, the more intensive the heat transfer to the beams is, the higher the impact of the beam curvature on the temperature field at the end of heating (in particular, on its homogeneity).