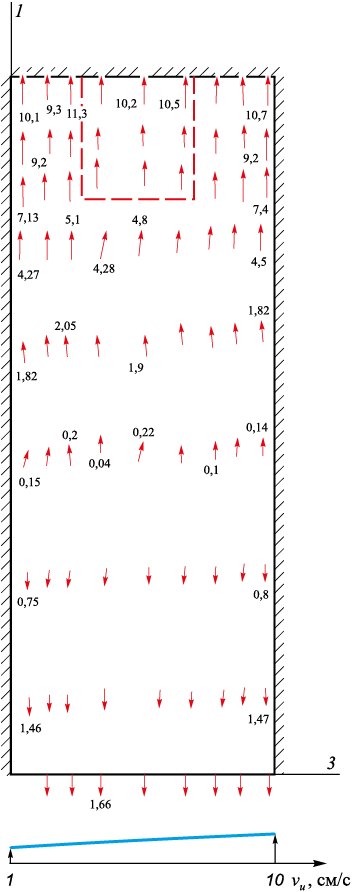Перейти к:
Моделирование нового процесса перемешивания жидкого металла в кристаллизаторе установки непрерывной разливки стали при вращающейся рубашке с вертикальными ребрами
https://doi.org/10.17073/0368-0797-2023-6-733-742
Аннотация
Предложена новая технология процесса заполнения кристаллизатора установки непрерывной разливки стали (УНРС) жидким металлом и его перемешивания. Приведена оригинальная запатентованная конструкция устройства, состоящая из глуходонного стакана и вращающейся рубашки. Экспериментальные исследования течения жидкого металла в кристаллизаторе продолжительны, сложны и трудоемки, поэтому в работе применяется математическое моделирование численным методом. Представлены основные результаты исследований течения расплава в объеме кристаллизатора. Объектами исследований являются гидродинамические и тепловые потоки жидкого металла нового процесса разливки стали в кристаллизатор прямоугольного сечения УНРС, а результатом – пространственная математическая модель, описывающая потоки и температуры жидкого металла в кристаллизаторе. Для моделирования процессов, протекающих при течении металла в кристаллизаторе, авторы используют специально созданный программный комплекс. В основе теоретических расчетов лежат основополагающие уравнения гидродинамики, уравнения математической физики (уравнение теплопроводности с учетом массопереноса) и апробированный численный метод. Исследуемая область разбивается на элементы конечных размеров, для каждого элемента в разностном виде формулируется система уравнений. Результат решения – поля скоростей и температур потока металла в объеме кристаллизатора. По разработанным численным схемам и алгоритмам составлена программа расчета. Приведен пример расчета разливки стали в кристаллизатор прямоугольного сечения, схемы потоков жидкого металла по различным сечениям кристаллизатора. Наглядно представлены векторные потоки жидкого металла в различных сечениях кристаллизатора при разных числах оборотов вращающейся рубашки. Выявлены области интенсивной турбулентности. Результаты численного решения задачи представлены в графической форме схемами полей скоростей потоков жидкого металла и их температуры по различным сечениям кристаллизатора.
Ключевые слова
Для цитирования:
Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Карпенко В.А. Моделирование нового процесса перемешивания жидкого металла в кристаллизаторе установки непрерывной разливки стали при вращающейся рубашке с вертикальными ребрами. Известия высших учебных заведений. Черная Металлургия. 2023;66(6):733-742. https://doi.org/10.17073/0368-0797-2023-6-733-742
For citation:
Odinokov V.I., Evstigneev A.I., Dmitriev E.A., Karpenko V.A. Simulation of a new process of mixing liquid metal in CCM mold with rotating cooling jacket with vertical ribs. Izvestiya. Ferrous Metallurgy. 2023;66(6):733-742. https://doi.org/10.17073/0368-0797-2023-6-733-742
Введение
Все больший интерес среди исследователей и производственников проявляется к разработке новых и совершенствованию существующих способов подачи и перемешивания жидкого металла в кристаллизаторе УНРС и МНЛЗ, а также устройств для их осуществления.
Экспериментальные исследования течения жидкого металла в кристаллизаторе являются продолжительным, сложным и трудоемким процессом, поэтому все шире используется для этого математическое моделирование, особенно численными методами.
Теоретические и практические вопросы подачи и перемешивания жидкого металла в кристаллизаторе УНРС рассмотрены в многочисленных работах отечественных и зарубежных исследователей, в том числе и по изучению качества получаемых заготовок.
Известен традиционный способ [1 – 5] создания условий для более равномерного омывания жидким металлом стенок кристаллизатора и получения однородной структуры по периметру заготовки, когда металл из промежуточного ковша поступает в кристаллизатор через окна глуходонного погружного стакана, расположенные друг относительно друга под углом 180°.
Предложен ряд новых способов выхода жидкого металла в кристаллизатор из погружного стакана: различные наклоны окон [6], их эксцентричное расположение [7], установка нескольких погружных стаканов [8], электромагнитное перемешивание жидкого металла в кристаллизаторе [9], выход металла на отражатель [10].
Другие новаторские решения и практические результаты по подаче жидкого металла в кристаллизатор УНРС и его перемешивание представлены в работах [11 – 13].
Продолжаются разработки моделей для математического исследования процессов течения жидкого металла в кристаллизаторе и затвердевания стали, а именно, за счет применения цифрового моделирования [14], установления важности вторичного потока при вращательном электромагнитном перемешивании стали при непрерывной разливке [15], моделирования течения металла внутри МНЛЗ и УНРС [16; 17], турбулентного течения и переноса частиц при непрерывной разливке стали [18], а также моделей затвердевания металла [19 – 21] и теплопередачи при затвердевании [22 – 24].
При этом для ряда способов подачи жидкого металла в кристаллизатор уже построены математические модели, позволяющие по движущемуся жидкому металлу в объеме кристаллизатора оценить эффективность того или иного устройства, с помощью которого осуществляется рассматриваемый процесс [7; 8].
Однако очень мало работ посвящено математическому моделированию этих процессов (особенно численными методами), что ограничивает возможности проектирования новых технологий подачи и перемешивания жидкого металла в УНРС и МНЛЗ.
Несмотря на имеющийся задел и опыт, следует отметить, что проблема проектирования и моделирования процессов и устройств подачи и перемешивания расплава в кристаллизаторе изучено недостаточно широко, что подчеркивает актуальность решаемых задач.
Таким образом, актуальной задачей остается разработка новых процессов по подаче и перемешиванию расплава в кристаллизаторе и их математическое моделирование, позволяющее еще на стадии разработки и проектирования новых устройств предсказать их работоспособность и эффективность.
В настоящей работе предложены новые технологии разливки жидкого металла в кристаллизатор за счет использования эффекта вращения для перемешивания в кристаллизаторе.
Целью настоящей работы является построение математической модели, описывающей гидродинамические процессы в кристаллизаторе УНРС при использовании нового предложенного способа подвода стали в кристаллизатор, а также обоснование полезности применения принудительного вращения для подачи и перемешивания жидкого металла в кристаллизаторе установки непрерывной разливки стали по сравнению со свободным вращением стакана при разливке стали.
В настоящей работе описывается и анализируется новый процесс подачи и перемешивания жидкой стали в кристаллизаторе УНРС [25]. Рассматриваемый процесс, в отличие от описанных ранее [26; 27], позволяет в широких диапазонах регулировать скорость перемешивания жидкого металла в кристаллизаторе УНРС, что способствует получению более качественного непрерывного слитка.
На рис. 1 изображена схема этого устройства. Из ковша 1 металл через глуходонный стакан 2 поступает в кристаллизатор 5. Глуходонный стакан 2 имеет эксцентрично расположенные отверстия 4. По наружной поверхности глуходонного стакана выше его выходных отверстий установлена с зазором огнеупорная рубашка 3, имеющая ребра 6. Рубашка соединена с механизмом вращения, состоящим из упорного подшипника 7, редуктора 8 и электродвигателя 9.
Рис. 1. Схема устройства для подачи и перемешивания стали |
Рассматриваемый процесс не стационарный (квазистационарный). При математическом описании процесса были приняты допущения (формализация). Глуходонный стакан в сечении выпуска и вращающаяся огнеупорная рубашка имеют одинаковое внешнее квадратное сечение, поэтому огнеупорная рубашка при вращении будет перемешивать жидкий металл в кристаллизаторе также и своими гранями.
При заданном направлении вращения одна половина грани квадрата огнеупорной рубашки как бы выталкивает жидкий металл от себя, а вторая ‒ его втягивает. В этом случае можно считать погружной стакан неподвижным, а через грани рубашки втекает и вытекает металл со скоростями, пропорциональными скоростям вращения и геометрическим размерам квадратного сечения этой огнеупорной рубашки. Такая идеализация подробно описана в работе [1] и позволяет рассматривать данный процесс как стационарный. Кроме того, не учитывают появляющуюся на гранях кристаллизатора корочку затвердевшего металла.
Среда (жидкий металл) считается несжимаемой. Рассмотрим уравнения гидродинамики. Для течения ньютоновской вязкой несжимаемой жидкости справедливы следующие уравнения (процесс стационарный):
| \[{\sigma _{ij,j}} + F_i^* = I_i^*;{\rm{ }}I_i^* = \rho \left( {{{\dot v}_i} + {v_k}\frac{{\partial {v_i}}}{{\partial {x_k}}}} \right);\] | (1) |
| \[{\sigma _{ij}} - \sigma {\delta _{ij}} = 2\mu {\xi _{ij}};{\rm{ }}{\xi _{ij}} = \frac{1}{2}\left( {{v_{i,j}} + {v_{j,i}}} \right);\] | (2) |
| vi, i = 0; i = 1, 2, 3; | (3) |
| \[\frac{{d\theta }}{{d\tau }} = a\Delta \theta ;{\rm{ }}\frac{{d\theta }}{{d\tau }} = {v_i}\frac{{\partial \theta }}{{\partial {x_i}}};{\rm{ }}i = 1,{\rm{ }}2,{\rm{ }}3,\] | (4) |
здесь σij – компоненты тензора напряжений; ξij – компоненты тензора скоростей деформаций; δij – символ Кронекера; p – давление в данной точке (p = –σ); σ – гидростатическое напряжение; μ – коэффициент вязкости, (г·с)/см2; vi – проекция скоростей перемещений по координатным осям xi (i = 1, 2, 3); ρ – плотность жидкого металла; \(F_i^*\) – проекция удельной объемной силы на координатные оси xi (i = 1, 2, 3); τ – время; Δ – оператор Лапласа; θ – температура; a = λ/(cγ) – температуропроводность; λ – коэффициент теплопроводности; c – удельная теплоемкость; γ – плотность (все они принимаются постоянными (константами)).
Для стационарного процесса:
\[{\dot v_i} = \frac{{\partial {v_i}}}{{\partial \tau }} = 0.\]
Уравнение теплопроводности записано с учетом массопереноса и стационарности.
На рис. 2 представлена расчетная схема рассматриваемого процесса.
Граничные условия задачи следующие (рис. 2):
| \[\begin{array}{c}{\left. {{\sigma _{11}}} \right|_{{\Gamma _2}}} = {p_1};{\left. {{\rm{ (}}{\sigma _{12}} = {\sigma _{13}})} \right|_{{\Gamma _i}}} = 0;{\rm{ }}i = 1 \div 3;\\{\left. {{\rm{(}}{\sigma _{21}} = {\sigma _{23}})} \right|_{{\Gamma _i}}} = 0;{\rm{ }}i = 5 \div 8;\\{\left. {{\rm{(}}{\sigma _{31}} = {\sigma _{32}})} \right|_{{\Gamma _i}}} = 0;{\rm{ }}i = 9 \div 11;\\{\left. {{\rm{(}}{\sigma _{21}} = {\sigma _{23}})} \right|_{{{\Gamma '}_{\rm{8}}}}} = 0;{\rm{ }}{\left. {{\rm{(}}{\sigma _{31}} = {\sigma _{32}})} \right|_{{{\Gamma '''}_{\rm{8}}}}} = 0;\\{\left. {{v_2}} \right|_{{\Gamma _5}}} = {v^*};\\{\left. {{v_3}} \right|_{{{\Gamma ''}_{\rm{8}}}}} = {V_t};\\{\left. {{v_2}} \right|_{{{\Gamma '}_{\rm{8}}}}} = {V_t};\\{\left. {{v_1}} \right|_{{\Gamma _{\rm{1}}}}} = {v_u};\\{\left. {{v_1}} \right|_{{\Gamma _{\rm{3}}}}} = 0;\\{\left. {{v_2}} \right|_{{\Gamma _i}}} = 0;{\rm{ }}i = 6 \div 8;\\{\left. {{v_3}} \right|_{{\Gamma _i}}} = 0;{\rm{ }}i = 9 \div 11.\end{array}\] | (5) |
При решении уравнения теплопроводности (4) использовались граничные условия:
| \[\begin{array}{c}{\left. \theta \right|_{{\Gamma _i}}} = \theta _i^*;{\rm{ }}i = 1 \div 10;\\{\left. q \right|_{{\Gamma _i}}} = q_i^*;{\rm{ }}i = 6,{\rm{ }}7,{\rm{ }}9,{\rm{ }}10.\end{array}\] | (6) |
здесь vu – скорость вытягивания слитка (рис. 2); \(v_2^*\) ‒ скорость выхода жидкого металла из окон погружного стакана; \(\theta _i^*\) ‒ заданные функции распределения температуры металла на поверхностях Гi ; \(q_i^*\) ‒ заданные из экспериментальных данных тепловые потоки через поверхности Гi ; \(\theta _5^*\) ‒ заданная температура выхода металла из окна Г5 .
Численная схема и алгоритм решения системы уравнений (1) ‒ (4) при граничных условиях (5), (6) подробно описаны в работе [28] с использованием широко апробированного численного метода.
Ниже приводятся результаты полученного численного решения поставленной задачи в различных сечениях кристаллизатора с их анализом.
Результаты численного расчета
Принимаем следующие существующие размеры кристаллизатора: Н = 100 см; В = 12,5 см; l = 100 см; h = 20 см; b = 7,5 см; δh = 8,5 см; δB = 1,5 см; δ1 = 1,5 см; vu = 1 м/мин = 1,66 см/с. Для стационарного процесса величину v\(^{*}\) определяли из равенства секундных объемов:
\[{v_u}Bl = {v^*}{\delta _n}{\delta _B} \Rightarrow {v^*} = \frac{{{v_u}Bl}}{{{\delta _n}{\delta _B}}}.\]
Температура истекания жидкой стали из окна (Г5 ) принимали \({\left. {{\theta ^*}} \right|_{{\Gamma _5}}}\) = 1600 °С. Температуры на поверхностях стакана (рис. 2) Гi (i = 3, 8, 8′, 11) принимались по экспериментальным данным \({\left. {{\theta ^*}} \right|_{{\Gamma _i}}}\) = 1550 °С, i = 3, 8, 8′, 11. На поверхности Г2 (рис. 2) находится жидкая шлаковая «рубашка», температура которой \({\left. {{\theta ^*}} \right|_{{\Gamma _2}}}\) = 1550 °С.
Рис. 2. Формализованная расчетная схема процесса разливки металла в кристаллизатор |
Константы λ = 0,29 Вт/(см·с); c = 444,47 Дж/(кг·с); γ = 7,8 г/см3. Коэффициент вязкости μ = 2,1·10\(^–\)4 (кг·с)/м2 в уравнениях (2) принимался по работе [29].
На рис. 3 показаны потоки металла в сечении А ‒ А при вращении рубашки со скоростью (n) 30 и 50 об/мин. Картины течения схожие, но более интенсивно при n = 50 об/мин (рис. 3, б). В сечении А ‒ А имеет место хаотичное движение металла в области погружного стакана. Звездочками на рис. 3, б помечены области, где температура металла выше температуры кристаллизации. В сечении А ‒ А отслеживается более выраженная неравномерность температур в потоках движущегося металла.
Рис. 3. Поле скоростей потоков течения металла в кристаллизаторе в сечении А ‒ А |
На рис. 4 показаны потоки металла в сечении В ‒ В – это вертикальное сечение у выхода металла из погружного стакана. На рис. 4 показаны потоки при вращении рубашки при n, равном 30 и 50 об/мин. Все векторы потоков направлены преимущественно вниз. Интенсивность, как и следовало ожидать, больше при n = 50 об/мин.
Рис. 4. Поле скоростей потоков течения металла в кристаллизаторе в сечении В ‒ В |
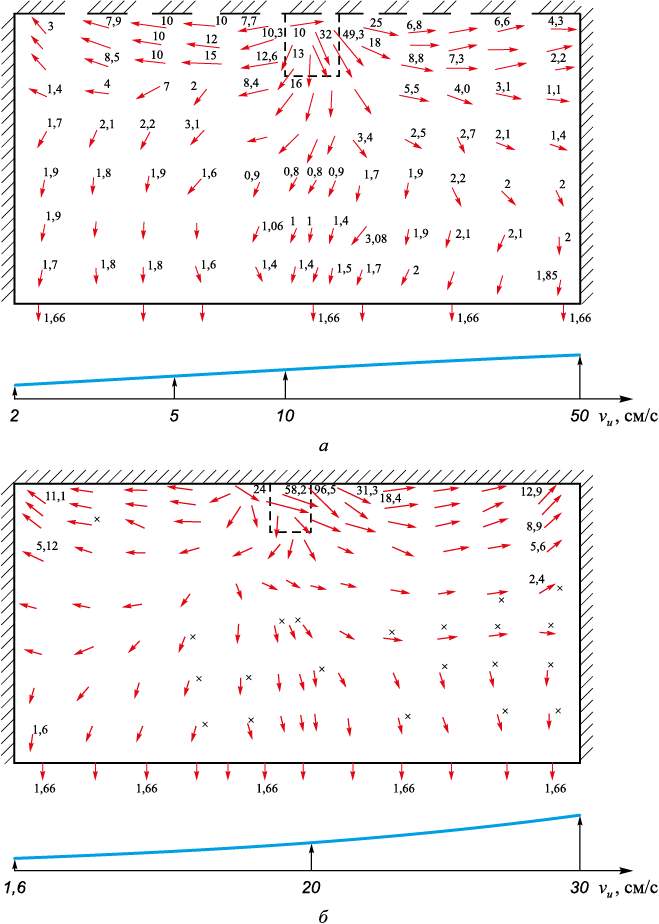
На рис. 5, а изображены потоки металла в сечении D ‒ D (рис. 2) при вращении рубашки при n, равном 30 и 50 об/мин. Наблюдаются малые вихри под погружным стаканом по его центру при n = 30 об/мин (рис. 5, а), при n = 50 об/мин – вихри отсутствуют. Скорость потока металла по боковым граням значительно выше, чем под погружным стаканом.
Рис. 5. Поле скоростей потоков течения металла в кристаллизаторе в сечении D ‒ D |
На рис. 6 показаны векторные потоки металла в горизонтальном сечении Е ‒ Е при скорости вращения рубашки n, равном 30 и 50 об/мин.
Рис. 6. Поле скоростей потоков течения металла в кристаллизаторе в сечении Е ‒ Е |
Векторные потоки мало чем отличаются как по характеру движения, так и по скорости. Для величины n = 50 об/мин на рис. 7 приведены потоки металла в горизонтальном сечении погружного стакана по выходным окнам (сечение Ж ‒ Ж). Наблюдаем тот же характер течения металла, что и в сечении Е ‒ Е (рис. 6), но более интенсивной величины.
Рис. 7. Поле скоростей потоков течения металла в кристаллизаторе в сечении Ж ‒ Ж |
При скорости вращения n = 50 об/мин металл в узких стенках кристаллизатора может проникать в область шлаковой подушки. На рис. 8 показано поле движения жидкого металла (сечение Г′ ‒ Г′). Действительно, движение жидкого металла направлено вверх, причем это движение охватывает по высоте половину вертикальной плоскости боковой стенки кристаллизатора, ускоряясь к шлаковой рубашке, где достигает 10 см/с. В сечении D ‒ D металл устремляется интенсивно вниз от шлаковой рубашки (рис. 5, б). Можно предположить, что под шлаковой рубашкой происходит интенсивные вихревые движения металла. Это не очень полезное явление, так как может быть захват шлака в область непрерывного слитка, что негативно повлияет на его качество.
Рис. 8. Поле скоростей потоков течения металла в кристаллизаторе в сечении Г′ ‒ Г′ |
Выводы
Получены численные результаты теоретического исследования:
‒ при принудительном перемешивании жидкого металла в кристаллизаторе прямоугольного сечения происходит интенсивное омывание стенок кристаллизатора, что безусловно способствует отводу тепла от жидкого металла к стенкам кристаллизатора;
‒ внутри кристаллизатора, особенно в верхней его части наблюдается ускоренное движение потоков жидкого металла;
‒ на узких стенках кристаллизатора наблюдается заброс жидкого металла (даже при n = 30 об/мин) в область шлаковой рубашки, что может привести к попаданию части шлака в непрерывно-литой слиток; чтобы избежать этого явления, можно продвинуть погружной стакан вместе с вращающейся рубашкой глубже в кристаллизатор, что возможно при увеличении высоты кристаллизатора.
Список литературы
1. Дюдкин Д.А., Кисиленко В.В., Смирнов А.Н. Производство стали. Т. 4. Непрерывная разливка металла. Москва: Теплотехник; 2009:528.
2. Ефимов В.А. Разливка и кристаллизация стали. Москва: Металлургия; 1976:552.
3. Акименко А.Д., Гирский В.Е., Гуськов А.И. Влияние способов подвода металла в кристаллизатор на формирование осевой зоны квадратного слитка. Сталь. 1973;(5):408–409.
4. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И. Численное моделирование процесса заполнения металлом кристаллизатора УНРС*. Известия вузов. Черная металлургия. 2017;60(6):493–498. https://doi.org/10.17073/0368-0797-2017-6-493-499
5. Proceedings of the Int. Symp. on Electromagnetic Processing of Materials. October 25–28, 1994. Nagoya, Japan: ISIJ; 1994:580.
6. Стулов В.В., Матысик В.А., Новиков Т.В., Щербаков С.В., Чистяков И.В., Плотников А.П. Разработка нового способа разливки слябовых заготовок на МЛНЗ. Владивосток: Дальнаука; 2008:156.
7. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И. Математическое моделирование процесса течения металла в кристаллизаторе при его подаче из погружного стакана с эксцентричными отверстиями. Известия вузов. Черная металлургия. 2018;61(8):606–612. https://doi.org/10.17073/0368-0797-2018-8-606-612
8. Куберский С.В., Семирягин С.О., Федоров О.В. Расчеты технологических и конструктивных параметров МЛНЗ: Учебное пособие. Алчевск: ДОНГТУ; 2006:146.
9. Смирнов А.А., Нисковских В.М., Куликов В.И. Исследование процесса электромагнитного перемешивания металла в слябовых МНЛЗ методом моделирования. В кн.: Совершенствование конструкций, исследование и расчет машин непрерывного литья заготовок: Сборник научных трудов. Москва: ВНИИМЕТМАШ; 1987:85–90.
10. Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А. Численное моделирование процесса заполнения металла кристаллизатора с отражателем УНРС. Известия вузов. Черная металлургия. 2019;62(10):747–755. https://doi.org/10.17073/0368-0797-2019-10-747-755
11. Нарцт Х.-П., Келлерер С., Штахельбергер К., Мёрвальд К., Федершпиль К., Валь Г. Новаторские решения и практические результаты технологии непрерывного литья слябов. Черные металлы. 2003;(11):34–38.
12. Виммер Ф., Тене X., Пекштайнер Л. Высокоскоростное литье мелкосортовых заготовок на МНЛЗ с кристаллизатором «Дайэмоулд». Сталь. 1999;(6):22–26.
13. Айхингер А., Фрауэнхубер К., Хедль X., Мервальд К. Новейшее оборудование для высокопроизводительной непрерывной разливки. Сталь. 2000;(3):25–28.
14. Олер К., Оденталь Х.-Ю., Пфайфер Г., Леманович И. Цифровое моделирование процессов течения и затвердевания металла в МНЛЗ для литья тонких слябов. Черные металлы. 2002;(8):22–30.
15. Davidson P.A., Boysan F. The importance of secondary flow in the rotary electromagnetic stirring of steel during continuous casting. Applied Scientific Research. 1987;44(1–2):241–259. http://doi.org/10.1007/BF00412016
16. Thomas B.G., Mika L.J., Najjar F.M. Simulation of fluid flow inside a continuous slab casting machine. Metallurgical Transactions B. 1990;21(2):387–400. http://doi.org/10.1007/BF02664206
17. Thomas B.G., Zhang L. Mathematical modeling of fluid flow in continuous casting. ISIJ International. 2001;41(10):1181–1193. http://doi.org/10.2355/isijinternational.41.1181
18. Yuan Q., Shi T., Vanka S.P., Thomas B.G. Simulation of turbulent flow and particle transport in the continuous casting of steel. In: Computational Modeling of Materials Minerals and Metals. Warrendale, PA; 2002:491–500.
19. Larreq M., Sagues C., Wanin M. Vodele mathematique de la solidification eu coulee continue tenant compte de la convection al`interface solide-liquide. Revue de Metallurgie. 1978;75(6):337–352.
20. Ozava M., Okano S., Matsuno J. Influence des contitions du jet de coulee sur la formation de la peau solidifiee eu lingotiere de brames de colee con-tinue. Tetsu-to-Hagane. 1976;62(4):86.
21. Kohn A., Morillon Y. Etnde mathematique de la solidification des lingots en acier mi-dur. Revue de Metallurgie. 1966;63(10):779–790.
22. Ho K., Pehlke R. Modelling of steel solidification using the general finite difference method. In: 5th Int. Iron and Steel Congress Proceedings of the 6th Process Technol. Conf. (Apr. 6–9, 1986). Warrendale; 1986;6:853–866.
23. Mizikar E. Mathematical heat transfer model for solidification of continuous cast steel slabs. Transactions of the Metallurgical Society of AIME. 1967;239(11):1747.
24. Szekely J., Stanek V. On heat transfer and liquid mixing in the continuous casting of steel. Metallurgical Transactions. 1970;1(1):119. https://doi.org/10.1007/BF02819250
25. Патент №2764446 РФ. Устройство для подачи и перемешивания стали в кристаллизаторе установки непрерывной разливки / Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Александров А.Ю., Карпенко В.А.; заявл. 20.05.2021; опубл. 17.01.2022. Бюл. № 2.
26. Одиноков В.И., Дмитриев Э.А., Евстигнеев А.И., Кузнецов С.А., Горнаков А.И. Совершенствование устройств по заполнению кристаллизатора УНРС жидким металлом. Металлург.2021;(4):33–35. https://doi.org/10.52351/00260827_2021_04_33
27. Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Александров С.Ю., Карпенко В.А. Совершенствование устройств для подачи и перемешивания жидкого металла в кристаллизаторе установки непрерывного литья стали. Заготовительные производства в машиностроении. 2022;20(3):99–103. https://doi.org/10.36652/1684-1107-2022-20-3-99-102
28. Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Карпенко В.А. Математическое моделирование процесса перемешивания жидкого металла в кристаллизаторе установке непрерывной разливки стали. Математическое моделирование и численные методы. 2023;(3):18–41.
29. Kim, W.S., Chair T.S. A simplified phenomenological theory of viscosity for liquid metals. Bulletin of the Korean Chemical Society. 2001;22(1):43–45.
Об авторах
В. И. ОдиноковРоссия
Валерий Иванович Одиноков, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
А. И. Евстигнеев
Россия
Алексей Иванович Евстигнеев, д.т.н., профессор, главный научный сотрудник Управления научно-исследовательской деятельностью
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Э. А. Дмитриев
Россия
Эдуард Анатольевич Дмитриев, д.т.н., доцент, ректор
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
В. А. Карпенко
Россия
Владимир Анатольевич Карпенко, соискатель степени к.т.н.
Россия, 681013, Хабаровский край, Комсомольск-на-Амуре, пр. Ленина, 27
Рецензия
Для цитирования:
Одиноков В.И., Евстигнеев А.И., Дмитриев Э.А., Карпенко В.А. Моделирование нового процесса перемешивания жидкого металла в кристаллизаторе установки непрерывной разливки стали при вращающейся рубашке с вертикальными ребрами. Известия высших учебных заведений. Черная Металлургия. 2023;66(6):733-742. https://doi.org/10.17073/0368-0797-2023-6-733-742
For citation:
Odinokov V.I., Evstigneev A.I., Dmitriev E.A., Karpenko V.A. Simulation of a new process of mixing liquid metal in CCM mold with rotating cooling jacket with vertical ribs. Izvestiya. Ferrous Metallurgy. 2023;66(6):733-742. https://doi.org/10.17073/0368-0797-2023-6-733-742
JATS XML