Scroll to:
Formation of the gradient of structural-phase states of high-speed steel during surfacing. Part 1. Solving the Stefan problem with two movable boundaries
https://doi.org/10.17073/0368-0797-2023-5-587-593
Abstract
The article considers theoretical study of solidification of the binary iron–tungsten system at a tungsten content of 18 wt. %. Such tungsten content is typical for heat-resistant alloys used in plasma-arc surfacing on the rolls surface. The axisymmetric Stefan thermal problem is solved for two movable cylindrical boundaries that separate three regions. In region 1, the melt is at the melting point; in region 2, the substance is in a two‒phase state, and in region 3 – a solid. The liquidus temperature was set at the interface of regions 1 and 2, and the solidus temperature – at the interface of regions 2 and 3. At these boundaries, a condition for the heat flows balance was given, from which a system of kinetic equations was obtained. This system was solved by numerical methods, without hypothesizing that the fronts of phase transformations move according to the law R ~ t1/2. Solution of the system of kinetic equations shows that the solidus boundary moves almost linearly. The liquidus boundary moves according to the parabolic law. For regions of the micrometer range in size, the processes of phase transformations take place in a time of about 5 ns, whereas for regions of the order of 10 μm in size – in a time of about 50 ms. Dependences of temperature fields on the radial coordinate at various points in time show that with increasing time, the dimensions of region 2 decrease, and as soon as coordinates of the liquidus and solidus boundaries become close, thecrystallization process stops. Further development of the model consists in taking into account the rotation of one of the media. The results obtained will serve as a material for the study of the Mullins-Sekerka two-front instability.
Keywords
For citations:
Nevskii S.A., Bashchenko L.P., Peregudov O.A. Formation of the gradient of structural-phase states of high-speed steel during surfacing. Part 1. Solving the Stefan problem with two movable boundaries. Izvestiya. Ferrous Metallurgy. 2023;66(5):587-593. https://doi.org/10.17073/0368-0797-2023-5-587-593
Introduction
The methods involving plasma surfacing of different wear-resistant materials are commonly employed for the restoration or repair of forming rolls [1]. Among the surfacing materials, there is a specific interest in heat-resistant iron-based alloys with elevated tungsten levels (approximately 17 – 18 %) and carbon content (0.76 – 0.82 %), renowned for their high hardness and exceptional wear resistance [2]. To prevent the formation of cold cracks during the application of coatings made from such alloys, pre-heating and controlled slow cooling of the parts are utilized [3]. However, post this treatment, the coatings exhibit reduced hardness and wear resistance. A complex heat treatment process (involving annealing, hardening, and tempering) becomes necessary to enhance these properties. Yet, this significantly restricts the potential applications of these considered alloys [4]. Hence, finding plasma surfacing methods for heat-resistant alloys that circumvent crack formation while preserving high mechanical and tribological properties without the need for additional thermal treatments is crucial. Addressing this challenge requires an understanding of the mechanisms governing the formation of gradient structural-phase states in materials during surfacing. The crystallization processes of the materials play a pivotal role in shaping these states [5], ultimately determining the resulting structure and hence, the mechanical properties achieved during the surfacing process.
Currently, numerous papers [5 – 10] expound upon mechanisms and models pertaining to the crystallization of materials on surfaces of various geometries. Depending on the external factors such as cooling rate, rotation speed, ambient temperature, degree of supercooling, among others, the resulting structure can manifest as cellular, dendritic, or a combination of both structures concurrently [5; 6]. One of the main mechanisms driving their formation, as proposed in [7; 8], involves the instability of the crystallization front induced by the temperature decrease during the phase transition, caused by the expulsion of impurities into the melt and the phenomenon of solutal undercooling. Hence, the configuration of the interfacial boundary significantly influences the impurity distribution within the crystal [9]. The central consensus across all theories of morphological stability is that when a specific balance between temperature and concentration gradients is reached, the crystallization front becomes unstable to minor perturbations [10]. Consequently, intricate structural-phase states emerge, facilitating particle nucleation on dissolved impurities. This leads to the creation of an extended phase transition region preceding the crystallization front [11]. Notably, the models outlined in [5 – 11] solely consider the displacement of phase transition boundaries, disregarding the displacement of melt heating boundaries. Typically, it is assumed that this boundary either maintains a stabilized temperature distribution or extends infinitely [12; 13]. Recognizing the outcomes of resolving the thermal problem, where the heating boundary is not considered infinitely large [14], reveals that the growth rate of particles accelerates in comparison to scenarios where this aspect is disregarded. Consequently, in the development of mathematical models concerning the impact of plasma on material structure, it becomes imperative to consider not only the displacement of phase transition boundaries but also the shifting boundaries of heating. In the quest to understand the mechanisms governing the formation of gradient structures and phase compositions in heat-resistant alloys during plasma surfacing on rotating rolls, integrating the concepts associated with the emergence and progression of the Mullins–Sekerka instability [15] becomes crucial. Analyzing this instability aids in determining the conditions for the onset of these states, taking into consideration the shifts in the heating boundary. This instability is studied through several stages: initially determining the nature of interface perturbations and evaluating the impact of its curvature on the liquidus temperature. Subsequently, calculations are performed for the temperature and concentration fields within the solid and liquid phases. This analysis includes identifying the dependency of the perturbation growth rate on the conditions existing at the phase transition boundary.
The focal point of this paper revolves around resolving the thermal and diffusion Stefan problem involving two movable boundaries. This approach facilitates the monitoring of material solidification kinetics. Unlike conventional studies [16 – 18] that rely on the assumption of crystal growth being directly proportional to t1/2 this hypothesis is deliberately avoided in this investigation. Instead, the evolution of crystal growth over time is tracked by solving a system of kinetic equations derived from temperature and substance balance conditions at the phase transition boundaries.
Research methodology (setting up a problem)
Let us examine the process of directional solidification along the spatial axis r in a cylindrical front. Fig. 1 illustrates the geometry of the problem.
Fig. 1. Diagram of the problem geometry |
The initial phase occupies the region R2(t) < r < +∞ (where t represents time) and maintains a temperature of T0 . When the temperature T\(^{**}\) is attained, the second phase forms, which occupies the region R1(t) < r < R2(t). At temperature T\(^*\), the third phase emerges within the region 0 < r < R1(t). Let us formulate the thermal conductivity equation for each of these distinct regions:
| \[\begin{array}{c}\frac{{\partial {T_1}}}{{\partial t}} = {\chi _1}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {T_1}}}{{\partial r}}} \right)} \right],{\rm{ }}{R_2}(t) < r < + \infty ;\\\frac{{\partial {T_2}}}{{\partial t}} = {\chi _2}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {T_2}}}{{\partial r}}} \right)} \right],{\rm{ }}{R_1}(t) < r < {R_2}(t);\\\frac{{\partial {T_3}}}{{\partial t}} = {\chi _3}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {T_3}}}{{\partial r}}} \right)} \right],{\rm{ }}0 < r < {R_1}(t),\end{array}\] | (1) |
where χ1 and χ2 , χ3 are thermal diffusivity coefficients in regions 1 ‒ 3.
The shift in phase transition boundaries is determined based on the balance conditions of temperature and heat flows, as expressed by equations (2):
| \[\begin{array}{c}{T_3} = {T_2} = {T^*},{\rm{ }}r = {R_1}(t);\\ - {\lambda _3}\frac{{\partial {T_3}}}{{\partial r}} + {\lambda _2}\frac{{\partial {T_2}}}{{\partial r}} = \Delta {H_1}\frac{{d{R_1}}}{{dt}},{\rm{ }}r = {R_1}(t);\\{T_2} = {T_1} = {T^{**}},{\rm{ }}r = {R_2}(t);\\{\lambda _1}\frac{{\partial {T_1}}}{{\partial r}} - {\lambda _2}\frac{{\partial {T_2}}}{{\partial r}} = \Delta {H_2}\frac{{d{R_2}}}{{dt}},{\rm{ }}r = {R_2}(t),\end{array}\] | (2) |
where λ1 and λ2 , λ3 are thermal conductivity coefficients in the regions 1 ‒ 3; ΔH1 and ΔH2 represent the volumetric heat of phase transformations.
At r → 0, the temperature is Tw1 , and at r → ∞, the temperature is T0 . The initial conditions are defined as
| \[{T_2}(r,{\rm{ }}0) = {T_0};{\rm{ }}{R_1}(0) = {R_0};{\rm{ }}{R_2}(0) = R_0^*,\] | (3) |
where R0 and \(R_0^*\) are the initial radii of the phase transition boundaries.
The solution of this system of equations (1) ‒ (3) is determined as follows
| \[{T_i}(r,{\rm{ }}t) = {A_i} + {B_i}{E_i}\left( {\frac{{{r^2}}}{{4{\chi _i}t}}} \right),\] | (4) |
where Ai , Bi are arbitrary constants; Ei (z) is an integral exponent; i = 1 ÷ 3.
Applying the boundary conditions (2) and initial conditions (3) to formula (4), the resulting solution is as follows:
| \[\begin{array}{c}{T_1}(r,{\rm{ }}t) = {T_0} - \left( {{T_0} - {T^{**}}} \right)\frac{{{E_i}\left( {\frac{{{r^2}}}{{4{\chi _1}t}}} \right)}}{{{E_i}\left( {\frac{{R_2^2}}{{4{\chi _1}t}}} \right)}},{\rm{ }}{R_2}(t) < r < + \infty ;\\{T_2}(r,{\rm{ }}t) = \frac{{{T^{**}}{E_i}\left( {\frac{{R_1^2}}{{4{\chi _2}t}}} \right) - {T^*}{E_i}\left( {\frac{{R_2^2}}{{4{\chi _2}t}}} \right) + \left( {{T^*} - {T^{**}}} \right){E_i}\left( {\frac{{{r^2}}}{{4{\chi _2}t}}} \right)}}{{{E_i}\left( {\frac{{{R_1}}}{{4{\chi _2}t}}} \right) - {E_i}\left( {\frac{{{R_2}}}{{4{\chi _2}t}}} \right)}},\\{R_1}(t) < r < {R_2}(t);\\{T_3}(r,{\rm{ }}t) = \frac{{{T^*}{E_i}\left( {\frac{{R_{}^2}}{{4{\chi _3}t}}} \right) - {T_{w1}}{E_i}\left( {\frac{{R_1^2}}{{4{\chi _3}t}}} \right) - \left( {{T^*} - {T_{w1}}} \right){E_i}\left( {\frac{{{r^2}}}{{4{\chi _3}t}}} \right)}}{{{E_i}\left( {\frac{{{R^2}}}{{4{\chi _3}t}}} \right) - {E_i}\left( {\frac{{R_1^2}}{{4{\chi _3}t}}} \right)}},\\0 < r < {R_1}(t).\end{array}\] | (5) |
The parameter R, introduced to prevent divergence at r → 0, is assigned a value of 10\(^–\)8 m to eliminate the singularity at this point in the radial coordinate.
Results and discussion
As equation (5) is integrated into the heat balance equations at the boundaries of phase transitions, the resulting kinetic equations are as follows:
| \[\begin{array}{c}\frac{{d{R_1}}}{{dt}} = \frac{{\left[ {{F_1}\exp \left( { - \frac{{R_1^2}}{{4{\chi _1}t}}} \right)} \right] - \left[ {{F_2}\exp \left( { - \frac{{R_1^2}}{{4{\chi _3}t}}} \right)} \right]}}{{{R_1}\left[ {{E_i}\left( {\frac{{R_1^2}}{{4{\chi _2}t}}} \right) - {E_i}\left( {\frac{{R_2^2}}{{4{\chi _2}t}}} \right)} \right]}};\\\frac{{d{R_2}}}{{dt}} = \frac{{{G_1}\exp \left( { - \frac{{R_2^2}}{{4{\chi _2}t}}} \right)}}{{{R_2}\left[ {{E_i}\left( {\frac{{R_1^2}}{{4{\chi _2}t}}} \right) - {E_i}\left( {\frac{{R_2^2}}{{4{\chi _2}t}}} \right)} \right]}} - \frac{{{G_2}\exp \left( { - \frac{{R_2^2}}{{4{\chi _1}t}}} \right)}}{{{R_2}\left[ {{E_i}\left( {\frac{{R_2^2}}{{4{\chi _1}t}}} \right)} \right]}};\\{F_1} = \frac{{2\left( {{T^{**}} - {T^*}} \right){\lambda _2}}}{{\Delta {H_1}}};{\rm{ }}{F_2} = \frac{{2\left( {{T^*} - {T_{w1}}} \right){\lambda _3}}}{{\Delta {H_1}}};\,\\{G_1} = \frac{{2\left( {{T^*} - {T^{**}}} \right){\lambda _2}}}{{\Delta {H_2}}};{\rm{ }}{G_2} = \frac{{2\left( {{T_0} - {T^{**}}} \right){\lambda _1}}}{{\Delta {H_2}}}.\end{array}\] | (6) |
The system (6) of ordinary differential equations is resolved using the high-order Runge-Kutta method. To simplify the mathematical computations, non-dimensional variables \({\tilde R_i} = \frac{R}{{{R_0}}}\) and \(\tau = t\frac{{{\chi _1}}}{{R_0^2}}\) (where τ is nondimensional time) were employed. Given that as at t → 0 the function \({E_i}\frac{{R_i^2}}{{4\chi t}} \to 0,\) the initial time value was set to 10\(^–\)9 s. The characteristics of the investigated material, specifically, iron – tungsten system, are outlined in the table provided.
Characteristics of the iron – tungsten system
|
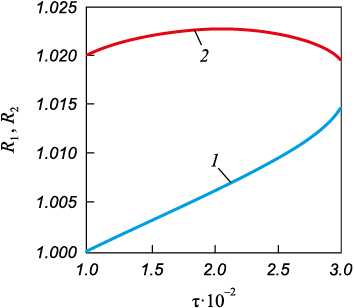
In region 1 the initial melt temperature was set at T0 = 1811 K. At the R2 boundary, the liquidus temperature T\(^{**}\) is 1806 K, while at the R1 boundary, the solidus temperature T\(^*\) s 1803 K. These temperatures were determined based on the state diagram [19] for an 18 wt. % tungsten content. The temperature Tw1 was assumed to be lower than T\(^*\) and measured at 1790 K. It was considered that χ2 = χ3 and λ2 = λ3 , along with ΔН1 = ΔН2 . Fig. 2 displays the dependencies of the interface movements. At R0 = 1 μm, the boundary coordinate R1 exhibits nearly linear growth until τ = 0.028 (4.4118 ns), while R2 demonstrates non-monotonic changes, decreasing after τ > 0.028 (4.4118 ns). For R0 = 10 μm, a similar trend is observed yet the crystallization process takes place over a longer duration of 41.176 μs.
Fig. 2. Dependences of radial coordinates of crystallization front on time |
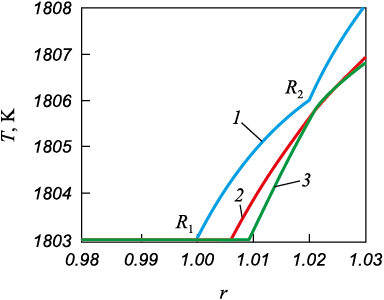
The results suggest that with a reduction in the size of nuclei, the duration of their steady growth significantly decreases by almost four orders of magnitude. The abrupt decline in the radial coordinate R2 , may indicate instability in the crystallization front, potentially due to interfacial surface tension and supercooling effects. The rapidity of the crystallization process in smaller regions is attributed to a high surface energy, which aims to decrease through size growth and interface configuration changes. In Fig. 3, the temperature dependencies plotted against the non-dimensional radial coordinate illustrate a notable trend: as time progresses, region 2 demonstrates a reduction in size (represented by curves 2 and 3), while conversely, region 3, displays growth.
Fig. 3. Temperature dependences on the coordinate |
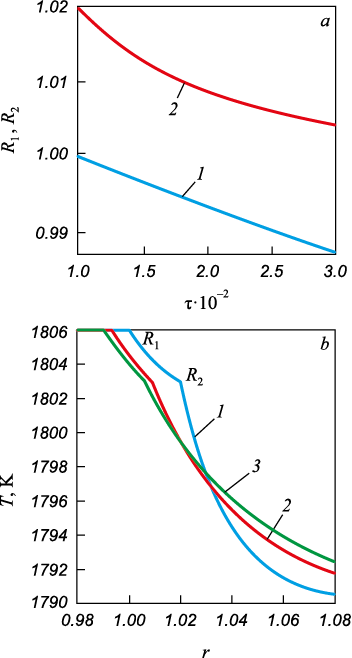
In the scenario where T0 = 1790 K, T\(^{**}\) = 1803 K, T\(^*\) = 1803 K and Tw1 = 1811 K (Fig. 4). The coordinates of the phase transition boundaries exhibit a reduction (Fig. 4, a), with R1 decreasing linearly while R2 follows a parabolic trajectory. Temperature dependences (Fig. 4, b) indicate a similar trend to the previous case, wherein regions 2 and 3 (curves 2 and 3) experience a decrease in size.
Fig. 4. Calculation results for Tw1 = 1811 K, |
Conclusions
The theoretical investigation of the crystallization process within the iron – tungsten system, conducted by solving kinetic equations, revealed intriguing behavior. Specifically, it was observed that the movement of the liquidus boundary R2 follows a descending parabolic trajectory, contrary to the expected R ~ t1/2 law, whereas the solidus boundary R1 exhibits almost linear movement. Upon reaching a certain time threshold, the convergence of these boundaries occurs, indicating either the cessation of the crystallization process or the onset of crystallization front instability. The temperature dependencies derived from this study will serve as a foundational framework for further exploration of this observed instability. As the model progresses and adapts to simulate the plasma-arc surfacing process of rolls, future iterations will consider factors such as the rotation of one of the media involved and a more precise incorporation of the concentration of alloying elements.
References
1. Sosnin N.A., Ermakov S.A., Topolyanskii P.A. Plasma Technologies. A Guide for Engineers. SPb.: izd. Politekhnicheskogo un-ta; 2013;406. (In Russ.).
2. Damon J., Schüßler P., Mühl F., Dietrich S., Schulze V. Short-time induction heat treatment of high speed steel AISI M2: Laboratory proof of concept and application-related component tests. Materials & Design. 2023;230:111991. https://doi.org/10.1016/j.matdes.2023.111991
3. Park G.-W., Shin S., Kim J.-Y., Koo Y.-M., Lee W., Lee K.-A., Park S.S., Jeon J.B. Analysis of solidification microstructure and cracking mechanism of a matrix high-speed steel deposited using directed-energy deposition. Journal of Alloys and Compounds. 2022;907:164523. https://doi.org/10.1016/j.jallcom.2022.164523
4. Malushin N.N., Romanov D.A., Kovalev A.P., Osetkovskii V.L., Bashchenko L.P. Structural-phase state of a heat-resistant alloy of high hardness formed by plasma surfacing in nitrogen medium and high-temperature tempering. Izvestiya vuzov. Fizika. 2019;62(10(742)):106–111. (In Russ.). https://doi.org/10.17223/00213411/62/10/106
5. Aleksandrov D.V., Aleksandrova I.V., Ivanov A.A., Malygin A.P., Nizovtseva I.G. Nonlinear analysis of the stability of solidification with a mushy zone. Russian Metallurgy (Metally). 2014;2014(8):606–617. https://doi.org/10.1134/S0036029514080035
6. Aleksandrov D.V., Aleksandrova I.V., Ivanov A.A., Starodumov I.O., Toropova L.V. Directional solidification with a two-phase zone taking into account the dependence of liquid phase density on temperature and impurity concentration. Rasplavy. 2020;(1):37‒45. (In Russ.). https://doi.org/10.31857/S0235010620010028
7. Alexandrov D.V., Toropova L.V. The role of incoming flow on crystallization of undercooled liquids with a two‑phase layer. Scientific Reports. 2022;12:17857. https://doi.org/10.1038/s41598-022-22786-w
8. Worster M.G. Natural convection in a mushy layer. Journal of Fluid Mechanics. 1991;224:335–359. https://doi.org/10.1017/S0022112091001787
9. Lahiri A., Choudhury A. Theoretical and numerical investigation of diffusive instabilities in multicomponent alloys. Journal of Crystal Growth. 2017;459:1–12. http://dx.doi.org/10.1016/j.jcrysgro.2016.11.046
10. Sekerka R.F. Morphological stability. Journal of Crystal Growth. 1968;3-4:71–81. https://doi.org/10.1016/0022-0248(68)90102-4
11. Alexandrov D.V. Solidification with a quasiequilibrium mushy region: exact analytical solution of nonlinear model. Journal of Crystal Growth. 2001;222(4):816–821. https://doi.org/10.1016/S0022-0248(00)00960-X
12. Elsaid A., Helal S.M. Moving Taylor series for solving one-dimensional one-phase Stefan problem. Alexandria Engineering Journal. 2022;61(9):7121–7128. https://doi.org/10.1016/j.aej.2021.12.055
13. Lykov A.V. Theory of Thermal Conductivity. Moscow: Vysshaya shkola; 1967;599. (In Russ.).
14. Sergeev S.A. Mathematical modeling of unsteady thermal conductivity of spherical particle crystallization in a melt with moving boundaries. Issledovano v Rossii. 2003;(6):664–672.
15. Chen M.W., Wang Z.D. The evolution and morphological stability of a particle in a binary alloy melt. Journal of Crystal Growth. 2023;607:127113. https://doi.org/10.1016/j.jcrysgro.2023.127113
16. Formalev V.F., Rabinskii L.N. On a Stefan-type problem with two unsteadily moving boundaries of phase transformations. Izvestiya RAN. Energetika. 2014;(4):74–81. (In Russ.).
17. Kartashov E.M. Analytical methods for solving boundary value problems of unsteady thermal conductivity in regions with moving boundaries. Engineering and Physics Journal. 2001;74(2):171–195.
18. Carslaw H.S., Jaeger J.C. Conduction of Heat in Solids. London: Oxford University Press; 1947.
19. Lyakishev N.P. State Diagrams of Double Metal Systems. In 3 vols. Vol. 2. Moscow: Mashinostroenie; 1997;1024. (In Russ.).
20. Chen M.-W., Wang Y., Guo H. The effect of anisotropic surface tension on interfacial evolution of a particle in the binary alloy melt. Journal of Crystal Growth. 2019;510:32‒39. https://doi.org/10.1016/j.jcrysgro.2018.12.032
About the Authors
S. A. NevskiiRussian Federation
Sergei A. Nevskii, Dr. Sci. (Eng.), Assist. Prof. of the Chair of Natural Sciences named after Professor V.M. Finkel
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
L. P. Bashchenko
Russian Federation
Lyudmila P. Bashchenko, Cand. Sci. (Eng.), Assist. Prof. of the Chair “Thermal Power and Ecology”
42 Kirova Str., Novokuznetsk, Kemerovo Region – Kuzbass 654007, Russian Federation
O. A. Peregudov
Russian Federation
Oleg A. Peregudov, Cand. Sci. (Eng.), Vice-Rector for Youth Policy and Educational Activities
11 Mira Ave., Omsk 644050, Russian Federation
Review
For citations:
Nevskii S.A., Bashchenko L.P., Peregudov O.A. Formation of the gradient of structural-phase states of high-speed steel during surfacing. Part 1. Solving the Stefan problem with two movable boundaries. Izvestiya. Ferrous Metallurgy. 2023;66(5):587-593. https://doi.org/10.17073/0368-0797-2023-5-587-593
JATS XML