Перейти к:
Формирование градиента структурно-фазовых состояний быстрорежущей стали при наплавке. Часть 1. Решение задачи Стефана с двумя подвижными границами
https://doi.org/10.17073/0368-0797-2023-5-587-593
Аннотация
Теоретически рассматривается процесс затвердевания бинарной системы железо – вольфрам при содержании вольфрама 18 % (по массе). Такое содержание вольфрама характерно для теплостойкого сплава, который применяется в процессах плазменно-дуговой наплавки на поверхность валков. Решается осесимметричная тепловая задача Стефана для двух подвижных цилиндрических границ, которые разделяют три области. В области 1 расплав находится при температуре плавления, в области 2 вещество находится в двухфазном состоянии, а в области 3 ‒ твердое тело. На границе раздела областей 1 и 2 задается температура ликвидуса, а на границе раздела 2 и 3 – температура солидуса. На данных границах задается условие баланса тепловых потоков, из которого получена система кинетических уравнений. Эту систему решали численными методами, при этом не выдвигались гипотезы о том, что фронты фазовых превращений движутся по закону R ~ t1/2. Решение системы кинетических уравнений показывает, что граница солидуса движется практически по линейному закону. Граница ликвидуса перемещается по параболическому закону. Для областей микрометрового диапазона по размерам процессы фазовых превращений протекают за время порядка 5 нс, тогда как для областей размерами порядка 10 мкм – за время около 50 мкс. Зависимости температурных полей от радиальной координаты в различные моменты времени показывают, что с увеличением времени размеры области 2 уменьшаются, и, как только значения координат границ ликвидуса и солидуса становятся близкими, процесс кристаллизации останавливается. Дальнейшее развитие модели заключается в учете вращения одной из сред. Полученные результаты послужат материалом для исследования двухфронтовой неустойчивости Маллинза-Секерки.
Ключевые слова
Для цитирования:
Невский С.А., Бащенко Л.П., Перегудов О.А. Формирование градиента структурно-фазовых состояний быстрорежущей стали при наплавке. Часть 1. Решение задачи Стефана с двумя подвижными границами. Известия высших учебных заведений. Черная Металлургия. 2023;66(5):587-593. https://doi.org/10.17073/0368-0797-2023-5-587-593
For citation:
Nevskii S.A., Bashchenko L.P., Peregudov O.A. Formation of the gradient of structural-phase states of high-speed steel during surfacing. Part 1. Solving the Stefan problem with two movable boundaries. Izvestiya. Ferrous Metallurgy. 2023;66(5):587-593. https://doi.org/10.17073/0368-0797-2023-5-587-593
Введение
Для ремонта прокатных валков традиционно применяются технологии плазменной наплавки различных износостойких материалов [1]. В качестве наплавочных материалов особый интерес представляют теплостойкие сплавы на основе железа с высокими содержаниями вольфрама (примерно 17 – 18 %) и углерода (0,76 – 0,82 %), которые обладают высокими твердостью и износостойкостью [2]. Нанесение покрытий из таких сплавов сопровождается образованием холодных трещин, для борьбы с которыми применяют предварительный и сопутствующий высокотемпературный подогрев и замедленное охлаждение деталей [3]. Однако при такой обработке полученные покрытия имеют низкие твердость и износостойкость. Для их повышения необходимо проведение дополнительной термической обработки по сложной схеме отжиг – закалка – отпуск. Это сильно ограничивает применение рассматриваемых сплавов [4]. В этой связи актуален поиск способов плазменной наплавки теплостойких сплавов, которые позволяют избежать образования трещин и сохранить высокие механические и трибологические свойства без применения дополнительных термических обработок. Решение этой задачи требует наличия сведений о механизмах формирования градиентных структурно-фазовых состояний в материалах при наплавке. Фундаментальную роль в образовании данных состояний играют процессы кристаллизации материалов [5]. От протекания этих процессов будет зависеть, какая структура и, соответственно, какие механические свойства будут получены в ходе наплавки.
В настоящее время механизмам и моделям кристаллизации материалов на поверхностях различной геометрии посвящено множество работ [5 – 10]. В зависимости от внешних условий (скорости охлаждения, скорости вращения, температуры окружающей среды, степени переохлаждения и т.д.) образуется ячеистая или дендритная структура, либо одновременно существуют обе структуры [5; 6]. Одним из основных механизмов их образования, по мнению авторов работ [7; 8], является неустойчивость фронта кристаллизации, вызванная понижением температуры фазового перехода вследствие вытеснения примеси в расплав, а также явлением концентрационного переохлаждения. Таким образом, форма межфазной границы оказывает определяющее влияние на распределение примесей в кристалле [9]. Основной вывод всех теорий морфологической устойчивости заключается в том, что при определенном соотношении между температурным и концентрационным градиентами происходит потеря устойчивости фронта кристаллизации по отношению к малым возмущениям [10]. Это приводит к образованию сложных структурно-фазовых состояний, а также способствует протеканию процесса нуклеации частиц на растворенных примесях. Таким образом, перед фронтом кристаллизации возникает протяженная область фазового перехода [11]. Представленные в работах [5 – 11] модели учитывают только движение границ фазового перехода, но не рассматривают движение границ прогрева расплава. Обычно предполагается, что на данной границе наблюдается стабилизированное распределение температуры или ее устремляют в бесконечность [12; 13]. Учет того, что граница прогрева не является бесконечно большой, согласно результатам решения тепловой задачи [14] приводит к более быстрому росту частиц по сравнению с решением задач без учета данного факта. Таким образом, при построении математических моделей плазменного воздействия на структуру материалов необходимо учитывать как движение границ фазового перехода, так и границ прогрева. Поиск механизмов формирования градиента структуры и фазового состава теплостойких сплавов при плазменной наплавке на вращающийся валок необходимо проводить с использованием представлений о возникновении и развитии неустойчивости Маллинза-Секерки [15], анализ которой позволяет определить условия возникновения этих состояний с учетом движения границы прогрева. Изучение этой неустойчивости проводится в несколько этапов: определение характера возмущений поверхности раздела и оценка влияния ее кривизны на температуру ликвидуса; расчет полей температур и концентраций в твердой и жидкой фазе; нахождение зависимости скорости роста возмущений из условий на границе фазового перехода.
В настоящей работе особое внимание уделяется решению тепловой и диффузионной задачи Стефана для двух подвижных границ, что позволит отследить кинетику затвердевания материала. В отличие от традиционных работ [16 – 18] по решению данной задачи, где предполагается, что рост кристалла прямо пропорционален величине t1/2, в настоящей работе данная гипотеза не используется. Процесс роста кристалла во времени отслеживается путем решения системы кинетических уравнений, полученных из условий баланса температуры и вещества на границах фазовых переходов.
Методика проведения исследований (постановка задачи)
Рассмотрим процесс направленного затвердевания цилиндрического фронта вдоль пространственной оси r. На рис. 1 приведена схема геометрии задачи.
Рис. 1. Схема геометрии задачи |
Исходная фаза занимает область R2(t) < r < +∞ (где t – время) и обладает температурой T0 . По мере достижения температуры T\(^{**}\) образуется вторая фаза, которая занимает область R1(t) < r < R2(t). При температуре T\(^*\) образуется третья фаза, которая находится в области 0 < r < R1(t). Для каждой из областей запишем уравнение теплопроводности:
| \[\begin{array}{c}\frac{{\partial {T_1}}}{{\partial t}} = {\chi _1}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {T_1}}}{{\partial r}}} \right)} \right],{\rm{ }}{R_2}(t) < r < + \infty ;\\\frac{{\partial {T_2}}}{{\partial t}} = {\chi _2}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {T_2}}}{{\partial r}}} \right)} \right],{\rm{ }}{R_1}(t) < r < {R_2}(t);\\\frac{{\partial {T_3}}}{{\partial t}} = {\chi _3}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {T_3}}}{{\partial r}}} \right)} \right],{\rm{ }}0 < r < {R_1}(t),\end{array}\] | (1) |
где χ1 и χ2 , χ3 – коэффициенты температуропроводности в областях 1 ‒ 3.
Движение границ фазовых переходов будет определяться из условий баланса температур и тепловых потоков:
| \[\begin{array}{c}{T_3} = {T_2} = {T^*},{\rm{ }}r = {R_1}(t);\\ - {\lambda _3}\frac{{\partial {T_3}}}{{\partial r}} + {\lambda _2}\frac{{\partial {T_2}}}{{\partial r}} = \Delta {H_1}\frac{{d{R_1}}}{{dt}},{\rm{ }}r = {R_1}(t);\\{T_2} = {T_1} = {T^{**}},{\rm{ }}r = {R_2}(t);\\{\lambda _1}\frac{{\partial {T_1}}}{{\partial r}} - {\lambda _2}\frac{{\partial {T_2}}}{{\partial r}} = \Delta {H_2}\frac{{d{R_2}}}{{dt}},{\rm{ }}r = {R_2}(t),\end{array}\] | (2) |
где λ1 и λ2 , λ3 – коэффициенты теплопроводности в областях 1 ‒ 3; ΔH1 и ΔH2 ‒ объемная теплота фазовых превращений.
При r → 0 значение температуры составляет Tw1 , а при r → ∞ значение температуры T0 . Начальные условия будут иметь вид
| \[{T_2}(r,{\rm{ }}0) = {T_0};{\rm{ }}{R_1}(0) = {R_0};{\rm{ }}{R_2}(0) = R_0^*,\] | (3) |
где R0 и \(R_0^*\) ‒ начальные радиусы границ фазовых переходов.
Решение системы (1) ‒ (3) будем искать в виде
| \[{T_i}(r,{\rm{ }}t) = {A_i} + {B_i}{E_i}\left( {\frac{{{r^2}}}{{4{\chi _i}t}}} \right),\] | (4) |
где Ai , Bi – произвольные постоянные; Ei (z) ‒ интегральная показательная функция; i = 1 ÷ 3.
Подставляя в выражение (4) граничные условия (2) и начальные условия (3), получим:
| \[\begin{array}{c}{T_1}(r,{\rm{ }}t) = {T_0} - \left( {{T_0} - {T^{**}}} \right)\frac{{{E_i}\left( {\frac{{{r^2}}}{{4{\chi _1}t}}} \right)}}{{{E_i}\left( {\frac{{R_2^2}}{{4{\chi _1}t}}} \right)}},{\rm{ }}{R_2}(t) < r < + \infty ;\\{T_2}(r,{\rm{ }}t) = \frac{{{T^{**}}{E_i}\left( {\frac{{R_1^2}}{{4{\chi _2}t}}} \right) - {T^*}{E_i}\left( {\frac{{R_2^2}}{{4{\chi _2}t}}} \right) + \left( {{T^*} - {T^{**}}} \right){E_i}\left( {\frac{{{r^2}}}{{4{\chi _2}t}}} \right)}}{{{E_i}\left( {\frac{{{R_1}}}{{4{\chi _2}t}}} \right) - {E_i}\left( {\frac{{{R_2}}}{{4{\chi _2}t}}} \right)}},\\{R_1}(t) < r < {R_2}(t);\\{T_3}(r,{\rm{ }}t) = \frac{{{T^*}{E_i}\left( {\frac{{R_{}^2}}{{4{\chi _3}t}}} \right) - {T_{w1}}{E_i}\left( {\frac{{R_1^2}}{{4{\chi _3}t}}} \right) - \left( {{T^*} - {T_{w1}}} \right){E_i}\left( {\frac{{{r^2}}}{{4{\chi _3}t}}} \right)}}{{{E_i}\left( {\frac{{{R^2}}}{{4{\chi _3}t}}} \right) - {E_i}\left( {\frac{{R_1^2}}{{4{\chi _3}t}}} \right)}},\\0 < r < {R_1}(t).\end{array}\] | (5) |
Параметр R, который имеет размерность радиальной координаты, выбран для устранения расходимости при r → 0. Его значение предполагается равным 10\(^–\)8 м.
Результаты и их обсуждение
Подстановка зависимости (5) в уравнения теплового баланса на границах фазовых переходов приводит к следующим кинетическим уравнениям:
| \[\begin{array}{c}\frac{{d{R_1}}}{{dt}} = \frac{{\left[ {{F_1}\exp \left( { - \frac{{R_1^2}}{{4{\chi _1}t}}} \right)} \right] - \left[ {{F_2}\exp \left( { - \frac{{R_1^2}}{{4{\chi _3}t}}} \right)} \right]}}{{{R_1}\left[ {{E_i}\left( {\frac{{R_1^2}}{{4{\chi _2}t}}} \right) - {E_i}\left( {\frac{{R_2^2}}{{4{\chi _2}t}}} \right)} \right]}};\\\frac{{d{R_2}}}{{dt}} = \frac{{{G_1}\exp \left( { - \frac{{R_2^2}}{{4{\chi _2}t}}} \right)}}{{{R_2}\left[ {{E_i}\left( {\frac{{R_1^2}}{{4{\chi _2}t}}} \right) - {E_i}\left( {\frac{{R_2^2}}{{4{\chi _2}t}}} \right)} \right]}} - \frac{{{G_2}\exp \left( { - \frac{{R_2^2}}{{4{\chi _1}t}}} \right)}}{{{R_2}\left[ {{E_i}\left( {\frac{{R_2^2}}{{4{\chi _1}t}}} \right)} \right]}};\\{F_1} = \frac{{2\left( {{T^{**}} - {T^*}} \right){\lambda _2}}}{{\Delta {H_1}}};{\rm{ }}{F_2} = \frac{{2\left( {{T^*} - {T_{w1}}} \right){\lambda _3}}}{{\Delta {H_1}}};\,\\{G_1} = \frac{{2\left( {{T^*} - {T^{**}}} \right){\lambda _2}}}{{\Delta {H_2}}};{\rm{ }}{G_2} = \frac{{2\left( {{T_0} - {T^{**}}} \right){\lambda _1}}}{{\Delta {H_2}}}.\end{array}\] | (6) |
Система (6) обыкновенных дифференциальных уравнений решается методом Рунге-Кутта высокого порядка. Для удобства расчетов были использованы безразмерные переменные \({\tilde R_i} = \frac{R}{{{R_0}}}\) и \(\tau = t\frac{{{\chi _1}}}{{R_0^2}}\) (τ – безразмерное время). Так как при t → 0 функция \({E_i}\frac{{R_i^2}}{{4\chi t}} \to 0,\) то значение времени задавалось порядка 10\(^–\)9 с. Характеристики исследуемого материала (системы железо – вольфрам) приведены в таблице.
Характеристики системы железо – вольфрам
|
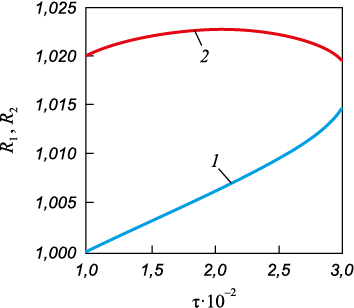
В области 1 задавалась температура расплава T0 = 1811 К. На границе R2 температура ликвидуса T\(^{**}\) составляет 1806 К, а на границе R1 температура солидуса T\(^*\) составляет 1803 К. Эти значения температур определялись по диаграмме состояния [19] при содержании вольфрама 18 % (по массе). Температура Tw1 меньше T\(^*\) и составляла 1790 К. Предполагалось, что χ2 = χ3 и λ2 = λ3 , ΔН1 = ΔН2 . На рис. 2 представлены зависимости движения границ раздела. При R0 = 1 мкм координата границы R1 увеличивается практически по линейному закону до τ = 0,028 (4,4118 нс), тогда как R2 изменяется немонотонно, резко снижаясь после τ > 0,028 (4,4118 нс). Если R0 = 10 мкм, то будет наблюдаться такая же тенденция с той лишь разницей, что длительность процесса кристаллизации будет составлять 41,176 мкс.
Рис. 2. Зависимости радиальных координат фронта кристаллизации |
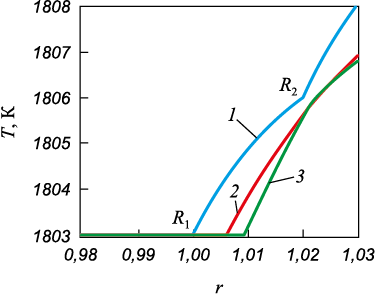
Полученные результаты позволяют сделать вывод, что с уменьшением размера зародышей время их устойчивого роста уменьшается практически на четыре порядка. Резкое снижение значения радиальной координаты R2 , такое же резкое увеличение координаты R1 могут свидетельствовать о возникновении неустойчивости фронта кристаллизации, которая вызывается как наличием межфазного поверхностного натяжения, так и переохлаждением. Быстрое протекание процесса кристаллизации в областях малых размеров объясняется наличием большой поверхностной энергии, которая стремится уменьшиться за счет роста размеров и изменения конфигурации границы раздела сред [20]. На рис. 3 представлены зависимости температуры от безразмерной радиальной координаты. Видно, что с увеличением времени размеры области 2 уменьшаются (кривые 2 и 3), тогда как размеры области 3, увеличиваются.
Рис. 3. Зависимости температуры от координаты в различные |
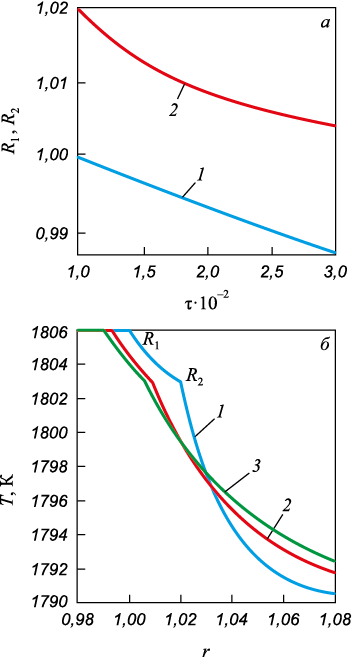
Другая тенденция будет наблюдаться при T0 = 1790 К, T\(^{**}\) = 1803 К, T\(^*\) = 1803 К и Tw1 = 1811 К (рис. 4). Координаты границ фазовых переходов будут уменьшаться (рис. 4, а), причем R1 по линейному закону, а R2 по параболическому. Зависимости температуры (рис. 4, б) показывают, что, как и в предыдущем случае, наблюдается снижение размеров областей 2 и 3 (кривые 2 и 3).
Рис. 4. Результаты вычислений при Tw1 = 1811 К, |
Выводы
Проведенное теоретическое исследование процесса кристаллизации системы на примере железо – вольфрам путем решения кинетических уравнений показало, что граница ликвидуса R2 движется не по закону R ~ t1/2, а по нисходящей параболе, граница солидуса R1 движется практически по линейному закону. По достижении определенного значения времени наблюдается сближение данных границ, что говорит об остановке процесса кристаллизации или о развитии неустойчивости фронта кристаллизации. Полученные температурные зависимости послужат основой для изучения этой неустойчивости. Дальнейшее развитие модели в направлении ее адаптации к процессу плазменно-дуговой наплавки валков заключается в учете вращения одной из сред и более строгом учете влияния концентрации легирующих элементов.
Список литературы
1. Соснин Н.А., Ермаков С.А., Тополянский П.А. Плазменные технологии. Руководство для инженеров. СПб.: изд. Политехнического ун-та; 2013;406.
2. Damon J., Schüßler P., Mühl F., Dietrich S., Schulze V. Short-time induction heat treatment of high speed steel AISI M2: Laboratory proof of concept and application-related component tests. Materials & Design. 2023;230:111991. https://doi.org/10.1016/j.matdes.2023.111991
3. Park G.-W., Shin S., Kim J.-Y., Koo Y.-M., Lee W., Lee K.-A., Park S.S., Jeon J.B. Analysis of solidification microstructure and cracking mechanism of a matrix high-speed steel deposited using directed-energy deposition. Journal of Alloys and Compounds. 2022;907:164523. https://doi.org/10.1016/j.jallcom.2022.164523
4. Малушин Н.Н., Романов Д.А., Ковалев А.П., Осетковский В.Л., Бащенко Л.П. Структурно-фазовое состояние теплостойкого сплава высокой твердости, сформированного плазменной наплавкой в среде азота и высокотемпературным отпуском. Известия вузов. Физика. 2019;62(10(742)):106–111. https://doi.org/10.17223/00213411/62/10/106
5. Александров Д.В., Александрова И.В., Иванов А.А., Малыгин А.П., Низовцева И.Г. Нелинейный анализ устойчивости затвердевания c областью фазового перехода. Расплавы. 2014;(2)27‒40.
6. Александров Д.В., Александрова И.В., Иванов А.А., Стародумов И.О., Торопова Л.В. Направленное затвердевание с двухфазной зоной с учетом зависимости плотности жидкой фазы от температуры и концентрации примеси. Расплавы. 2020;(1):37‒45. https://doi.org/10.31857/S0235010620010028
7. Alexandrov D.V., Toropova L.V. The role of incoming flow on crystallization of undercooled liquids with a two‑phase layer. Scientific Reports. 2022;12:17857. https://doi.org/10.1038/s41598-022-22786-w
8. Worster M.G. Natural convection in a mushy layer. Journal of Fluid Mechanics. 1991;224:335–359. https://doi.org/10.1017/S0022112091001787
9. Lahiri A., Choudhury A. Theoretical and numerical investigation of diffusive instabilities in multicomponent alloys. Journal of Crystal Growth. 2017;459:1–12. http://dx.doi.org/10.1016/j.jcrysgro.2016.11.046
10. Sekerka R.F. Morphological stability. Journal of Crystal Growth. 1968;3-4:71–81. https://doi.org/10.1016/0022-0248(68)90102-4
11. Alexandrov D.V. Solidification with a quasiequilibrium mushy region: exact analytical solution of nonlinear model. Journal of Crystal Growth. 2001;222(4):816–821. https://doi.org/10.1016/S0022-0248(00)00960-X
12. Elsaid A., Helal S.M. Moving Taylor series for solving one-dimensional one-phase Stefan problem. Alexandria Engineering Journal. 2022;61(9):7121–7128. https://doi.org/10.1016/j.aej.2021.12.055
13. Лыков А.В. Теория теплопроводности. Москва: Высшая школа; 1967;599.
14. Сергеев С.А. Математическое моделирование нестационарной теплопроводности кристаллизации частицы сферической формы в расплаве с движущимися границами. Исследовано в России. 2003;6:664–672.
15. Chen M.W., Wang Z.D. The evolution and morphological stability of a particle in a binary alloy melt. Journal of Crystal Growth. 2023;607:127113. https://doi.org/10.1016/j.jcrysgro.2023.127113
16. Формалев В.Ф., Рабинский Л.Н. О задаче типа Стефана с двумя нестационарно подвижными границами фазовых превращений. Известия РАН. Энергетика. 2014;(4):74–81.
17. Карташов Э.М. Аналитические методы решения краевых задач нестационарной теплопроводности в областях с движущимися границами. Инженерно-физический журнал. 2001;74(2):171–195.
18. Карслоу Г., Егер Д. Теплопроводность твердых тел. Москва: Наука; 1964;488.
19. Лякишев Н.П. Диаграммы состояния двойных металлических систем. В 3 т. Т. 2. Москва: Машиностроение; 1997;1024.
20. Chen M.-W., Wang Y., Guo H. The effect of anisotropic surface tension on interfacial evolution of a particle in the binary alloy melt. Journal of Crystal Growth. 2019;510:32‒39. https://doi.org/10.1016/j.jcrysgro.2018.12.032
Об авторах
С. А. НевскийРоссия
Сергей Андреевич Невский, д.т.н., доцент кафедры естественнонаучных дисциплин им. профессора В.М. Финкеля
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Л. П. Бащенко
Россия
Людмила Петровна Бащенко, к.т.н., доцент кафедры теплоэнергетики и экологии
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
О. А. Перегудов
Россия
Олег Александрович Перегудов, к.т.н., проректор по молодежной политике и воспитательной деятельности
Россия, 644050, Омск, пр. Мира, 11
Рецензия
Для цитирования:
Невский С.А., Бащенко Л.П., Перегудов О.А. Формирование градиента структурно-фазовых состояний быстрорежущей стали при наплавке. Часть 1. Решение задачи Стефана с двумя подвижными границами. Известия высших учебных заведений. Черная Металлургия. 2023;66(5):587-593. https://doi.org/10.17073/0368-0797-2023-5-587-593
For citation:
Nevskii S.A., Bashchenko L.P., Peregudov O.A. Formation of the gradient of structural-phase states of high-speed steel during surfacing. Part 1. Solving the Stefan problem with two movable boundaries. Izvestiya. Ferrous Metallurgy. 2023;66(5):587-593. https://doi.org/10.17073/0368-0797-2023-5-587-593
JATS XML