Перейти к:
Формирование данных для цифровых тренажеров операторов металлургических процессов
https://doi.org/10.17073/0368-0797-2023-2-236-243
Аннотация
В статье рассматриваются вопросы формирования модельных реализаций временных рядов данных (на основе натурных данных) контролируемых и неконтролируемых воздействий в тренажерно-обучающих системах и системах цифрового моделирования. Такие тренажеры получают все более широкое распространение в связи с развитием информационных и компьютерных технологий, автоматизированных систем научных исследований, обучающих систем, технологий цифрового моделирования (АПМ-моделирования), а также цифровых двойников и систем усовершенствованного управления. Сформированные реализации воздействий могут характеризовать ситуации нормального протекания процесса, аварийных и предаварийных состояний, или специфичные типопредставительные ситуации для обучения операторов и технологического персонала, тестирования программного обеспечения, исследования и настройки алгоритмов и поиска оптимальных управляющих воздействий. На примерах из металлургической отрасли показана возможность формирования нескольких взаимосвязанных воздействий на основе моделей нелинейной динамики и многовариантных динамических баз данных. В качестве модели формирования воздействий рассматривается система Лоренца, описывающая тепловую конвекцию текучей среды. Параметры модели для низкочастотной и высокочастотной составляющих определяются отдельно, путем обработки натурных данных. Далее формируется учебная выборка с помощью операций нормализации и релейно-экспоненциального сглаживания. Реализации воздействий формируются с учетом взаимной корреляции данных на основе моделей хаотической динамики и подстраиваются до заданных свойств на ограниченной выборке заданного объема с требуемой точностью при помощи генератора в виде замкнутой динамической системы. Генератор в виде замкнутой динамической системы строится на основе многомерной формирующей авторегрессионной модели с подстраиваемыми коэффициентами. Показан пример формирования рядов данных технологических параметров доменной печи (степень износа кладки печи, показания датчиков температуры и плотность теплового потока).
Ключевые слова
Для цитирования:
Ляховец М.В., Макаров Г.В., Саламатин А.С. Формирование данных для цифровых тренажеров операторов металлургических процессов. Известия высших учебных заведений. Черная Металлургия. 2023;66(2):236-243. https://doi.org/10.17073/0368-0797-2023-2-236-243
For citation:
Lyakhovets M.V., Makarov G.V., Salamatin A.S. Data generation for digital simulators of metallurgical process operators. Izvestiya. Ferrous Metallurgy. 2023;66(2):236-243. (In Russ.) https://doi.org/10.17073/0368-0797-2023-2-236-243
Введение
Последние десятилетия с развитием информационных и компьютерных технологий отмечены широким распространением как автоматизированных систем научных исследований, так и автоматизированных обучающих систем компьютерного тренинга [1 – 3]. Успешное использование такого рода систем обусловлено эффективными решениями задач хранения и использования информации, характеризующей функционирование промышленных (натурных) объектов в различных режимах. На текущий момент информационные технологии позволяют решить задачи посредством использования автоматизированных информационных систем, которые включают специализированные базы данных, реализующие хранение информации в виде реляционных моделей данных, и созданы с использованием клиент-серверной архитектуры, позволяющей разнести в пространстве поставщиков и потребителей информации на большие расстояния (вплоть до межконтинентальных). Используя удаленные базы данных, можно аккумулировать натурные значения, описывающие функционирование разнообразных подобных натурных объектов, собираемые как традиционными средствами, так и средствами Индустрии 4.0 [4].
Безусловно, при решении исследовательских и образовательных задач невозможно проводить интенсивное обучение и тренинг (не только при отработке навыков действия операторов в аварийных и нештатных ситуациях), а также проводить экспериментальную апробацию научных гипотез непосредственно на рабочих местах. Таким образом, необходимо использовать модельные представления реальных установок, которые должны быть территориально независимы от натурных объектов. Для моделирования физических процессов, прочностного расчета и проектирования конструкций, деталей машин и механизмов хорошо себя зарекомендовал подход APM-моделирования (Analysis Process Model) [5]. Решение указанных задач в системах управления требует подхода с акцентом не только на физику процесса, но и на требуемые характеристики этих процессов с точки зрения управления. При этом необходимо наличие многих однотипных вариантов реализации натурных данных, которые не всегда имеет смысл хранить, или необходимо практически бесконечное число вариантов статистически подобных реализаций. Таким образом, встает вопрос о формировании модельных реализаций на базе натурных рядов данных, причем на многовариантной основе [6].
В настоящей работе рассмотрен вариант решения задачи создания инструмента для получения псевдослучайных последовательностей с заданными характеристиками на основе многовариантных имитаторов. В работе [7] рассматривается подход к решению такой задачи при помощи многовариантных динамических баз данных, позволяющих производить варианты реализаций модельных данных, близких по статистическим и динамическим характеристикам к данным, отражающим функционирование натурных объектов управления, на основе типопредставительных реализаций натурных данных. В настоящей работе, в отличие от работы [7], рассматривается способ формирования генератора случайных последовательностей, в котором многовариантные динамические базы данных заменены на классическую модель нелинейной динамики и многовариантный фильтр релейно-экспоненциального сглаживания. Применение такого подхода позволит увеличить разнообразие вариантообразующих процедур с вариантностью по воздействиям, условиям и преобразованиям.
Модели хаотической динамики
Для формирования случайных реализаций временных рядов предлагается использовать модели хаотической динамики с раздельной имитацией колебательной (низкочастотной) и нестационарной (высокочастотной) компонент ряда. Прототипами послужили методы, представленные в работах [8; 9]. Рассмотрим способ многовариантного формирования модельных реализаций на базе натурных рядов данных с помощью модели тепловой конвекции в атмосфере, предложенной Лоренцем. Способ применения многовариантного имитатора покажем на примере имитации теплового состояния фурменной зоны доменной печи.
Система (аттрактор) Лоренца, используемая для описания тепловой конвекции в атмосфере, может быть представлена в следующем виде [10; 11]:
| \[\left\{ \begin{array}{l}\dot X = \sigma (Y - X);\\\dot Y = pX - Y - XZ;\\\dot Z = - \beta Z + XY.\end{array} \right.\] | (1) |
где σ, р, β – коэффициенты аттрактора Лоренца; X, Y, Z – формируемые ряды.
С помощью системы уравнений (1) можно рассчитать, как будет вести себя текучая среда, которую равномерно разогревают снизу и охлаждают сверху (воздушные потоки в атмосфере). В частности, она позволяет понять, к какому результату приведет даже небольшое изменение исходных параметров.
Модельные реализации технологического режима формируются с помощью предлагаемого в настоящей работе метода в три этапа:
– имитация низкочастотной составляющей;
– имитация высокочастотной составляющей;
– многоитерационная корректировка реализаций для достижения заданной точности воспроизведения их свойств.
Формирование низкочастотной составляющей
Низкочастотная составляющая представляет собой тренд, формирующийся с помощью последовательной настройки коэффициентов σ, р, β аттрактора Лоренца по отклонениям модельных данных от натурных на предыдущем шаге имитации. Имитация осуществляется по следующему алгоритму.
1 этап. Выбор исходных реализаций натурных данных.
На этом этапе выбираются три ряда натурных данных по условию высокой степени взаимной корреляции (желательно, чтобы выбранные ряды несли типопредставительный характер изменения технологических параметров – степень износа кладки печи (\({X^N}(l)\)); показания датчиков температуры (\({Y^N}(l)\)); плотность теплового потока (\({Z^N}(l)\))).
2 этап. Нормализация.
Выбранные на предыдущем этапе ряды данных подлежат нормализации, например, по формулам из работы [12].
3 этап. Сглаживание рядов данных.
Проводится обработка выбранных нормализованных рядов данных X(l), Y(l), Z(l) с помощью релейно-экспоненциального сглаживателя первого порядка [13]:
\[\begin{array}{c}\tilde X(l) = \tilde X(l - 1) + \\ + \alpha \left\{ \begin{array}{l}X(l) - \tilde X(l - 1),{\rm{при}}\left| {X(l) - \tilde X(l)} \right| \le \beta ;\\\beta sign\left[ {X(l) - \tilde X(l - 1)} \right],{\rm{при}}\left| {X(l) - \tilde X(l)} \right| > \beta .{\rm{ }}\end{array} \right.\end{array}\]
где \(\tilde X\)(l) – сглаженное значение; l – дискретное время; βsign – коэффициент β с нужным знаком.
Настроечный параметр (β > 0) определяется следующим образом:
\[\beta = \left| {{\Delta ^s}} \right| + (2 \div 3){\sigma _N},X\]
где \(\left| {{\Delta ^s}} \right|\) – модуль вероятного приращения полезного сигнала на соседних отсчетах; σN – среднеквадратическое отклонение обычной (без учета грубых выбросов) помехи с нормальным распределением и нулевым средним.
Настроечный коэффициент α выбирается из диапазона [0; 1] для достижения чувствительности и сглаживания в соответствии с динамикой исследуемого процесса.
4 этап. Формирование учебной выборки.
Из полученных рядов формируется учебная выборка для расчета коэффициентов системы Лоренца (σ, р, β) на каждый отсчет. Принимая во внимание, что производную можно определить через разность между соседними отсчетами (при интервале дискретизации, равным 1), получим
| \[\begin{array}{c}\dot X = \tilde X(l) - \tilde X(l - 1);{\rm{ }}\\\dot Y = \tilde Y(l) - \tilde Y(l - 1);{\rm{ }}\\\dot Z = \tilde Z(l) - \tilde Z(l - 1).\end{array}\] | (2) |
Подставляем в систему Лоренца (1) полученные выражения (2):
| \[\begin{array}{c}{{\tilde X}^{\rm{н}}}(l) - {{\tilde X}^{\rm{н}}}(l - 1) = \sigma (l - 1)\left[ {{{\tilde Y}^{\rm{н}}}(l - 1) - {{\tilde X}^{\rm{н}}}(l - 1)} \right];{\rm{ }}\\{{\tilde Y}^{\rm{н}}}(l) - {{\tilde Y}^{\rm{н}}}(l - 1) = p(l - 1){{\tilde X}^{\rm{н}}}(l - 1) - {{\tilde Y}^{\rm{н}}}(l - 1) - {{\tilde X}^{\rm{н}}}(l - 1){{\tilde Z}^{\rm{н}}}(l - 1);{\rm{ }}\\\tilde Z(l) - \tilde Z(l - 1) = - \beta (l - 1){{\tilde Z}^{\rm{н}}}(l - 1) + {{\tilde X}^{\rm{н}}}(l - 1){{\tilde Y}^{\rm{н}}}(l - 1).\end{array}\] | (3) |
Из уравнений (3) выражаем коэффициенты σ, р, β:
| \[\begin{array}{c}\sigma (l - 1) = \frac{{{{\tilde X}^{\rm{н}}}(l) - {{\tilde X}^{\rm{н}}}(l - 1)}}{{{{\tilde Y}^{\rm{н}}}(l - 1) - {{\tilde X}^{\rm{н}}}(l - 1)}};\\p(l - 1) = \frac{{{{\tilde Y}^{\rm{н}}}(l - 1) + {{\tilde X}^{\rm{н}}}(l - 1){{\tilde Z}^{\rm{н}}}(l - 1)}}{{{{\tilde X}^{\rm{н}}}(l - 1)}};\\\beta (l - 1) = \frac{{{{\tilde X}^{\rm{н}}}(l - 1){{\tilde Y}^{\rm{н}}}(l - 1) - \tilde Z(l) + \tilde Z(l - 1)}}{{\tilde Z(l - 1)}}.\end{array}\] | (4) |
5 этап. Формирование модельных воздействий.
Для формирования модельных воздействий достаточно задать начальные значения X \(^{\rm{м}}\)(0), Y\(^{\rm{м}}\)(0), Z\(^{\rm{м}}\)(0) и подставить вместе с коэффициентами σ(l), р(l), β(l) в формулы
| \[\begin{array}{c}{X^{\rm{м}}}(l) = {X^{\rm{м}}}(l - 1) + \sigma (l - 1)\left[ {{Y^{\rm{м}}}(l - 1) - {X^{\rm{м}}}(l - 1)} \right];\\{Y^{\rm{м}}}(l) = p(l - 1){X^{\rm{м}}}(l - 1) - {X^{\rm{м}}}(l - 1){Z^{\rm{м}}}(l - 1);\\{Z^{\rm{м}}}(l) = {Z^M}(l - 1) - \beta (l - 1){Z^{\rm{м}}}(l - 1) + {Z^{\rm{м}}}(l - 1){Y^{\rm{м}}}(l - 1).\end{array}\] | (5) |
6 этап. Приведение данных к исходному диапазону изменения.
Проводится операция, обратная операции нормализации, выполненной на этапе 2:
\[V_i^{\rm{м}}(l) = V_{{\rm{норм}},i}^{\rm{н}}(l)\left( {V_{\max ,i}^{\rm{н}} - V_{\min ,i}^{\rm{н}}} \right) + V_{\min ,i}^{\rm{н}};\]
здесь \(V_{{\rm{норм}},i}^{\rm{н}}\)(l) – модельные воздействия, рассчитанные по формуле (5).
Варьируя настроечными коэффициентами релейно-экспоненциального сглаживания и начальными условиями имитации, получим вариантные оценки модельных воздействий.
Формирование высокочастотной составляющей
Высокочастотная составляющая определяется как разность между фактическим и сглаженным значениями в l-ый момент времени (l = 1, 2, …, N, где N – количество данных). Для нахождения высокочастотной составляющей используется система Лоренца. Алгоритм имитации следующий.
1 этап. Определение отклонений фактических от сглаженных нормализованных значений.
На этом этапе вычисляется разность между фактическим нормализованным и сглаженным нормализованными значениями в l-ый момент времени:
| \[\begin{array}{c}\Delta {X^{\rm{н}}}(l) = {X^{\rm{н}}}(l) - \tilde X(l);\\\Delta {Y^{\rm{н}}}(l) = {Y^{\rm{н}}}(l) - \tilde Y(l);\\\Delta {Z^{\rm{н}}}(l) = {Z^{\rm{н}}}(l) - \tilde Z(l).\end{array}\] | (6) |
2 этап. Формирование учебной выборки.
Из полученных рядов формируется учебная выборка для расчета коэффициентов системы Лоренца (Δσ, Δр, Δβ) на каждый отсчет. Принимая во внимание, что производную можно определить через разность между соседними отсчетами (при интервале дискретизации 1), выражаем коэффициенты Δσ, Δр, Δβ в приращениях сигнала:
| \[\begin{array}{c}\sigma (l - 1) = \frac{{\Delta {X^{\rm{н}}}(l) - \Delta {X^{\rm{н}}}(l - 1)}}{{\Delta {Y^{\rm{н}}}(l - 1) - \Delta {X^{\rm{н}}}(l - 1)}};\\p(l - 1) = \frac{{{{\tilde Y}^{\rm{н}}}(l - 1) + {{\tilde X}^{\rm{н}}}(l - 1){{\tilde Z}^{\rm{н}}}(l - 1)}}{{{{\tilde X}^{\rm{н}}}(l - 1)}};\\\beta (l - 1) = \frac{{{{\tilde X}^{\rm{н}}}(l - 1){{\tilde Y}^{\rm{н}}}(l - 1) - \tilde Z(l) + \tilde Z(l - 1)}}{{\tilde Z(l - 1)}}.\end{array}\] | (7) |
3 этап. Формирование модельной высокочастотной составляющей.
Для формирования модельной высокочастотной составляющей достаточно задать начальные значения X \(^{\rm{м}}\)(0), Y\(^{\rm{м}}\)(0), Z\(^{\rm{м}}\)(0) и подставить вместе с коэффициентами (Δσ, Δр, Δβ) в формулы:
| \[\begin{array}{c}\Delta {X^{\rm{м}}}(l) = \Delta {X^{\rm{м}}}(l - 1) + \Delta \sigma (l - 1)\left[ {\Delta {Y^{\rm{м}}}(l - 1) - \Delta {X^{\rm{м}}}(l - 1)} \right];\\\Delta {Y^{\rm{м}}}(l) = \Delta p(l - 1)\Delta {X^{\rm{м}}}(l - 1) - \Delta {X^{\rm{м}}}(l - 1)\Delta {Z^{\rm{м}}}(l - 1);\\{Z^{\rm{м}}}(l) = \Delta {Z^{\rm{м}}}(l - 1) - \Delta \beta (l - 1)\Delta {Z^{\rm{м}}}(l - 1) + \Delta {Z^{\rm{м}}}(l - 1)\Delta {Y^{\rm{м}}}(l - 1).\end{array}\] | (8) |
4 этап. Формирование модельных воздействий:
| \[\begin{array}{c}{X^{\rm{м}}}(l) = X_{\rm{н}}^{\rm{м}}(l) + \Delta {X^{\rm{м}}}(l);\\{Y^{\rm{м}}}(l) = Y_{\rm{н}}^{\rm{м}}(l) + \Delta {Y^{\rm{м}}}(l);\\{Z^{\rm{м}}}(l) = Z_{\rm{н}}^{\rm{м}}(l) + \Delta {Z^{\rm{м}}}(l),\end{array}\] | (9) |
где \(X_{\rm{н}}^{\rm{м}}(l)\), \(Y_{\rm{н}}^{\rm{м}}(l)\), \(Z_{\rm{н}}^{\rm{м}}(l)\) – низкочастотная составляющая модельного воздействия.
5 этап. Приведение данных к исходному диапазону изменения.
Проводится операция, обратная операции нормализации:
\[V_i^{\rm{м}}(l) = V_{{\rm{норм}},i}^{\rm{м}}(l)\left( {V_{\max ,i}^{\rm{н}} - V_{\min ,i}^{\rm{н}}} \right) + V_{\min ,i}^{\rm{н}};\]
здесь \(V_{{\rm{норм}},i}^{\rm{м}}\)(l) – модельные воздействия, рассчитанные по формуле (9).
Подстройка корреляционной функции
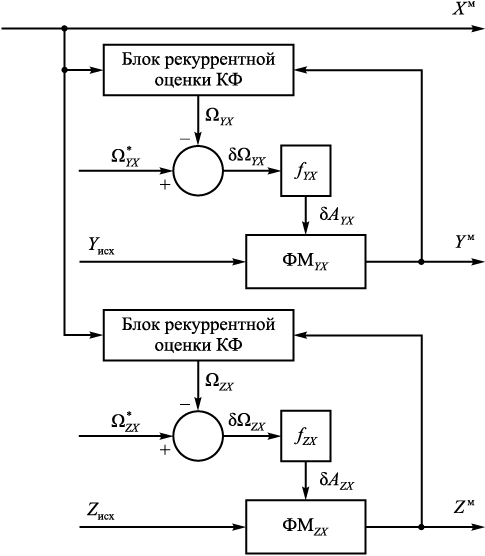
При использовании изложенной выше последовательности действий формируются ряды с достаточно высокой степенью корреляции, однако конкретные значения корреляционной функции (КФ) могут отличаться от исходных натурных данных. Поэтому достичь воспроизводимости характеристик при численном моделировании возможно только при значительных объемах моделируемой выборки (сотни тысяч моделируемых точек). Хотя современные вычислительные системы позволяют это сделать [14; 15], производственные задачи требуют обеспечить заданные свойства воздействий на коротких участках данных (тысячах или даже всего сотнях отсчетов). Для решения такой задачи при формировании одной переменной [7] был разработан алгоритм формирования сигналов с заданными свойствами, одним из которых является автокорреляционная функция. Вариант такого алгоритма для нескольких связанных переменных с заданной корреляционной функцией представлен на рис. 1.
Рис. 1. Схема генератора в виде замкнутой динамической системы |
Представленный генератор позволяет формировать ряды данных Y\(^{\rm{м}}\), Z\(^{\rm{м}}\) с заданной корреляционной функцией с рядом X\(^{\rm{м}}\), полученным описанным выше методом или в виде значений физического (или натурного) сигнала из АСУ ТП, характеризующегося динамическими свойствами ΩYX (ΩZX ), оцениваемыми в блоке рекуррентной оценки КФ, которые учитываются в блоке прямой цепи. Блок обратной связи позволяет оперативно корректировать параметры формирующей модели (ФМ) δAYX (δAZX ) по отклонению свойств итогового сигнала ΩYX (ΩZX ) от заданных \(\Omega _{YX}^*\)(\(\Omega _{ZX}^*\)).
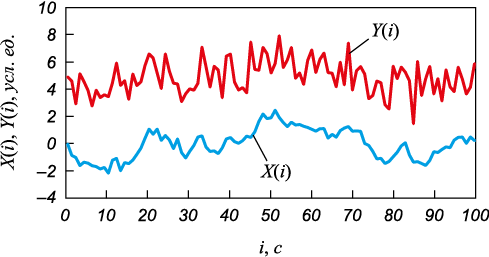
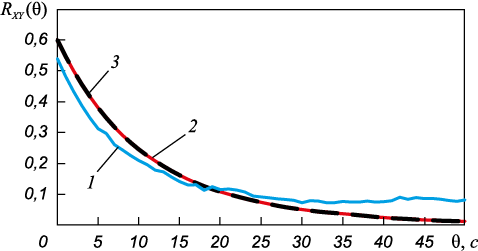
На рис. 2 представлен фрагмент коррелированных сигналов X(l) и Y(l), а на рис. 3 – графики корреляционных функций. Корреляция сигналов, сформированных с помощью модели первого порядка, на ограниченном интервале не дает достичь заданной точности. На рис. 3 видно, что исходная корреляционная функция сигналов X(l) и Y(l) имеет отклонение значений от заданных более 5 % при моделируемой выборке 25 000 отсчетов (чем меньше интервал, тем больше отклонения).
Рис. 2. Фрагмент коррелированных сигналов
Рис. 3. Корреляционные функции сигналов: |
Представлены корреляционные функции исходных сигналов, заданная корреляционная функция и полученная после генератора корреляционная функция для формируемых сигналов. После процедуры подстройки в генераторе отклонения заданной и фактической корреляционной функции составили менее 1 %.
Для достижения заданной точности воспроизведения свойств применяется многоитерационная процедура подстройки с помощью генератора (рис. 1). Формирующая модель (ФМ) для сигнала Y\(^{\rm{м}}\) представлена в следующем виде:
| \[V_i^{\rm{м}}(l) = V_{{\rm{норм}},i}^{\rm{м}}(l)\left( {V_{\max ,i}^{\rm{н}} - V_{\min ,i}^{\rm{н}}} \right) + V_{\min ,i}^{\rm{н}};\] | (10) |
где n – порядок формирующей модели.
Корректировка коэффициентов \(\tilde \alpha \)XY( j) проводится по следующей формуле
| \[{\tilde \alpha _{XY}}(j) = \Delta {A_{XY}} + {\alpha _{XY}}(j),\] | (11) |
где αXY( j) – текущий коэффициент авторегрессии; \(\tilde \alpha \)XY( j) – скорректированный коэффициент авторегрессии; ΔAXY – отклонение от заданного значения КФ на выходе после оператора обратной связи fXY .
При невозможности достичь заданной точности воспроизведения при текущем порядке формирующей модели (10) проводится повышение порядка n + 1 и процедура (11) повторяется до тех пор, пока не будет достигнута заданная точность.
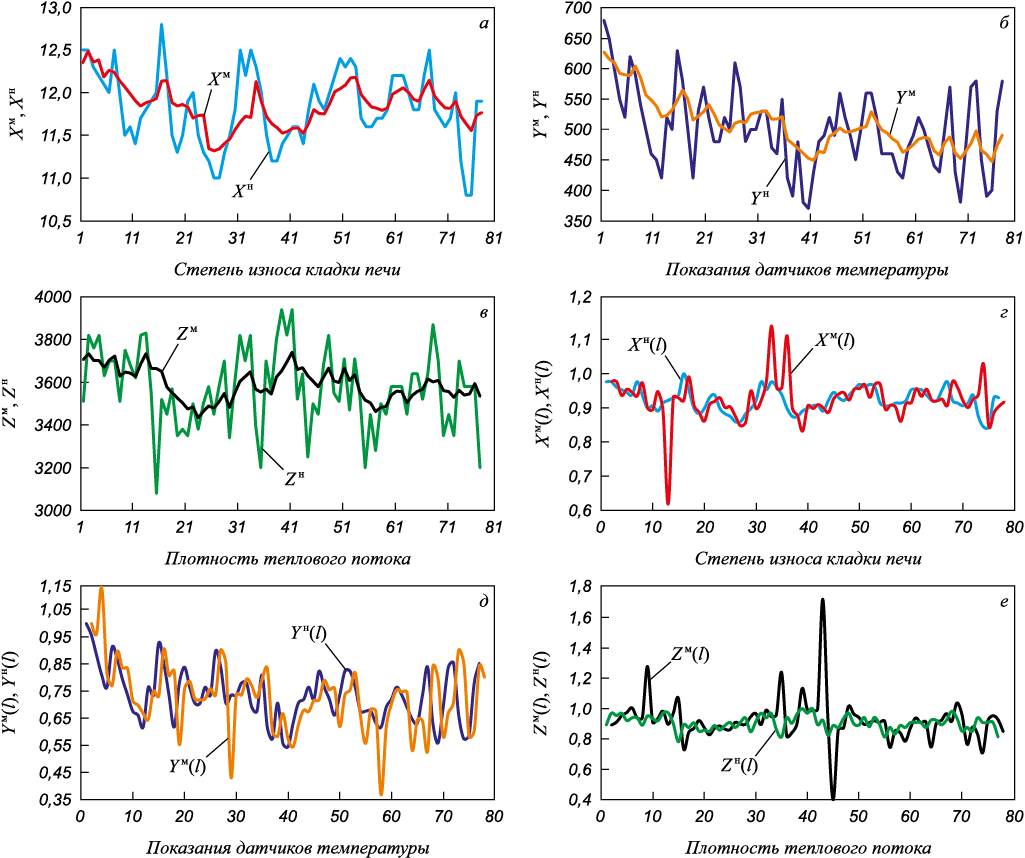
В соответствии с вышеописанным алгоритмом было реализовано численное моделирование (рис. 4). Анализируя результаты моделирования, можно сделать следующие выводы. Имитация по первому каналу дает хорошие результаты. Во втором варианте есть одиночные выбросы (это объясняется малыми приращениями, которые используются для вычисления параметров модели Лоренца). В целом эта модель достаточно точно (в пределах исследовательской точности) отслеживает динамику сигнала и сохраняет заданные значения свойств.
Рис. 4. Результаты имитации по первому (а, б, в) и второму каналам (г, д, е): |
Сформированные последовательности могут быть использованы как в тренажерно-обучающих системах, так и при проектировании и настройке алгоритмов оценивания и контроля различных производственных ситуаций, когда влияние одной величины на другие подчиняется определенным зависимостям, но построение моделей затруднено. Например, для формирования обучающих и тестовых выборок для алгоритмов и подсистем мониторинга и предотвращения предаварийных и аварийных ситуаций [16]. Другими примерами для применения предложенных решений могут служить многоточечные измерительные системы [17], цифровые двойники, описанные в работе [18] в соответствии с ГОСТ Р 57700.37 – 2021 [19], при построении и исследовании комплексных моделей [20], и другие модели и моделирующие комплексы, применяемые при моделировании сложных систем [21; 22].
Выводы
Отдельным применением предложенной схемы формирования воздействий можно выделить задачи математического моделирования и алгоритмизации функций мониторинга технологических процессов на основе многоточечных измерительных систем, в которых при построении моделей выполнен учет технологических параметров, влияющих на качество реализации главной функции объекта управления и требующих измерения и контроля, включая концентрацию веществ и взвешенных частиц, между которыми установлены функциональные зависимости, после чего применяется мультиверсионный подход для получения N-го количества измеряемых данных. Рассматриваемый подход можно дополнить с помощью предложенного в настоящей работе алгоритма моделирования, использовав натурные данные или модельные реализации для его настройки. Это позволит дать множество альтернативных реализаций вариантов протекания одного процесса с заданными свойствами зависимостей между параметрами для более точной дальнейшей настройки и исследования алгоритмов и систем.
Предложенный двухэтапный алгоритм формирования данных предлагается включать в структуру цифровых двойников, соответствующих ГОСТ Р 57700.37 – 2021, который устанавливает следующее определение: объединяя различные математические модели и методы имитационного моделирования в единую систему, можно получить новую сущность – цифровой двойник, который позволяет всесторонне описать изделие и системно подойти к разработке, производству и эксплуатации изделий. Для эффективного применения рассмотренного алгоритма в системе цифрового двойника должны быть предусмотрены связи с моделями типопредставительных ситуаций, логических состояний вход/выходных сигналов технологического оборудования и цепей управления им, пересчетными, статистическими, конструкторскими, APM-моделями и другими моделями, описывающими процесс с необходимых сторон.
Список литературы
1. Beloglazov I.I., Petrov P.A., Bazhin V.Y. The concept of digital twins for tech operator training simulator design for mining and processing industry. Eurasian Mining. 2020;(2): 50–54. https://doi.org/10.17580/em.2020.02.12
2. Ackers D. Stations AR simulated digital twin. In: XR Case Studies. Management for Professionals. Springer, Cham; 2021:83–90. https://doi.org/10.1007/978-3-030-72781-9_11
3. Zinchenko S., Mateichuk V, Nosov P., Popovych I., Solovey O., Mamenko P., Grosheva O. Use of simulator equipment for the development and testing of vessel control systems. Electrical, Control and Communication Engineering. 2021;16(2):58–64. https://doi.org/10.2478/ecce-2020-0009
4. Спирин Н.А., Рыболовлев В.Ю., Лавров В.В., Гурин И.А., Шнайдер Д.А., Краснобаев А.В. Научные проблемы создания интеллектуальных систем управления технологическими процессами в пирометаллургии на основе концепции “индустрия 4.0”. Металлург. 2020;(6):71–76.
5. Kuzlyakina V.V. Integration processes in engineering education. In: New Trends in Educational Activity in the Field of Mechanism and Machine Theory. Springer, Cham; 2014: 47–55.
6. Авдеев В.П., Кустов Б.А., Мышляев Л.П. Производственно-исследовательские системы с многовариантной структурой. Новокузнецк: изд. Кузбасского филиала Инженерной академии; 1992:188.
7. Ляховец М.В., Макаров Г.В., Саламатин А.С. Моделирование возмущений при исследовании управляющих систем. Вестник Астраханского государственного технического университета. Серия: Управление, вычислительная техника и информатика. 2020;4:70–79.
8. Nagiev F.B. The Lorentz system and the prediction of yield of petroliferous strata. Automation and Remote Control. 1998;9(9):182–186.
9. Сонечкина Д.М. и др. Новый способ экстраполяции хаотических временных рядов посредством Вейвлетов с приложением их к динамике климата. Известия вузов. Прикладная нелинейная динамика. 1996;4(4-5).
10. Pchelintsev A.N. Numerical and physical modeling of the dynamics of the Lorenz system. Numerical Analysis and Applications. 2014;7(2):159–167. https://doi.org/10.1134/S1995423914020098
11. Gorman M., Widmann P.J., Robbins K.A. Nonlinear dynamics of a convection loop: A quantitative comparison of experiment with theory. Physica D. 1986;19(2):255–267. https://doi.org/10.1016/0167-2789(86)90022-9
12. Рыков А.С. Методы системного анализа: оптимизация. Москва: НПО Изд-во экономика; 1999:255.
13. Даниелян Т.М., Авдеев В.П., Парпаров Я.Г. Первичная обработка информации с помощью ЭВМ. Известия вузов. Черная металлургия. 1981;24(7):14–19.
14. Soucek B., Prohorov S. Event – train correlation and real – time microcomputer systems. Microprocessing and Microprogramming. 1983;11(1):23–29.
15. Tsoukalas I., Kossieris P., Makropoulos C. Simulation of non-Gaussian correlated random variables, stochastic processes and random fields: Introducing the anySim R-package for environmental applications and beyond. Water. 2020; 12(6):1645. https://doi.org/10.3390/w12061645
16. Ляховец М.В., Макаров Г.В., Саламатин А.С., Шипунов М.В. Оценивание предаварийных состояний технологического оборудования и контрольно-измерительных приборов. Промышленные АСУ и контроллеры. 2020;(3): 16–24.
17. Ковалев И.В., Ковалев Д.И., Лосев В.В., Сарамуд М.В., Тынченко Я.А. Математическое моделирование и алгоритмизация функций мониторинга технологических процессов на основе многоточечных измерительных систем. Современные наукоемкие технологии. 2021;(6-1): 29–38.
18. Скударнова Н.В., Макаров Г.В., Свинцов М.М. Программная реализация модели тяжелосредного гидроциклона как компонента цифрового двойника производства. В кн.: Системы автоматизации в образовании, науке и производстве. AS’2021. Труды XIII Всероссийской научно-практической конференции (с международным участием). Новокузнецк: ИЦ СибГИУ; 2021:151–155.
19. ГОСТ Р 57700.37 – 2021. Компьютерные модели и моделирование. Цифровые двойники изделий. Общие положения. Москва: ИПК Изд-во стандартов; 2021:10.
20. Makarov G.V., Tamarkina E.V., Lyakhovets M.V., Salamatin A.S. Functional status technological equipments modelling. IOP Conference Series: Materials Science and Engineering. 2020;865(1):012010. https://doi.org/10.1088/1757-899X/865/1/012010
21. Советов Б.Я., Яковлев С.А. Моделирование систем. Москва: Изд-во Юрайт; 2019:343.
22. Бусленко Н.П. Моделирование сложных систем. Москва: Наука; 1978:400.
Об авторах
М. В. ЛяховецРоссия
Михаил Васильевич Ляховец, к.т.н., доцент кафедры автоматизации и информационных систем
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Г. В. Макаров
Россия
Георгий Валентинович Макаров, старший преподаватель кафедры менеджмента качества и инноваций
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
А. С. Саламатин
Россия
Александр Сергеевич Саламатин, ассистент кафедры автоматизации и информационных систем
Россия, 654007, Кемеровская обл. – Кузбасс, Новокузнецк, ул. Кирова, 42
Рецензия
Для цитирования:
Ляховец М.В., Макаров Г.В., Саламатин А.С. Формирование данных для цифровых тренажеров операторов металлургических процессов. Известия высших учебных заведений. Черная Металлургия. 2023;66(2):236-243. https://doi.org/10.17073/0368-0797-2023-2-236-243
For citation:
Lyakhovets M.V., Makarov G.V., Salamatin A.S. Data generation for digital simulators of metallurgical process operators. Izvestiya. Ferrous Metallurgy. 2023;66(2):236-243. (In Russ.) https://doi.org/10.17073/0368-0797-2023-2-236-243
JATS XML