Параметры субструктуры в деформированных сплавах Cu – Mn с ГЦК решеткой

Введение

Варьирование состава сплавов системы Cu – Mn может менять степень ближнего порядка и сопротивление движению дислокаций [1, 2]. В то же время в сплавах этой системы значение энергии дефекта упаковки (ЭДУ) незначительно зависит от концентрации легирую­щего компонента – марганца [3]. Варьирование концентрации второго элемента в твердом растворе может приводить к изменению напряжения старта дислокаций и сил трения и, следовательно, к изменению сопротивления началу пластической деформации. Увеличение степени деформации приводит к формированию определенного типа дислокационной субструктуры, которая, в свою очередь, определяет деформационное упрочнение поликристаллов. Характер и тип образующихся дислокацион­ных структур тесно связаны с величиной ЭДУ, параметрами локального порядка и силами трения между дислокациями. Эти параметры могут сильно изменяться в зависимости от концентрации легирующего элемента, от степени упорядочения в твердых раст­ворах, а также от степени деформации [4 – 6].

Много лет дислокационную структуру характеризовали, в основном, таким параметром, как средняя скалярная плотность дислокаций <ρ>. Дальнейшее развитие исследований дислокаций привело к разделению величины <ρ> на разные по физическому смыслу компоненты: геометрически необходимые ρ_G и статисти­чески запасенные ρ_S дислокации. В литературе показано, что геометрически необходимые дислокации образуются при деформации в поликристаллических металлах и сплавах с деформационными двойниками, в дисперсно-упрочненных материалах и в других случаях функционирования прочных барьеров дислокацион­ному скольжению [7 – 9].

Плотность ρ_G связана непосредственно с кривизной-кручением кристаллической решетки χ [13, 14]:

\[{\rho _G} = \frac{1}{b}\frac{{\partial \varphi }}{{\partial \ell }} = \frac{\chi }{b} = {(rb)^{ - 1}},\]

где b – вектор Бюргерса; φ – угол наклона кристаллографической плоскости; ℓ – расстояние на плоскости; \(\chi  = \large\frac{{\partial \varphi}}{{\partial \ell}}\) – кривизна-кручение кристаллической решетки; r – радиус кривизны кристалла.

Образование дислокаций и дислокационные реакции в сплавах после пластической деформации можно считать случайными процессами. Подвергнутые торможению одни дислокации другими, которые образовались в процессе пластической деформации, называются статистически запасенными (СЗД) [11]. Такие статистически запасенные дислокации образуются в самом начале пластической деформации и тормозятся, в основном, слабыми барьерами, состоящими из других дислокаций. В случае присутствия в сплавах более прочных барьеров (таких, как частицы вторых фаз, деформационные двойники или границы зерен) в материале происходит накопление геометрически необходимых дислокаций (ГНД), при этом имеют место градиенты пластической деформации (1) [11]. В результате средняя скалярная плотность дислокаций определяется выражением

<ρ> = ρ_S + ρ_G.

В настоящей работе методом просвечивающей электронной микроскопии изучено влияние легирования марганцем и размера зерен в деформированных сплавах Cu – Mn с ГЦК решеткой.

Материал и методы исследования

Материалами исследования являлись поликристаллические сплавы системы Cu – Mn в интервале концентраций марганца от 0,4 до 25 % (здесь и далее ат.). Исследовали сплавы со средним размером зерен: 10, 20, 40, 60, 100, 120 и 240 мкм. Деформацию образцов исследованных сплавов осуществляли растяжением при комнатной температуре со скоростью 2·10^–2 с^–1. Дислокационную структуру изучали методом просвечивающей дифракционной электронной микроскопии (ПЭМ) на снабженных гониометром электронных микроскопах с ускоряющим напряжением 125 кВ. Просмотр фольг в колонне микроскопа происходил при увеличении 30 000 крат. Методика измерения параметров дислокационной структуры приведена в работах [12, 13].

Результаты исследований и их обсуждение

Рассмотрим формирование дислокационной субструктуры (ДСС) в зависимости от концентрации легирующего элемента при небольших (ε_ист = 0,05) степенях деформации в медно-марганцевых сплавах. Для удобства сравнения субструктур приводятся результаты исследования для одного размера зерен – 100 мкм.

На рис. 1 представлены типы дислокационных субструктур, формирующихся при росте концентрации второго элемента. Анализ электронно-микроскопи­ческих изображений позволил выявить следующие закономерности в формировании ДСС. При умеренных степенях деформации (ε_ист = 0,05 ÷ 0,10) в исследуемых сплавах Cu + 0,4 % Mn, Cu + 8 % Mn и Cu + 19 % Mn происходит образование клубков из дислокаций (рис. 1, а) и ячеистой субструктуры без разориентировок (рис. 1, б). Увеличение концентрации второго компонента до 8 % Mn приводит к переходу от ячеистой к ячеисто-сетчатой ДСС (рис. 1, в). Дальнейший рост концентрации второго элемента сопровождается формированием нового типа ДСС. В сплавах Cu + 13 % Mn, Cu + 19 % Mn и Cu + 25 % Mn наблюдается следующая последовательность формирования типов ДСС: дислокационный хаос (рис. 1, г); дислокационные скопления и петли из дислокаций (рис. 1, д); сетчатая ДСС (рис. 1, е) соответственно.

Рассмотрим влияние роста степени деформации в исследованных сплавах, что приводит к появлению разориентировок в ДСС. На электронно-микроскопических изображениях это проявляется в возникновении экстинкционных деформационных контуров (рис. 2).

В сплавах Cu – Mn с низкой концентрацией легирующего элемента (до 6 %) при степени деформации 0,20 формируется разориентированная ячеистая субструктура (рис. 2, а). В сплавах с концентрацией легирующего элемента выше 8 % Mn при дальнейшем увеличении деформации развивается разориентированная ячеисто-сетчатая субструктура (рис. 2, б). При такой деформации происходит образование сгущений из дислокаций (рис. 2, б), зарождающихся на длинных прямолинейных дислокациях, которые были образованы еще при малых степенях деформации. В результате наблюдается увеличение плотности сгущений и структура стремится к более однородной.

На рис. 2 приведены электронно-микроскопичес­кие изображения типов ДСС, которые формируются при более высоких (ε_ист > 0,20) степенях деформации в сплавах с разной концентрацией легирующего элемента. Экспериментально установлено, что в сплавах с концентрацией второго элемента 0,4, 2, 4 и 6 % Mn наблюдаются следующие субструктуры: разориентированная ячеистая; ячеисто-сетчатая; микрополосовая ДСС. Примеры наблюдаемых типов субструктур для сплава Cu + 0,4 % Mn приведены на рис. 2, а, б. В сплаве Cu + 6 % Mn наблюдается формирование микрополосовой ДСС, которая образуется внутри зерна, формируясь по границам разориентированных ячеек или от границ зерен (рис. 2, в). Важно отметить, что кинетика образования микрополосовой субструктуры и роста ее объемной доли часто связана с прорастанием через сплав оборванных границ.

Было установлено, что в сплавах с более высокой концентрацией легирующего элемента (8, 10, 13, 19 и 25 % Mn) присутствуют такие субструктуры как: разориентированная сетчатая; разориентированная ячеисто-сетчатая ДСС; микрополосовая ДСС. Пример наблюдаемых субструктур при ε_ист > 0,20 представлен на рис. 2, г – е для сплава Cu + 19 % Mn. На основе анализа электронно-микроскопических микрофотографий было установлено, что сплав с 8 Mn % является пограничным при переходе от классически ячеистой ДСС к ячеисто-сетчатой.

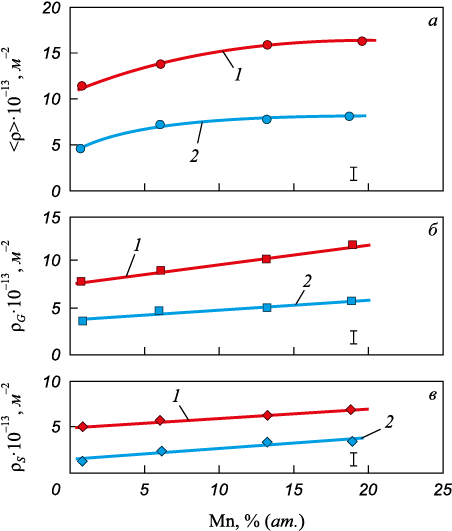
По микрофотографиям были измерены средняя скалярная плотность дислокаций <ρ>, плотность статистически запасенных ρ_S  и геометрически необходимых ρ_G  дислокаций, кривизна-кручение кристаллической решетки χ, плотность микрополос Р_полос., плотность оборванных границ М_об.гр.  при разных размерах зерен <d>. Зависимости средней скалярной плотности дислокаций, плотности геометрически необходимых и статистически запасенных дислокаций от концентрации легирующего элемента С_Mn при ε_ист = 0,30 и размерах зерен 10 и 240 мкм приведены на рис. 3.

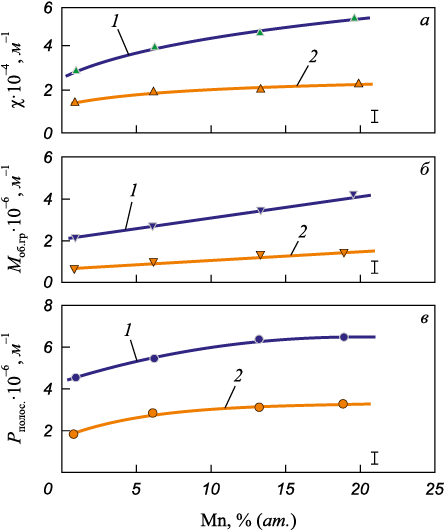
Рост концентрации марганца приводит к увеличению как средней скалярной плотности дислокаций <ρ>, так и ее компонент ρ_G и ρ_S. Рост степени деформации приводит к формированию разориентировок в субструктуре. На рис. 4 приведены зависимости параметров, которые характеризуют разориентировки в сплавах Cu – Mn: кривизна-кручение кристаллической решетки, плотность микрополос и плотность оборванных субграниц. Величины χ, Р_полос. и М_об.гр. возрастают с увеличением концентрации легирующего элемента С_Mn существеннее в сплавах с размером зерен 10 мкм по сравнению со сплавами, в которых размер зерен составляет 240 мкм.

Рассмотрим особенности изменения атомного объе­ма в твердых растворах в сплавах системы Cu – Mn. Считается, что в области существования твердых растворов двух элементов изменение периода решетки в зависимости от состава должно быть линейным. Это предположение было сформулировано в виде закона Вегарда [14 – 16]. Согласно этому закону период решетки твердого раствора из двух компонентов с одинаковой или близкой структурой и периодами а₁ и а₂ должен линейно изменяться в зависимости от концентрации этих компонентов x₁ и x₂ , выраженных в атомных долях:  

а = x₁a₁ + x₂a₂.

С другой стороны, Зен сформулировал правило адди­тивности атомных объемов для идеальных твердых растворов [15 – 17]:

Ω = С_АΩ_А + С_ВΩ_В,

где С_А и С_В, Ω_А и Ω_В – концентрации и атомные объемы чистых компонентов.

Под атомным объемом понимается доля объема элементарной ячейки, приходящаяся на один атом, то есть: 

где n – количество атомов в элементарной ячейке.

Атомные объемы чистых металлов Ω, вычисленные таким образом, менее всего зависят от типа кристаллической решетки. Атомный объем чистых металлов Ω является более универсальной характеристикой относительно параметров элементарных ячеек чистых металлов и может быть использован для анализа свойств соединений, образованных элементами, которые обладают разными кристаллическими структурами. Этот подход был успешно применен в работе [14] при анализе бинарных соединений на основе Ti – Ni.

Закон Зена выполняется так же редко, как и правило Вегарда, но пользуется большой популярностью. Сущест­вует много моделей для предсказания отклонений от закона Зена, но уровень надежности этих предсказаний невелик. Ни одна из моделей даже знак отклонения не предсказывает с точностью более 60 %. Это заставляет думать, что главные факторы, ответственные за отклонение от закона Зена, еще не выявлены.

Для большинства известных сплавов, в которых имеет место образование твердых растворов, наблюдается отрицательное отклонение атомного объема от правила Зена [18, 17]:

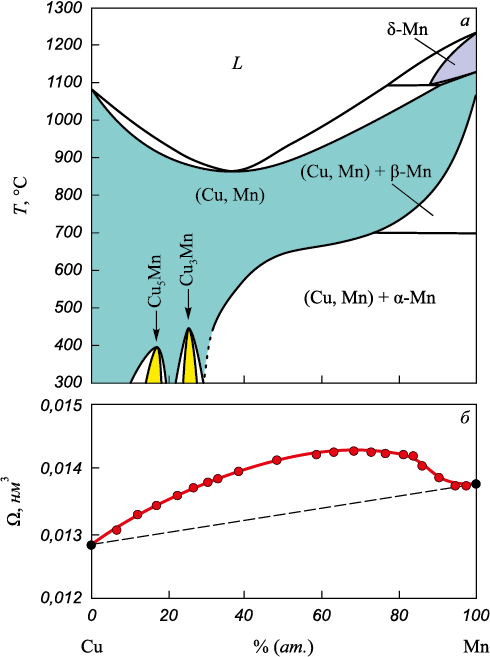
На рис. 5, а приведена фазовая диаграмма системы Cu – Mn, имеющей две концентрационные области, в которых происходит образование упорядоченных фаз в результате фазовых переходов беспорядок – порядок составов Cu₅Mn и Cu₃Mn, а также построены концентрационные зависимости атомных объемов сплавов системы Cu – Mn (рис. 5, б). В сплавах этой системы наблюдается положительное отклонение атомного объе­ма от закона Зена. Такое отклонение от закона Зена на концентрационной зависимости атомного объе­ма встречается значительно реже, чем отрицательное отклонение [20].

Приведенные данные свидетельствуют об изменении сил межатомного взаимодействия при образовании твердых растворов в системе Cu – Mn (согласно выражению, связывающему энергию кристалла с атомным объемом Ω при металлическом характере взаимодействия атомов [21]):

\[U = \frac{{A{e^2}}}{{{\Omega ^{1/3}}}} + \frac{B}{{{\Omega ^{2/3}}}} + \frac{{C{e^2}}}{\Omega };\]

здесь величины \(\large\frac{{A{e^2}}}{{{\Omega ^{1/3}}}}\) и \(\large\frac{B}{{{\Omega ^{2/3}}}}\) представляют собой потенциальную и кинетическую энергии свободных электронов; \(\large\frac{{C{e^2}}}{\Omega }\) характеризует кинетическую энергию электронов, занимающих более низкие энергетические состояния.

Известно, что напряжение Пайерлса Е_п, которое является минимальным необходимым для перемещения дислокации в кристаллических телах напряжением, зависит от межплоскостных расстояний d. При этом максимальное значение Е_п, которое и есть величина барьера Пайерлса, определяется как [22]

\[{\tau _P} = \frac{G}{{1 - \nu}}\exp \left( { - \frac{{2\pi{\omega _{\rm{д}}}}}{b}}\right),\]

здесь \({\omega _{\rm{д}}} = \large\frac{d}{{1 - \nu}}\) – ширина дислокации; d – межплос­костное расстояние; G – модуль сдвига; ν – коэффи­циент Пуассона; b – вектор Бюргерса.

Таким образом, обнаруженная зависимость атомного объема от концентрации для сплавов системы Cu – Mn, согласно приведенному анализу на основе уравнений (1) и (2), позволяет констатировать, что увеличение атомного объема способствует изменению энергии кристалла и высоты барьера Пайерлса. Такие изменения атомного объема оказывают заметное влияние на подвижность статистически запасенных и геометрически необходимых дислокаций.

Выводы

На основе электронно-микроскопических исследований тонкой структуры продеформированных образцов сплавов системы Cu – Mn с ГЦК решеткой определены параметры дислокационных субструктур (средняя скалярная плотность дислокаций <ρ> и ее компоненты: плотность статистически запасенных ρ_S и геометри­чески необходимых ρ_G дислокаций; кривизна-кручение кристаллической решетки χ; плотность микрополос Р_полос. и плотность оборванных субграниц М_об.гр.) в зависимости от концентрации легирующего элемента (марганца) при разных размерах зерен. Определены особенности эволюции дислокационных субструктур в сплавах с разным содержанием марганца и установлено, что сплав с 8 Mn % является пограничным при переходе от классически ячеистой ДСС к ячеисто-сетчатой.

Показано, что уменьшение размера зерен приводит к увеличению параметров дислокационной структуры. Это связано с тем, что в зернах меньшего размера накоп­ление дислокаций связано с их меньшей подвиж­ностью.

На основе анализа концентрационных зависимостей атомных объемов в сплавах в системе Cu – Mn установлено положительное отклонение от закона Зена. Такое увеличение атомного объема с ростом концентрации легирующего элемента способствует изменению энергии кристалла и, как следствие, росту барьера Пайерл­са, и это оказывает заметное влияние на подвижность статистически запасенных и геометрически необходимых дислокаций. Эти данные коррелируют с результатами электронно-микроскопических исследований: в сплавах Cu – Mn с более высоким содержанием марганца наблюдается рост параметров дислокационной субструктуры.

Установлено, что уменьшение размера зерен оказывает более значительное влияние на параметры дислокационной субстуктуры, чем содержание атомов легирующего элемента в сплавах системы Cu – Mn с ГЦК решеткой.